метод. постр. графиков. Методические указания по выполнению расчетнографической работы раздела высшей математики Математический анализ

• Название: Методические указания по выполнению расчетнографической работы раздела высшей математики Математический анализ
• Дата: 30.01.2022
• Размер: 0.54 Mb.
• Имя файла: метод. постр. графиков.doc
• Тип: Методические указания; #346476
• страница: 2 из 3

Асимптоты.


П 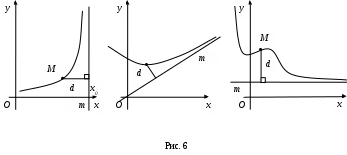рямая линия m называется асимптотой графика функции , если расстояние d от точки M, лежащей на этом графике, до прямой m стремится к нулю при неограниченном удалении этой точки по графику от начала координат в бесконечность (Рис. 6 а), б), в)).

б

в


а

Асимптоты бывают трех видов: вертикальные (рис.6а), наклонные (рис.6б) и горизонтальные (рис.6в).

Прямая называется вертикальной асимптотой графика функции , если хотя бы один из односторонних пределов и равен бесконечности.

Обычно вертикальными асимптотами являются прямые в точках разрыва 2-го рода. Поэтому для отыскания вертикальных асимптот определяют точки бесконечного
разрыва функции. Тогда уравнение вертикальных асимптот . Вертикальные асимптоты могут быть и на границе области определения функции. Например, как у функции .

Прямая называетсянаклонной асимптотой графика функции при (при ), если (соответственно, ).

Уравнение наклонной асимптоты к графику функции ищем виде , где

(*)

и (**)
Если хотя бы один из пределов (*) и (**) не существует или равен бесконечности, то кривая наклонной асимптоты не имеет. Асимптоты графика функции при и могут быть разными. Поэтому при нахождении пределов (*) и (**) следует отдельно рассматривать случай, когда и когда .

Частным случаем наклонной асимптоты (при ) является горизонтальная асимптота.

Прямая является горизонтальной асимптотой графика функции при (при ) тогда и только тогда, когда (соответственно, ).

6. 
   Общая схема исследования функции и построение графиков функций.
   

При построении графика данной функции целесообразно пользоваться следующей схемой:

1. 
   найти область определения функции;
   
2. 
   исследовать функцию на четность, нечетность и периодичность;
   
3. 
   найти точки пересечения графика с осями координат (если это возможно);
   
4. 
   найти интервалы знакопостоянства функции (промежутки, на которых и );
   
5. 
   найти асимптоты;
   
6. 
   найти интервалы возрастания и убывания, экстремумы функции;
   
7. 
   найти интервалы выпуклости и вогнутости, точки перегиба;
   
8. 
   построить график функции.
   

Приведенная схема исследования не является обязательной. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 3, 4, 6. Иногда бывает необходимым вычислить несколько дополнительных точек.

1.7 Примеры выполнения РГР.
Пример 1. Исследовать функцию и построить график .

1. 
   Область определения функции ;
   
2. 
   Исследуем функцию на четность и нечетность: . Получили, и , т.е. данная функция общего вида.
   
3. 
   Находим точки пересечения с осями координат:
   

при ,

при 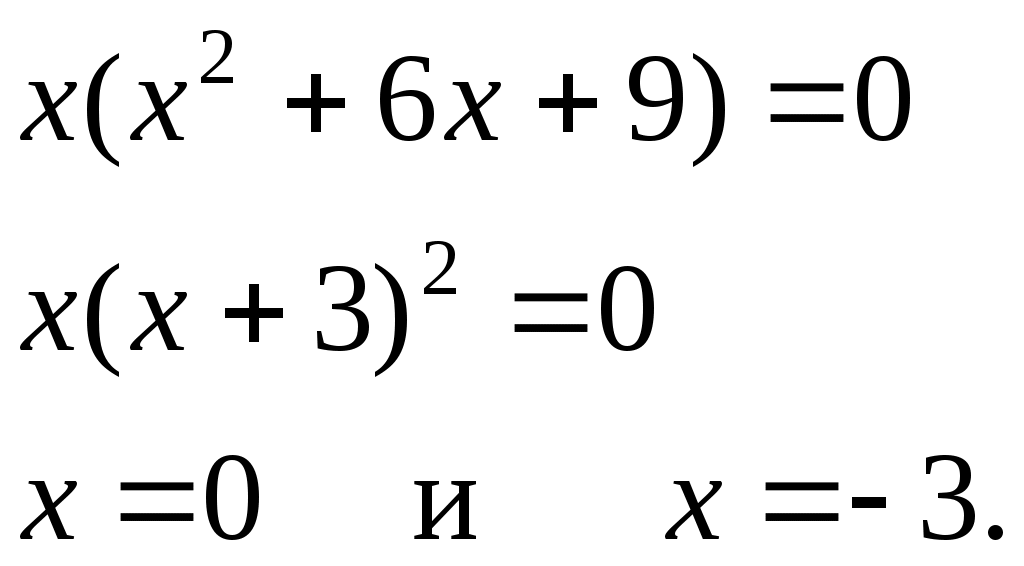решаем уравнение



Точки пересечения (0; 0) и (-3; 0).

4. 
   Найдем интервалы возрастания и убывания функции, экстремумы. Для этого найдем производную и решим уравнение .
   

Производная обращается в ноль при или .

Критические точки

Для проверки достаточных условий экстремума и определения интервалов убывания, возрастания составим таблицу. Полезно нанести критические точки на числовую ось.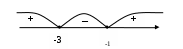

	+	0		0	+
	Возрастает	0 max	У бывает	-4 min	Возрастает

Производная сохраняет знак в каждом из указанных интервалов. Для его определения выберем в каждом интервале пробную точку и определим знак производной в этой точке. Например, в первом интервале выберем точку . Вычислим

, производная больше нуля, функция на этом интервале возрастает и т.д. При переходе через точку производная меняет знак с «плюса» на «минус», следовательно, точка (-3; 0) точка максимума; (-1;-4) - точка минимума.

5. 
   Найдем точки перегиба графика функции. Для этого определим вторую производную и решим уравнение .
   

- критическая точка. Для проверки достаточных условий выпуклости, вогнутости составим таблицу.

		0	+
	Выпуклая	-2 Точка перегиба	Вогнутая

На интервале вторая производная имеет отрицательный знак – график функции на этом интервале выпуклый, на интервале вторая производная положительная – график функции на этом интервале вогнутый, точка (-2; -2) - точка перегиба.

6. 
   Строим график функции (рис. 7). Находим дополнительные точки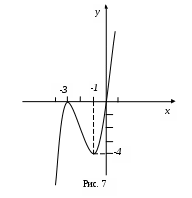
   

Пример 2. Исследовать функцию и построить график .

1. 
   Область определения , т.е. .
   
2. 
   Функция нечетная .
   
3. 
   Точка пересечения с осями (0; 0).
   
4. 
   Интервалы знакопостоянства. Разложим знаменатель на множители 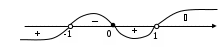. На числовой прямой изобразим точки и определим знак функции в каждом из полученных интервалов.
   

На интервалах и функция имеет положительный знак, на интервалах и - отрицательный.

5. 
   Находим асимптоты. Точки с абсциссами являются точками разрыва, следовательно, вертикальные асимптоты прямые . Определим односторонние пределы в этих точках.
   

Наклонную асимптоту будем искать в виде .





Получили: - горизонтальная асимптота.

6. 
   Находим интервалы убывания, возрастания, экстремумы функции. Для этого найдем производную и решим уравнение .
   

Производная не обращается в нуль ни в одной точке. В точках 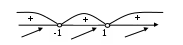производная не существует, но эти точки не принадлежат области определения, поэтому точек экстремума нет. На числовой прямой изображаем точки и определяем интервалы убывания и возрастания функции.




В каждом из интервалов производная имеет положительный знак, следовательно функция возрастает на всей области определения.

7. 
   Определяем точки перегиба, интервалы выпуклости и вогнутости. Находим вторую производную и решаем уравнение .
   

Критические точки . Для проверки достаточных условий выпуклости, вогнутости составляем таблицу.

	+		0	+	─
	Вогнутая	Выпуклая	0 Точка перегиба	Вогнутая	Выпуклая

8. 
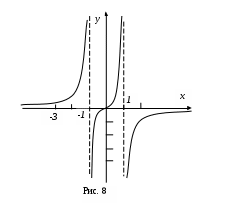   Строим график функции (рис. 8).
   

Дополнительные точки .