Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике

• Название: Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике
• Анкор: MU141.doc
• Дата: 17.08.2018
• Размер: 2.05 Mb.
• Имя файла: MU141.doc
• Тип: Методические указания; #23100
• страница: 16 из 17

3. Режимы обрыва фазы. Повторить измерения токов и напряжений при обрыве сопротивления нагрузки и линейного провода, сравнить их с параметрами симметричного режима и сделать выводы.

4. Сравнить измеренные значения токов и напряжений по каждому из пунктов исследования с расчётными. На векторные диаграммы, построенные при подготовке к работе, другим цветом нанести векторы, соответствующие экспериментальным данным.

5. Сформулировать заключение по работе.
Вопросы для самоконтроля
1. Напишите соотношения между линейными и фазными напряжениями и токами при соединении приемников в «треугольник».

2. Как изменяются линейные токи симметричного приемника при переключении его сопротивлений со «звезды» на «треугольник» и питании от одного и того же источника?

3. Как изменяются линейные токи симметричного приемника, соединенного «треугольником», при обрыве одной из его фаз?

4. Расскажите о порядке построения векторных диаграмм трехфазных цепей при соединении приемников в «треугольник».

5. Каковы преимущества и недостатки схемы соединения «треугольник» по сравнению со схемой соединения «звезда»?

6. Как изменяются линейные и фазные токи симметричного приемника, соединенного «треугольником», при обрыве одного из линейных проводов?
Лабораторная работа № 11

Исследование электрических цепей несинусоидального тока

Цель работы: экспериментальная проверка методики расчета линейных электрических цепей при несинусоидальных воздействиях и исследование влияния индуктивности и емкости на форму кривой тока.

Пояснения к работе

Методика расчета линейных электрических цепей несинусоидального тока состоит в том, что заданное несинусоидальное периодическое напряжение или ток источника аналитически или графоаналитически представляют в виде гармонического ряда Фурье, после чего выполняют расчет цепи по каждой гармонике отдельно и записывают результирующие значения мгновенных или действующих значений токов и напряжений на отдельных участках.

В общем случае периодическая несинусоидальная функция представляется рядом Фурье вида
f(t) = A₀ +A₁·sin(t+₁)+ A₂·sin(2t+₂)+…+ A_k·sin(kt+_k)+…, (11.1)

где A₀ - постоянная составляющая ряда Фурье или нулевая гармоника;

A₁·sin(t+₁) - основная гармоника ряда, имеющая одинаковый с несинусоидальной функцией период (частоту);

A_k·sin(kt+_k) - k -я гармоника ряда с частотой, в k раз большей частоты основной гармоники.

Если несинусоидальная периодическая функция f(t) имеет геометрически правильную форму и легко может быть представлена в виде аналитической функции, то ее разложение в ряд Фурье осуществляется аналитически согласно известным формулам. Результаты такого разложения приведены в справочниках.

При произвольной форме функции f(t) ее разложение в ряд Фурье осуществляется графоаналитическим методом. Этот метод основан на замене определенного интеграла суммой конечного числа слагаемых. С этой целью период несинусоидальной функции f(t) разбивают на n равных интервалов t= и интегралы заменяют алгебраической суммой n слагаемых. Постоянную составляющую A₀ ряда Фурье, амплитуду синусной составляющей A_kk -ой гармоники ряда и амплитуду косинусной составляющей A_kk -ой гармоники находят из выражений:
A₀ =  = (11.2)

A_k =  (11.3)

A_k =  (11.4)

Где: f(p)– значение несинусоидальной функции в конце p-го интервала (текущий индекс p принимает значения от 1до n),

sin(k·p) (cos(k·p))– значение синуса (косинуса) от аргумента в конце p-го интервала с учетом номера гармоники k.

Чем больше число интервалов, тем точнее результат разложения в ряд Фурье. На практике обычно достаточно разделить период на 24 или 18 интервалов.

Если несинусоидальная периодическая кривая симметрична относительно оси абсцисс, то на n равных интервалов разбивают полпериода и по формулам, аналогичным (11.2 – 11.4) находят гармонические составляющие ряда Фурье.

При замене синусного и косинусного рядов одинарным синусоидальным рядом фурье (11.1) используют следующие формулы:

A_k =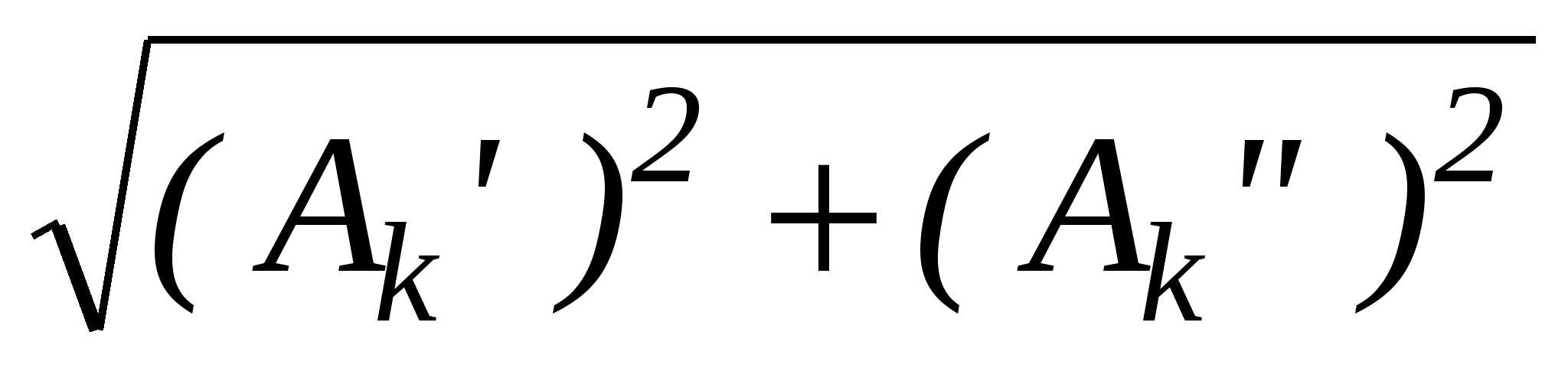, (11.5)

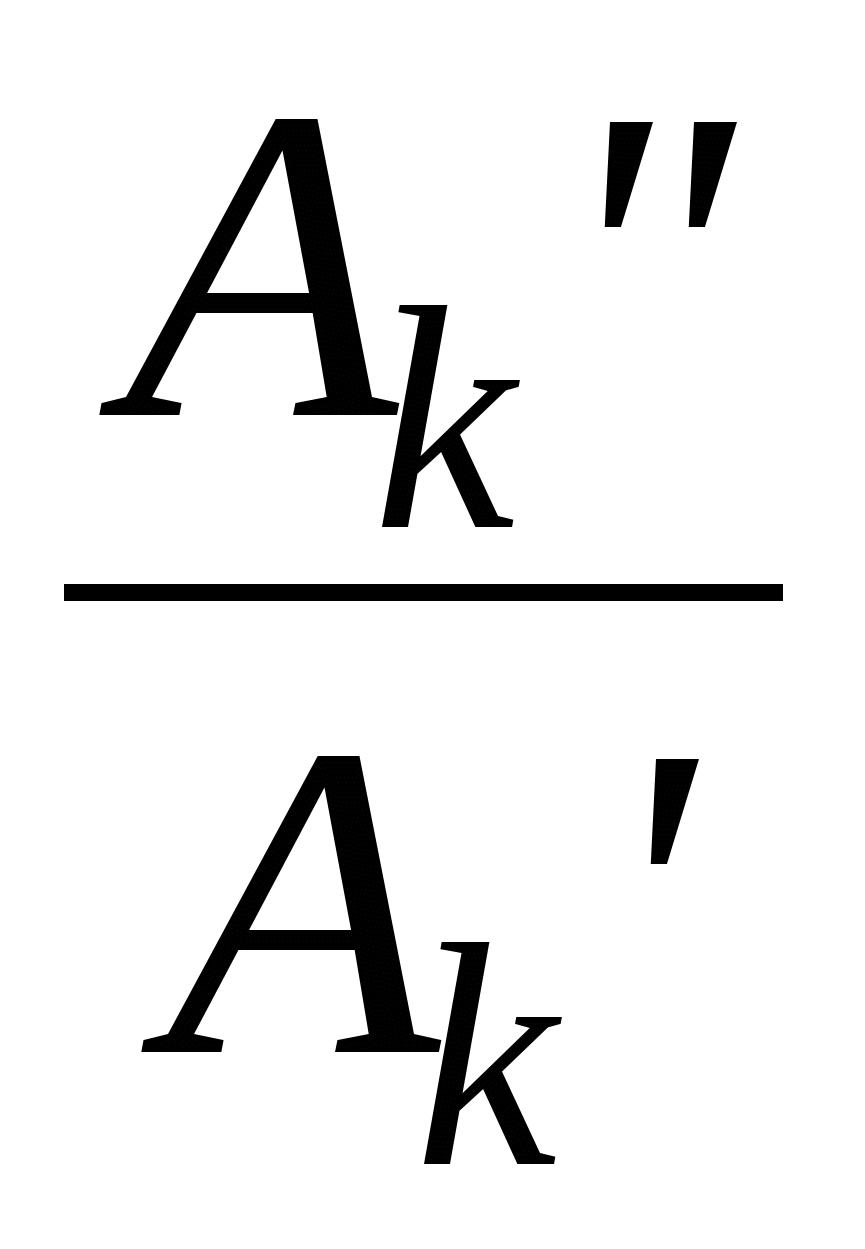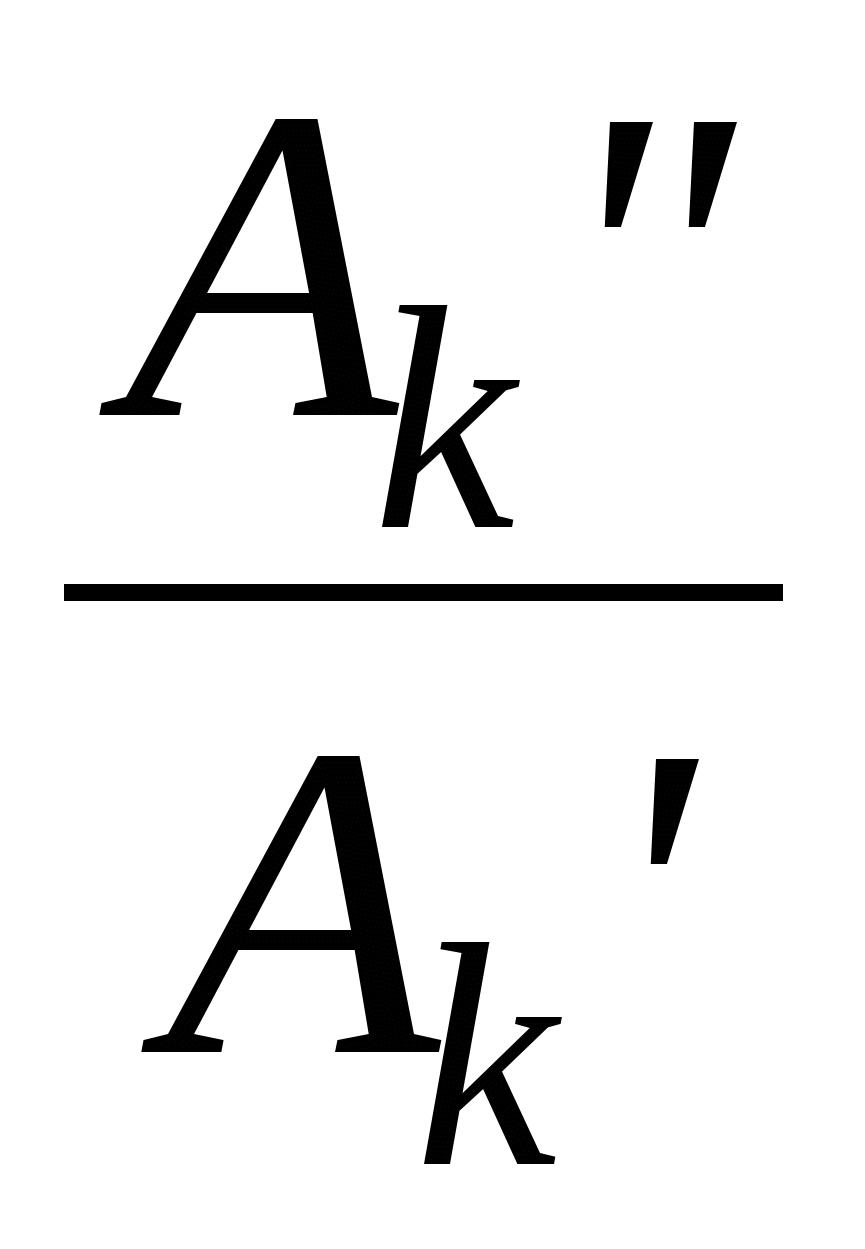_k = arctg, если A_k >0; _k =180^o+ arctg, если A_k <0, (11.6)

где A_k и _k– соответственно амплитуда и начальная фаза k –ой гармоники одинарного ряда.