Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике
 Скачать 2.05 Mb.
|
|
) и напряжения u = Um sin(t + u )= ImxLsin(t+ i + /2) определяется законом электромагнитной индукции: uL=L·di/dt , а напряжение на индуктивном элементе опережает ток по фазе на /2: = u- i = /2 (рис.4.2а). Последнее означает, что вектор напряжения опережает вектор тока на /2 (рис.4.2б). Амплитудные и действующие значения тока и напряжения на индуктивности связаны законом Ома: Um=ImxL, U=IхL , (4.2) где : хL =L=2fL - индуктивное сопротивление элемента. 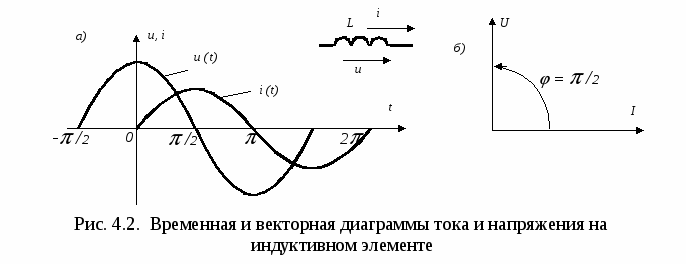 В ёмкостном элементе происходит преобразование электрической энергии источника в энергию электрического поля конденсатора. Связь между мгновенными значениями тока i = Im sin(t+i ) и напряжения u = Um sin(t+u )= Imxсsin(t+i - /2) определяется выражением i= c·du/dt,а напряжение на емкостном элементе отстает от тока по фазе на /2: 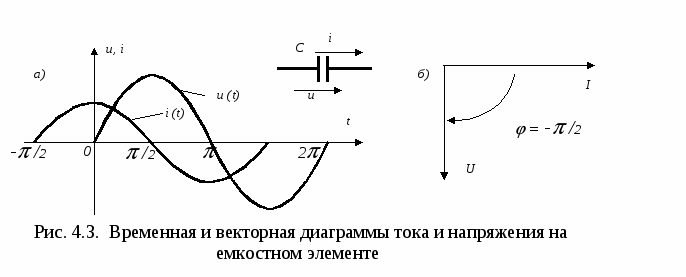 = u- i = - /2. (рис.4.3а). Последнее означает, что вектор напряжения отстает от вектора тока на /2 (рис.4.3б).Амплитудные и действующие значения тока и напряжения на ёмкости связаны законом Ома: Um=Imxс, U=Ixс , (4.3) где : xс =1/ С = 1/2fС - емкостное сопротивление элемента. Индуктивное xL и ёмкостное xC сопротивления называются реактивными сопротивлениями. При последовательном соединении активного r , индуктивного xL и ёмкостного xC сопротивлений (рис.4.4,а) мгновенное значение напряжения источника согласно второму закону Кирхгофа определяется алгебраической суммой мгновенных значений напряжений на отдельных элементах: u = ur+ uL+ uC , а действующее значение напряжения источника – векторной суммой действующих значений напряжений на отдельных элементах (рис.4.4,б) и может быть рассчитано по формуле : U =  = IZ (4.4)где : Z =  - полное сопротивление цепи при последовательном соединение элементов. В общем случае при наличии в схеме нескольких однородных элементов их эквивалентные величины определяются по формулам : r =   = r1 + r2+ . . . . + rn;xL =  = xL1 + xL2+ . . . . + xLn;xC =  = xC1 + xC2+ . . . . + xCn.Полное сопротивление цепи Z , активное r и реактивное x = xL - xC образуют треугольник сопротивлений (рис.4.4.в), для которого справедливы следующие соотношения: 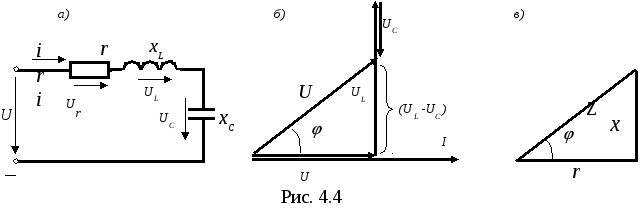 Z = , r = Z cos , x = Z sin , = arctg x/r (4.5)При параллельном соединении активного r , индуктивного xL и ёмкостного xC сопротивлений (рис.4.5,а) мгновенное значение тока источника согласно первому закону Кирхгофа равно алгебраической сумме мгновенных значений токов, протекающих через отдельные элементы: i = ir+ iL+ iC а действующее значение тока источника – векторной сумме действующих значений токов в отдельных элементах (рис.4.5б) и определяется формулой: I =  = U  = U ·y , (4.6)где : g=1/r – активная проводимость ; bL=1/xL – индуктивная проводимость ; bC=1/xC – ёмкостная проводимость ; b=bL-bC – реактивная проводимость ; y – полная проводимость цепи. В общем случае при параллельном соединении нескольких однородных элементов их эквивалентные величины определяются по формулам: g =  = g1 + g2 + . . . . + gn;bL =  = bL1 + bL2 + . . . . + bLn;bC =  = bC1 + bC2 + . . . . + bCn.Полная проводимость цепи Y, активная g и реактивная b проводимости составляют прямоугольный треугольник (треугольник проводимостей рис.4.5,в), для которого справедливы следующие соотношения: Y = 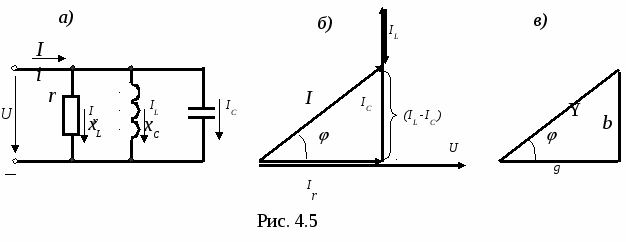 , g = Y cosj , b = Y sinj , j = arctg b/g (4.7)  Домашняя подготовка к работе 1. В соответствии с номером варианта выбрать рабочую схему с последовательным соединением элементов (рис.4.6). Из табл.4.1 согласно варианту выбрать элементы рабочей схемы. Таблица 4.1. Номера элементов схемы
2. Рассчитать сопротивления выбранных элементов при частоте 1 кГц, результаты расчета занести в табл. 4.2. Таблица 4.2. Расчетные сопротивления элементов
3. Для рабочей схемы с последовательным соединением рассчитать полное сопротивление цепи, ток и напряжения на участках цепи. Напряжение источника принять равным 20 В (f=1 кГц). Выполнить построение векторной диаграммы напряжений. Результаты расчёта занести в табл.4.3. Таблица 4.3. Результаты для схемы с последовательным соединением.
4. В соответствии с номером варианта выбрать рабочую схему с параллельным соединением элементов (рис.4.7). Из табл. 4.4 согласно варианту выбрать элементы рабочей схемы. 5. Рассчитать проводимости выбранных элементов при частоте 1 кГц, результаты расчета занести в табл. 4.5. Таблица 4.4. Номера элементов схемы
Таблица 4.5. Расчетные проводимости элементов
6. Для рабочей схемы с параллельным соединением рассчитать полную проводимость цепи и токи на участках цепи. Напряжение источника принять равным 5В (f=1 кГц). Выполнить построение векторной диаграммы токов. Результаты расчёта занести в табл.4.6. Таблица 4.6. Результаты для схемы с параллельным соединением.
Порядок выполнения работы 1. Собрать рабочую схему с последовательным соединением элементов. Установить напряжение U = 20 В при частоте f=1 кГц (использовать блок источников переменного напряжения). 2. Выполнить измерения напряжений и тока. Результаты измерений занести в табл.4.3. Сопоставить расчётные и экспериментальные значения величин и сделать выводы. 3. Собрать рабочую схему с параллельным соединением элементов. Установить напряжение U = 5 В при частоте f=1 кГц (использовать блок источников переменного напряжения). 4. Выполнить измерения токов различных участков цепи. Результаты измерений занести в табл.4.6. Сопоставить расчётные и экспериментальные значения величин и сделать выводы. 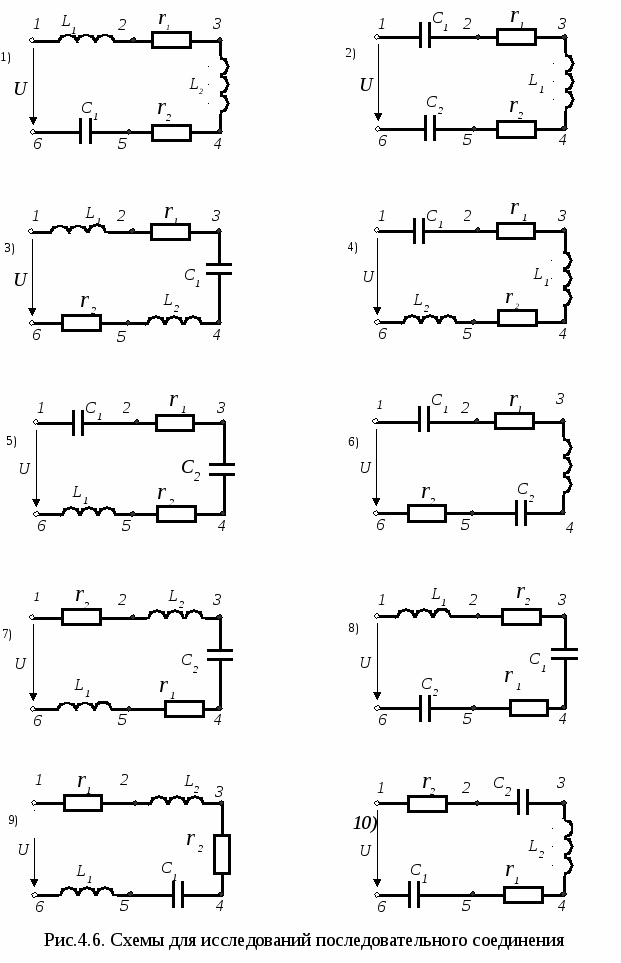 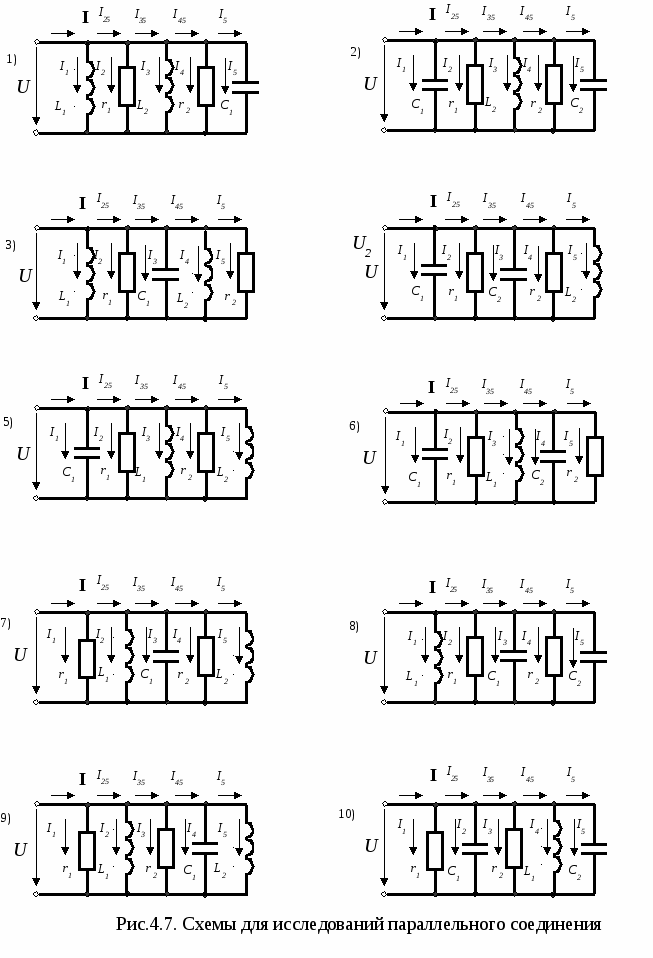 Вопросы для самоконтроля 1. Каков физический смысл активного, индуктивного и ёмкостного сопротивлений? 2. Как зависят активное, индуктивное и ёмкостное сопротивления от частоты? 3. Чему равны углы сдвига фаз между напряжением и током в активном сопротивлении, индуктивном и ёмкостном? 4. Как изменяется ток в схеме при последовательном соединении цепи r, L, C, если уменьшать ёмкость конденсатора? 5. Как изменится ток в общей части цепи при параллельном соединении r, L, C, если увеличить индуктивность катушки? 6. Каков порядок построения векторной диаграммы цепи при последовательном соединении элементов? 7. Каков порядок построения векторной диаграммы цепи при параллельном соединении элементов? Лабораторная работа № 5 Исследование разветвленных цепей синусоидального тока Цель работы: исследование разветвленных цепей синусоидального тока и экспериментальная проверка методов их расчёта. Пояснения к работе Состояние электрической цепи определяется различными факторами: активной и реактивной мощностями, токами в ветвях, напряжениями на элементах цепи и пр. Ответы на эти вопросы можно получить по результатам расчета и по результатам экспериментальных исследований. Для расчёта разветвлённых цепей синусоидального тока с одним источником питания применяют метод проводимостей, основанный на использовании векторных диаграмм (расчёт по активным и реактивным составляющим величин) и преобразований электрических цепей, а также универсальный метод комплексных амплитуд, который иначе называется символическим. Метод проводимостей основан на эквивалентных преобразованиях электрических цепей при последовательном и параллельном соединениях: преобразовании последовательно соединенных активного и реактивного элементов в параллельное и наоборот. При расчёте используют соотношения, вытекающие из векторной диаграммы, треугольников сопротивлений и проводимостей. Символический метод применяют при расчёте электрических цепей синусоидального тока произвольной сложности (несколько источников питания, соединение элементов треугольником или звездой и др.). Сущность метода заключается в том, что в цепях синусоидального тока законы Кирхгофа для действующих и амплитудных значений справедливы в векторной форме. Для операций с векторными величинами используются комплексные числа, изображающие комплексы ЭДС, комплексы напряжений, комплексы токов, комплексы сопротивлений и т.д. Подобно цепям постоянного тока, многообразие расчётных методов которых базировалось на использовании законов Ома и Кирхгофа, для цепей синусоидального тока эти методы также справедливы для величин в комплексной форме. Поэтому для расчёта цепей синусоидального тока можно использовать весь расчётный аппарат цепей постоянного тока: методы контурных токов, наложения, эквивалентного генератора, преобразования цепей и т.д. , но в этих уравнениях токи, напряжения, ЭДС и сопротивления должны фигурировать в комплексной форме:  E 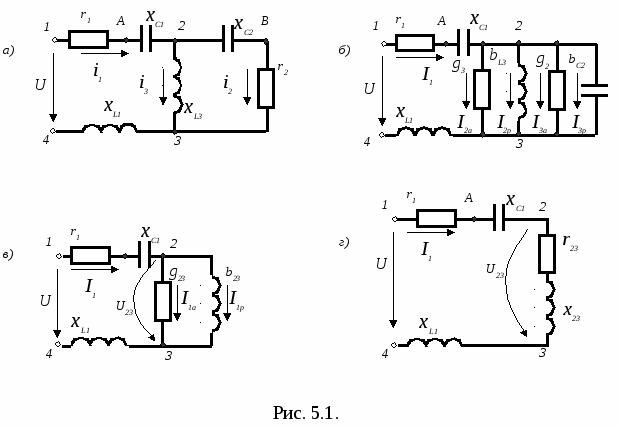(5.1) В  качестве примера рассмотрим расчёт токов в схеме рис.5.1 при напряжении источника U=15 В и частоте 1 кГц. Параметры схемы представлены в табл.5.1. Таблица 5.1. Характеристика элементов схемы рис.5.1
Расчёт с использованием метода проводимостей выполняем в следующем порядке: 1. В параллельно включённых ветвях исходной схемы заменим последовательные соединения элементов эквивалентными параллельными ветвями (рис.5.1б) :  , ,g3 = 0,  .2. Объединим параллельно включенные ветви, имеющие однородный характер (активные и реактивные), и получим схему рис.5.1в g23 = g2+g3=0,00306+0 = 0,00306 См ; b23= bL3 - bC2= 0,00532 - 0,00244 = 0,00288 См ; (индуктивный характер) y23=  = = 0,00420 См .3. Выполним эквивалентную замену параллельных ветвей последовательной ветвью (рис.5.1г) r23 = g23/ y23 2= 0,003062382 = 173Ом, x23=b23 / y23 2 = 0,002882382 =163 Ом (x23 имеет индуктивный характер, так как bL3 > bC2 ) z23 = 1/ y23 = 1/0.0042 = 238 Ом. 4. Определяем полное сопротивление цепи (рис.5.1г):  = = 588 Ом.5. Вычисляем ток в неразветвлённой части цепи:  A = 25,5 мА.Или иначе : I1a=Ug23 , I1р= Ub23 , I1 =  6. Находим напряжения на отдельных участках электрической цепи: U1A=I1r1=0,0255300=7,65 B, UA2=I1 xC1= 0,0255127=3,24 B, U23 = I1Z23 = 0,0255238=6,07 B, U34=I1xL1=0,0255314=8,01 B. 7. Определяем активные, реактивные и полные токи в ветвях: I2a=U23g2 = 6,07 0,00306 = 0,0186 A, I2p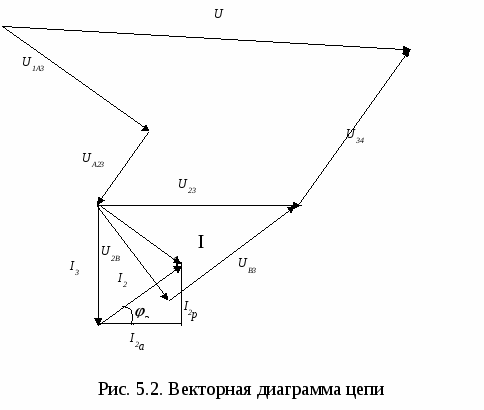=U23 bC2 = 6,070,00244 = 0,0148 A,I2 =  = =0,0238 A,I3 = I3p= U23bL3 = 6,07 0,00532 = 0,00323A .Н  а рис.5.2 представлена векторная диаграмма электрической цепи рис.5.1. Построение векторной диаграммы начинаем с вектора напряжения U23, положение которого может быть произвольным. Остальные векторы напряжений и токов имеют строго определённые положения относительно выбранного вектора U23.Далее выполняется построение векторной диаграммы токов. Вектор тока I3 отстаёт по фазе (повернут по часовой стрелке) на 90 от вектора напряжения U23 вследствие индуктивного характера сопротивления третьей ветви. Ток I2 имеет активно-емкостный характер, поэтому его вектор опережает (повернут против часовой стрелки) на угол 2 =arctgxС2/r2вектор напряжения U23. Построение вектора тока I2 может быть выполнено по составляющим: активная составляющая I2а совпадает с напряжением U23 ,реактивная (емкостная) составляющая I2р опережает U23 на 90. Ток в неразветвлённой части цепи согласно первому закону Кирхгофа равен векторной сумме токов в параллельно включённых ветвях: I1 = I2 + I3 . П  остроение векторов напряжения UA2, U1A, U34 осуществляем относительно вектора тока I1. По отношению к току I1вектор UA2 = I1 xС1(напряжение на емкости) отстаёт на 90, U1А =I1 r(напряжение на активном сопротивлении) совпадает, а U34(напряжение на индуктивном элементе) опережает на 90. Согласно второму закону Кирхгофа в комплексной форме: U = U34+U23+UA2+U1A, а U23 =UВ3+U2В, причем UВ3 = I2 r2 совпадает с током I2, а U2В= I2 xС2 отстаёт от этого тока на 90.При построении векторных диаграмм сложение векторов токов и напряжений согласно законам Кирхгофа производим в любой последовательности, однако, если требуется совместить векторную и топографическую диаграммы, то сложение векторов напряжений производится строго в той же последовательности, в которой они находятся на схеме. И каждый вектор напряжения на диаграмме определяет положение комплексных потенциалов соответствующих узлов схемы, причём конец вектора указывает положение той точки, которая в индексации напряжения стоит первой. Расчёт схемы рис.5.1 символическим методом выполним в следующем порядке.
U = U=15 В (напряжение источника направляем по вещественной оси), z1= z11+z111 = r1–jxС1 + jxL1 = 300 – j127 + j314 = 300 + j187 Ом , z 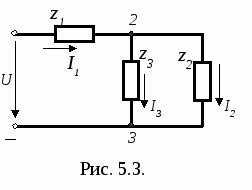 2=r2–jxС2 = 200 – j159 Ом ,z3 = jx3 = j188 Ом . Схема имеет вид, представленный на рис. 5.3.
 = 173 + j163 = 238 e j 43 Ом ,  = 300 + j 187 + 173 + j163 = 473 + j 350 = 588 e j 36,6Ом
0,0205 – j 0,0152 = 0,0255 e -j 36,6A.
U23 = I1Z23 = (0,0205 - j 0,0152)(173+j163) = 6,03+j0,71= 6,07e j 6,7 B,  
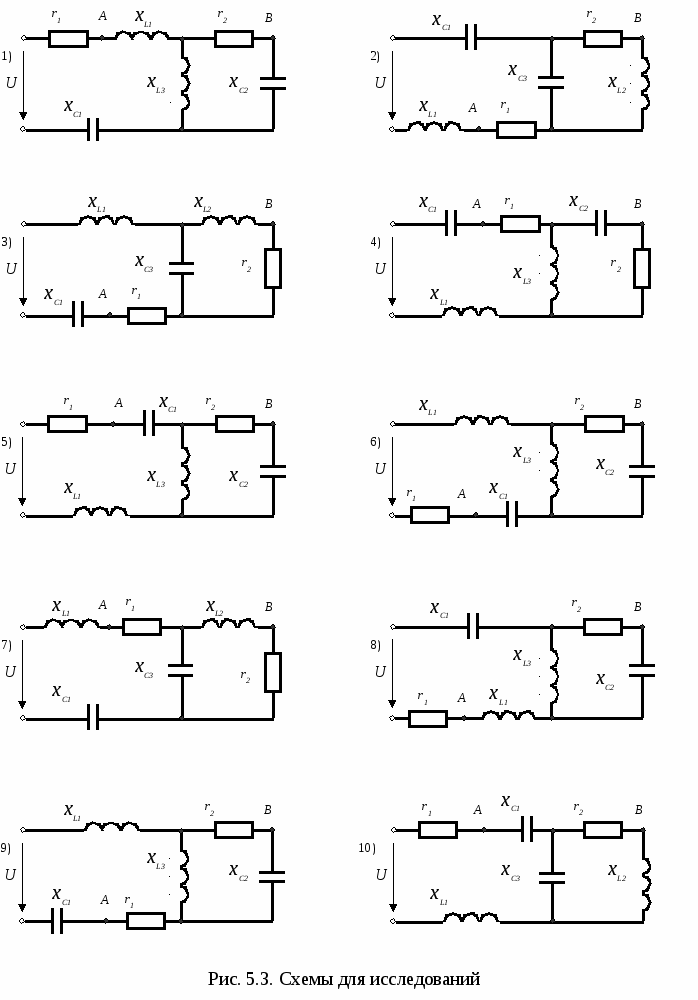
U1A =I1r1=(0,0205-j0,0152)300=6,15-j4,56 = 7,66e-j 36,6 B, UA2=I1(–j xС1 )=(0,0205-j0,0152)(-j127) = -1,93-j2,6 = 3,24e-j 126,6 B, U23=I1Z23 = (0,0205-j0,0152)(173+j163) = 6,03+j0,71 = 6,07e j 6,7 B, U34=I1 j xL1= (0,0205-j0,0152)j314 = 4,77+j6,44 = 8,02e j53,4 B 6. Напряжение между точками А и В : UAВ= UA2 + I2(–j xС2 )= –1,93 – j 2.6 + (0,0168+j0,0169)( –j159) = = –1,93 – j2.6 –j2.67 + 2,69 = 0.76 –j 5,27 = 5,32 e –j 81,8 B Домашняя подготовка к работе 1. Ознакомиться с методами расчёта цепей синусоидального тока и освоить методику построения векторных диаграмм электрических цепей. 2. Согласно номеру варианта по рис.5.3 выбрать рабочую схему (номер варианта соответствует номеру схемы) и по табл.5.2 выбрать номера элементов, используемых в схеме. Рассчитать сопротивления элементов при частоте ƒ=1 кГц. Данные занести в таблицу 5.3. 3. Используя метод проводимостей, рассчитать напряжения и токи в схеме рис.5.3 при напряжении источника U=15 В. Результаты расчёта занести в табл.5.4. Таблица 5.2. Номера элементов рабочей схемы.
Таблица 5.3. Характеристика элементов рабочей схемы.
4. Заменить параллельно включённые ветви схемы рис.5.3 эквивалентной ветвью и рассчитать её параметры r23, x23, L23 или C23. Данные занести в табл.5.4. 5. По данным расчёта построить в масштабе векторную диаграмму цепи, с помощью которой определить величину напряжения UAB межу точками А и В схемы. Результаты занести в табл.5.4. 6. Используя символический метод, рассчитать токи и напряжения в схеме рис.5.3 при напряжении источника U=15 В. Результаты расчёта занести в табл.5.4. Таблица 5.4. Результаты расчётов и экспериментов
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
огласно закону Ома в комплексной форме определяем ток в общей части цепи :