Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике
 Скачать 2.05 Mb.
|
|
Таблица 2.2. Результаты расчетов и экспериментов по методу узловых потенциалов
Таблица 2.3. Результаты расчетов и экспериментов по методу эквивалентного генератора
П  орядок выполнения работы 1. Собрать схему цепи рис.2.4, с помощью перемычек предусмотрев возможность измерения токов во всех ветвях. Проверить полярность и установить величины ЭДС источников Е1=19 В, Е2=15 В. 2. Применительно к схеме рис.2.4 проверить экспериментально выполнение принципа наложения. Сначала измерить частичные токи в ветвях схемы только при действии источника Е1=20 В (источник Е2 удален, а вместо него включена перемычка), затем выполнить измерения частичных токов только при источнике Е2. Наконец, включив оба источника, измерить полные токи ветвей. Результаты измерений записать в табл.2.1. Сделать вывод о точности выполнения принципа наложения в исследуемой цепи.
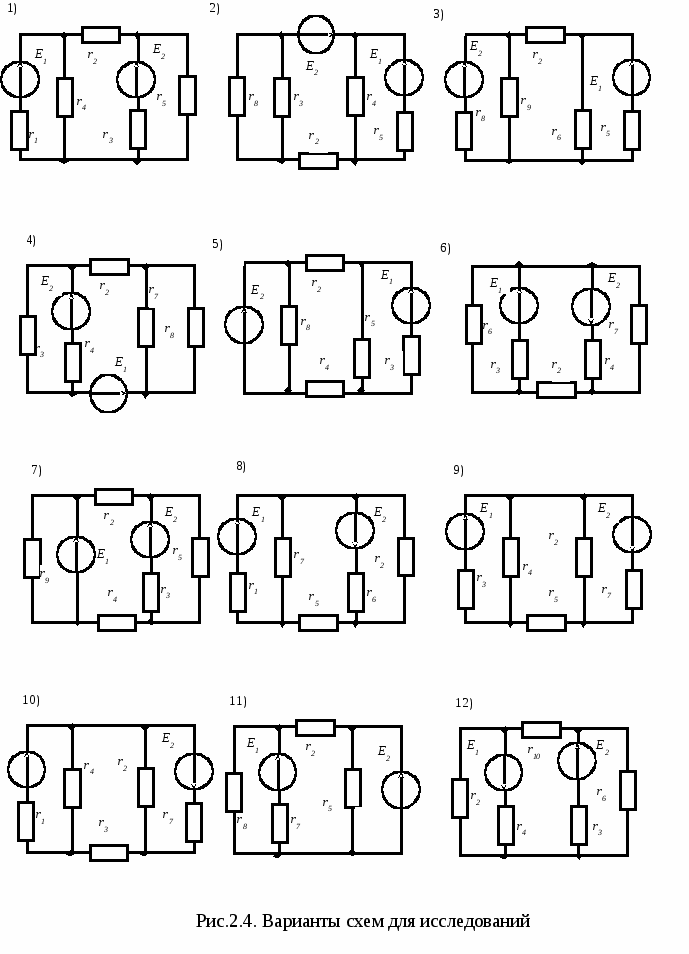 измерений занести в табл.2.2. Сделать вывод о точности совпадения расчетных и экспериментальных значений потенциалов узлов схемы. 4. Измерить токи в ветвях схемы рис.2.4 и результаты измерений занести в табл.2.2. Сравнить расчетные (по методу узловых потенциалов) и экспериментальные значения токов. 5. Осуществить экспериментальную проверку метода эквивалентного генератора. Для этого при включенных источниках ЭДС Е1 и Е2 необходимо удалить исследуемую ветвь с элементом 02 (сопротивление r2) в схеме рис.2.4 и, подключая к соответствующим узлам сначала вольтметр, а затем амперметр, измерить напряжение холостого ходаUxx и ток короткого замыканияIкз. По данным измерений рассчитать входное сопротивление пассивного двухполюсникаRвх=Uxx / Iкз, а затем ток I в удаленной ветви. Результаты исследований внести в табл.2.3. Сравнить расчетные и экспериментальные значения исследуемых величин. 6. Для контура цепи, включающего оба источника, построить потенциальную диаграмму, используя экспериментальные значения токов в ветвях. Привести результаты расчетов потенциалов всех узлов контура. Вопросы для самоконтроля 1. Сформулируйте принцип наложения. 2. В чем заключается сущность метода эквивалентного генератора? 3. Приведите порядок расчета электрической цепи с помощью метода узловых потенциалов. 4. Запишите систему уравнений для определения потенциалов двух узлов электрической цепи (третий узел заземлен). 5. Какие существуют способы экспериментального определения входного сопротивления относительно любой пары зажимов сложной электрической цепи? 6. В исследуемой схеме рис.2.4 определите величину входного сопротивления Rвх относительно ветви с источником ЭДС Е1. 7. Укажите порядок построения потенциальной диаграммы для замкнутого контура электрической цепи. 8. Запишите в общем виде формулу определения тока в ветви с несколькими ЭДС и несколькими сопротивлениями через потенциалы узлов, к которым она подключена. ЛАБОРАТОРНАЯ РАБОТА № 3 Определение условий оптимальной передачи электрической энергии от источника к приёмнику Цель работы: экспериментальная проверка теоретических положений об оптимальной передаче энергии от активного двухполюсника (источника) к пассивному двухполюснику (нагрузке) через промежуточное звено (линию передачи). Пояснения к работе Двухполюсник - это обобщённое название схемы или её части, рассматриваемой относительно пары зажимов. Если внутри двухполюсника есть источники ЭДС или тока, то двухполюсник называется активным. В противном случае двухполюсник называется пассивным. Активный двухполюсник по отношению к пассивному выступает в роли источника, а пассивный по отношению к активному – в роли приёмника (нагрузки). Активный двухполюсник характеризуется: - максимально возможным напряжением  , которое определяется как напряжение холостого хода;- максимально возможным током  , который определяется как ток короткого замыкания;- отношение к 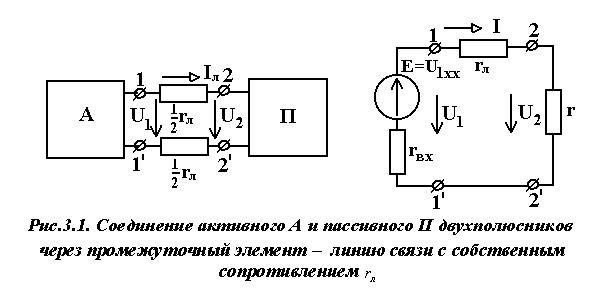определяет так называемое внутреннее (входное) сопротивление двухполюсника  .П  ассивный двухполюсник характеризуется только входным (внутренним) сопротивлением  . Схема связи между активным А и пассивным П двухполюсниками может содержать дополнительные элементы, например, линию связи (рис.3.1), характеризуемую сопротивлением  Если  , то имеет место непосредственная связь двухполюсников (рис. 3.2). Активная мощность  , расходуемая в пассивном двухполюснике, может быть рассчитана по формуле где  - ток в цепи – то есть и в нагрузке (см.рис.3.1 и 3.2).Ток в цепи можно рассчитать либо по формуле  (для схемы рис.3.1)либо по формуле  (для схемы рис.3.2),поэтому выражения для мощности нагрузки  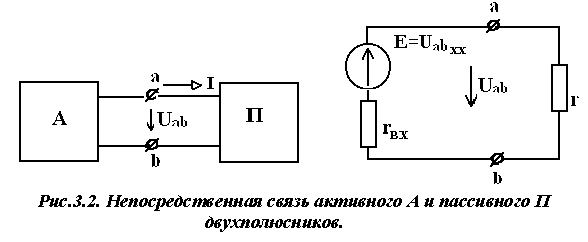приобретают следующий вид:  - (для схемы рис.3.1) и  - (для схемы рис.3.2).где  и  - напряжения на выходных зажимах активного двухполюсника в соответствующих схемах рис.3.1 и рис.3.2.Чтобы определить, при каком сопротивлении пассивного двухполюсника его потребляемая мощность будет максимальной, необходимо исследовать функцию  на экстремум. Для этого следует взять производную  и приравнять её к нулю. .Отсюда  . Для случая отсутствия линии ( )  .Можно убедиться в том, что при  ,  .Равенства  можно достичь или путём подбора при заданных и , или путём подбора при заданных и , или путём подбора при фиксированных (заданных) и . В последнем случае будут меняться также и ток активного двухполюсника. Операция подбора соответствующих сопротивлений для обеспечения указанного равенства, определяющего максимум мощности , называется согласованием нагрузки. При  условия можно достичь за счёт изменения величины сопротивления нагрузки .КПД (коэффициент полезного действия) источника (активного двухполюсника)  в схеме рис.3.1 определяется из выражения  .При этом  =0.5, если ( )=. Аналогично, для схемы рис.3.2 =0.5 при , то есть, если сопротивление нагрузки (для случая рис.3.1 () – есть сопротивление нагрузки) равно внутреннему сопротивлению источника, то коэффициент полезного действия источника равен 0.5 (или 50%).Из формулы видно, что КПД источника возрастает при увеличении сопротивления нагрузки . (Говорят, что если сопротивление нагрузки линии возрастает, то нагрузка линии (её нагрузка) убывает, то-есть линия разгружается!). КПД источника достигает максимального значения (равного 1) при его работе в режиме холостого хода (то есть, когда ток через линию равен нулю). Мощность в нагрузке при этом равна нулю. При уменьшении до нуля стремится к пределу  . В случае   при  .По отношению к схеме рис.3.1 можно говорить о КПД  линии передачи: .Домашняя подготовка к работе 1. В соответствии с номером варианта табл. 3.1 нарисовать схему исследуемого активного двухполюсника (см. рис.3.3 и рис.3.4). 2. Рассчитать напряжение холостого хода , т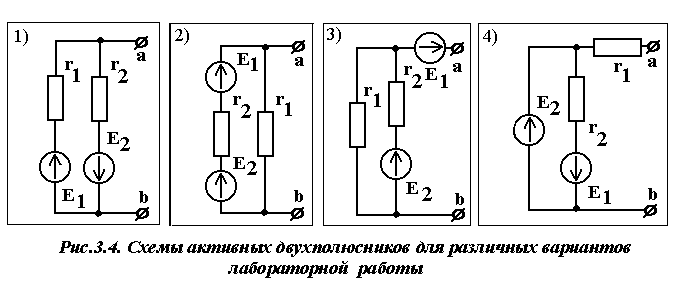ок короткого замыкания и  входное сопротивление активного двухполюсника (рис.3.4). Данные вычислений свести в табл.3.2. 3. Нарисовать эквивалентную расчётную схему исследований цепи (подобную рис.3.1) с указанием в ней значений  и (табл.3.1).4. Вычислить значение сопротивления |