Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике

• Название: Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике
• Анкор: MU141.doc
• Дата: 17.08.2018
• Размер: 2.05 Mb.
• Имя файла: MU141.doc
• Тип: Методические указания; #23100
• страница: 8 из 17

U

U

U

U

U

U

U

U

U

U

Порядок выполнения работы
1. Собрать рабочую схему рис.5.3 и установить напряжение источника U=15 В.

2. Измерить напряжения и токи в рабочей схеме, результаты измерений занести в табл.5.4. Сравнить экспериментальные величины с расчётными, полученными согласно методу проводимостей и символическому методу и сделать выводы.

3. Собрать эквивалентную схему с последовательным включением элементов r₂₃, x₂₃ (L₂₃ или C₂₃ , использовать блоки переменных активных, индуктивных или ёмкостных элементов). При напряжении источника U=15 В измерить напряжения и токи в этой схеме. Результаты измерений занести в табл.5.5. Сделать выводы.
Таблица 5.5. Результаты экспериментальных исследований.

U, В	I1, мА	U1A, В	UA2, В	U23, В	U34, В

Вопросы для самоконтроля
1. Какова последовательность расчёта цепей синусоидального тока методом проводимостей?

2. В чём сущность символического метода расчёта цепей синусоидального тока?

3. Какова последовательность построения векторных диаграмм электрических цепей синусоидального тока?

4. Как записываются законы Ома и Кирхгофа в комплексной форме?

6. 
   Как заменить в электрической цепи синусоидального тока парал-лельно включённые ветви одной эквивалентной ветвью?
   

Лабораторная работа № 6
Исследование резонансных явлений
Цель работы: исследование и проверка основных соотношений и частотных характеристик при резонансе в последовательном и параллельном контурах.
Пояснения к работе
Резонансом называется такой режим пассивной цепи, содержащей индуктивности и емкости, при котором напряжение и ток на входе цепи совпадают по фазе. При резонансе входное реактивное сопротивление (или входная реактивная проводимость) цепи равно нулю.
i = I_m sin(t+_i ), u = U_m sin(t+_u ) , _u= _i ,  = _u- _i = 0.
В цепи с последовательным соединением r, L, C (рис. 6.1а) возникает резонанс напряжений. Этот режим цепи имеет место при условии:

х_L= х_С , х ₌ х_L- х_С =0 или L= (6.1)

Напряжения на индуктивности и емкости при резонансе равны по величине и противоположны по фазе, а напряжение на резистивном элементе равно напряжению источника (рис. 6.1б) .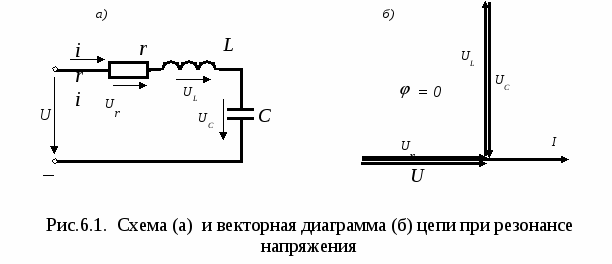





Из условия (6.1) следует, что резонанс достигается изменением параметров цепи: индуктивности или емкости, либо частоты напряжения источника питания. Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой:

. (6.2)

Индуктивное и емкостное сопротивления при резонансе называются характеристическим сопротивлением:

. (6.3)

Напряжения на индуктивности и емкости при резонансе могут значительно превышать напряжение источника, которое равно напряжению на активном сопротивлении:

U = Iz = Ir (6.4)

Отношение напряжения на индуктивности или емкости к напряжению источника при резонансе называют добротностью контура,
(6.5)

Зависимость параметров цепи x_L, ,x_C, ,x , z от частоты называют частотными характеристиками, а зависимости действующих (амплитудных) значений тока и напряжения от частоты – резонансными кривыми.

На рис.6.2 приведены частотные характеристики и резонансные кривые последовательного контура r, L, C. Для их построения использованы формулы:

, , ,

, , (6.6)

, .

К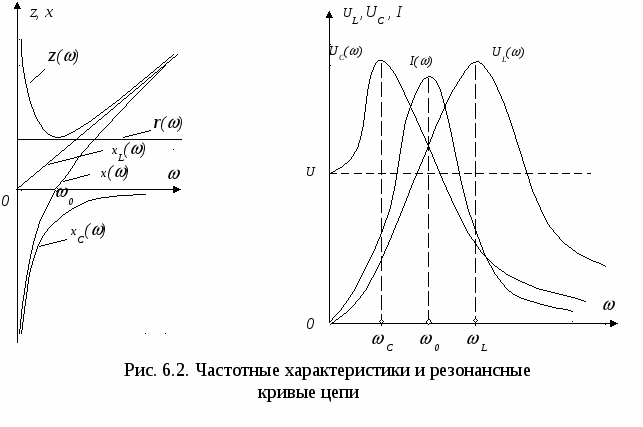ак следует из графиков (рис.6.2б), максимум тока наблюдается при резонансной частоте ₀ , а максимумы напряжений U_L и U_C соответственно при частотах _Lи _C:
, (6.7)

В цепи с двумя параллельными ветвями, содержащими индуктивности и емкости (рис.6.3а), резонанс наступает при равенстве нулю входной проводимости :
b = b_L1 - b_C2 = 0 , b_L1 = b_C2

где , (6.8)

В этом случае реактивные составляющие токов I_1p и I_2p равны по величине и противоположны по фазе (рис.6.3б). Величины токов в ветвях I₁ и I₂ могут значительно превысить ток в общей цепи I, поэтому резонанс в параллельном контуре получил название резонанса токов.

И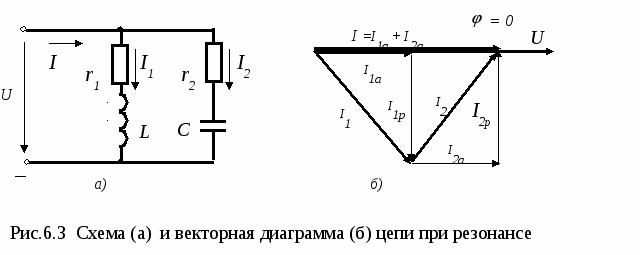
з (6.8) следует, что резонанс токов в рассматриваемой цепи можно достичь изменением пассивных параметров цепи r₁, r₂, L и C либо изменением частоты напряжения источника  .

Решение указанного соотношения относительно , дает значение для резонансной частоты:

(6.9)

Из полученного выражения следует, что резонанс токов возможен в случае, когда сопротивления r₁ и r₂ оба больше или оба меньше .

При r₁ = r₂ = 0 , получаем:

,

т.е. резонансная частота такая же, как и в последовательном контуре.

В случае, когда r₁ = r₂ = , имеет место резонанс при любой частоте.
Домашняя подготовка к работе
1. Используя данные табл.6.1, рассчитать индуктивность и емкость последовательного контура r, L, C. Данные расчета занести в табл.6.2.
Таблица 6.1. Исходные данные для расчета.

Резонансная частота f,kГц	4	5	4	5	4	5	4	5	4	5
Добротность	4	5	6	4	5	6	4	5	6	4
Активное сопротивление r, Ом	100	100	100	50	50	50	150	150	150	75

Номер варианта

1

2

3

4

5

6

7

8

9

10

2. При напряжении сети U = 5 В, рассчитать ток I₀, напряжения на индуктивности U_L0 и емкости U_C0 при резонансной частоте f₀., а также определить частоты, при которых напряжения на индуктивности и емкости достигают максимальных величин. Полученные результаты занести в табл.6.3.
Таблица 6.2. Результаты расчета.

r, Ом	L, мГн	С, мкФ

Таблица 6.3. Результаты расчета и эксперимента.

Исследуемые величины	f0 , кГц	I0 , мА	UC0 , В	UL0 , В	fL , кГц	fC, кГц
Расчет
Эксперимент

3. Для параллельного контура рис.6.3, используя те же реактивные элементы L и С, что и в последовательном контуре, при U = 5В и r₁ = r₂ = 100Ом, рассчитать резонансную частоту и токи в ветвях при резонансе токов. Результаты расчета занести в табл.6.4.
Таблица 6.4. Результаты расчета и эксперимента.

Исследуемые величины	f0 , кГц	I1 , мА	I2 , мА	I , мА
Расчет
Эксперимент

Порядок выполнения работы
1. В соответствии с номером варианта собрать схему рис.6.1а с последовательным соединением элементов r, L и C. Установить напряжение источника U=5Ви, изменяя частоту от 1до 9 кГц, снять резонансные кривые I(), U_L(), U_C().Результаты измерений занести в таблицу 6.5.
Таблица 6.5. Результаты измерений.

,кГц	1	2	3	4	5	6	7	8	9
I, мA
UL, B
UC, B

2. По данным табл.6.5 построить графики зависимостей I(), U_L(), U_C(). Определить частоты, при которых ток и напряжение достигают максимальных величин, а также числовые значения этих максимумов. Данные экспериментальных исследований занести в табл.6.3. Сопоставить результаты расчета и эксперимента и сделать выводы.

3. Собрать схему рис.6.3а с параллельным резонансным контуром, используя те же реактивные элементы L и С, что и в последовательном контуре и r₁ = r₂ = 100 Ом. Установить напряжение источника U=5Ви, изменяя частоту от 1 до 9 кГц, снять резонансные кривые I(), I₁(), I₂(). Данные экспериментальных исследований занести в табл.6.6.
Таблица 6.6. Результаты измерений.

, кГц	1	2	3	4	5	6	7	8	9
I, мA
I1, мA
I2, мA

4. В общей системе координат построить графики зависимостейI(), I₁), I₂(). Определить резонансную частоту и величины токов при этой частоте. Данные занести в табл.6.4. Сопоставить результаты расчета и эксперимента и сделать выводы.
Вопросы для самоконтроля

1. 
   Какой режим работы называют резонансным?
   
2. 
   В каких цепях можно наблюдать резонанс напряжений? Указать его характерные особенности.
   
3. 
   Постройте векторную диаграмму цепи при резонансе напряжений.
   
4. 
   Какой вид имеют частотные характеристики последовательного
   

резонансного контура?

5. Укажите все возможные способы достижения резонанса напряжений.

6. В каких цепях можно наблюдать резонанс токов? Указать его характерные особенности.

7. Постройте векторную диаграмму цепи при резонансе токов.

8. Какой характер имеют зависимости токов в ветвях параллельного резонансного контура от частоты при отсутствии резистивных сопротивлений?

9. Укажите все возможные способы достижения резонанса токов.

10. Приведите примеры использования на практике резонанса напряжений и резонанса токов.
Лабораторная работа № 7

Исследование явления взаимной индуктивности и неразветвленных цепей с индуктивно связанными элементами

Цель работы:

- экспериментальное определение параметров реальных катушек, имеющих индуктивную связь, нахождение их одноимённых зажимов и величины коэффициента связи;

- проверка расчетных соотношений, справедливых для последовательного и параллельного соединения элементов.