Методические указания по выполнению расчетно лабораторных работ по теоретической электротехнике
 Скачать 2.05 Mb.
|
|
5  . Записать и усвоить порядок выполнения работы в лаборатории, ознакомиться с контрольными вопросами к лабораторной работе.Порядок выполнения работы 1. Собрать схему рис.1.1 сначала с источником нерегулируемого, а затем с источником регулируемого постоянного напряжения при U=15В и снять нагрузочные характеристики этих источников. В качестве переменного сопротивления Rн принять резистор R4 в блоке резисторов стенда. Ток следует изменять в пределах 0-500 мА с шагом 100 мА. Холостой ход источника (I=0, Uхх=E) обеспечивается отключением резистора Rн. Результаты измерений внести в табл.1.1, по данным которой определить параметры Е и rв источников и в общей системе координат построить графики характеристик Uвых=(I). 2. Собрать схему рис.1.2 с источником регулируемого напряжения и исследуемыми резисторами 01 и 02. Изменяя напряжение источника от нуля до максимально допустимого, произвести измерения напряжений и токов, результаты которых внести в табл.1.2. Необходимо следить за тем, чтобы токи в резисторах не превосходили максимально допустимых значений. В общей системе координат построить вольт-амперные характеристики резистивных элементов U=(I). 3. По схеме рис.1.2 выполнить исследования для определения фактических сопротивлений резисторов стенда при токах, близких к их максимально допустимым значениям. Результаты измерений напряжений на резисторах и токов в цепи внести в табл.1.3. Вычислить сопротивления резисторов и сравнить их с номинальными значениями, определить относительную погрешность величины номинального сопротивления резистивных элементов. 4. Собрать схему рис.1.4 согласно номеру варианта электрической цепи, предусмотрев в ней возможность измерения токов во всех ветвях (в ветвях должны быть перемычки, вместо которых подключается прибор для измерения тока этих ветвей). В качестве источника использовать источник регулируемого напряжения c Uвх=18 В. Результаты измерений напряжения и токов в схеме рис.1.4 внести в табл.1.4. 6. Для схемы рис.1.4 составить уравнения по первому и второму законам Кирхгофа и убедиться в их выполнении, используя при этом экспериментальные значения напряжений, токов и сопротивлений. Сделать выводы по результатам лабораторной работы. Вопросы для самоконтроля 1. Запишите уравнение внешней характеристики реальных источников энергии и представьте ее график. 2. Каким образом экспериментально определяют параметры E и rв источника энергии? 3. Каким образом реальные источники энергии представляют в расчетных схемах и можно ли исследованные в работе источники представить в расчетных схемах идеальными источниками ЭДС? 4. Известны параметры E и rв реального источника энергии. Составьте его эквивалентную схему замещения с источником тока и определите ее параметры. 5. Параллельно включены 4 резистора с сопротивлениями: 2, 2, 8, 8 Ом. Определите входное сопротивление такой цепи. 6. Сформулируйте закон Ома и законы Кирхгофа для электрических цепей постоянного тока. 7. Общий ток в цепи, состоящей из двух параллельно включенных резисторов R1 =3 Ом, R2 =2 Ом, равен 10 А. Пользуясь правилом разброса тока в параллельные ветви, определите токи в каждом из сопротивлений. 8. Последовательно включено 4 резистора: 2, 8, 6, 4 Ом. Определите напряжение источника, если напряжение на последнем резисторе равно 16 В. ЛАБОРАТОРНАЯ РАБОТА № 2 Исследование сложной электрической цепи постоянного тока Цель работы: экспериментально проверить основные методы расчета линейных электрических цепей постоянного тока: принцип наложения, метод узловых потенциалов, метод эквивалентного генератора, а также построить потенциальную диаграмму для одного из контуров цепи. Пояснения к работе Принцип наложения присущ только линейным цепям. Он заключается в том, что ток любой ветви линейной цепи с несколькими источниками определяется алгебраической суммой частичных токов, создаваемых в этой ветви под действием каждого источника энергии в отдельности. В схеме оставляется только один источник энергии, а все остальные исключаются из цепи (заменяются их внутренними сопротивлениями). В качестве примера рассмотрим электрическую цепь, представленную на рис.2.1. Параметры элементов цепи известны: Е1=20 В, Е2=10 В, r1=50 Ом, r3=100 Ом, r4=150 Ом, r5=200 Ом, r6=75 Ом. 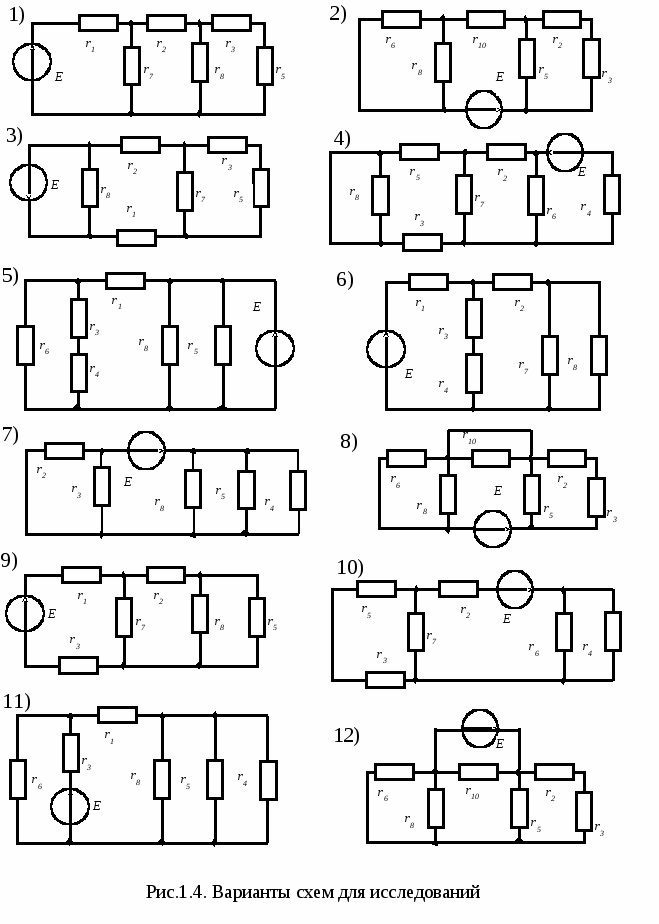 Т  ребуется определить токи в ветвях схемы с помощью метода наложения. С 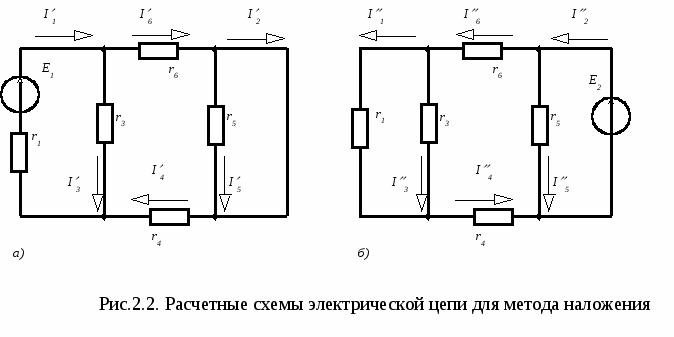 начала определим частичные токи в ветвях схемы при действии только ЭДС Е1 (рис.2.2,а):  А.  А, А.I4 =I2 =I6 =0,052 A, I5 =0 A. Затем находим частичные токи в ветвях схемы при действии только ЭДС E2 (рис.2.2,б):  А,  А, А, А, А,  А.Токи в исходной схеме рис.2.1 определяем согласно методу наложения в виде алгебраической суммы соответствующих частичных токов: I1 =I1 -I1=0,168-0,0258=0,142 A, I2 = -I2 +I2= -0,052+0,0887= 0,037 A, I3 =I3 + I3=0,116+0,0129=0,129 A, I4 = -I4 +I4= -0,052+0,0387= -0,013 A, I5 =I5 +I5=0 + 0,05=0,05 A, I6 =I6 -I6=0,052 - 0,0387= 0,013 A, Метод узловых потенциалов основан на применении первого закона Кирхгофа и закона Ома. При этом потенциал одного из узлов электрической цепи принимают равным нулю (узел заземляют), а для определения потенциалов остальных узлов схемы составляют и решают систему линейных алгебраических уравнений, полученных на основании первого закона Кирхгофа. Затем, используя закон Ома, рассчитывают токи в ветвях схемы. В качестве примера определим токи в ветвях схемы рис.2.1 методом узловых потенциалов. Принимаем 4 =0, тогда2 =Е2 =10 B. Составляем систему уравнений для определения потенциалов оставшихся узлов: 1(g1+g3+g6)- 2g6-3(g1+g3)= E1g1 , -1(g1+g3)+3(g1+g3+g4)= -E1g1 . Принимая во внимание, что  1/Ом,  1/Ом, 1/Ом,  1/Ом,получим 1·0,0433 - 3·0,03= 0,533 , -1·0,03+3·0,0367= - 0,4, или 1 = 10,97 В, 3 = - 1,93 В. Токи в ветвях вычисляем с помощью закона Ома: I1=(3 - 1 +E1)·g1=(-1,93-10,97+20)·0,02=0,142 A, I3=(1 - 3 )·g3=(-10,97+1,93)·0,01=0,129 A, I4=(3 - 4 )·g4=(-1,93-0)·0,0067= - 0,013 A, I5=(2 - 4 )·g5=(10 - 0)·(1/200)=0,05 A, I6=(1 - 2 )· g6=(10,97-10)·0,0133=0,013 A, I2= I4 + I5 = - 0,013+0,05= 0,037 A. Метод эквивалентного генератора. Метод применяется в том случае, когда требуется определить ток в одной ветви схемы. При этом из схемы выделяют искомую ветвь с сопротивлением r, а остальную часть схемы представляют в виде активного двухполюсника, который в свою очередь заменяют эквивалентным генератором. ЭДС Е эквивалентного генератора равна напряжению холостого хода Uхх двухполюсника, а внутреннее сопротивление генератора rв– входному сопротивлению Rвх пассивного двухполюсника. Тогда ток в выделенной ветви  .В качестве примера определим ток I6 в схеме рис.2.1. Сначала удалим из схемы сопротивление r6 и вычислим напряжение U.хх (рис.2.3,а). Согласно второму закону Кирхгофа  ,откуда  В,где  А,  0 А.Для определения входного сопротивления пассивного двухполюсника все источники из схемы удаляем, оставляя в ней их внутренние сопротивления (рис.2.3,б):  Ом.Искомый ток находим согласно закону Ома (рис.2.3,в) 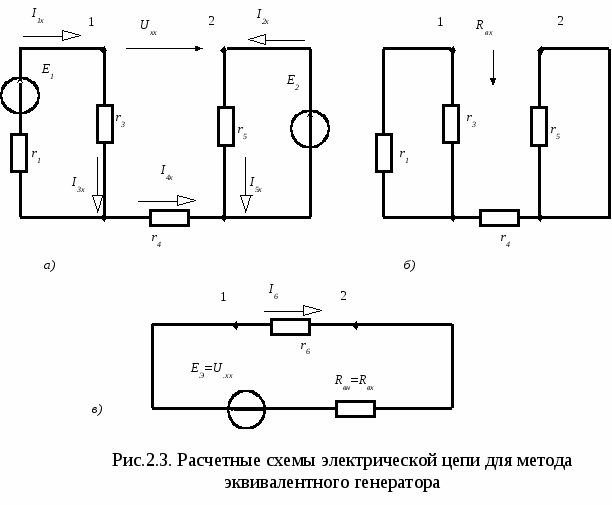  А.Домашняя подготовка к работе 1. В соответствии с номером варианта вычертить схему рис.2.4, обозначив сопротивления ветвей и произвольно выбрав положительные направления токов в ветвях. 2. Используя метод наложения, рассчитать токи в ветвях схемы рис.2.4 при Е1=19 В, Е2=15 В и результаты расчета занести в табл.2.1. Сопротивления схемы принять равными их номинальным значениям согласно табл.1.3 (номер сопротивления ветви равен номеру резистивного элемента стенда). 3. Используя метод узловых потенциалов, рассчитать схему рис.2.4 при Е1=19 В, Е2=15 В и результаты расчета занести в табл.2.2 (на схеме обозначить потенциалы узлов). 4. Используя метод эквивалентного генератора, при Е1=19В, Е2=15 В .рассчитать ток Iв ветви с элементом 02 схемы рис.2.4 и результаты расчета занести в табл.2.3. Таблица 2.1.Результаты расчетов и экспериментов по методу наложения
| |||||||||||||||||||||||||||||||||||||||||||||||||||||