|
ФинМен-КОНТР-Раб-08. Методические указания по выполнению, задания и последовательность работы
При проведении финансовых операций чрезвычайно важно знать как же соотносятся величины S и Sc. Все зависит от величины n. При 0Sc, при n>1 Sc. Г  рафически взаимосвязь S и Sc.можно представить следующим образом (рис.1).
Sc
S
1 Периоды начисления
Рис. 1.
Таким образом, в случае ежегодного начисления процентов для лица представляющего денежные средства в долг:
более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода)
более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно).
обе схемы дают одинаковые результаты при продолжительности периода один год и однократном начислении процентов.
При использовании простых процентов, когда срок ссуды не равен целому числу лет, периода начисления процентов выражают дробным числом, т.е. как отношение числа дней, на которое представили ссуду к числу дней в году:
 ,
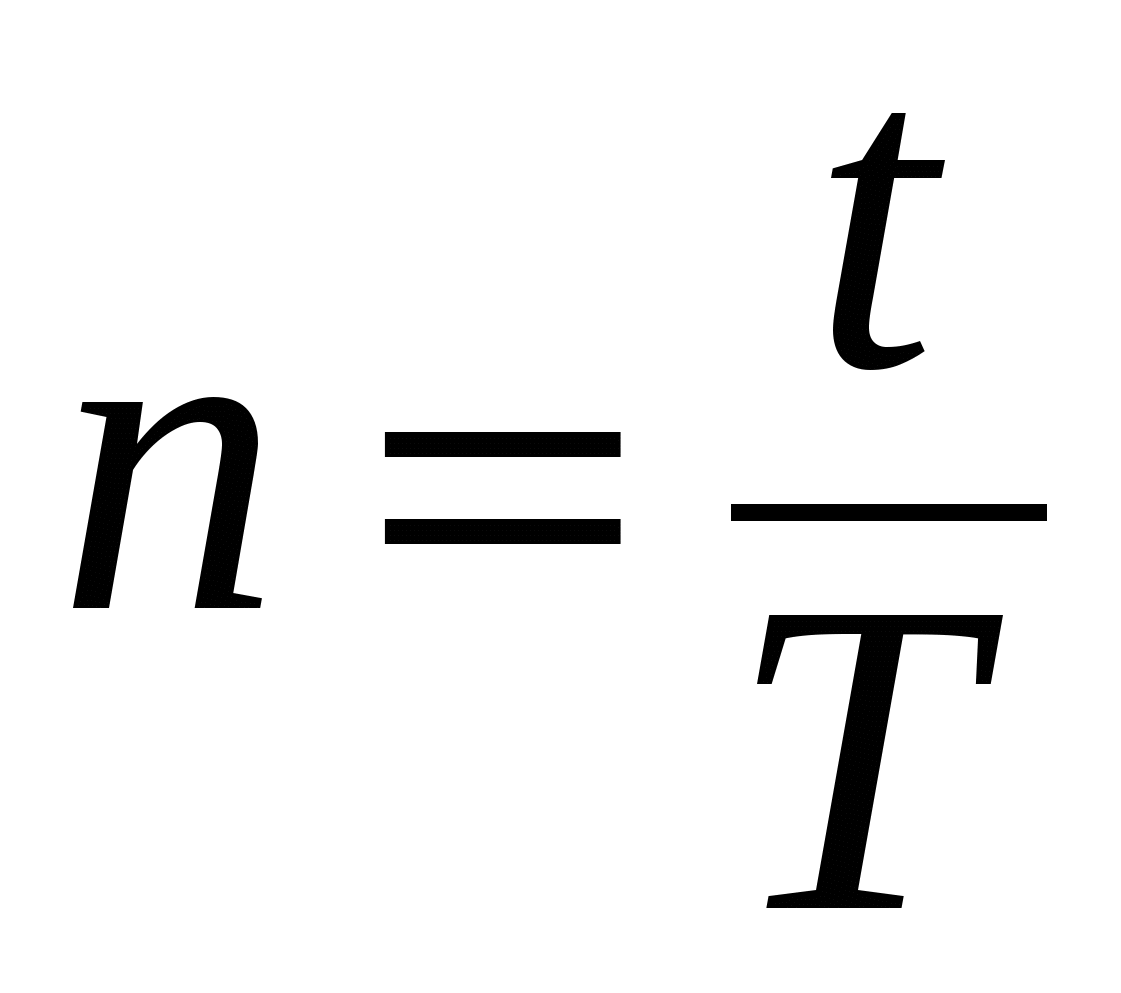где t – число дней, на которое предоставили ссуду;
Т – число дней в году.
В этом случае наращенная сумма денежных средств определяется по формуле:
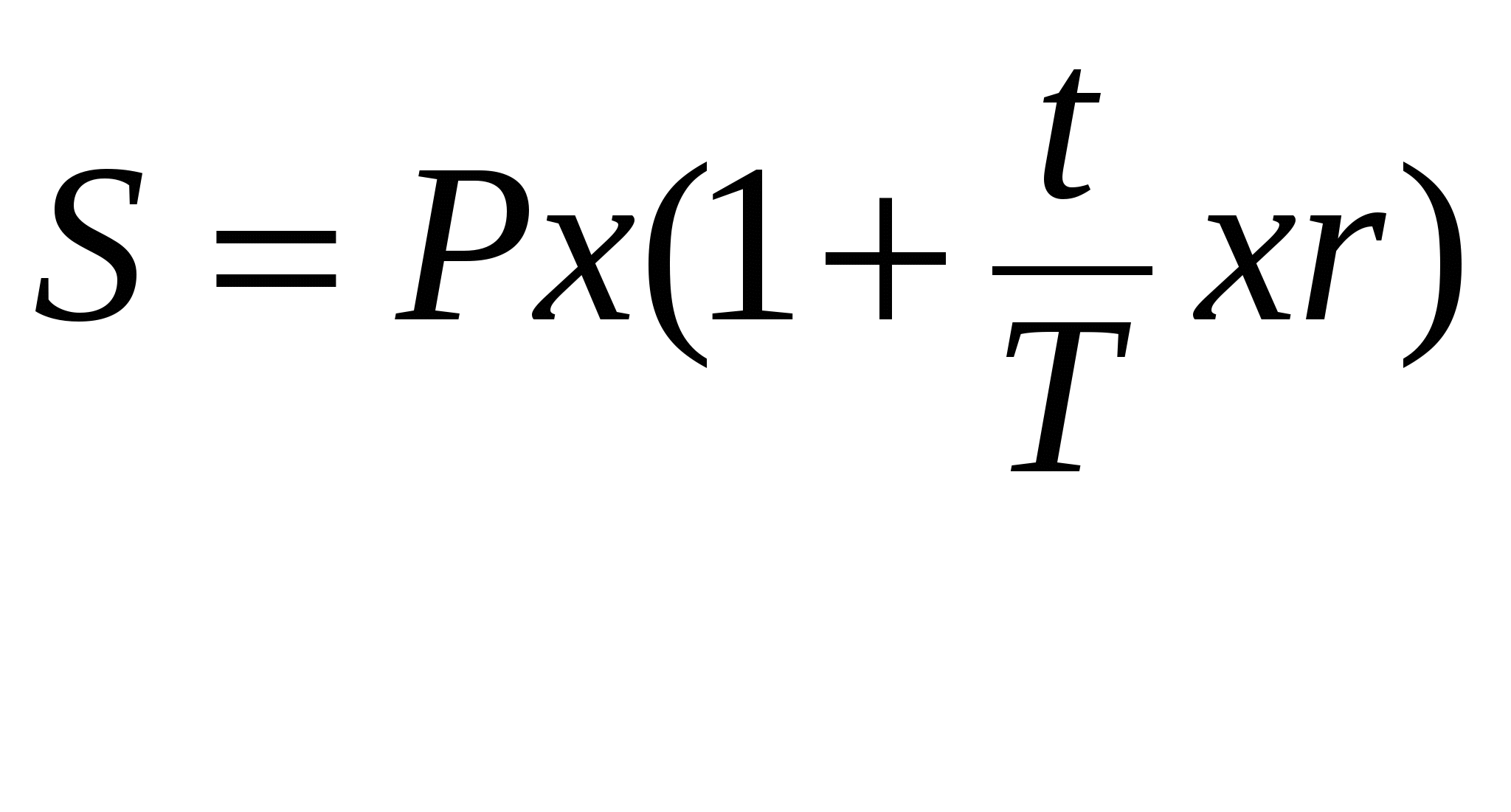
Для наглядности данную формулу можно записать следующим образом
 ,
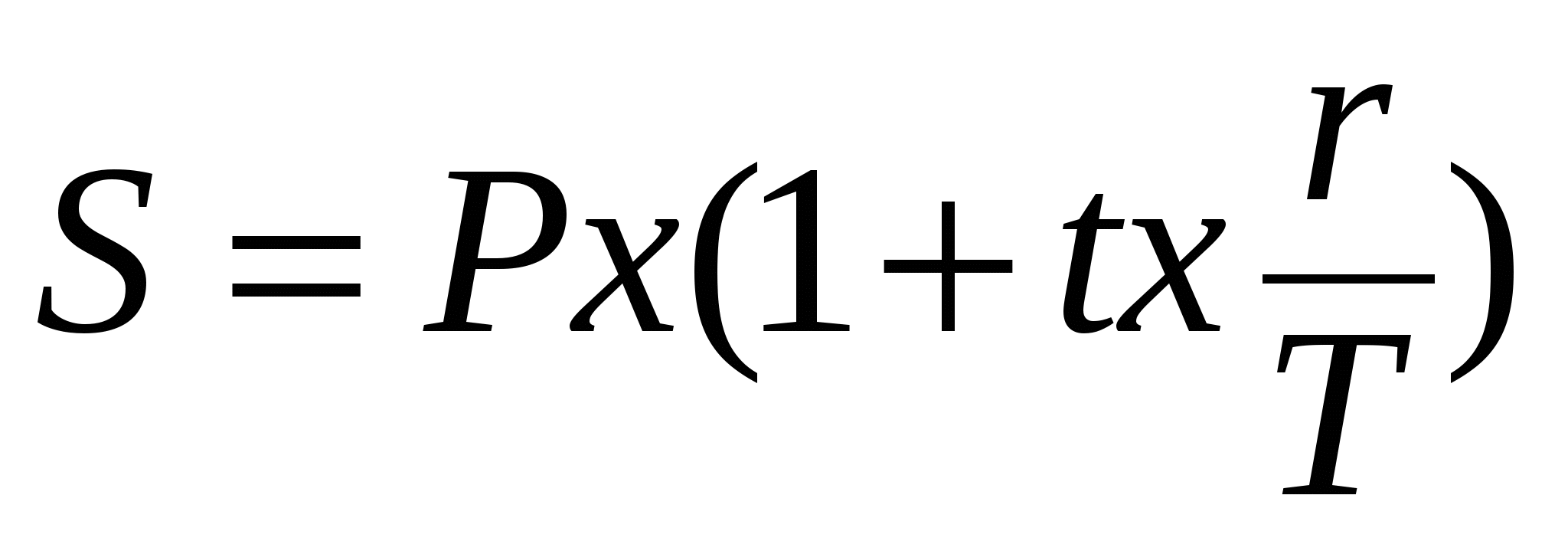где дробь r/T представляет собой дневную ставку, а произведение t x r/T – ставку за t дней.
В ряде стран для удобства вычислений год делится на 12 месяцев по 30 дней в каждом, т. е. продолжительность года (Т) принимается равной 360 дней. Это так называемая «германская практика». Проценты рассчитанные с временной базой 360 дней называются обыкновенными.
Существует «французская практика», когда продолжительность года принимается равной Т=360 дней, а продолжительность месяцев соответствует календарному исчислению. И, наконец, в ряде стран используется «английская практика», учитывающая продолжительность года в 365 дней, а продолжительность месяцев – в днях, также соответствующих календарному исчислению, как и при использовании «французской практики», т.е. 28, 29, 30 и 31 дней.
В этой связи различают три метода процентных расчетов, которые зависят от выбранного периода начисления;
1. Точные проценты с точным числом дней ссуды («английская практика»).
При этом методе определяется фактическое число дней (t) между двумя датами (датой получения и погашения ссуды), продолжительность ссуды принимается равной Т = 365/366 дней.
Для упрощения процедуры расчета точного числа дней пользуются специальными таблицами, в которых все дни в году последовательно пронумерованы. Продолжительность ссудо-заемной операции определяется вычитанием номера первого дня из номера последнего дня (приложение 1).
2. Обыкновенные проценты с точным числом дней ссуды («французская практика»), величина t рассчитывается, как и в предыдущем случае, продолжительность года принимается равной Т = 360 дней.
3. Обыкновенные проценты с приближенным числом дней ссуды («германская практика»); величина t определяется количеством месяцев по 30 дней в каждом, начисленная с момента выдачи ссуды и до момента ее погашения, и точным числом дней ссуды в неполном месяце, продолжительность года
Т = 360 дней.
В практическом смысле эффект от выбора того или иного способа зависит от значительности суммы, фигурирующей в процессе финансовой операции. Но и так ясно, что использование обыкновенных процентов с точным числом дней ссуды, как правило, дает большой результат.
Определяя продолжительность ссудо-заемной операции, принято день выдачи и день погашения ссуды считать за один день.
Нередко в контрактах на получение ссуды оговаривается величина годового процента и количество периодов начисления процентов. В этом случае расчет ведется по формуле сложных процентов по подпериодам и по ставке, равной пропорциональной доле исходной годовой ставки по формуле:
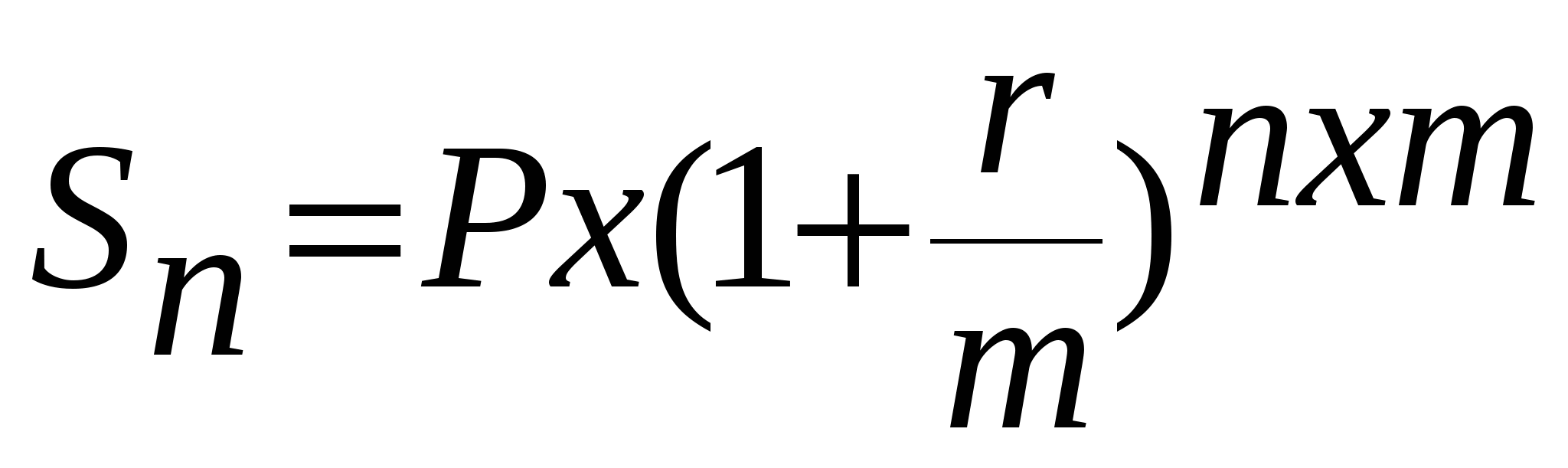
где - r – годовая процентная ставка
m – количество начислений в году
n – количество лет.
|
|
|
Скачать 0.94 Mb.