метод указ по ЦС для АТМ ЗОТ ЧАСТЬ 1. Методические указания
 Скачать 408.5 Kb. Скачать 408.5 Kb.
|
|
Тема 1.1. Формы представления числовой информации в цифровых устройствах Задачи 1-30 У 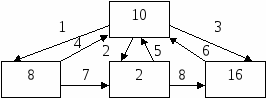 словие: Произвести перевод заданного десятичного числа (см. таблицу 2) в соответствии с расчётной схемой, изображённой на рисунке 1 (цифра в блоке означает наименование системы счисления, цифра над стрелкой – номер примера). При решении данной задачи должно быть решено 8 примеров. словие: Произвести перевод заданного десятичного числа (см. таблицу 2) в соответствии с расчётной схемой, изображённой на рисунке 1 (цифра в блоке означает наименование системы счисления, цифра над стрелкой – номер примера). При решении данной задачи должно быть решено 8 примеров.Рисунок 1. Расчётная схема Таблица 2 Исходные данные для решения задач 1-30
Методические указания к решению задач № 1-30 Для перевода дробного число Х10 в новую систему счисления (СС) с основанием q необходимо разбить его на целую и дробную части и воспользоваться следующими правилами. Правило перевода целой части дробного числа. Целую часть (целое число) необходимо последовательно делить на основание новой СС до тех пор, пока последнее частное не окажется меньше нового основания: 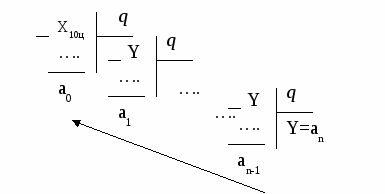 (1) где Х10ц – целая часть (целое число); q- основание новой системы; Y – частное; a0, а1,…, аn - остатки. Результат перевода целой части записывается в виде последовательности цифр, записанных слева направо начиная с последнего частного и кончая первым остатком и примет вид: Zqц= an an-1 ….a1 a0 , (2) Правило перевода дробной части числа. Для перевода дробной части (правильной дроби) необходимо провести последовательное умножение этой дроби и получившихся дробных частей произведения на основание новой СС: 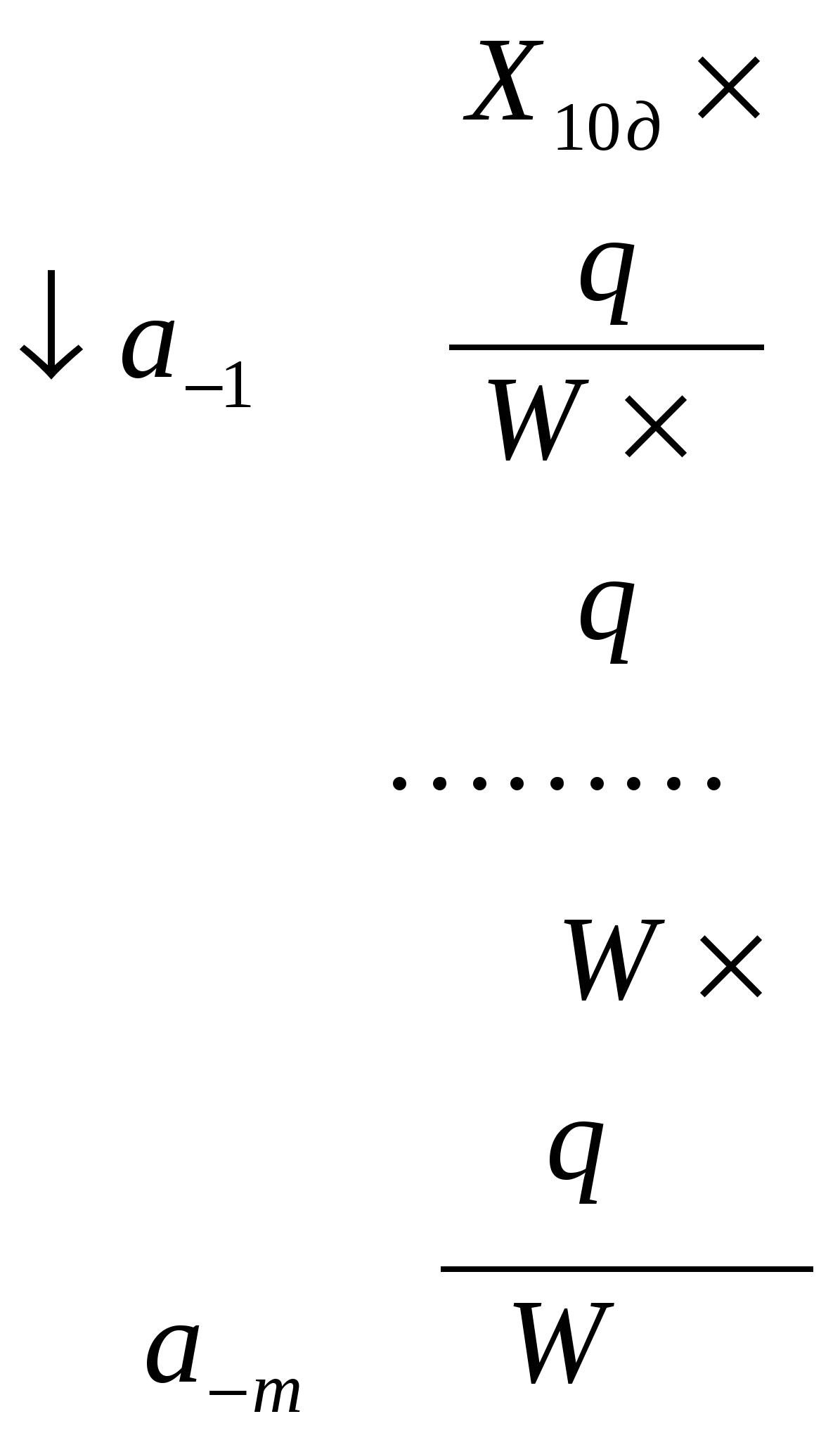 (3) где Х10д – дробная часть (правильная дробь); q- основание новой системы; W – произведение; a-1,…,а-m – промежуточные целые результаты. Результатом перевода дробной части будет являться прямая последовательность целых чисел: Zqд= 0, a-1 ……… a-m . (4) Конечный результат перевода дробного десятичного числа будет равен сумме промежуточных результатов: Zq = Zqц + Zqд =an an-1 ….a1 a0 ,a-1 ……… a-m . (5) 1.2. Воспользовавшись вышеприведёнными правилами и формулами в п.1.1 перевести заданное дробное число из десятичной СС 1.2.1. в восьмеричную СС с основанием q =8 (пример 1 расчётной схемы); 1.2.2. в двоичную СС с основанием q =2 (пример 2 расчётной схемы); 1.2.3. в шестнадцатеричную СС с основанием q =16 (пример 3 расчётной схемы).
Правило перевода дробного числа в десятичную СС. Для того чтобы перевести дробное число с основанием qв десятичную СС, необходимо представить его в форме полинома по степеням основания и раскрыть все члены этого полинома в десятичной СС: Х10= an*qn +an-1*qn-1 + ….+a1*q1+ a0*q0 +a-1*q-1 +………+ a-m*q-m , (6) где an,an-1, ….a1,a0- цифры целой части исходного числа; a-1,… a-m- цифры дробной части исходного числа; q- основание исходной системы; n, m – количество целых и дробных разрядов. 2.1. Воспользовавшись правилом, приведённым в п.2 и формулой 6 перевести в десятичную СС 2.1.1. полученное в п.1.2.1 восьмеричное число с основанием q=8 (пример 4 расчётной схемы); 2.1.2. полученное в п.1.2.2 двоичное число с основанием q=2 (пример 5 расчётной схемы); 2.1.3. полученное в п.1.2.3 шестнадцатеричное число с основанием q=16 (пример 6 расчётной схемы).
Правило перевода: при переводе восьмеричного числа, основание qкоторого представляет собой целую степень числа 2, т.е. q=2n (8=23) , в двоичную отдельные цифры заменяют их двоичными эквивалентами. Здесь лишь следует помнить, что каждая цифра в новой системе должна содержать число разрядов, равное n (n=3). Например, 2158=?2 Решение: 28=0102; 18=0012; 58=1012 2158=0100011012 3.1. Перевести полученное в п. 1.2.1 восьмеричное число с основанием q=8 в двоичную СС (пример 7 расчётной схемы); 4. Перевести полученное дробное двоичное число в шестнадцатеричную СС Правило перевода: при переводе двоичное число разбивают на группы по n разрядов (n=4) и заменяют цифровыми эквивалентами новой шестнадцатеричной системы (табл.7.1, с. 119) [1]. Здесь следует помнить, что при переводе смешанных чисел разбиение на группы для целых частей осуществляется влево от запятой, а для дробных – вправо. Если окажется, что некоторых позиций не хватает, их заменяют нулями. Например, 1111011100012=?16 Решение: 00012=116; 01112=716; 11112=F16 1111011100012=F7116
Тема 1.2. Арифметические операции с кодированными числами Задачи 31-60 Условие: С заданными значениями десятичных чисел В10, Y10, Z10, А10 (см. таблицу 3) выполнить арифметические операции В2+ Z2, В2*Z2, [Y2+ Z2]обр, [В2+А2]обр, [Y2+ A2]доп Таблица 3 Исходные данные для решения задач 31-60
Методические указания к решению задач № 31-60 Основное применение в цифровых устройствах (ЦУ) нашла двоичная система счисления. Это связано с простой реализацией элементов с двумя различными состояниями и удобством выполнения арифметических преобразований. Для представления двоичных чисел в ЦУ применяют прямой, дополнительный и обратный коды. Прямой код. Число Х в прямом коде [x]пр представляется в виде: [x]пр =0ε1 ε2 …… εn , если х≥0, [x]пр =1ε1 ε2 …… εn , если х<0, (7) где εi – двоичная цифра 0 или 1; n- число разрядов. Обратный код. Число Х в обратном коде [x]обр представляется в виде: [x]обр =[x]пр =0ε1 ε2 …… εn , если х≥0, [x]обр =1ε1* ε2* …… εn* , если х<0, (8) где εi* – двоичная цифра, образуемая заменой исходного значения на противоположное (дополнение до единицы); n- число разрядов. Дополнительный код. Число Х в дополнительном коде [x]доп представляется в виде: [x]длп =[x]пр =0ε1 ε2 …… εn , если х≥0, [x]доп =[x]обр +ε1/ ε2/ …… εn-1/1 , если х<0, (9) где εi/ =0; n- число разрядов. Выполнение арифметических операций в двоичной СС основывается на правилах:
Вместо операции вычитания в ЭВМ выполняется операция сложения уменьшаемого с вычитаемым противоположного знака (например, в дополнительном коде). В процессе выполнения операции деления операция вычитания делителя заменяется операцией сложения с делителем изменённого знака. Порядок решения
Например, В2 =1011, тогда [В2]обр =1011 А2=-1101, тогда [А2]обр =10010
Например, В2 =1011, тогда [В2]доп =1011 А2=-1101, тогда [А2]доп =[А2]обр +00001=10010+00001=10011
Для этого необходимо сложить эти числа в столбик, воспользовавшись вышеприведённым правилом 1. Сложение чисел осуществляется поразрядно, начиная с младшего разряда. В каждом разряде производится сложение двух цифр слагаемых или этих цифр и единицы переноса из предыдущего разряда. В результате возможно появление единицы переноса в старший разряд. Например, В2 =1011, Z2=111011 Решение: +111011 1011 Ответ: 1000110
Для этого необходимо умножить одно число (множитель) на другое (множимое) в столбик. Причём множимое последовательно умножают на все разряды множителя, воспользовавшись вышеприведённым правилом 2, получая частичные произведения, каждое из которых сдвигается на один разряд влево. После чего находят сумму получившихся частичных произведений, используя правило 1. Например, В2 =1011, Z2=111011 Решение: х111011 1011 +111011 +111011 +000000 111011____ Ответ: 1010001001
Для этого необходимо произвести следующие действия:
В данном случае суммируются два числа, одно из которых отрицательное (Y10) и больше (по модулю), чем положительное (Z10). Поэтому результатом суммирования будет отрицательное число. Например, [Z2]обр =1011 (Z10=11, Z2=1011) [Y2]обр =10010 (Y10=-13, Y2=-1101) Решение: +1011 10010 11101 Ответ: -00102=-210
Для этого необходимо произвести следующие действия:
В данном случае суммируются два числа, одно из которых отрицательное (А10) и меньшее (по модулю), чем положительное (В10). Поэтому результатом суммирования будет положительное число. Например, [В2]обр =110110 (В10=54, В2=110110) [А2]обр =100000 (А10=-31, А2=-11111) Решение: +110110 100000 +1010110 1 010111 Ответ: 101112=2310
Для этого необходимо произвести следующие действия:
В данном случае суммируются два отрицательных числа. Поэтому результатом суммирования будет отрицательное число. Например, [Y 2]доп =101001 (Y 10=-23, Y 2=-10111) [А2]доп =100001 (А10=-31, А2=-11111) Решение: +101001 100001 - 1001010 1 001001 Ответ: -1101102=-5410 Раздел 2. Логические основы цифровой схемотехники | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
