Python_практикум. Методическое пособие для практических и лабораторных работ для студентов направлений подготовки

• Название: Методическое пособие для практических и лабораторных работ для студентов направлений подготовки
• Дата: 02.06.2022
• Размер: 267 Kb.
• Имя файла: Python_практикум.doc
• Тип: Методическое пособие; #565005
• страница: 4 из 7

Операторы break и continue

При работе с циклами используются операторы break и continue. Оператор break предназначен для досрочного прерывания работы цикла while.

Пример.

a = 0

while a >= 0 :

if a == 7 :

break

a += 1

print ( "A" )
В приведенном выше коде, выход из цикла произойдет при достижении переменной a значения 7. Если бы не было этого условия, то цикл выполнялся бы бесконечно.

Оператор continue запускает цикл заново, при этом код, расположенный после данного оператора, не выполняется при текущей итерации.

Пример.

a = - 1

while a < 10 :

a += 1

if a == 7 :

continue

print ( "A" )
При запуске данного кода будут напечатаны 10 чисел, несмотря на то, что всего будет выполнено 11 проходов цикла, число 7 будет пропущено.

Оператор цикла for

Оператор for выполняет указанный набор инструкций заданное количество раз, которое определяется количеством элементов в диапазоне range:
range(a) означает диапазон от 0 до a-1 включительно;
range(a,b) означает диапазон от a до b-1 включительно;
range(a,b,c) означает диапазон от a до b-1 включительно с шагом c.

Пример.

for i in range ( 5 ):

print ( "Hello" )
В результате “ Hello ” будет выведено пять раз.

Внутри тела цикла можно использовать операторы break и continue, принцип работы их точно такой же, как и в операторе while.
Задания

1. 
   Напишите программу, которая 10 раз напечатает ваше имя.
   
2. 
   Напишите программу, которая будет запрашивать у пользователя числовой пароль до тех пор, пока он не введет его правильно. Пароль придумайте сами.
   
3. 
   Напишите программу, которая будет запрашивать у пользователя числовой пароль до тех пор, пока он не введет его правильно, но не более 5 раз. После пяти попыток программа должна завершить работу с сообщением об отказе.
   
4. 
   Запрограммируйте двумя способами вычисление суммы квадратов чисел от 1 до n (n вводится пользователем).
   
5. 
   Напишите программу поиска наибольшего из n введенных пользователем чисел. Сначала вводится число n, затем n чисел.
   
6. 
   Имеется последовательность 1, 1/2, 1/3, 1/4 и т. д. Напишите программу, которая определяет, сколько членов последовательности нужно сложить, чтобы сумма превысила заданное число, которое вводится пользователем.
   
7. 
   Вычислите двумя методами площадь криволинейной фигуры, соответствующей вашему номеру варианта.
   

Приближенное вычисление площадей

Программирование циклов мы рассмотрим на примере реализации методов приближенных вычислений. Пусть нам требуется найти приближенно площадь фигуры, ограниченной осью абсцисс и кривой на промежутке [2;5] (рис. 4.1).

Вариант 1: метод прямоугольников.

Идея метода: криволинейная фигура разбивается на много узких полосок, каждая полоска заменяется прямоугольником. Площадь фигуры приближенно равна сумме площадей этих прямоугольников.

Для решения задачи разобьем фигуру, скажем, на 100 полосок. Каждую из них заменим прямоугольником шириной, равной 1/100 отрезка [2;5],и высотой, равной значению функции 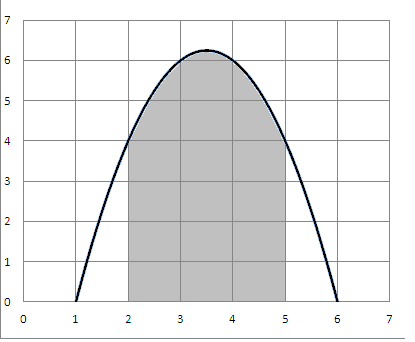в средней точке разбиения¹. Площадь каждого из них равна произведению ширины на высоту.


Рис. 4.1.
Фрагмент программы, предназначенный для вычисления площади, может выглядеть примерно так:
w = (b – a)/100 #вычисляем ширину полоски

s = 0 #переменная для накопления площади

x = a + w/2 #начальное значение х

while x < b: #пока не дошли до конца отрезка

s += w*(-x**2 + 7*x - 6)

#добавляем к s площадь очередной полоски

x += w #переходим к следующей полоске
Для того чтобы программа была завершенной, нужно предусмотреть выдачу результата. Завершите и отладьте программу. Полученный результат сравните с точным ответом, вычисленным с помощью интеграла.
Вариант 2: метод Монте-Карло¹.

Идея метода – смоделировать случайное «бросание» большого количества точек в прямоугольник, содержащий криволинейную фигуру. При этом отношение числа точек, попавших внутрь фигуры, к общему числу точек будет приближенно равно отношению площади фигуры к площади прямоугольника. Интуитивно понятно, что чем больше точек, тем точнее результат, однако оценить точность при использовании метода Монте-Карло не удается.

Прямоугольник, содержащий фигуру, имеет размеры 3х7 (на рис. 4.1 видно, что высота фигуры не превосходит семи, а ширина – трех).

Смоделируем бросание, например, 10000 точек и подсчитаем, сколько из них попали внутрь интересующей нас фигуры. Ее площадь будет вычисляться из пропорции


Фрагмент программы, предназначенный для вычисления площади, может выглядеть примерно так:
import random

k = 0

for i in range(10000):

x = random.uniform(a,b) #случайное от a до b

y = random.uniform(0,7)

#случайное от 0 до максимума функции

if y < -x**2 + 7*x -6:

#случайная точка попала под кривую

k += 1

s = 7 * (b - a) * k / 10000

# площадь прямоугольника умножаем на число

# попавших в фигуру точек

# и делим на общее число точек
Завершите программу, добавив вывод вычисленной площади. Проверьте ответ, сравнив его с результатом предыдущей программы. Понятно, что точного совпадения не будет, более того, каждый запуск программы будет давать результат, отличный от предыдущего, т.к. зависит от случайности.
Задания

1. 
   Измените обе программы таким образом, чтобы они позволяли вычислять площадь фигуры на произвольном отрезке [a;b]. Границы его должны вводиться пользователем.
   
2. 
   Добавьте возможность вычисления двумя способами площади другой фигуры (уточните у преподавателя, какой именно). Проверьте свой результат с помощью вычисления определенного интеграла.