ЗАДАЧА 5
Побудувати надійний інтервал для оцінки з надійністю 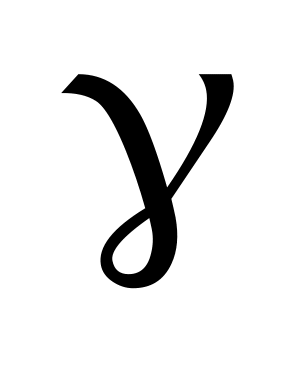 невідомого середнього квадратичного відхилення невідомого середнього квадратичного відхилення 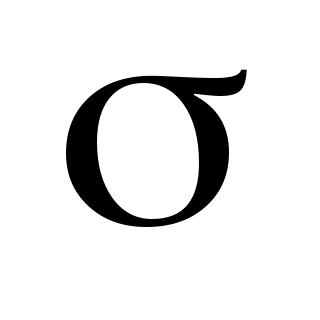 нормально розподіленої генеральної сукупності Х, якщо відомі виправлене середнє квадратичне відхилення нормально розподіленої генеральної сукупності Х, якщо відомі виправлене середнє квадратичне відхилення 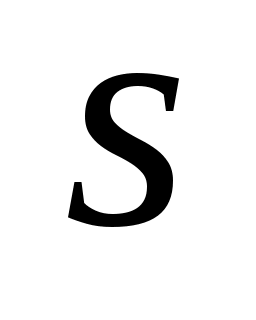 і об’єм вибірки і об’єм вибірки 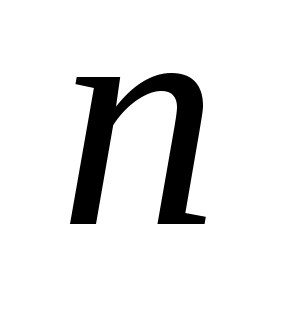 . .
№
|
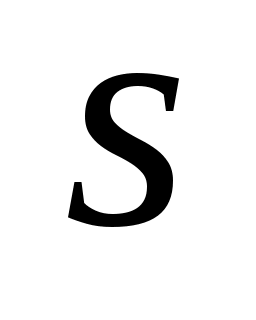
|
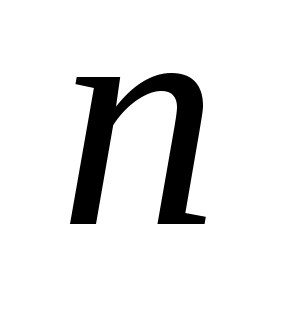
|
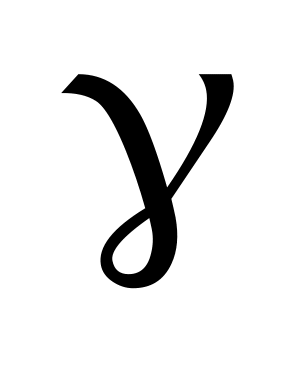
|
|
№
|
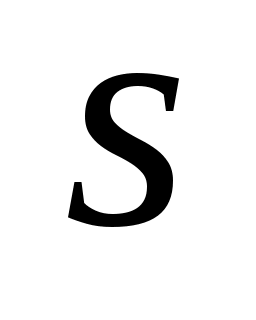
|
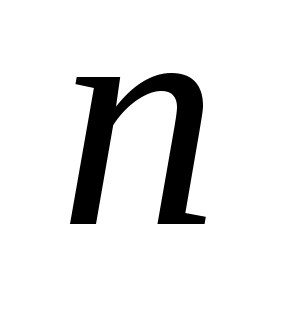
|
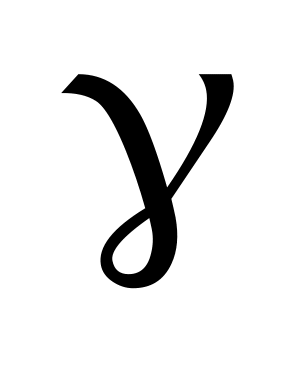
|
5.1
5.2
5.3
5.4
5.5
5.6
|
0,5
1,5
4,5
0,8
2,4
2,3
|
20
10
6
30
9
12
|
0,999
0,99
0,95
0,999
0,99
0,95
|
|
5.7
5.8
5.9
5.10
5.11
5.12
|
0,7
0,6
1,3
0,9
1,8
0,7
|
25
18
15
35
20
16
|
0,999
0,99
0,95
0,999
0,99
0,95
|
№
|
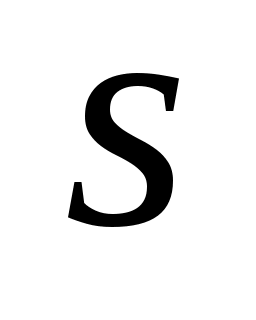
|
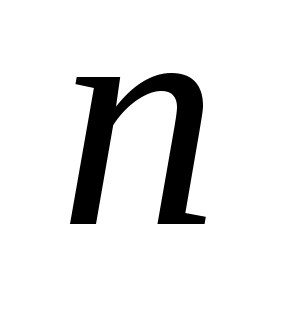
|
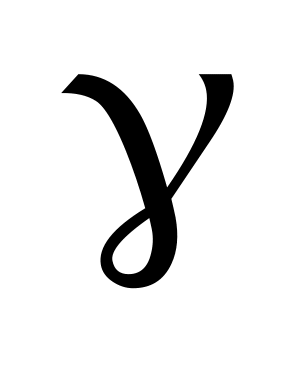
|
|
№
|
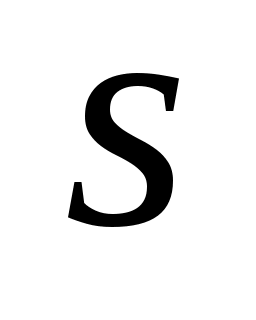
|
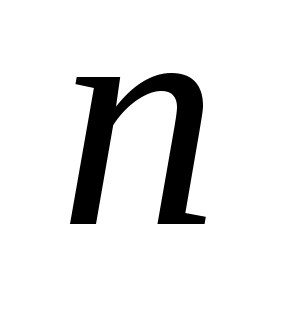
|
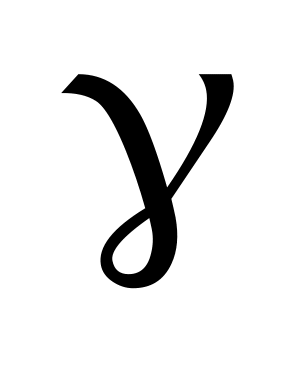
|
5.13
5.14
5.15
5.16
5.17
5.18
5.19
5.20
5.21
|
1,0
2,1
1,5
1,1
0,8
0,6
0,6
1,0
1,1
|
40
25
18
45
30
20
50
35
25
|
0,999
0,99
0,95
0,999
0,99
0,95
0,999
0,99
0,95
|
|
5.22
5.23
5.24
5.25
5.26
5.27
5.28
5.29
5.30
|
2,5
1,4
0,9
1,8
2,8
1,5
2,0
1,9
0,5
|
16
40
30
15
8
11
14
45
35
|
0,999
0,99
0,95
0,999
0,99
0,95
0,999
0,99
0,95
|
ЗАДАЧА 6
Знайти вибіркове рівняння прямої лінії регресії 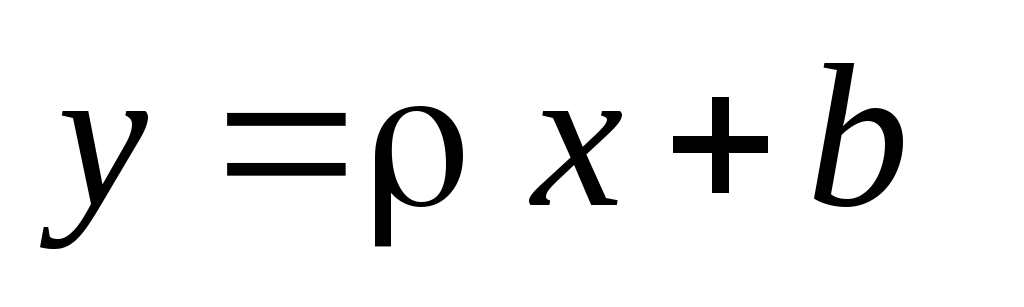 за даними п’яти спостережень (хі; yі) над величинами X та Y. Зробити малюнок, на якому вказати експериментальні дані та побудувати пряму регресії. за даними п’яти спостережень (хі; yі) над величинами X та Y. Зробити малюнок, на якому вказати експериментальні дані та побудувати пряму регресії.
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6.20
6.21
6.22
6.23
6.24
6.25
6.26
6.27
6.28
6.29
6.30
|
(1; 4,9)
(2; 3,5)
(1; 0,9) (1; 4,7) (0; 3,5)
(1; 1,5)
(1; 4,5)
(2; 5,3)
(0; 1,2)
(1; 4,2)
(2; 4,9)
(0; 3,7)
(2; 1,5)
(1; 2,9)
(1; 4,1)
(0; 4,3)
(1; 2,5)
(1; 3,9)
(0; 3,5)
(1; 2,3)
(1; 3,7)
(2; 5,5)
(2; 4,5)
(1; 3,5)
(1; 3,3)
(1; 2,5)
(2; 2,5)
(1; 0,9)
(1; 3,1)
(0; 0,8)
|
(2; 5,9)
(4; 5,8)
(3; 2,9)
(2; 5,7)
(2; 3,8)
(3; 4,5)
(2; 5,5)
(3; 6,3)
(1; 2,1)
(2; 5,2)
(3; 5,7)
(1; 4,2)
(3; 2,8)
(2; 3,9)
(2; 4,9)
(1; 2,5)
(3; 4,8)
(2; 4,8)
(2; 6,1)
(2; 2,5)
(2; 4,7)
(3; 6,5)
(4; 7,1)
(2; 4,5)
(2; 4,3)
(3; 1,8)
(4; 2,8)
(2; 3,3)
(2; 2,6)
(2; 2,5)
|
(3; 4,4)
(6; 7,1)
(4; 2,5)
(3; 4,2)
(4; 1,8)
(4; 4,1)
(3; 3,9)
(4; 4,9)
(2; 1,5)
(3; 3,7)
(4; 4,3)
(2; 2,7)
(4; 2,4)
(3; 2,3)
(3; 3,6)
(3; 3,1)
(5; 5,9)
(3; 3,4)
(4; 6,9)
(3; 4,5)
(3; 3,2)
(4; 5,1)
(6; 8,1)
(3; 2,9)
(3; 2,8)
(5; 3,1)
(6; 5,1)
(3; 4,5)
(3; 3,4)
(4; 2,6)
|
(4; 3,4)
(8; 6,1)
(6; 5,1)
(4; 2,2)
(6; 1,5)
(5; 6,4)
(4; 2,1)
(5; 2,9)
(3; 2,9)
(4; 1,7)
(5; 2,4)
(3; 3,3)
(6; 4,8)
(4; 0,8)
(4; 1,9)
(5; 2,1)
(7; 4,9)
(4; 1,4)
(6; 6,5)
(4; 4,1)
(4; 1,4)
(5; 3,2)
(8; 7,5)
(4; 1,5)
(4; 1,1)
(7; 4,9)
(7; 3,9)
(4; 4,1)
(4; 2,5)
(6; 4,8)
|
(5; 2,9)
(10; 7,5)
(7; 4)
(5; 2,7)
(7; 0,4)
(6; 6,8)
(5; 2,5)
(6; 3,3)
(4; 2,5)
(5; 2,2)
(6; 2,9)
(4; 1,5)
(7; 3,8)
(5; 1,3)
(5; 2,1)
(7; 0,3)
(9;6,5)
(5; 1,9)
(8; 7,5)
(5; 5,5)
(5; 1,7)
(6; 3,6)
(10;8,5)
(5; 1,8)
(5; 1,4)
(9; 6,1)
(8; 5,3)
(5; 6,2)
(5; 0,9)
(8; 3,9)
|
ЗАДАЧА 7
Використовуючи критерій Пірсона, при рівні значущості 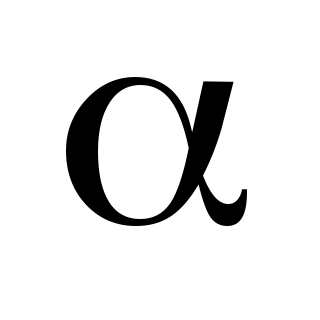 перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х з статистичними даними, які подані у вигляді інтервального варіаційного ряду (в першому рядку вказано часткові інтервали перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х з статистичними даними, які подані у вигляді інтервального варіаційного ряду (в першому рядку вказано часткові інтервали  , в другому – відповідні їм частоти , в другому – відповідні їм частоти  ). ).
7.1 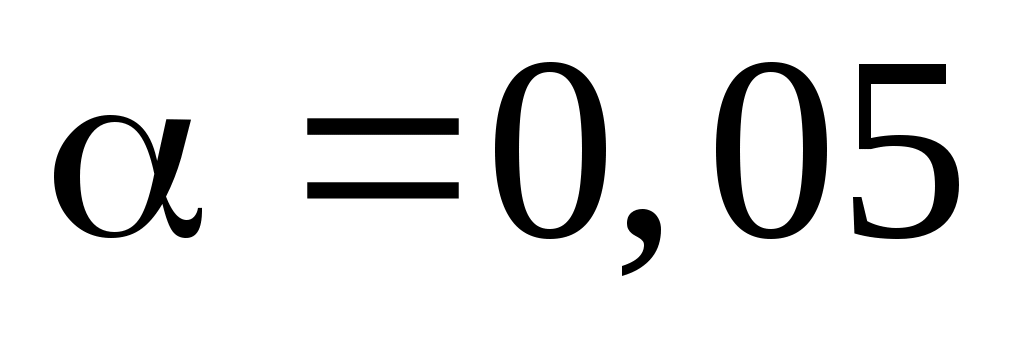 ; ;

|
2-12
|
12-22
|
22-32
|
32-42
|
42-52
|
52-62
|
62-72
|

|
7
|
8
|
15
|
36
|
15
|
11
|
8
|
7.2 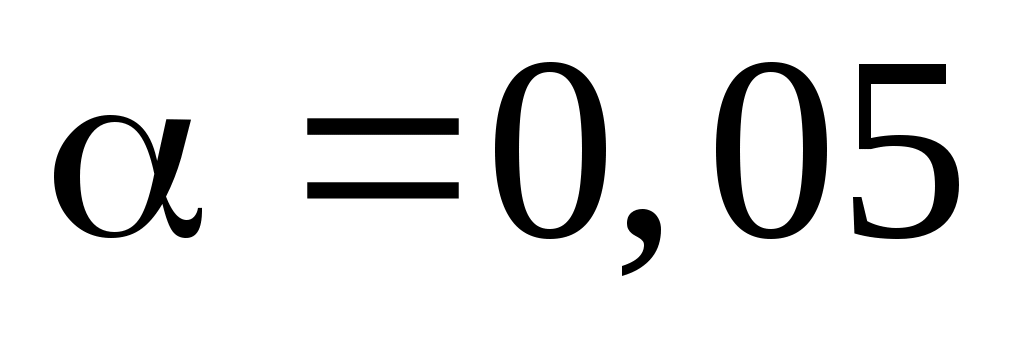 ; ;

|
1,5-3,5
|
3,5-5,5
|
5,5-7,5
|
7,5-9,5
|
9,5-11,5
|
11,5-13,5
|
13,5-15,5
|

|
4
|
18
|
12
|
35
|
15
|
10
|
6
|
7.3 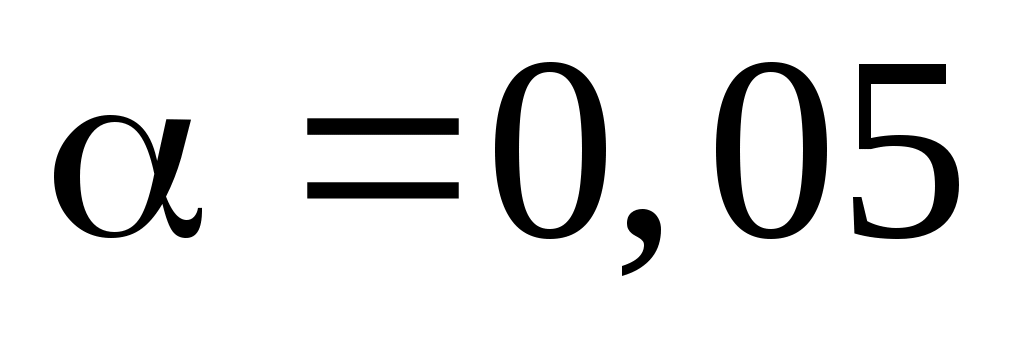 ; ;

|
1-6
|
6-11
|
11-16
|
16-21
|
21-26
|
26-31
|
31-36
|

|
6
|
12
|
16
|
40
|
13
|
8
|
5
|
7.4 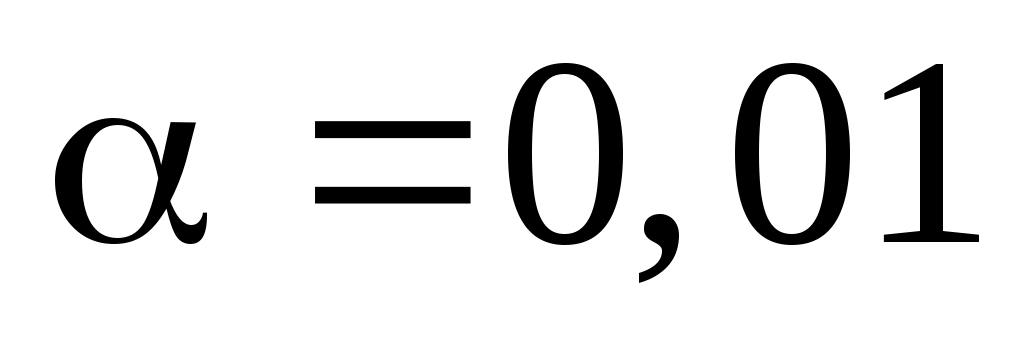 ; ;

|
3,0-3,6
|
3,6-4,2
|
4,2-4,8
|
4,8-5,4
|
5,4-6,0
|
6,0-6,6
|
6,6-7,2
|

|
6
|
8
|
31
|
43
|
22
|
15
|
5
|
7.5 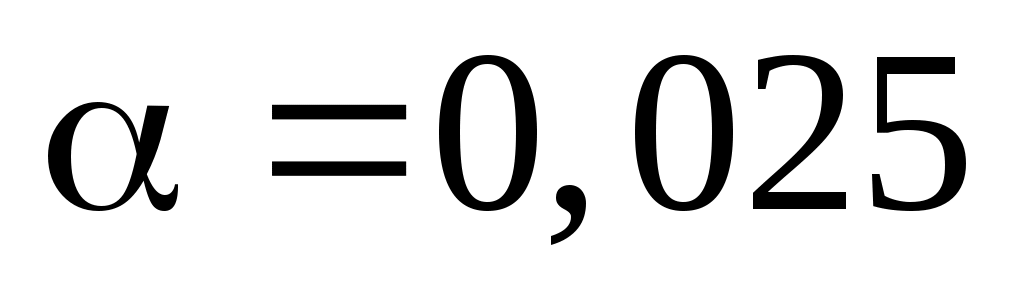 ; ;

|
0-2,2
|
2,2-4,4
|
4,4-6,6
|
6,6-8,8
|
8,8-11,0
|
11,0-13,2
|
13,2-15,4
|
ni
|
14
|
18
|
32
|
70
|
20
|
36
|
10
|
7.6 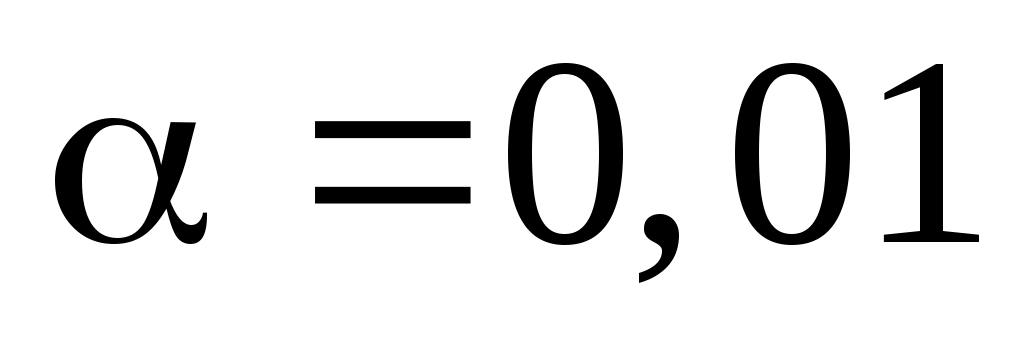 ; ;

|
–4 - 0
|
0-4
|
4-8
|
8-12
|
12-16
|
16-20
|
20-24
|

|
8
|
16
|
40
|
72
|
36
|
18
|
10
|
7.7 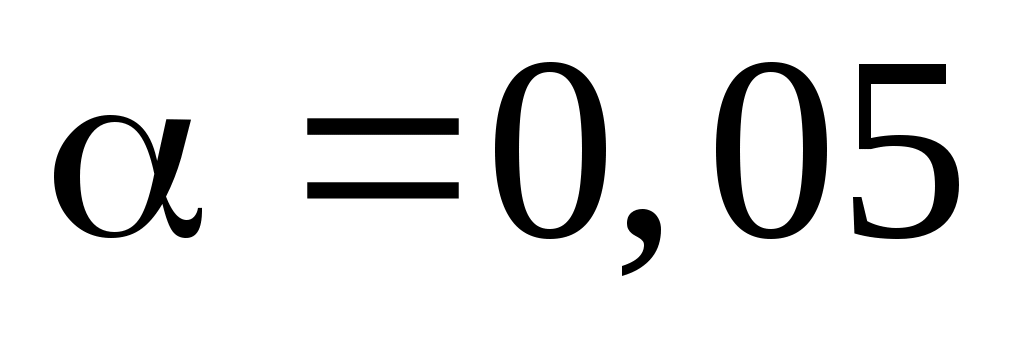 ; ;

|
2-7
|
7-12
|
12-17
|
17-22
|
22-27
|
27-32
|
32-37
|

|
10
|
26
|
25
|
30
|
26
|
21
|
12
|
7.8 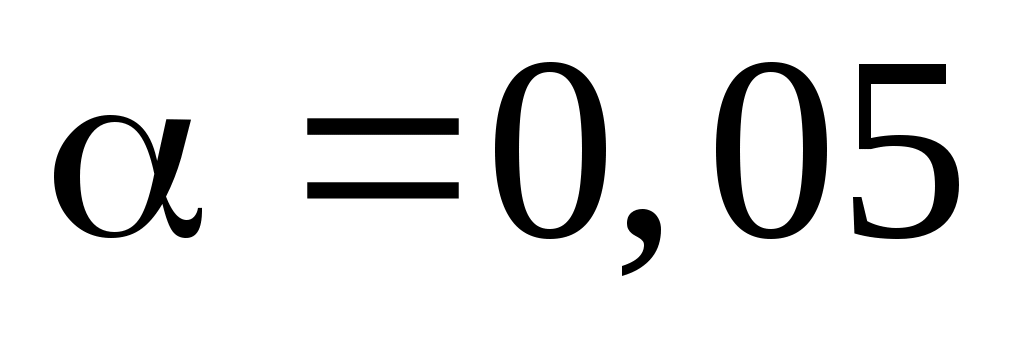 ; ;

|
–10- –5
|
–5-0
|
0-5
|
5-10
|
10-15
|
15-20
|
20-25
|

|
14
|
18
|
32
|
70
|
36
|
20
|
10
|
7.9 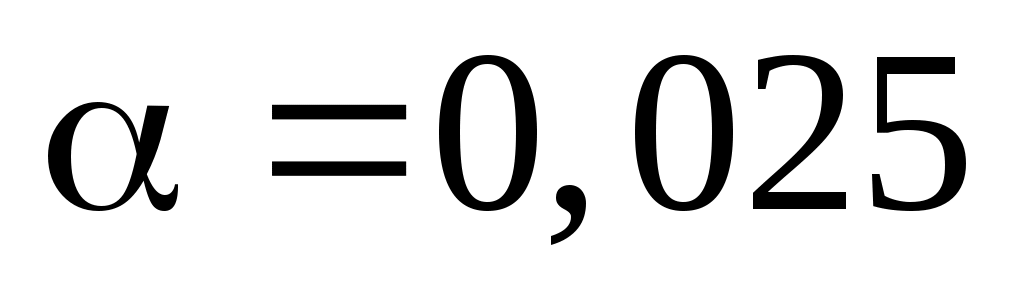 ; ;

|
4-6
|
6-8
|
8-10
|
10-12
|
12-14
|
14-16
|
16-18
|

|
12
|
14
|
38
|
15
|
10
|
7
|
4
|
7.10 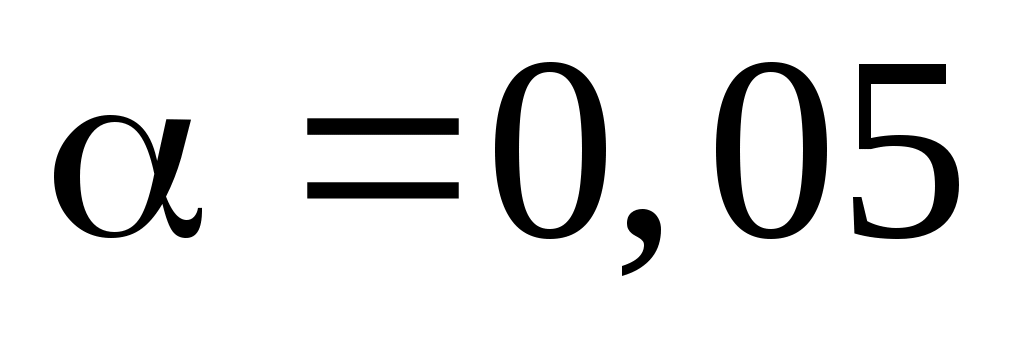 ; ;

|
0-10
|
10-20
|
20-30
|
30-40
|
40-50
|
50-60
|
60-70
|

|
10
|
27
|
55
|
70
|
20
|
13
|
5
|
7.11 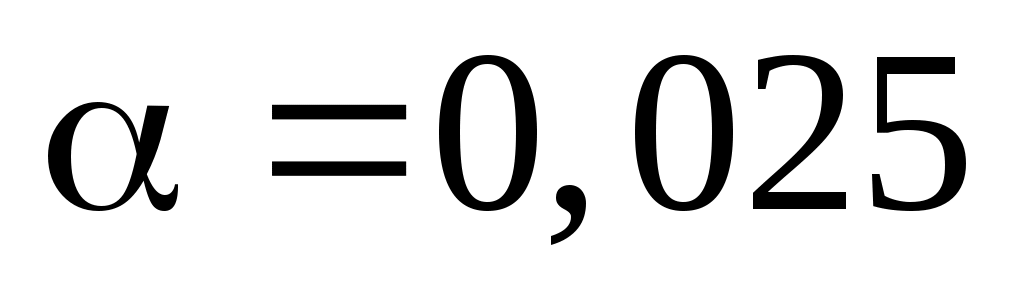 ; ;

|
1,8-2,8
|
2,8-3,8
|
3,8-4,8
|
4,8-5,8
|
5,8-6,8
|
6,8-7,8
|
7,8-8,8
|

|
5
|
15
|
23
|
27
|
19
|
6
|
5
|
7.12 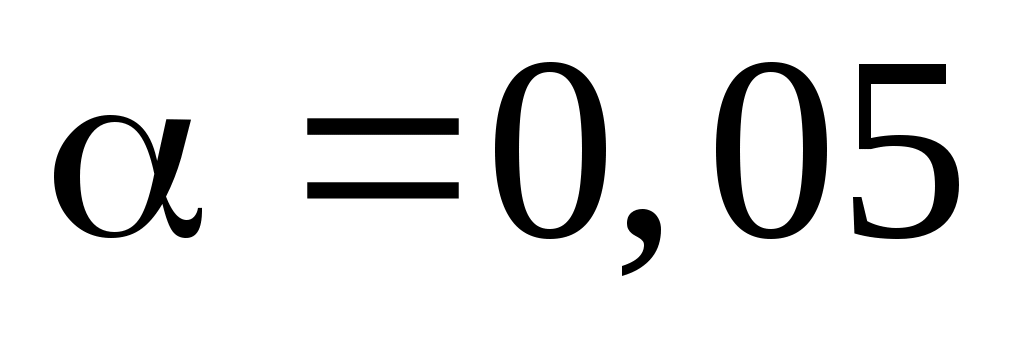 ; ;

|
10-13
|
13-16
|
16-19
|
19-22
|
22-25
|
25-28
|
28-31
|

|
12
|
23
|
30
|
29
|
29
|
16
|
11
|
7.13 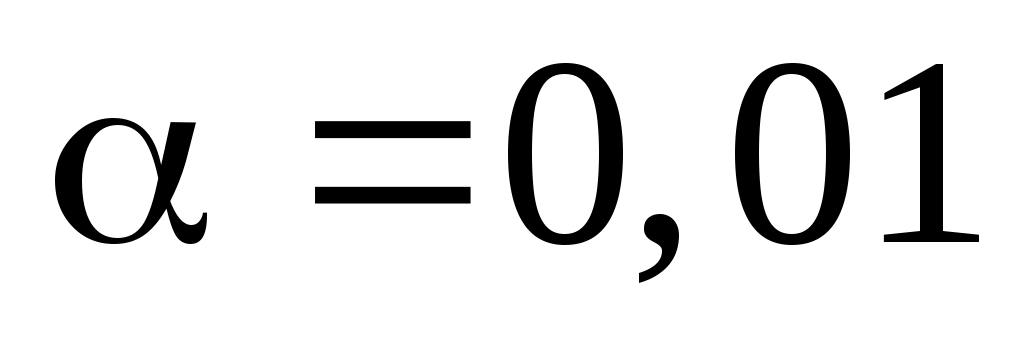 ; ;

|
1,2-5,2
|
5,2-9,2
|
9,2-13,2
|
13,2-17,2
|
17,2-21,2
|
21,2-25,2
|
25,2-29,2
|

|
8
|
28
|
32
|
66
|
36
|
20
|
10
|
7.14 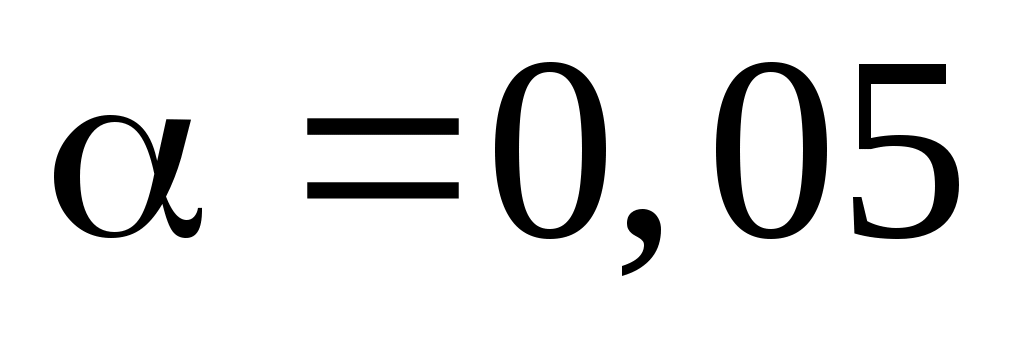 ; ;

|
1,5-4,5
|
4,5-7,5
|
7,5-10,5
|
10,5-13,5
|
13,5-16,5
|
16,5-19,5
|
19,5-22,5
|

|
5
|
12
|
34
|
50
|
28
|
14
|
7
|
7.15 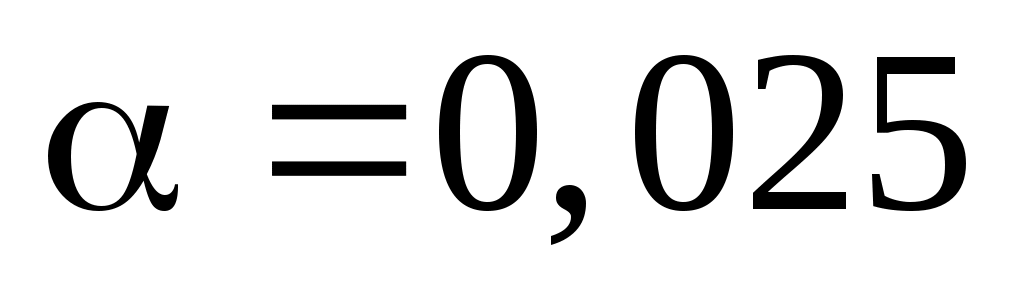 ; ;

|
10,5-12,5
|
12,514,5
|
14,5-16,5
|
16,5-18,5
|
18,5-20,5
|
20,5-22,5
|
22,5-24,5
|

|
15
|
25
|
32
|
50
|
12
|
10
|
6
|
7.16 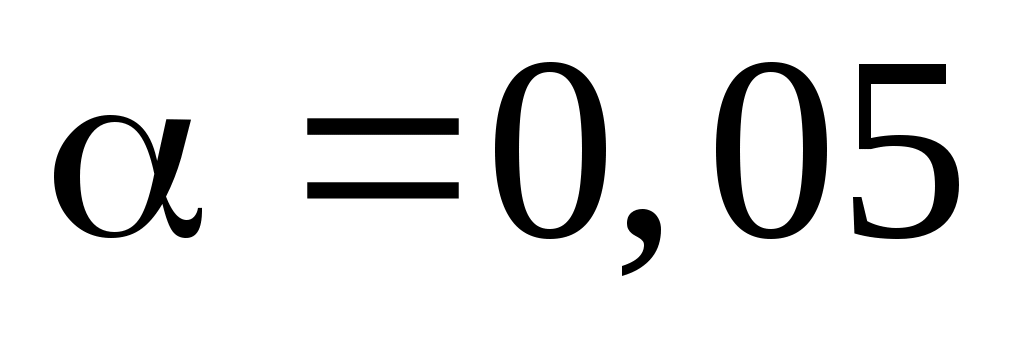 ; ;

|
10-16
|
16-22
|
22-28
|
28-34
|
34-40
|
40-46
|
46-52
|

|
9
|
24
|
34
|
48
|
20
|
9
|
6
|
7.17 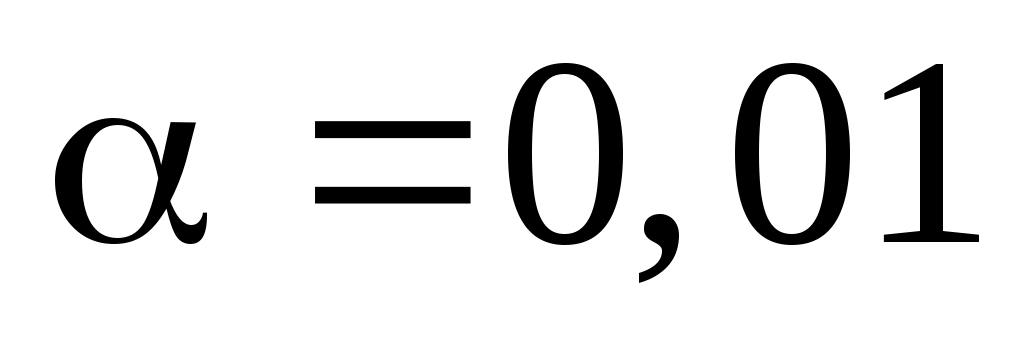 ; ;

|
2,0-3,5
|
3,5-5,0
|
5,0-6,5
|
6,5-8,0
|
8,0-9,5
|
9,5-11,0
|
11,0-12,5
|

|
5
|
16
|
21
|
42
|
32
|
8
|
6
|
7.18 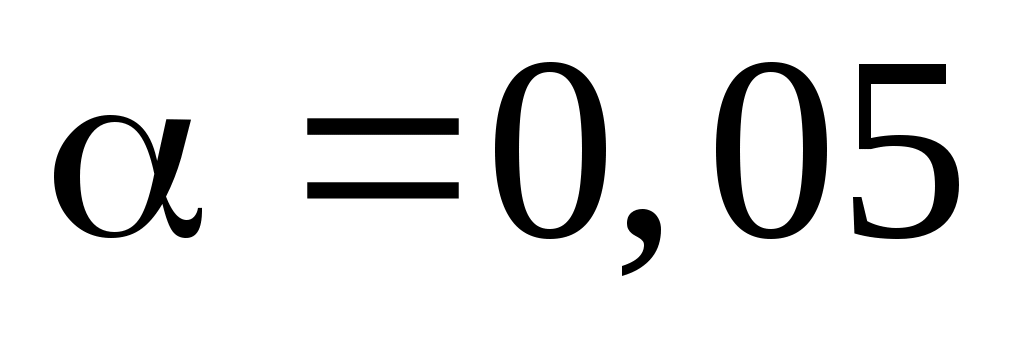 ; ;

|
9-11
|
11-13
|
13-15
|
15-17
|
17-19
|
19-21
|
21-23
|

|
6
|
8
|
15
|
32
|
18
|
14
|
7
|
7.19 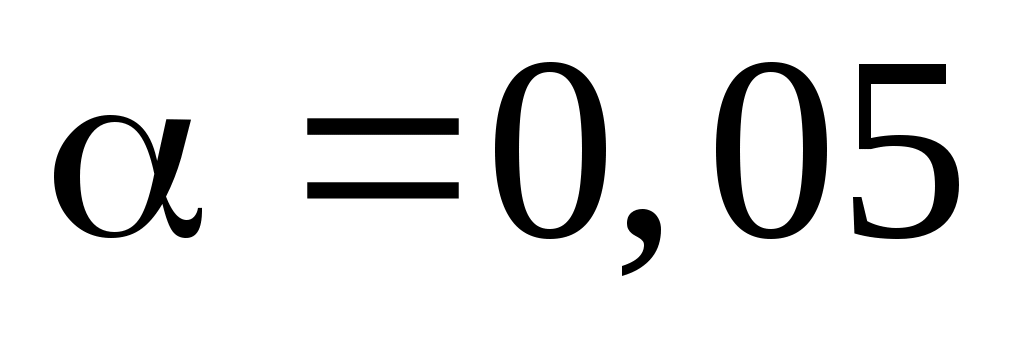 ; ;

|
0,5-5,5
|
5,5-10,5
|
10,5-15,5
|
15,5-20,5
|
20,5-25,5
|
25,5-30,5
|
30,5-35,5
|

|
13
|
20
|
30
|
60
|
35
|
30
|
12
|
7.20 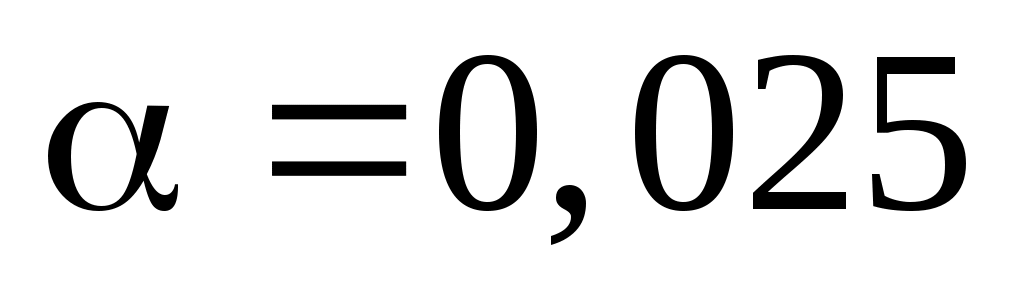 ; ;

|
12-15
|
15-18
|
16-21
|
21-24
|
24-27
|
27-30
|
30-33
|

|
10
|
13
|
20
|
65
|
55
|
24
|
13
|
7.21 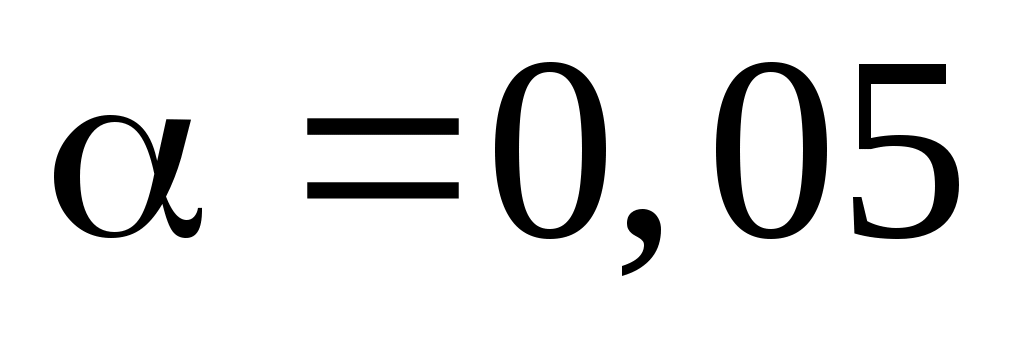 ; ;

|
2,6-6,6
|
6,6-10,6
|
10,6-14,6
|
14,6-18,6
|
18,6-22,6
|
22,6-26,6
|
26,6-30,6
|

|
6
|
10
|
17
|
45
|
35
|
22
|
15
|
7.22 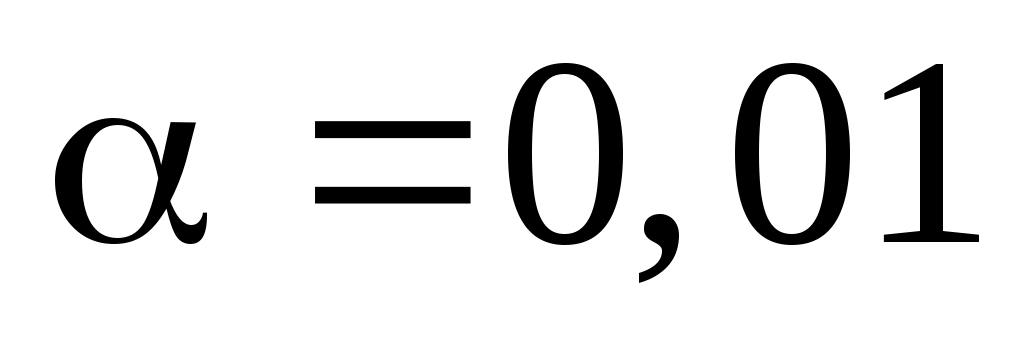 ; ;

|
2-8
|
8-14
|
14-20
|
20-26
|
26-32
|
32-38
|
38-44
|

|
12
|
18
|
22
|
38
|
24
|
20
|
16
|
7.23 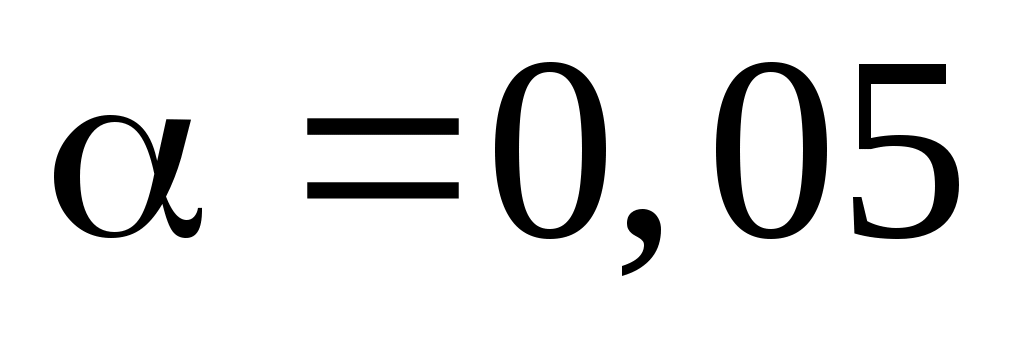 ; ;

|
3,5-7,5
|
7,5-11,5
|
11,5-15,5
|
15,5-19,5
|
19,5-23,5
|
23,5-27,5
|
27,5-31,5
|

|
5
|
10
|
23
|
45
|
36
|
22
|
9
|
7.24 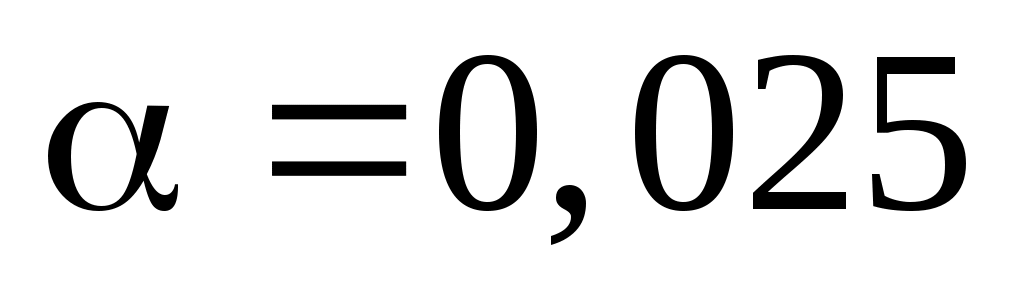 ; ;

|
8-18
|
18-28
|
28-38
|
38-48
|
48-58
|
58-68
|
68-78
|

|
15
|
20
|
26
|
40
|
26
|
16
|
7
|
7.25 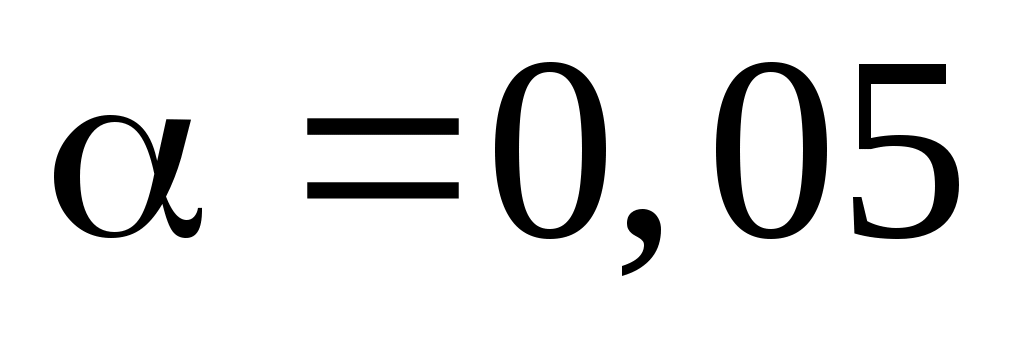 ; ;

|
–6-0
|
0-6
|
6-12
|
12-18
|
18-24
|
24-30
|
30-36
|

|
20
|
29
|
48
|
70
|
81
|
40
|
12
|
7.26 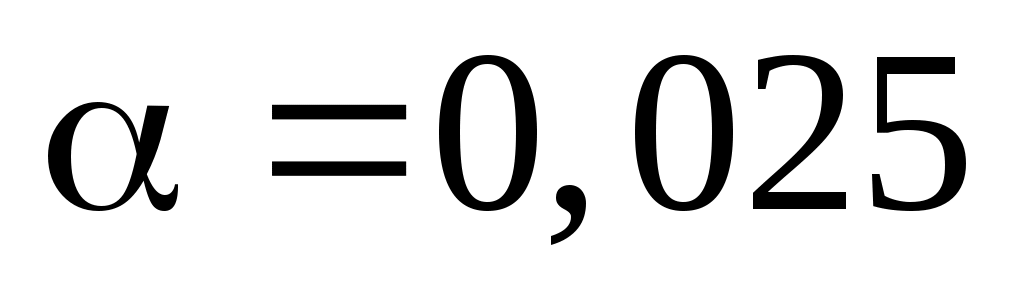 ; ;

|
–4-6
|
6-16
|
16-26
|
26-36
|
36-46
|
46-56
|
56-66
|

|
7
|
14
|
46
|
88
|
64
|
53
|
28
|
7.27 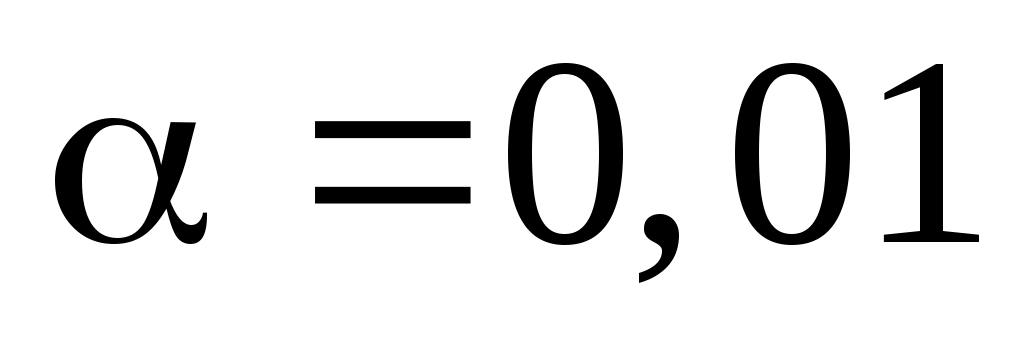 ; ;

|
–3-1
|
1-5
|
5-9
|
9-13
|
13-17
|
17-21
|
21-25
|

|
7
|
12
|
25
|
52
|
30
|
18
|
6
|
7.28 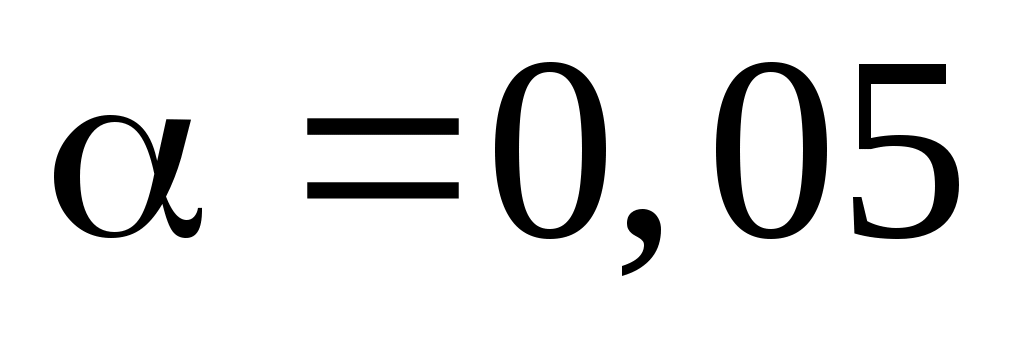 ; ;

|
0,5-2,5
|
2,5-4,5
|
4,5-6,5
|
6,5-8,5
|
8,5-10,5
|
10,5-12,5
|
12,5-14,5
|

|
12
|
24
|
38
|
64
|
34
|
18
|
10
|
7.29 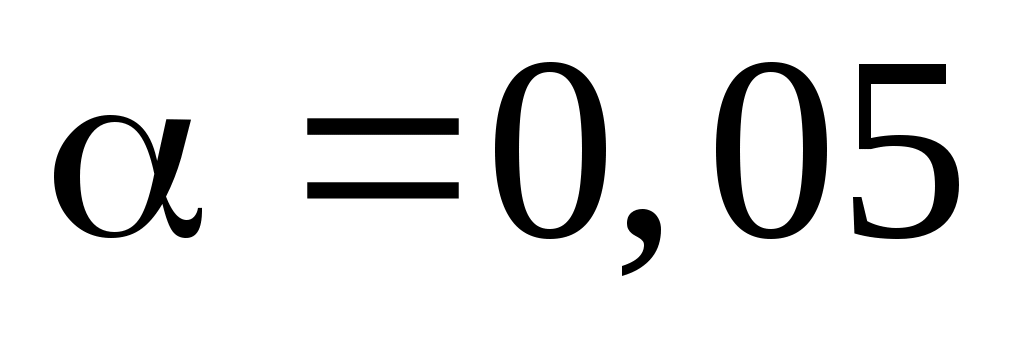 ; ;

|
–1,5-3,5
|
3,5-8,5
|
8,5-13,5
|
13,5-18,5
|
18,5-23,5
|
23,5-28,5
|
28,5-33,5
|

|
10
|
22
|
38
|
70
|
40
|
14
|
6
|
7.30 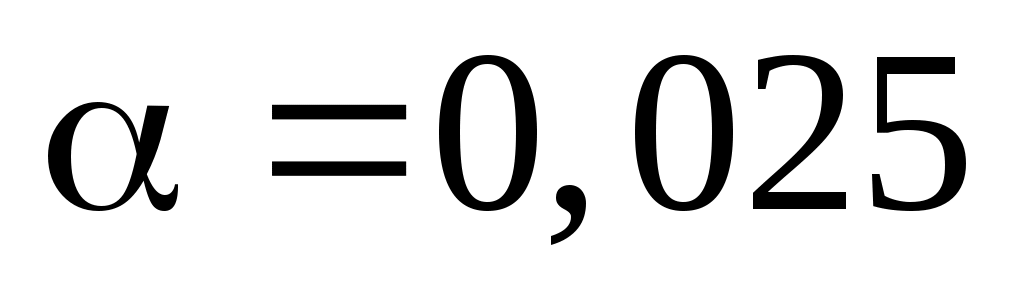 ; ;

|
–1,6-2,4
|
2,4-6,4
|
6,4-10,4
|
10,4-14,4
|
14,4-18,4
|
18,4-22,4
|
22,4-26,4
|

|
6
|
10
|
26
|
48
|
32
|
18
|
10
|
|
 Скачать 2.83 Mb.
Скачать 2.83 Mb.