Методичні вказівки для самостійної роботи студентів Частина 3 Теорія ймовірностей Математична статистика Житомир 2014
 Скачать 2.83 Mb. Скачать 2.83 Mb.
|
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧТеорія ймовірностейПриклад 1. В партії із 25 деталей є чотири браковані. Знайти ймовірність того, що серед взятих навмання для перевірки п’яти деталей буде дві браковані. Розв’язання. Розглянемо випадкову подію А – серед п’яти взятих навмання деталей дві браковані. За класичним визначенням ймовірності 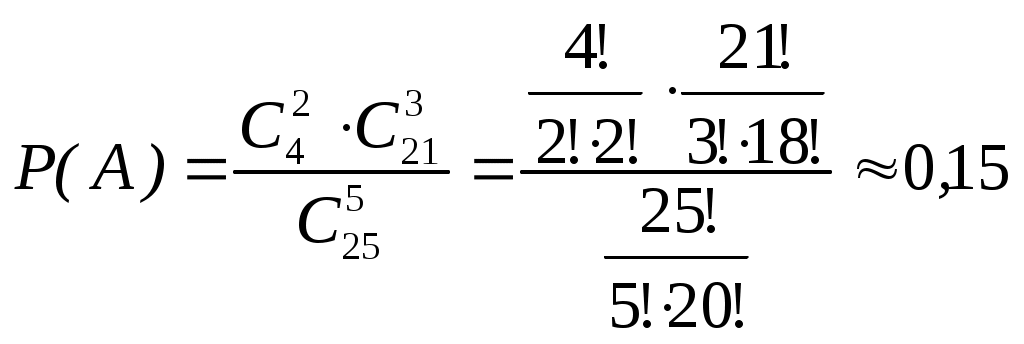 . .Приклад 2. Книги деякого чотиритомного видання розставляють навмання на полиці. Знайти ймовірність того, що всі чотири томи стоятимуть в порядку зростання їх номерів. Розв’язання. Загальне число елементарних подій дорівнює числу переставлень із чотирьох елементів, тобто n=4!=24. Події А сприяє лише одна елементарна подія (1,2,3,4), тобто m =1. Отже Приклад 3. В коробці 10 деталей, з яких 8 стандартних. З коробки навмання дістають три деталі. Знайти ймовірність того, що всі три деталі стандартні. Розв’язання. Подію А (всі три деталі стандартні) представимо як Приклад 4. Верстат–автомат штампує деталі. Ймовірність того, що за зміну не буде випущено жодної бракованої деталі, дорівнює 0,9. Знайти ймовірність того, що за три зміни не буде випущено жодної бракованої деталі. Розв’язання. Подію А (за три зміни не випущено жодної бракованої деталі) представимо, як Р(А)=Р(А1) Р(А2) Р(А3 )=0,9 0,9 0,9 = 0,729 . Приклад 5. На заводі перший цех виробляє 10%, другий – 70%, третій – 20% всіх деталей. В їх продукції браку, відповідно 9, 8, 7%. Знайти ймовірність того, що випадково вибрана деталь дефектна. Розв’язання. Нехай подія А – деталь дефектна. Висунемо гіпотези: Н1 – деталь виготовлена першим цехом; Н2 – деталь виготовлена другим цехом; Н3 – деталь виготовлена третім цехом. За умовою задачі, відповідні ймовірності Застосовуючи формулу повної ймовірності Приклад 6. На заводі перший цех виробляє 10%, другий – 70%, третій – 20% всіх деталей. В їх продукції браку, відповідно 9, 8, 7%. Випадково вибрана деталь виявилась дефектною. Знайти ймовірність того, що вона виготовлена другим цехом. Розв’язання. Нехай подія А – деталь дефектна. Висунемо гіпотези: Н1 – деталь виготовлена першим цехом; Н2 – деталь виготовлена другим цехом; Н3 – деталь виготовлена третім цехом. За умовою задачі, відповідні ймовірності Застосовуючи формулу Байєса 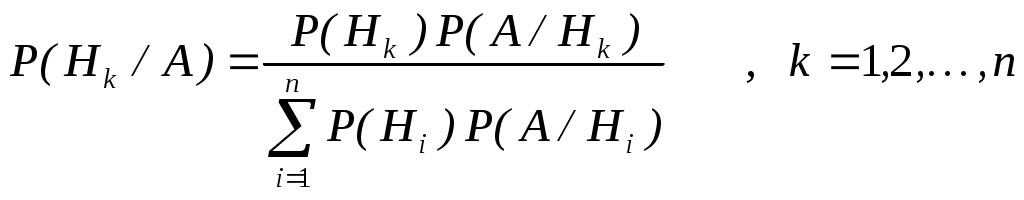 , отримаємо , отримаємо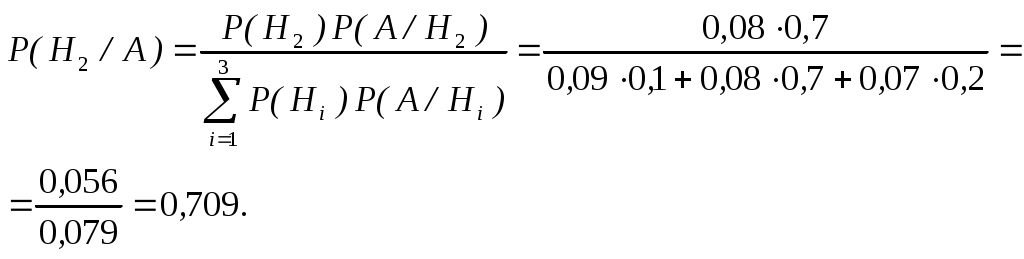 Приклад 7. Проводиться три незалежних випробування, в кожному з яких подія А відбувається з ймовірністю 0,4. Розглядається випадкова величина Х – число появ події А в трьох випробуваннях. Побудувати закон розподілу випадкової величини Х та знайти її математичне сподівання, дисперсію і середнє квадратичне відхилення. Розв’язання. Випадкова величина Х може набувати значень: Отримаємо: Закон розподілу випадкової величини має вигляд
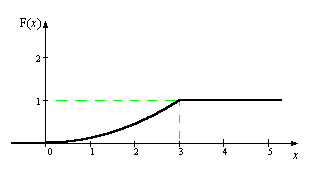
Обчислимо основні числові характеристики випадкової величини: 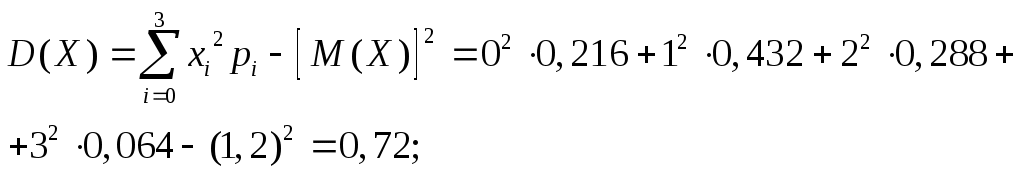 Приклад 8. Випадкова величина Х задана функцією розподілу 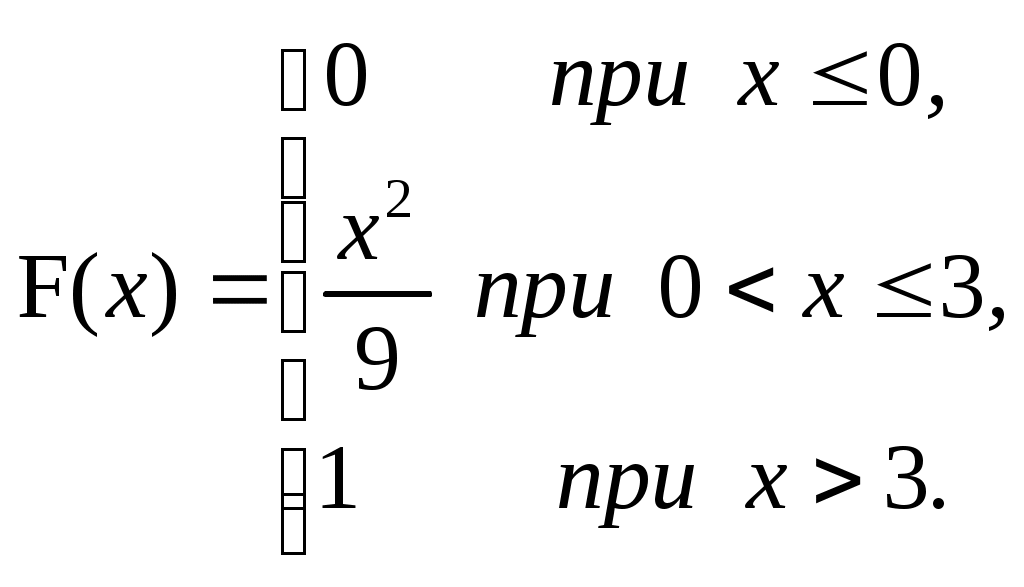 Знайти ймовірність попадання в інтервал (0;1), щільність розподілу, математичне сподівання, дисперсію та середнє квадратичне відхилення. Побудувати графіки функції розподілу та щільності розподілу. Розв’язання. Ймовірність попадання випадкової величини Х в інтервал (0;1): Оскільки щільність розподілу f(x)=F(x), то 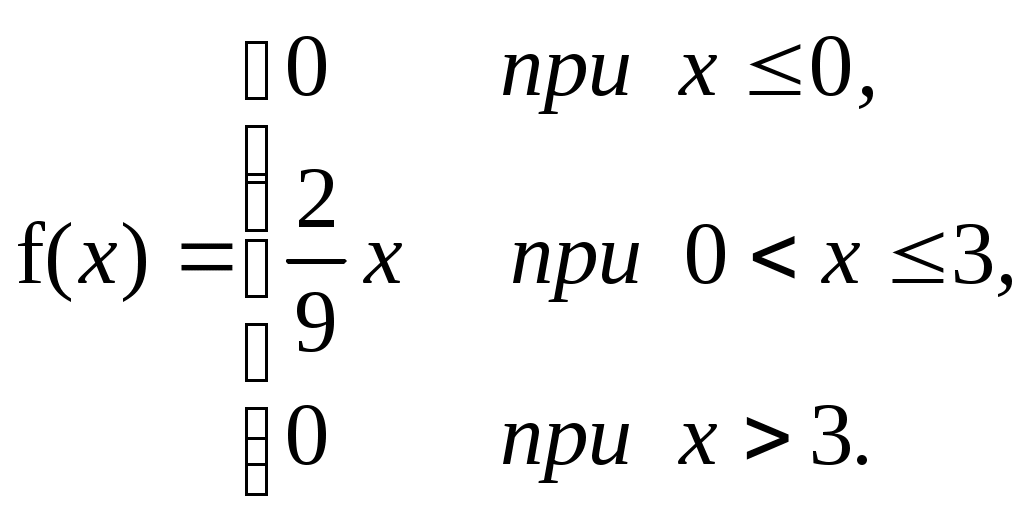 Знайдемо математичне сподівання випадкової величини Х: Визначимо дисперсію випадкової величини Х: Середнє квадратичне відхилення: Будуємо графік функції розподілу:
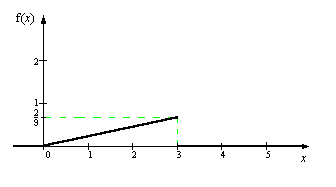
Будуємо графік щільності розподілу:
|