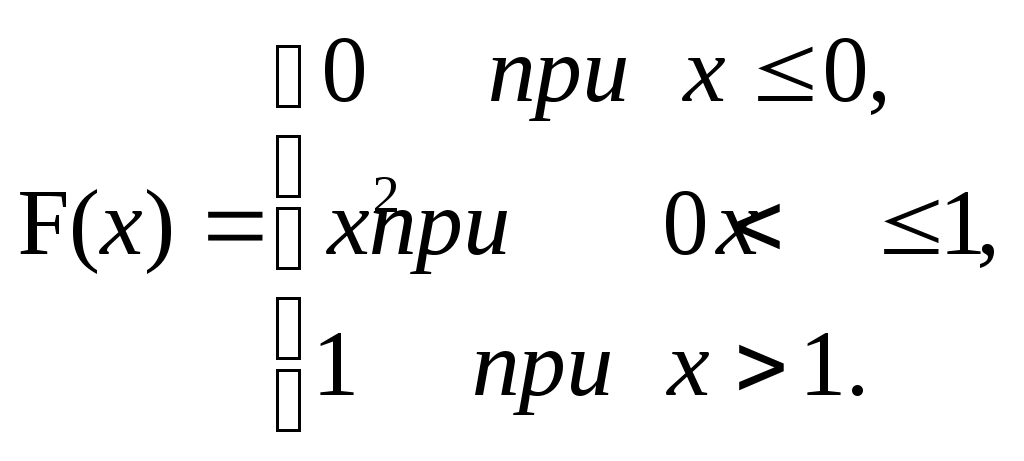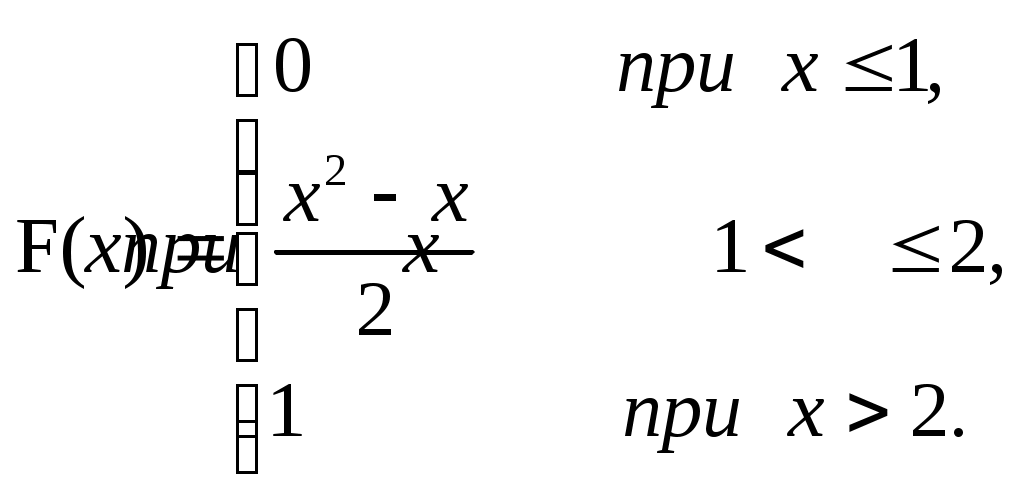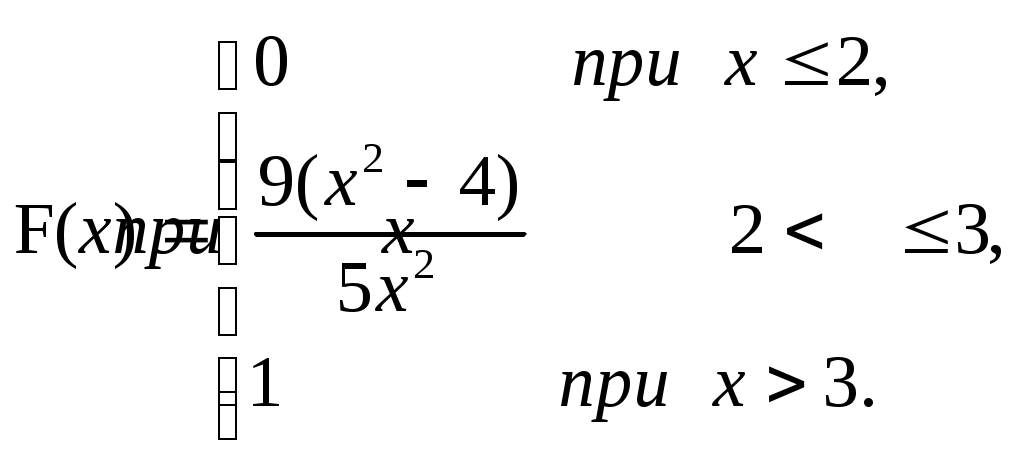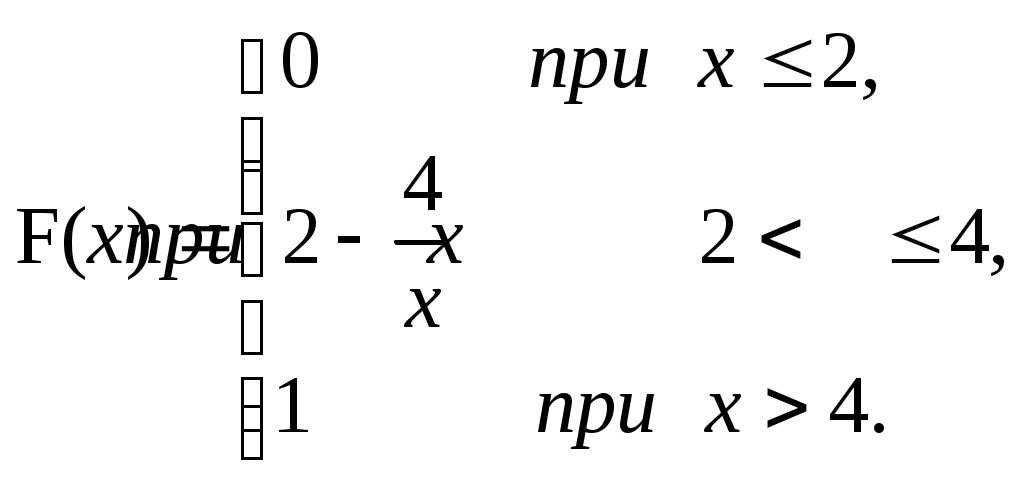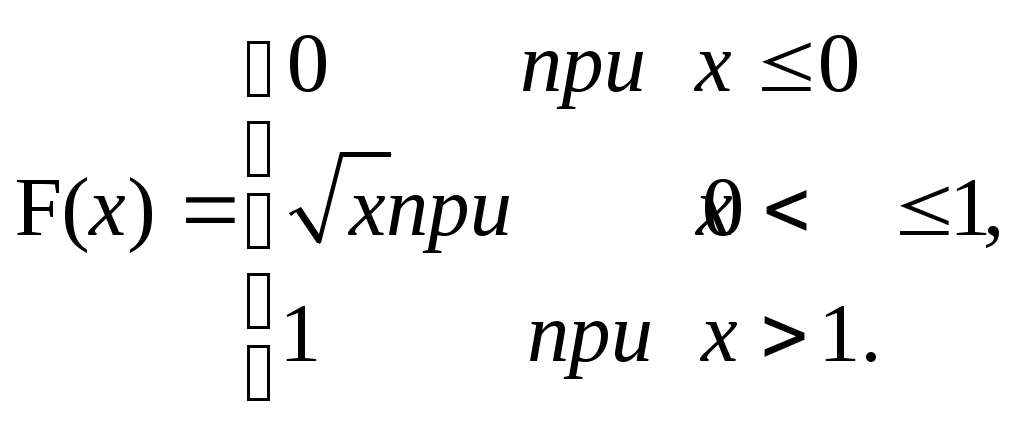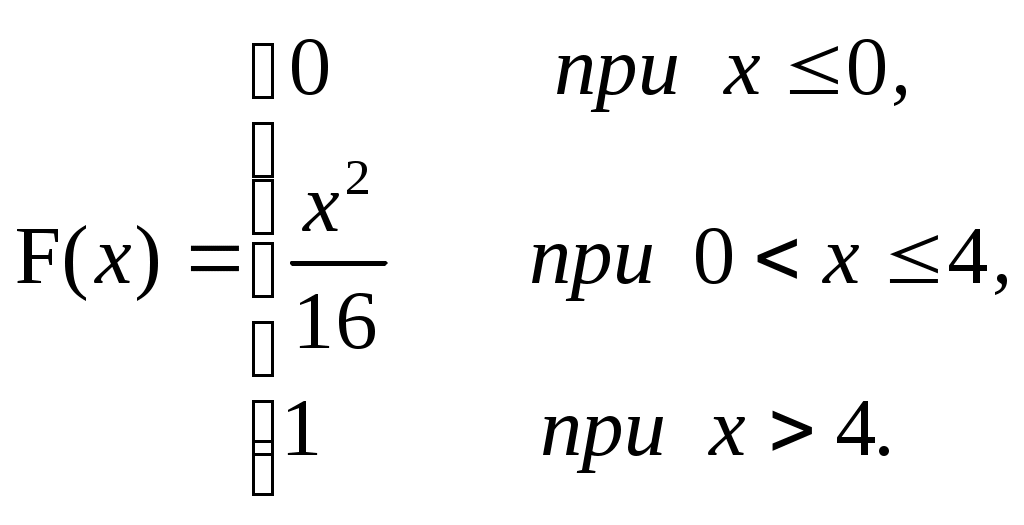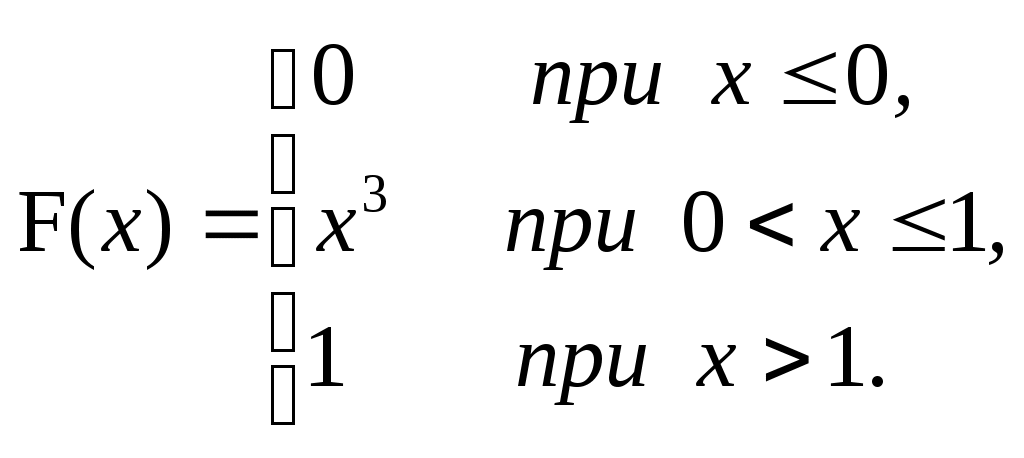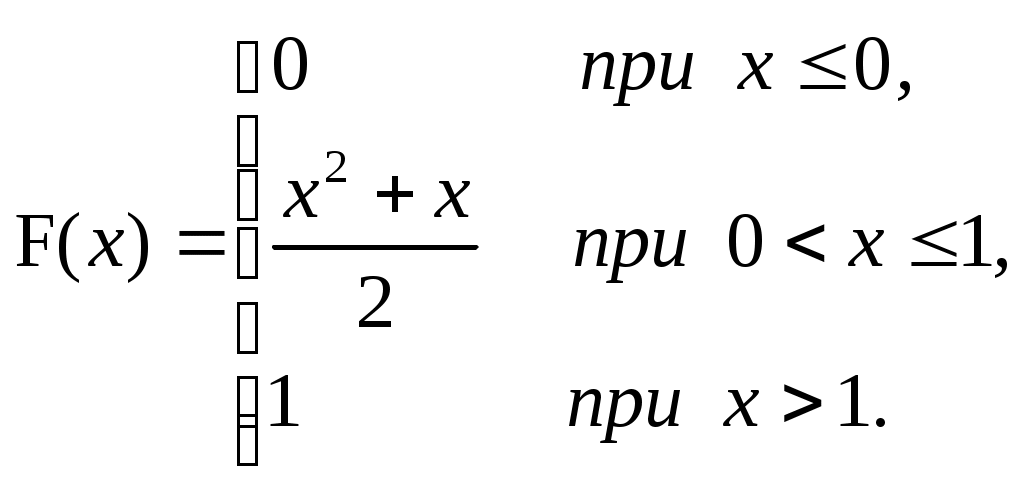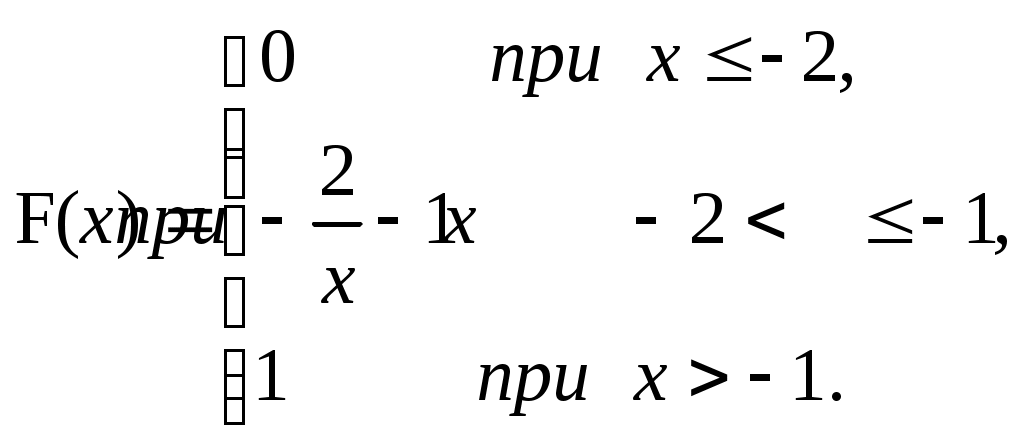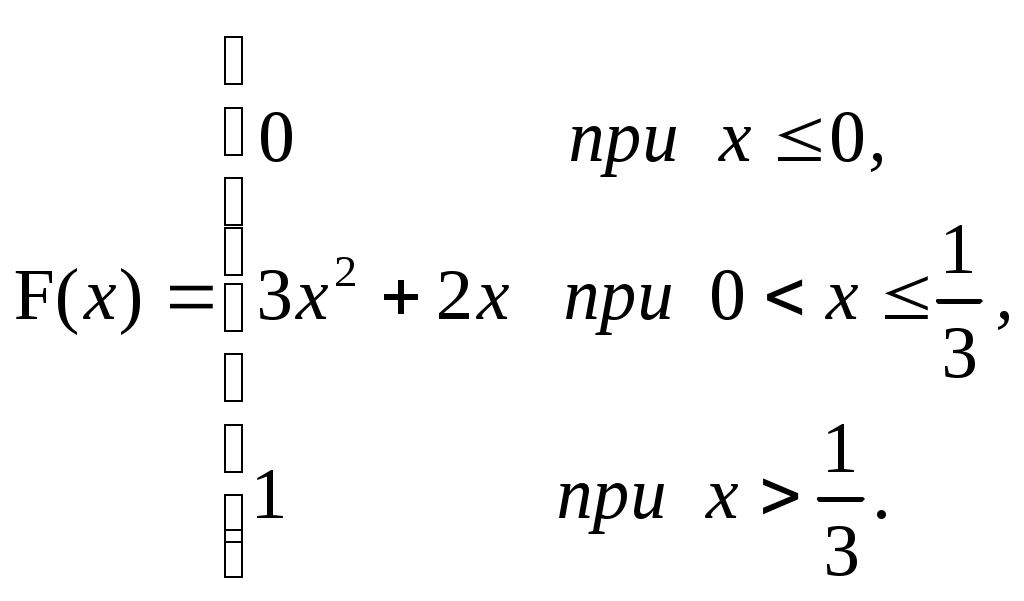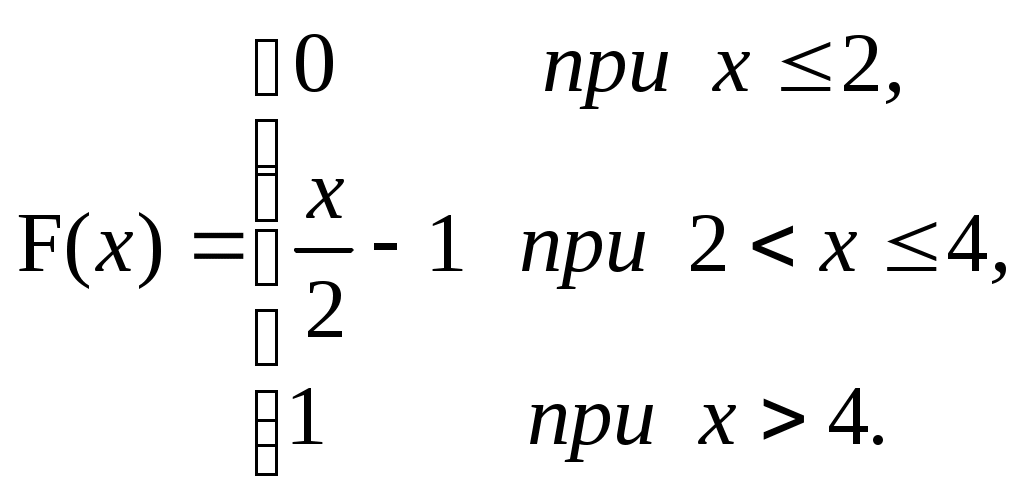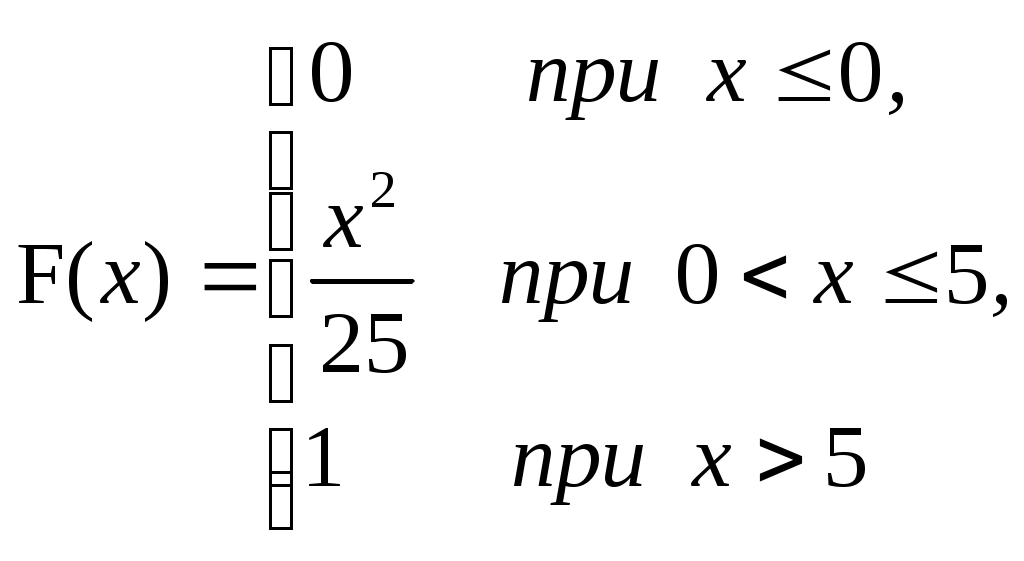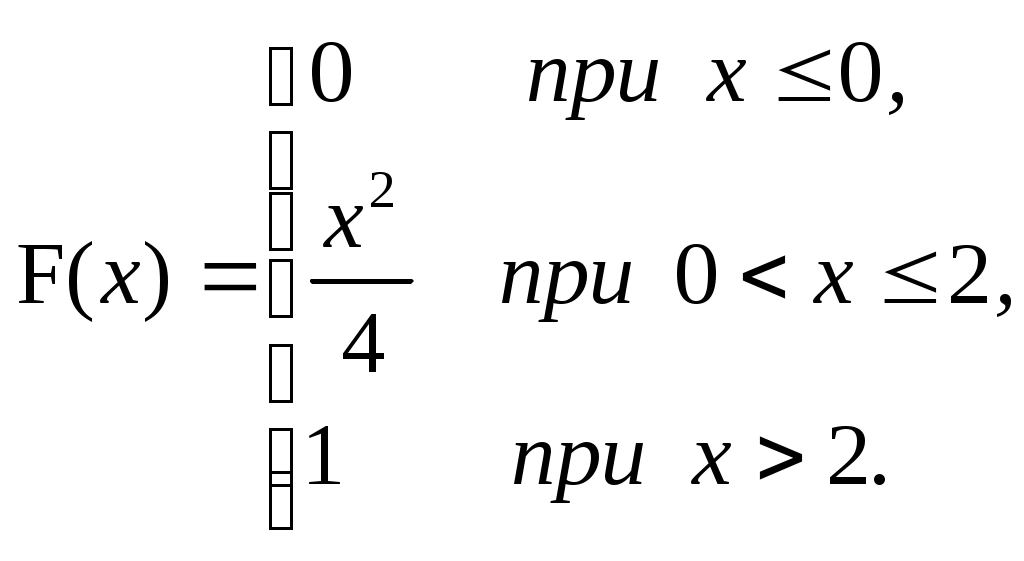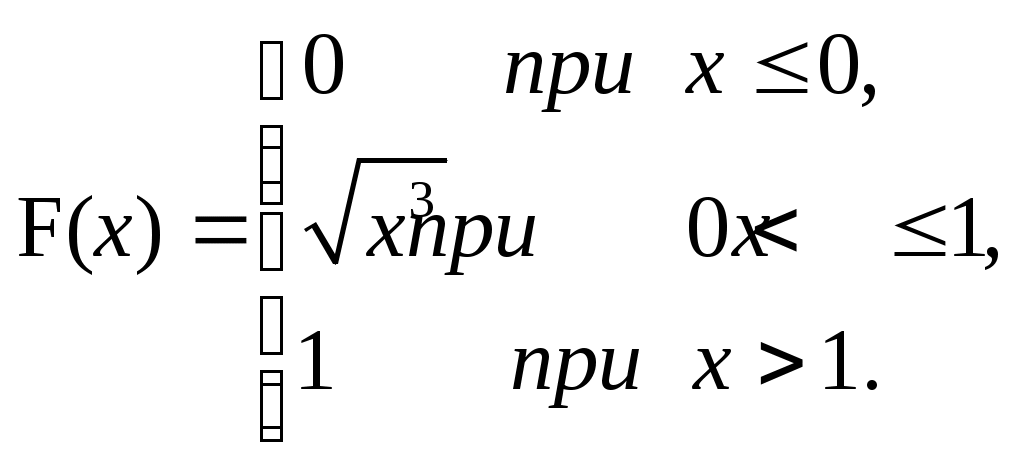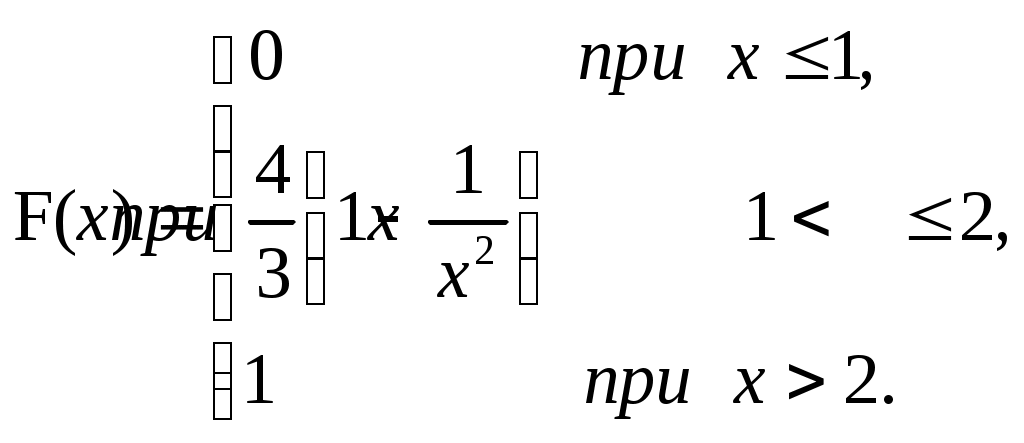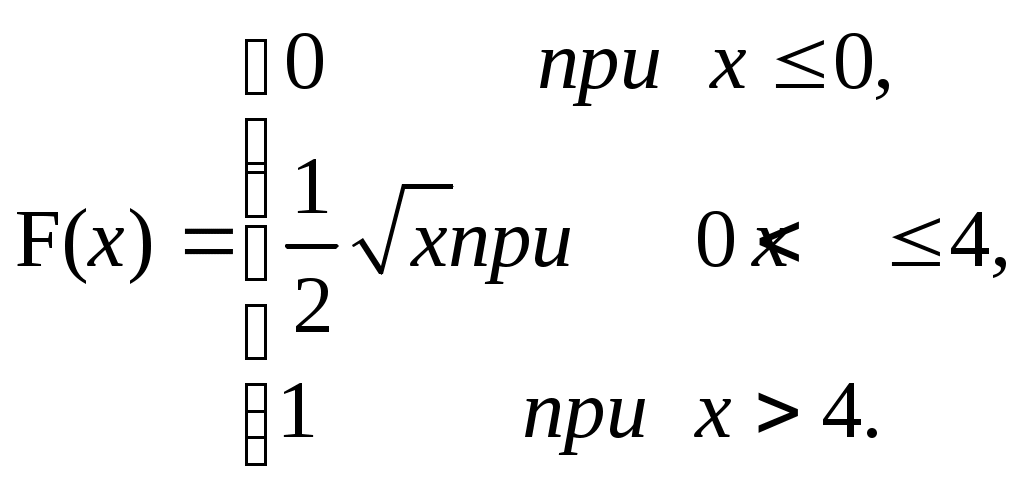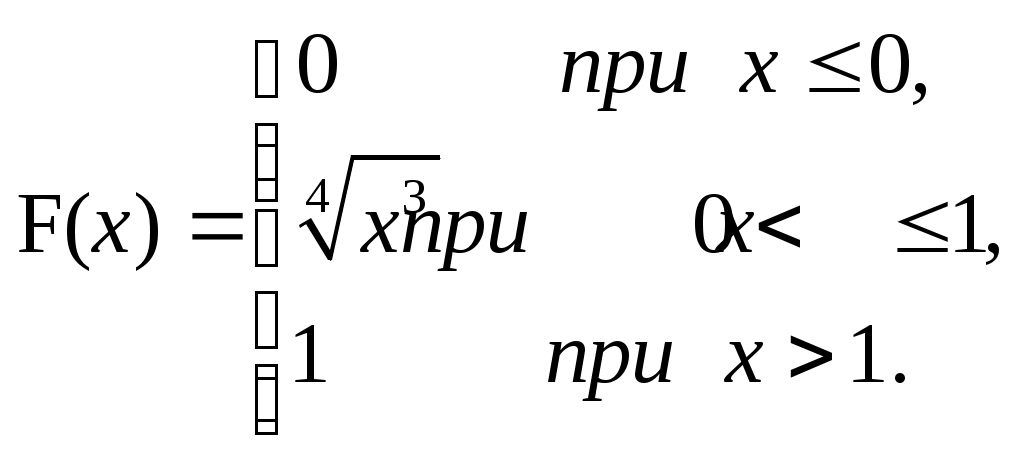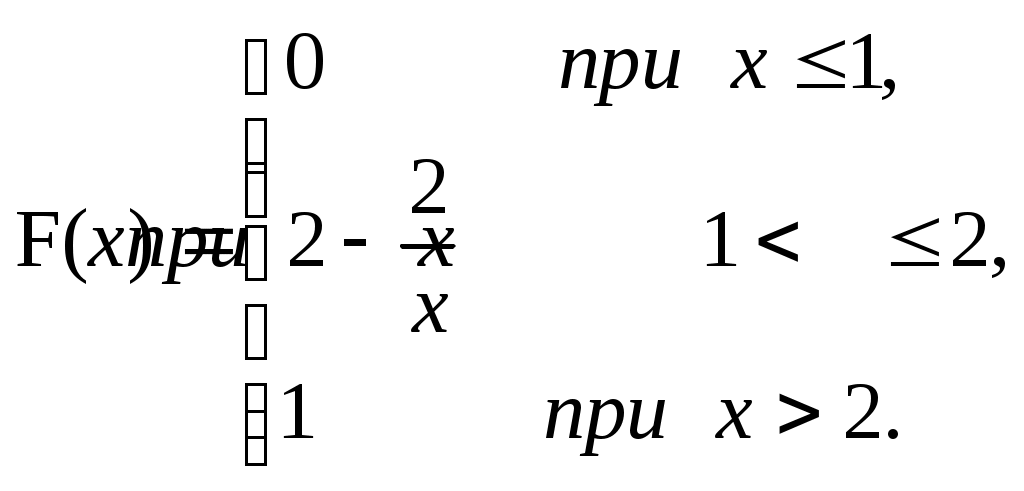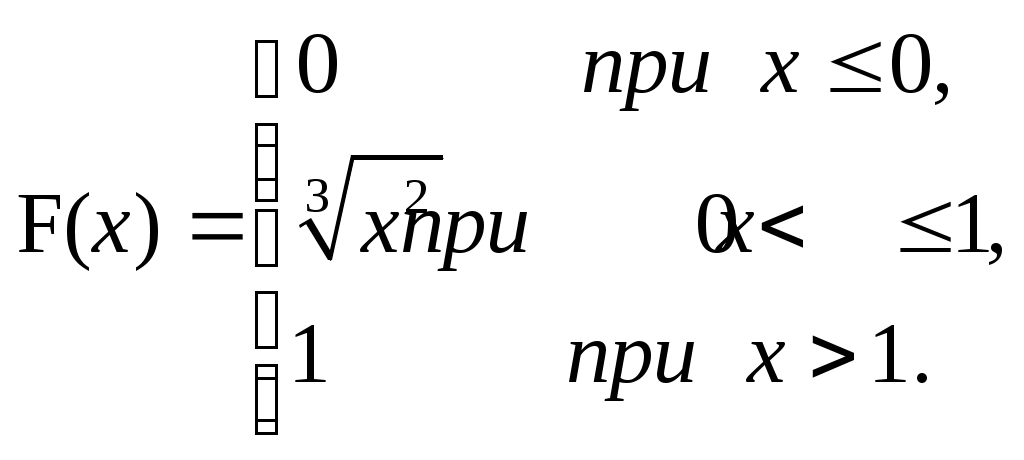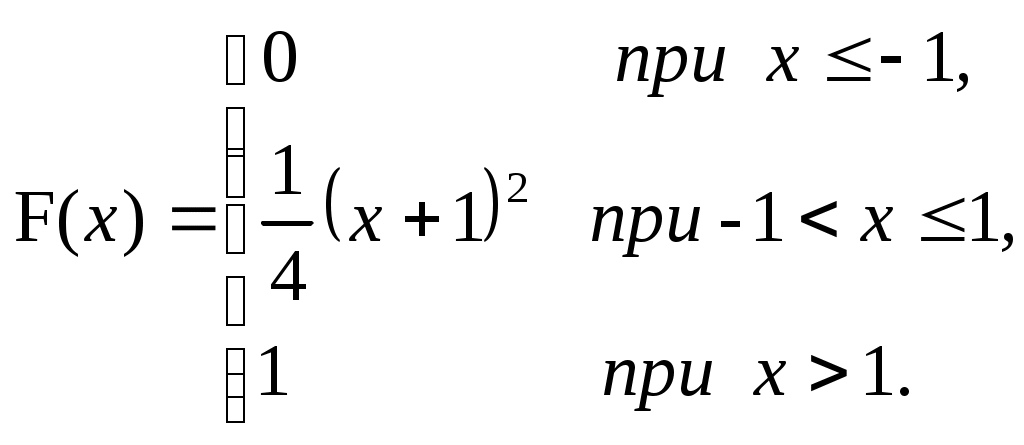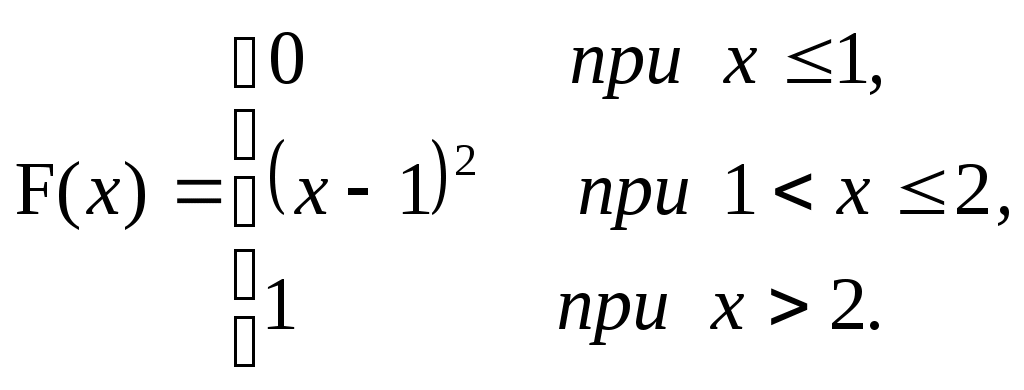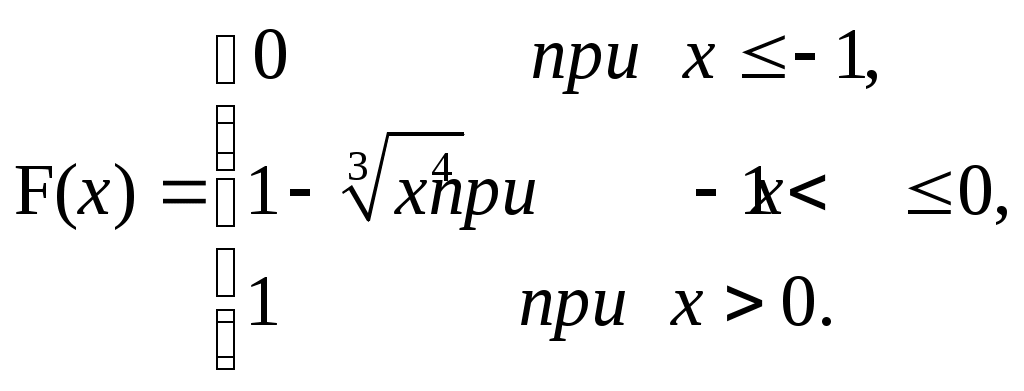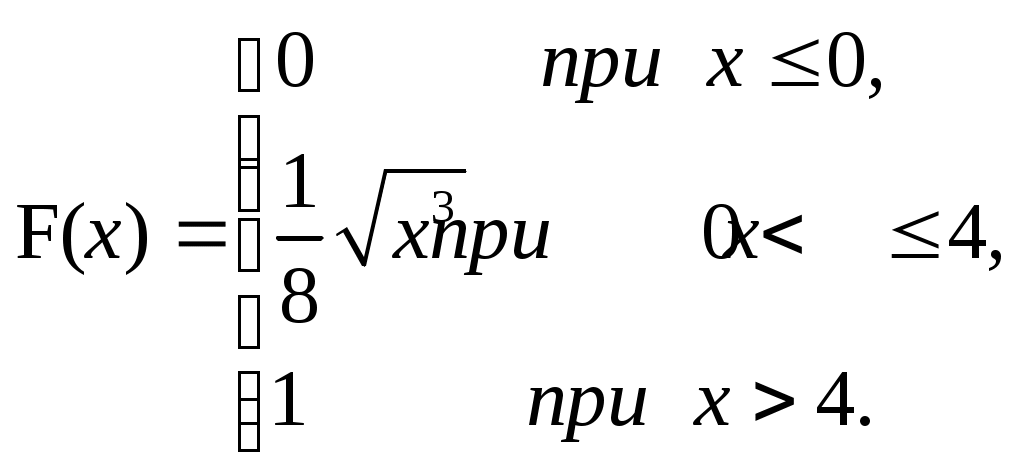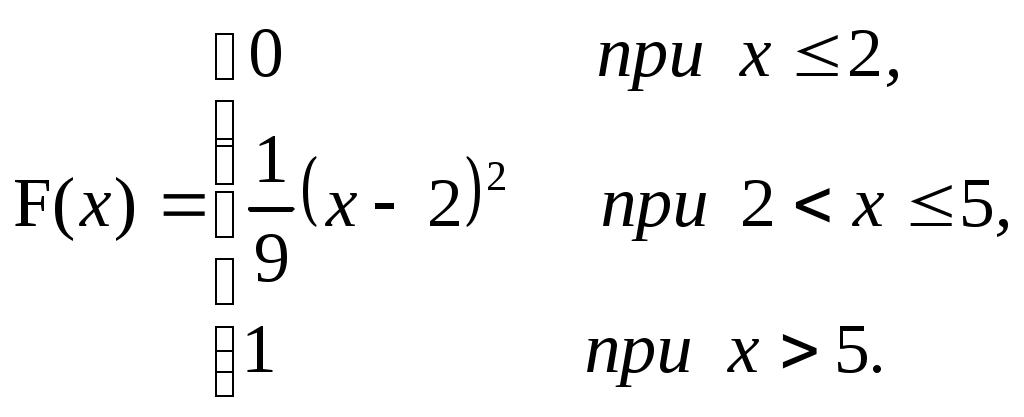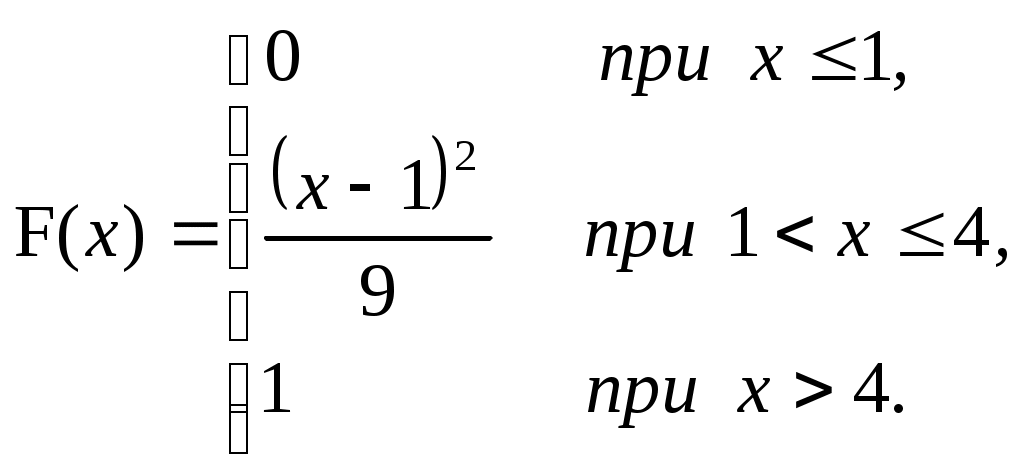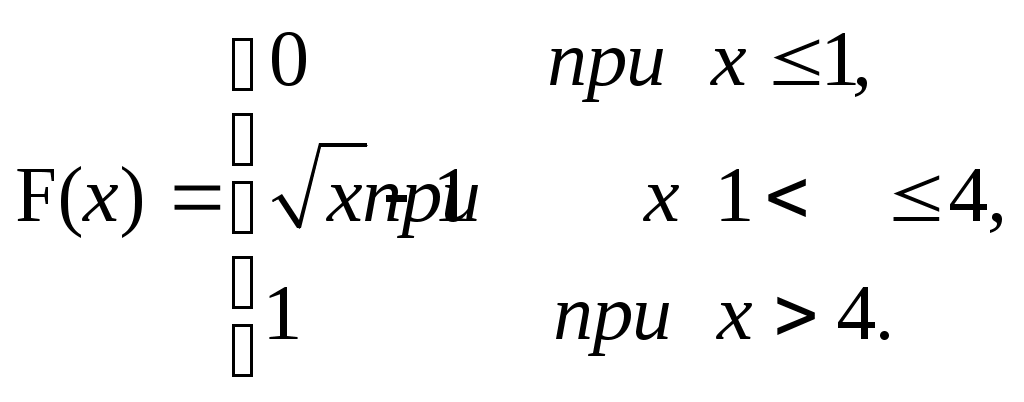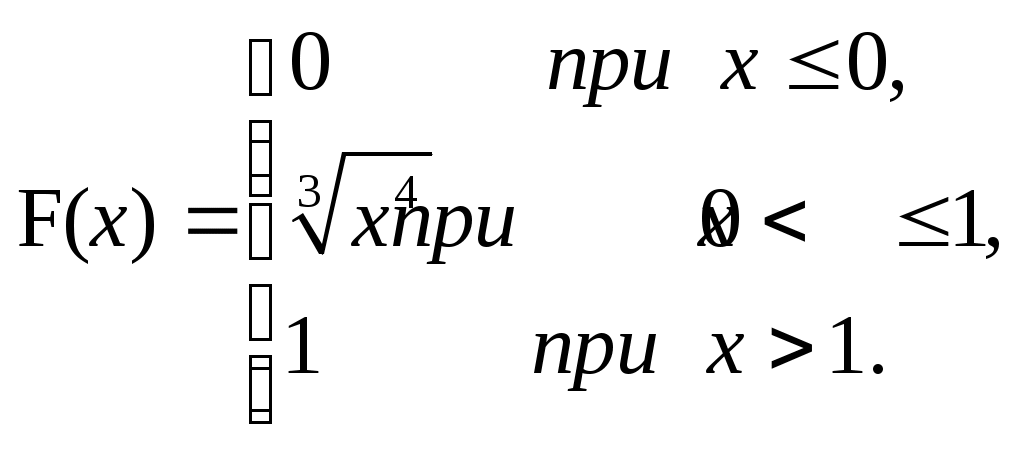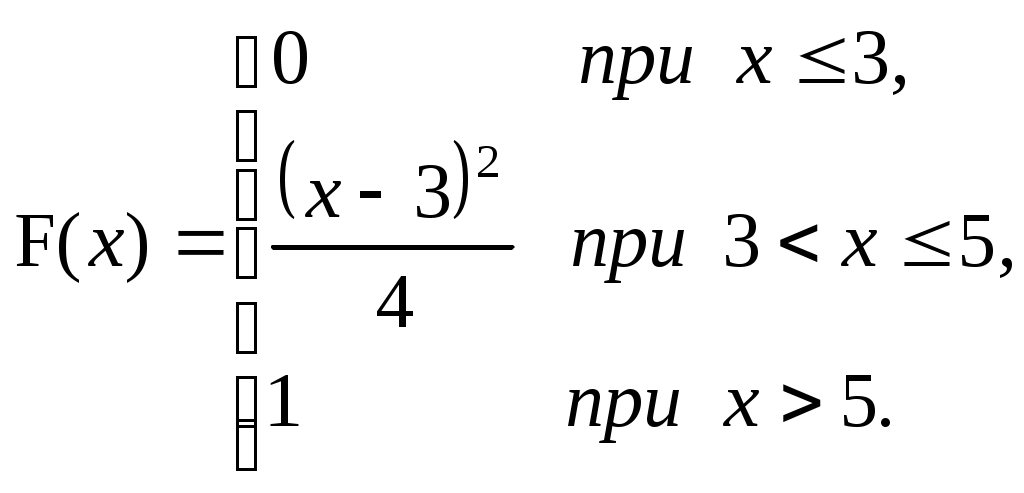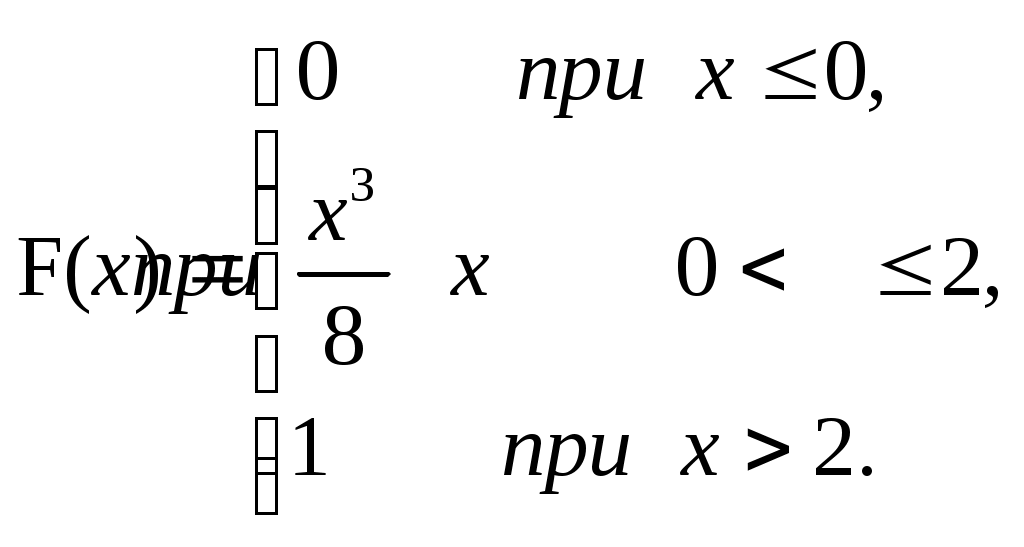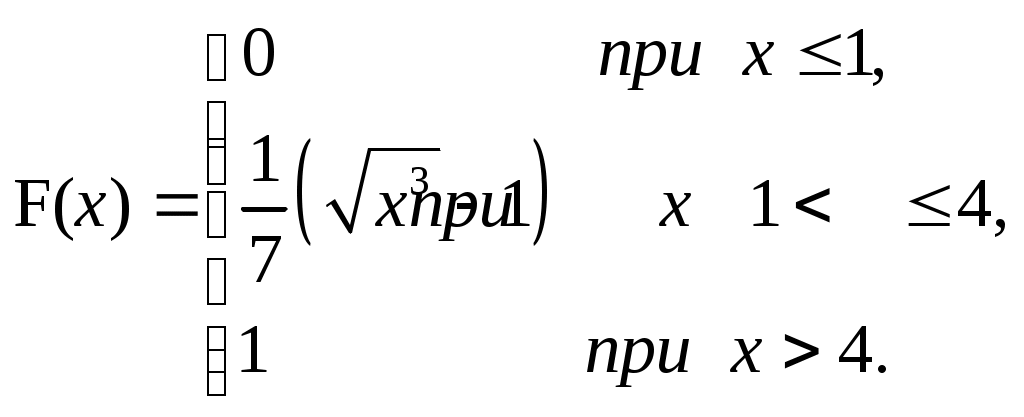Методичні вказівки для самостійної роботи студентів Частина 3 Теорія ймовірностей Математична статистика Житомир 2014
 Скачать 2.83 Mb.
|
ЗАДАЧА 2Теореми додавання та множення ймовірностей2.1 У двох партіях відповідно 75% та 80% доброякісних виробів. Навмання беруть по одному виробу з кожної партії. Знайти ймовірність того, що серед них: а) хоча б один бракований; б) один доброякісний і один бракований. 2.2 При включенні запалення двигун починає працювати з ймовірністю 0,8. Знайти ймовірність того, що для запуску двигуна доведеться включати запалення не більше трьох разів. 2.3 Розрив електричного ланцюга може відбутися внаслідок виходу з ладу одного елемента К1 або одночасного виходу з ладу двох елементів К2 і К3, які виходять з ладу незалежно один від одного з ймовірностями 0,1; 0,2; 0,3 відповідно. Знайти ймовірність розриву ланцюга. 2.4 В механізм входять три однакові деталі. Робота механізму порушиться, якщо при його збиранні будуть встановлені всі три деталі розміру більшого, ніж вказано на кресленні. У складальника 5 деталей із 12 мають більший розмір. Знайти ймовірність нормальної роботи зібраного з цих деталей механізму, якщо складальник бере деталі навмання. 2.5 Ймовірність виготовлення деталі першого ґатунку на першому станку рівна 0,7, на другому – 0,8. На першому станку виготовлено дві деталі, а на другому – три. Знайти ймовірність того, що всі деталі першого ґатунку. 2.6 Робітник обслуговує три верстати. Ймовірність того, що протягом однієї години перший верстат потребує уваги робітника дорівнює 0,3, другий – 0,4 і третій – 0,2. Знайти ймовірність того, що протягом однієї години хоча б один верстат потребує уваги робітника. 2.7 Ймовірність виходу з ладу k-го блоку обчислювальної машини за час t дорівнює k   . Знайти ймовірність того, що за цей час жоден з блоків не вийде з ладу, якщо блоки працюють незалежно.2.8 Ймовірності влучення в мішень для першого, другого та третього спортсмена дорівнюють відповідно 0,9; 0,6; 0,8. Кожен спортсмен робить один постріл. Знайти ймовірність того, що в мішені буде рівно одна пробоїна. 2.9 Серед деталей які виробляє робітник в середньому 4% бракованих. Знайти ймовірність того, що серед взятих п’яти деталей не буде жодної бракованої. 2.10 Деталь проходить три стадії обробки. Ймовірність того, що вона виявиться бракованою на першій стадії обробки, дорівнює 0,02, другій – 0,03, третій – 0,02 .Знайти ймовірність того, що деталь не буде бракованою після трьох стадій, припускаючи, що поява браку на окремих стадіях – незалежні події. 2.11 В цеху 6 двигунів. Кожен двигун працює в даний момент з ймовірністю 0,8. Знайти ймовірність того, що в даний момент працює 4 двигуни. 2.12 З колоди гральних карт (36 штук) навмання дістають чотири карти. Знайти ймовірність того, що серед них буде хоча б один туз. 2.13 Стрілець стріляє по цілі, яка віддаляється. Ймовірність влучення в неї на початку стрільби дорівнює 0,8, а після кожного пострілу зменшується на 0,1. Знайти ймовірність того, що стрілець влучить з третього разу. 2.14 Ймовірність того, що необхідний матеріал є на першій базі дорівнює 0,9, на другій – 0,8, на третій – 0,6. Знайти ймовірність того, що цей матеріал є рівно на двох базах. 2.15 Ймовірність одного влучення в ціль при пострілі з двох гармат дорівнює 0,46. Знайти ймовірність влучення в ціль другою гарматою, якщо для першої гармати ця ймовірність дорівнює 0,7. 2.16 Радист тричі викликає кореспондента. Ймовірність того, що буде прийнято перший виклик дорівнює 0,2, другий – 0,3, третій – 0,4. Події, які полягають в тому, що кореспондент почує виклик, незалежні. Знайти ймовірність того, що кореспондент почує виклик радиста. 2.17 Три верстати працюють незалежно. Ймовірність того, що перший верстат протягом однієї зміни вийде з ладу, дорівнює 0,1, другий – 0,2, третій – 0,3. Знайти ймовірність того, що протягом зміни хоча б один верстат не вийде з ладу. 2.18 Ймовірність того, що протягом однієї зміни виникне несправність верстату, дорівнює 0,05. Знайти ймовірність того, що не виникне жодної несправності за чотири зміни. 2.19 Ймовірність того, що подія D відбудеться хоча б один раз у трьох незалежних випробуваннях, дорівнює 0,784. Знайти ймовірність події D в одному випробуванні, якщо в кожному випробуванні ця ймовірність одна і та сама. 2.20 Для повідомлення про аварію встановлено два незалежно працюючих сигналізатори. Ймовірність того, що при аварії спрацює перший сигналізатор, дорівнює 0,7, другий – 0,9. Знайти ймовірність того, що при аварії: а) спрацюють обидва сигналізатори; б) спрацює хоча б один сигналізатор; в) спрацює рівно один сигналізатор; г) не спрацює жоден сигналізатор. 2.21 Фірму перевіряють незалежно один від одного три аудитори. Ймовірність того, що перший аудитор знайде недоліки становить 0,5; другий – 0,7; третій – 0,4. Знайти ймовірність того, що на фірмі будуть виявлені недоліки. 2.22 Спортсмену надається чотири спроби для виконання кваліфікації. Ймовірність виконання кваліфікації при одній спробі становить 0,8. Знайти ймовірність того, що спортсмен використає всі спроби. 2.23 Є дві коробки, в першій з яких 2 білі та 3 чорні кулі, а в другій – 4 білі та 2 чорні. З кожної коробки виймається по одній кулі. Знайти ймовірність того, що вони одного кольору. 2.24 Партія із 100 виробів проходить вибірковий контроль. Умова непридатності всієї партії – наявність хоча б одного бракованого виробу серед чотирьох, що проходять контроль. Знайти ймовірність того, що ця партія буде забракована, якщо вона містить шість бракованих виробів. 2.25 Ймовірність того, що при одному пострілі стрілець влучить в ціль, дорівнює 0,8. Скільки пострілів повинен зробити стрілець, щоб з ймовірністю не менше 0,99 бути впевненим у влученні в ціль хоча б один раз ? 2.26 В першій коробці 2 білих, 3 червоних і 5 синіх куль, а в другій – 1 біла, 6 червоних і 3 синіх. З кожної коробки дістають навмання по одній кулі. Знайти ймовірність того, що серед цих куль одна синя. 2.27 В магазині продаються 10 телевізорів, три з яких мають дефекти. Яка ймовірність того, що покупцю для придбання телевізора знадобиться не більше двох спроб ? 2.28 На підприємстві брак складає 2% від загальної кількості виробів. Серед небракованих виробів вироби першого ґатунку складають 95%. Знайти ймовірність того, що навмання взятий виріб виявиться першого ґатунку, якщо виріб взято: а) із числа небракованих; б) із загальної маси виготовленої продукції. 2.29 З усіх родин, які мають двох дітей, обрано одну. Усі елементарні події однаково можливі. Знайти ймовірність того, що обидві дитини – хлопчики, якщо відомо, що в сім’ї є хлопчик. 2.30 Студент прийшов на залік знаючи відповіді на 24 питання з 30. Яка ймовірність того, що студент складе залік, якщо після відмови відповісти на запитання викладач буде задавати ще одне питання ? ЗАДАЧА 3 Формула повної ймовірності 3.1 Із 1000 ламп 520 належать першій партії, 90 – другій, а решта третій. В першій партії 8%, в другій – 5%, в третій – 6% бракованих ламп. Яка ймовірність того, що навмання вибрана лампа буде бракованою ? 3.2 В даний район вироби поставляються трьома фірмами у співвідношенні 5:8:7. Серед продукції першої фірми стандартних 90%, другої – 80%, третьої – 75%. Покупцем придбано один виріб. Знайти ймовірність того, що придбаний виріб стандартний. 3.3 В двох коробках знаходиться по 20 деталей, з них стандартних: в першій – 14, в другій – 16. З першої коробки навмання вибрано одну деталь та перекладено в другу. Знайти ймовірність того, що навмання вибрана після цього деталь з другої коробки буде стандартною. 3.4 В тирі є 7 гвинтівок, серед яких три з оптичним прицілом. Ймовірність попадання в ціль при одному пострілі із гвинтівки з оптичним прицілом для даного спортсмена рівна 0,96, без оптичного прицілу – 0,75. Знайти ймовірність попадання в ціль, якщо спортсмен зробить один постріл з навмання вибраної гвинтівки. 3.5 Кількість вантажних авто на даному підприємстві втричі перевищує кількість легкових. Дизельні двигуни мають 50% вантажних авто та 30% легкових. Яка ймовірність того, що навмання вибраний автомобіль матиме дизельний двигун ? 3.6 В двох коробках знаходяться мікросхеми: в першій – 8 мікросхем, з них одна дефектна; в другій – 11, з них дві дефектні. З першої коробки навмання перекладено одну мікросхему в другу коробку. Знайти ймовірність того, що навмання вибрана з другої коробки мікросхема буде дефектною. 3.7 Є мікросхеми двох видів у кількості 18 та 10 штук відповідно. Ймовірність відмови мікросхеми першого виду – 0,03, другого виду – 0,02. Навмання взято одну мікросхему і вмонтовано в електронний вузол. Знайти ймовірність того, що вузол вийде з ладу внаслідок відмови мікросхеми. 3.8 Прилад, встановлений на літаку, може працювати в двох режимах: в умовах нормального польоту та в умовах перевантаження при злеті і посадці. Перший режим здійснюється в 80% всього часу польоту, другий – в 20%. Ймовірність того, що прилад вийде з ладу за час польоту в нормальному режимі рівна 0,2, в умовах перевантаження – 0,4. Знайти ймовірність безвідмовної роботи приладу за час польоту. 3.9 Три автомати виготовляють деталі, які потрапляють на спільний конвеєр. Потужності автоматів відносяться як 2:4:4. Ймовірність того, що якість деталі відмінна для цих автоматів відповідно рівна: 0,7; 0,8 і 0,9. Знайти ймовірність того, що навмання взята з конвеєра деталь буде відмінної якості. 3.10 В тирі є п’ять рушниць, ймовірність влучення в мішень з яких при одному пострілі рівна відповідно 0,5; 0,8; 0,7; 0,6; 0,9. Визначити ймовірність попадання в мішень при одному пострілі, якщо рушниця вибирається навмання. 3.11 В першій коробці знаходиться 8 білих та 3 чорних кульки, в другій – 4 білих та 6 чорних. З першої коробки в другу переклали навмання 2 кульки. Після чого, з другої коробки виймають одну кульку. Знайти ймовірність того, що вона біла. 3.12 В артилерійській військовій частині 20 гармат, з них чотири непристріляні. Ймовірність попадання в ціль з пристріляної гармати рівна 0,8, з непристріляної – 0,3. Знайти ймовірність враження цілі, якщо буде зроблено один постріл з навмання вибраної гармати. 3.13 На заводі по виготовленню болтів перший станок виробляє 25%, другий – 35%, третій – 40% всіх виробів. В їх продукції брак складає відповідно 3%, 2% та 1%. Знайти ймовірність того, що навмання вибраний болт не є бракованим. 3.14 Радіолампа може належати до однієї з чотирьох партій з ймовірностями р1=0,2, р2=0,4, р3=0,3, р4=0,1. Ймовірність того, що лампа пропрацює заданий час, для цих партій рівна відповідно 0,5; 0,7; 0,6; 0,8. Знайти ймовірність того, що навмання вибрана лампа пропрацює заданий час. 3.15 Стріляють по 9 мішенях типу X, по шести – типу Y і по п’яти – типу Z. Ймовірність попадання при одному пострілі в мішень типу X рівна 0,6, типу Y – 0,5, типу Z – 0,8. Знайти ймовірність враження мішені при одному пострілі, якщо мішень вибирається навмання. 3.16 З першого автомата на конвеєр потрапляє 30%, з другого – 25%, з третього – 20%, з четвертого – 25% деталей. Серед деталей першого автомата 1% бракованих, другого – 2%, третього – 1%, з четвертого – 5%. Знайти ймовірність того, що навмання вибрана з конвеєра деталь виявиться бракованою. 3.17 В коробці знаходиться 25 деталей, виготовлених на першому заводі, 14 – на другому, 20 – на третьому. Серед деталей, виготовлених на першому заводі, 80% відмінної якості, на другому – 70%, на третьому – 90%. Знайти ймовірність того, що навмання вибрана з коробки деталь виявиться відмінної якості. 3.18 Є дві партії виробів по 20 шт. кожна, при чому в кожній з них є по два бракованих вироби. Виріб, навмання вибраний з першої партії, перекладено в другу, після чого навмання вибрано виріб з другої партії. Знайти ймовірність того, що цей виріб виявиться бракованим. 3.19 На деякому підприємстві перша машина виробляє 15%, друга – 45%, третя – 40% всіх деталей. В їх продукції браку, відповідно 8, 6, 3%. Яка ймовірність того, що навмання вибрана деталь небракована ? 3.20 Деталі виготовляють на двох заводах. Об’єм продукції другого заводу в два рази більший, ніж першого. Серед деталей першого заводу 5% бракованих, другого – 3%. Знайти ймовірність того, що навмання вибрана деталь виявиться небракованою. 3.21 Працівник друкарні, при наборі тексту, користується двома комплектами літер: в першому – 80%, в другому – 95% шрифту відмінної якості. Знайти ймовірність того, що навмання вибрана літера з навмання вибраного комплекту виявиться відмінної якості. 3.22 Виріб перевіряється на стандартність одним з двох контролерів. Ймовірність того, що виріб потрапить до першого контролера рівна 0,6, до другого – 0,4. Ймовірність того, що стандартний виріб буде визнано стандартним першим контролером, рівна 0,92, другим – 0,99. Знайти ймовірність того, що стандартний виріб при перевірці буде визнано стандартним. 3.23 В продаж надходять телевізори трьох заводів. Продукція першого заводу містить 10% телевізорів з прихованим дефектом, другого – 4%, третього – 6%. Знайти ймовірність придбання справного телевізора, якщо магазин одержав 20% телевізорів з першого заводу, 45% – з другого, 35 – з третього. 3.24 Ймовірності того, що під час роботи комп’ютера збій виникне в процесорі, в оперативній пам’яті, в інших вузлах відносяться як 2:3:5. Ймовірності виявлення збою в процесорі, в оперативній пам’яті та в інших вузлах відповідно рівні 0,85; 0,95; 0,8. Знайти ймовірність того, що збій, який виник в машині, буде виявлено. 3.25 В цеху працює 26 верстатів. З них 12 марки X, 8 марки Y і 6 марки Z. Верстати виготовляють відповідно 80%, 70% і 90% деталей відмінної якості. Який процент деталей відмінної якості випускає цех в цілому, якщо продуктивність верстатів однакова ? 3.26 Торгова фірма одержує телевізори від трьох виробників у співвідношенні 1:4:5. Досвід показує, що телевізори цих виробників не потребують ремонту на протязі гарантійного терміну відповідно в 98%, 88% та 92% випадків. Знайти ймовірність того, що придбаний покупцем телевізор не потребуватиме ремонту на протязі гарантійного терміну. 3.27 В першій коробці знаходиться 3 білих та 7 чорних кульок, в другій – 4 білі та 6 чорних, в третій – 8 білих та 2 чорних. Знайти ймовірність того, що навмання вибрана кулька з навмання вибраної коробки виявиться чорною. 3.28 В коробку з трьома однаковими деталями кинуто стандартну деталь, а потім навмання вибрано одну деталь. Знайти ймовірність того, що вона стандартна, якщо однаково ймовірні всі гіпотези про початкову кількість стандартних деталей в коробці. 3.29 В кошику знаходиться 10 тенісних м’ячів, 8 з яких нові. Для першої гри беруть навмання один м’яч, який після гри повертають в кошик. Для другої гри також навмання беруть м’яч. Знайти ймовірність того, що взятий для другої гри м’яч новий. 3.30 В першій коробці знаходиться 10 куль, з яких 8 білих; в другій – 20 куль, з яких 4 білі. З кожного ящика навмання дістають по одній кулі, а потім з цих двох куль навмання вибирають одну кулю. Знайти ймовірність того, що це буде біла куля. ЗАДАЧА 4Формула Байєса 4.1 В даний район вироби постачаються трьома фірмами у співвідношенні 5:4:6. Серед продукції першої фірми стандартних 80%, другої – 90%, третьої – 85%. Покупцем придбано один виріб, який виявився стандартним. Знайти ймовірність того, що він поставлений першою фірмою. 4.2 Серед 25 гранітних блоків 5 – червоного граніту, решта – сірого. Відомо, що 10% блоків червоного та 15% сірого мають внутрішні дефекти. Навмання вибраний для дослідження блок виявився дефектним. Яка ймовірність того, що він з сірого граніту? 4.3 В тирі є 5 гвинтівок, серед яких лише дві з оптичним прицілом. Ймовірність попадання в ціль при одному пострілі із гвинтівки з оптичним прицілом для даного спортсмена рівна 0,95, без оптичного прицілу – 0,70. Спортсмен одним пострілом з навмання вибраної гвинтівки вразив ціль. Знайти ймовірність того, що він стріляв з гвинтівки без оптичного прицілу. 4.4 На деякому підприємстві перша машина виробляє 15%, друга – 45%, третя – 40% всіх деталей. В їх продукції браку, відповідно 8, 6, 3%. Випадково вибрана деталь виявилась дефектною. Яка ймовірність того, що вона виготовлена другою машиною? 4.5 В продаж надходять телевізори трьох заводів. Продукція першого заводу містить 6% телевізорів з прихованим дефектом, другого – 5%, третього – 4%. Магазин одержав 20% телевізорів з першого заводу, 45% – з другого, 35% – з третього. Придбаний телевізор виявився справним. Знайти ймовірність того, що його виготовлено на першому заводі. 4.6 Виріб перевіряється на стандартність одним з двох контролерів. Ймовірність того, що виріб потрапить до першого контролера рівна 0,55, до другого – 0,45. Ймовірність того, що стандартний виріб буде визнано стандартним першим контролером, рівна 0,9, другим – 0,98. Стандартний виріб при перевірці визнано стандартним. Знайти ймовірність того, що перевірка здійснювалась другим контролером. 4.7 З першого автомата на конвеєр потрапляє 40%, з другого – 20%, з третього – 10%, з четвертого – 30% деталей. Серед деталей першого автомата 2% бракованих, другого – 3%, третього – 4%, з четвертого – 1%. Знайти ймовірність того, що навмання вибрана з конвеєра деталь, яка виявилась бракованою, виготовлена третім автоматом. 4.8 В першій коробці знаходиться 7 білих та 5 чорних кульок, в другій – 1 біла та 6 чорних. З першої коробки в другу переклали навмання одну кульку. Після чого, з другої коробки навмання виймають одну кульку, яка виявилась чорною. Знайти ймовірність того, що було перекладено білу кульку. 4.9 Працівник друкарні, при наборі тексту, користується двома комплектами літер: в першому – 85%, в другому – 90% шрифту відмінної якості. Знайти ймовірність того, що навмання вибрана літера, яка виявилась відмінної якості, належить до першого комплекту. 4.10 Кількість вантажних авто на даному підприємстві вдвічі перевищує кількість легкових. Дизельні двигуни мають 50% вантажних авто та 10% легкових. Яка ймовірність того, що навмання вибраний автомобіль, який виявився з дизельним двигуном, є вантажним? 4.11 Серед 16 одиниць продукції першого виду 15% браку, а серед 30 одиниць другого виду 6% браку. Навмання вибрана одиниця продукції виявилась бракованою. Яка ймовірність того, що вона другого виду? 4.12 На деякому підприємстві перша машина виробляє 25%, друга – 35%, третя – 40% всіх деталей. В їх продукції браку відповідно 6, 5 та 4%. Яка ймовірність того, що випадково вибрана деталь, яка виявилась дефектною, виготовлена першою машиною? 4.13 Є 32 одиниці продукції двох видів. Серед 12 одиниць продукції першого виду 5% браку, а серед 20 одиниць другого виду 10% браку. Навмання вибрана одиниця продукції виявилась бракованою. Яка ймовірність того, що вона другого виду? 4.14 В двох коробках знаходиться по 20 деталей, з них стандартних: в першій – 18, в другій – 10. З першої коробки навмання вибрано одну деталь та перекладено в другу. Навмання вибрана після цього деталь з другої коробки виявилась стандартною. Знайти ймовірність того, що було перекладено нестандартну деталь. 4.15 В коробці знаходиться 16 деталей, виготовлених на першому заводі, 14 – на другому, 10 – на третьому Серед деталей, виготовлених на першому заводі, 90% відмінної якості, на другому – 80%, на третьому – 70%. Навмання вибрана з коробки деталь виявилась відмінної якості. Знайти ймовірність того, що її виготовлено на третьому заводі. 4.16 Стріляють по двох мішенях типу X, по шести – типу Y і по п’яти – типу Z. Ймовірність попадання при одному пострілі в мішень типу X рівна 0,6, типу Y – 0,5, типу Z – 0,4. При одному пострілі мішень було вражено. Знайти ймовірність того, що стріляли по мішені типу Y, якщо мішень вибирається навмання. 4.17 Прилад, встановлений на літаку, може працювати в двох режимах: в умовах нормального польоту та в умовах перевантаження при злеті і посадці. Перший режим здійснюється в 80% всього часу польоту, другий – в 20%. Ймовірність того, що прилад вийде з ладу за час польоту в нормальному режимі рівна 0,2, в умовах перевантаження – 0,4. Прилад вийшов з ладу за час польоту. Знайти ймовірність того, що це сталось в умовах перевантаження при злеті і посадці. 4.18 Деталі виготовляють на двох заводах. Об’єм продукції другого заводу в три рази більший, ніж першого. Серед деталей першого заводу 8% бракованих, другого – 2%. Знайти ймовірність того, що навмання вибрана деталь, яка виявилась бракованою, виготовлена на першому заводі. 4.19 Ймовірності того, що під час роботи комп’ютера збій виникне в процесорі, в оперативній пам’яті, в інших вузлах відносяться як 3:4:3. Ймовірності виявлення збою в процесорі, в оперативній пам’яті та в інших вузлах відповідно рівні 0,85; 0,95; 0,8. Знайти ймовірність того, що збій, який виявлено в машині, виник в процесорі. 4.20 На заводі по виготовленню болтів перший станок виробляє 15%, другий – 25%, третій – 60% всіх виробів. В їх продукції брак складає відповідно 2%, 1% та 3%. Знайти ймовірність того, що випадково вибраний болт, який виявився дефектним, виготовлено на третьому станку. 4.21 Відомо, що 90% продукції заводу відповідає стандарту. Спрощена схема контролю визнає придатною стандартну продукцію з ймовірністю 0,98 та нестандартну – з ймовірністю 0,05. Знайти ймовірність того, що виріб, який пройшов спрощений контроль, задовольняє стандарту. 4.22 В першій коробці знаходиться 5 білих та 8 чорних кульок, в другій – 2 білі та 7 чорних, в третій – 5 білих та 3 чорних. З навмання вибраної коробки вийнято кульку. Вона виявилась білою. Знайти ймовірність того, що кульку вийнято з другої коробки. 4.23 Однотипні прилади випускаються трьома заводами в кількісному співвідношенні 5:2:3, причому ймовірність браку для цих заводів відповідно рівна 0,04; 0,1; 0,05. Прилад, придбаний лабораторією, виявився бракованим. Знайти ймовірність того, що даний прилад виготовлено другим заводом. 4.24 Маємо 10 однакових коробок, в семи з яких міститься по чотири чорних та три білих, а в трьох – по сім чорних та п’ять білих кульок. З навмання вибраної коробки вийнято кульку. Вона виявилась білою. Знайти ймовірність того, що кульку вийнято з коробки, в якій знаходиться чотири чорних та три білих кульки. 4.25 Серед 300 виробів 150 першого ґатунку, 100 – другого, 50 – третього. Ймовірність браку серед виробів першого ґатунку 0,02, другого – 0,03, третього – 0,05. Взятий навмання виріб, виявився небракованим. Знайти ймовірність того, що цей виріб першого ґатунку. 4.26 В артилерійській військовій частині 18 гармат, з них дві непристріляні. Ймовірність попадання в ціль з пристріляної гармати рівна 0,8, з непристріляної – 0,3. Зробили один постріл і ціль не вразили. Знайти ймовірність того, що постріл зроблено з непристріляної гармати. 4.27 Радіолампа може належати до однієї з трьох партій з ймовірностями р1=0,2, р2=0,5, р3=0,3. Ймовірність того, що лампа пропрацює заданий час, для цих партій рівна відповідно 0,5; 0,4; 0,8. Лампа пропрацювала заданий час. Знайти ймовірність того, що вона належить першій партії. 4.28 В тирі є чотири рушниці, ймовірності влучення з яких в мішень при одному пострілі рівні відповідно 0,8; 0,9; 0,7; 0,5. При одному пострілі було влучено в мішень. Знайти ймовірність того, що постріл було зроблено з другої рушниці, якщо рушниця вибирається навмання. 4.29 В коробці лежить куля невідомого кольору – з однаковою ймовірністю біла або чорна. В коробку поклали одну білу кулю і після старанного перемішування навмання дістали одну кулю. Вона виявилась білою. Знайти ймовірність того, що в коробці залишилась біла куля. 4.30 Два мисливці одночасно вистрілили по кабану. Ймовірності влучення для мисливців відповідно дорівнюють 0,8 і 0,4. Кабана вбито однією кулею. В якому співвідношенні мисливці повинні розділити здобич ? ЗАДАЧА 5Дискретна випадкова величина 5.1–5.6 Маємо n ламп, кожна з яких з ймовірністю р є якісною. Лампа вгвинчується в прилад і вмикається струм. При вмиканні струму дефектна лампа одразу виходить з ладу, після чого замінюється іншою. Розглядається випадкова величина Х – число випробуваних ламп. Побудувати її закон розподілу та знайти математичне сподівання, дисперсію і середнє квадратичне відхилення.
5.7–5.12 Випробовується пристрій, який складається з трьох незалежно працюючих приладів. Ймовірності відмови приладів р1, р2, р3 . Розглядається випадкова величина Х – число приладів, які вийшли з ладу. Побудувати її закон розподілу та знайти математичне сподівання, дисперсію і середнє квадратичне відхилення.
5.13–5.18 Два спортсмени незалежно роблять по одному пострілу, кожен в свою мішень. Ймовірність влучення в мішень для першого спортсмена – р1, для другого – р2. Розглядаються випадкові величини:  – число влучень першого спортсмена,  – число влучень другого спортсмена та їх різниця  . Побудувати закон розподілу випадкової величини Z та знайти її математичне сподівання, дисперсію і середнє квадратичне відхилення.
5.19–5.24 В коробці k білих та n чорних кульок. Дві кульки навмання дістають з коробки. Розглядається випадкова величина Х – число вийнятих білих кульок. Побудувати її закон розподілу та знайти математичне сподівання, дисперсію і середнє квадратичне відхилення.
5.25–5.27 Правильний гральний кубик підкидається n разів. Розглядається випадкова величина Х – випаде не менше п’яти очок. Побудувати її закон розподілу та знайти математичне сподівання, дисперсію і середнє квадратичне відхилення.
5.28–5.30 Симетрична монета підкидається n разів. Розглядається випадкова величина Х – число появ герба. Побудувати її закон розподілу та знайти математичне сподівання, дисперсію і середнє квадратичне відхилення.
ЗАДАЧА 6Неперервна випадкова величина Випадкова величина Х має функцію розподілу  . Знайти: ймовірність попадання в інтервал (; ), щільність розподілу, математичне сподівання, дисперсію та середнє квадратичне відхилення. Побудувати графіки функції розподілу та щільності розподілу.
МАТЕМАТИЧНА СТАТИСТИКА |
