Математична статистика
Приклад 1. Дано вибірку: 1, 3, 4, 5, 1, 3, 4, 3, 5, 1, 3, 4, 1, 3, 4, 3, 4, 3, 4, 3.
Потрібно:
побудувати варіаційний ряд;
побудувати статистичний розподіл вибірки;
побудувати полігон відносних частот;
знайти емпіричну функцію розподілу і побудувати її графік.
Розв’язання.
1) Побудуємо варіаційний ряд
1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5.
2) Порахуємо частоти з якими варіанти xi входять у вибірку та запишемо статистичний розподіл вибірки:
3) Знайдемо відносні частоти. Оскільки об’єм вибірки n =4+8+6+2=20, то w1 =4/20=0,2; w2 =8/20=0,4; w3 =6/20=0,3; w4 =2/20=0,1.
Отже розподіл відносних частот має вигляд:
xі
|
1
|
3
|
4
|
5
|
wі
|
0,2
|
0,4
|
0,3
|
0,1
|
На площині (хі; wі) зобразимо точки з координатами (1;0,2), (3;0,4), (4;0,3), (5;0,1) та з’єднаємо їх відрізками. Отримаємо шуканий полігон відносних частот.
4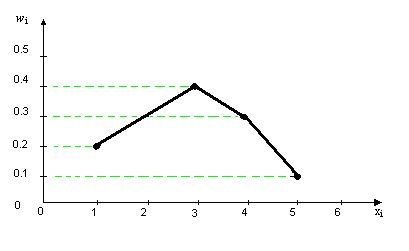
) Емпіричну функцію розподілу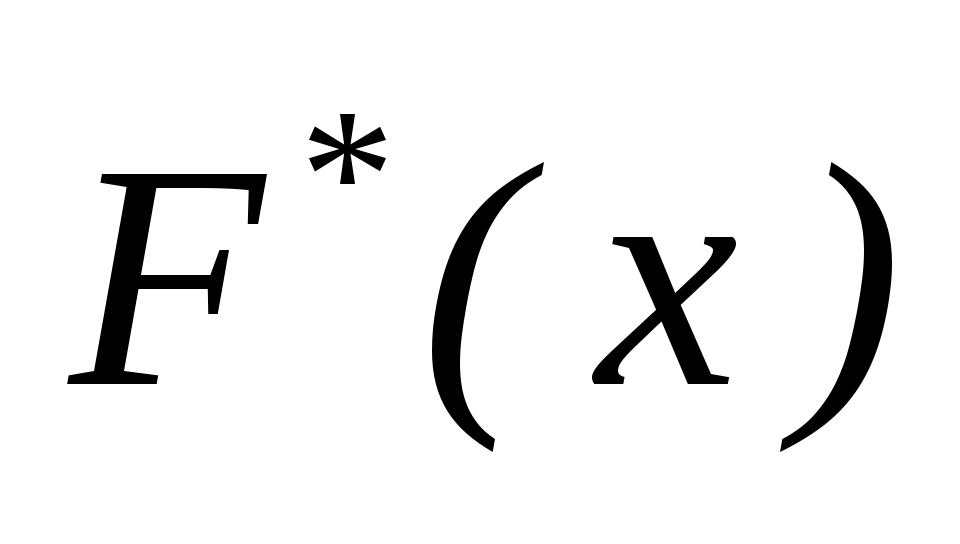 знаходимо за формулою: знаходимо за формулою:
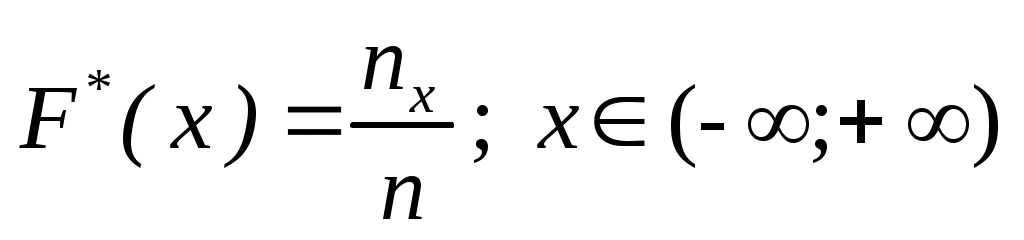 , де , де 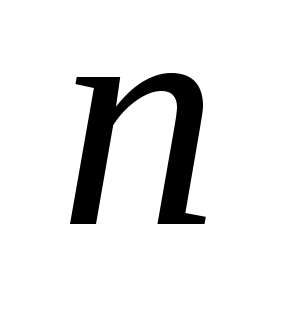 – об’єм вибірки ; – об’єм вибірки ; 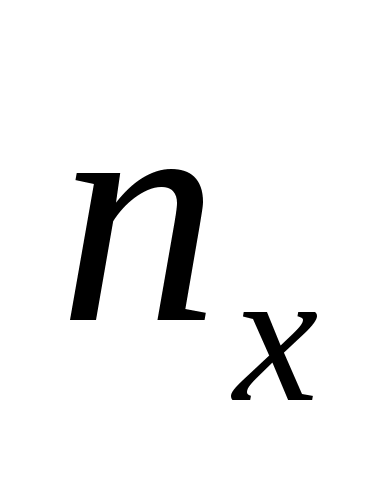 - число варіант, які менші - число варіант, які менші 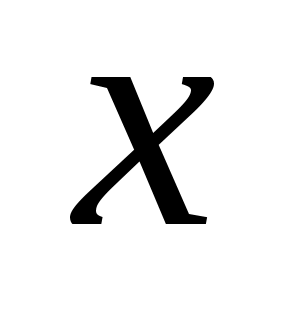 . В даній задачі . В даній задачі 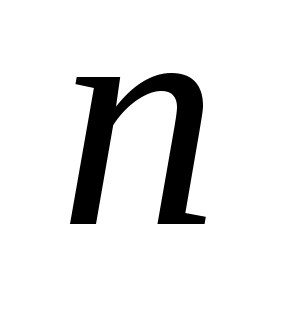 = 20. = 20.
При 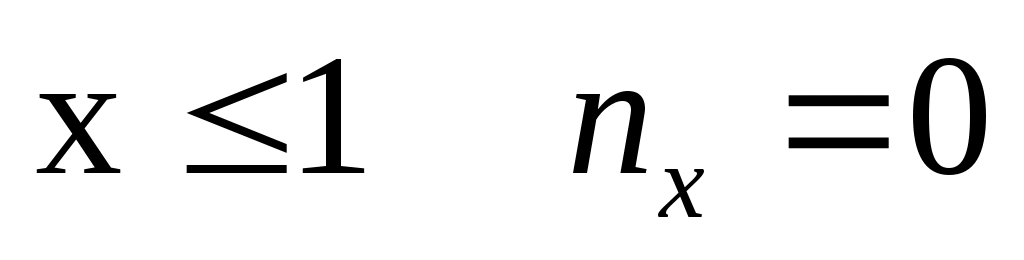 , оскільки найменша варіанта х1=1. Тому , оскільки найменша варіанта х1=1. Тому 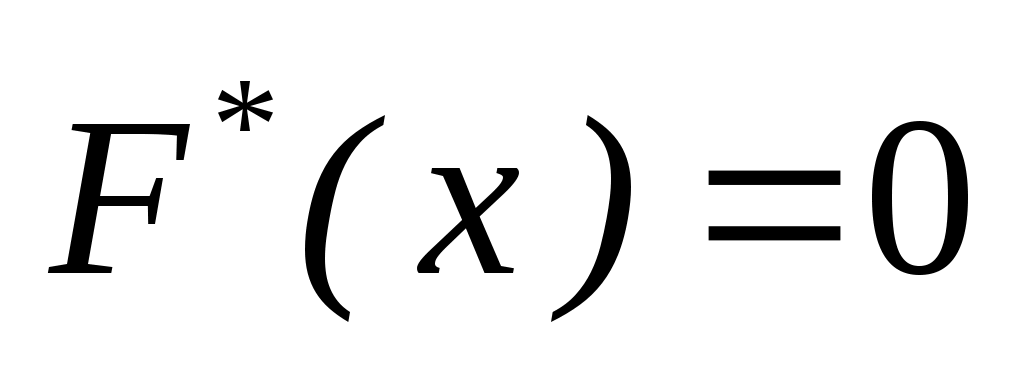 , при , при 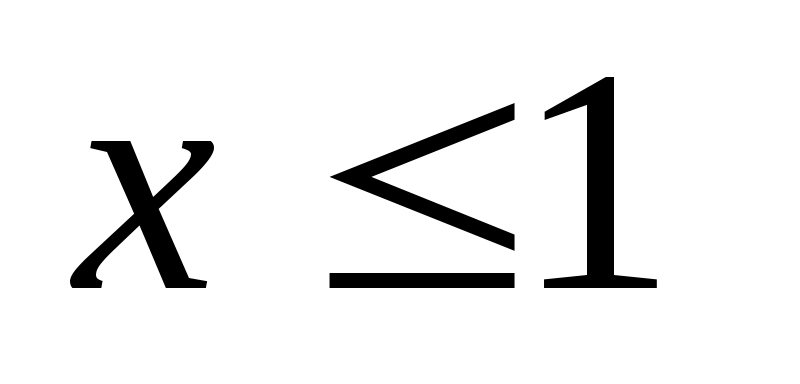 . .
При 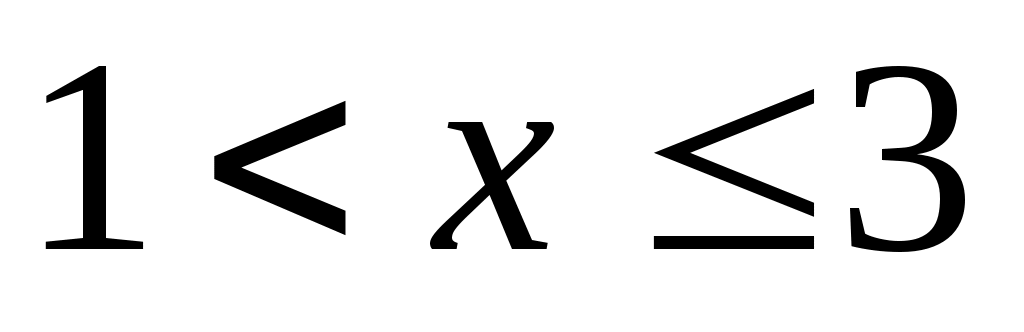 лише варіанта х1=1< х, причому лише варіанта х1=1< х, причому 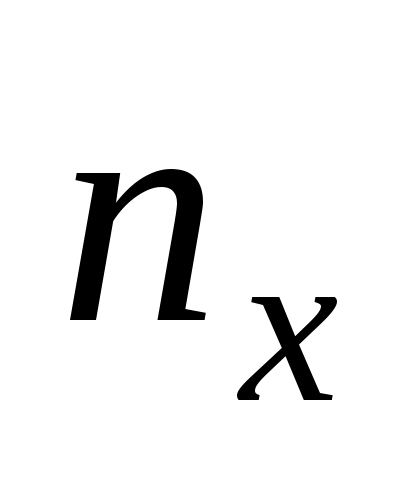 =4. Тому =4. Тому 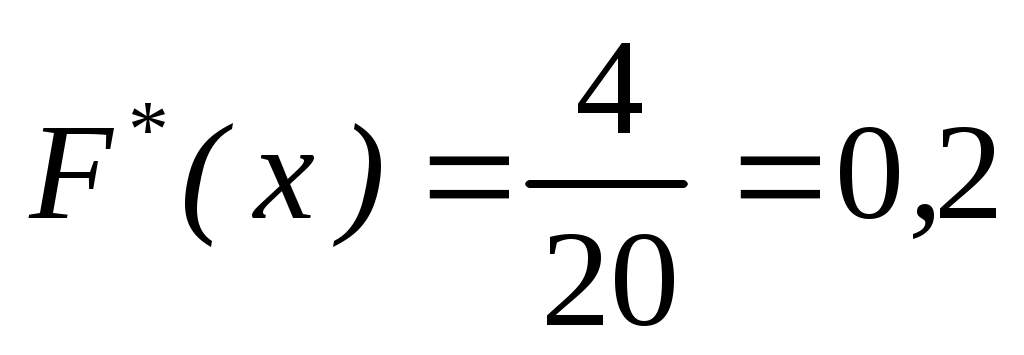 , при , при 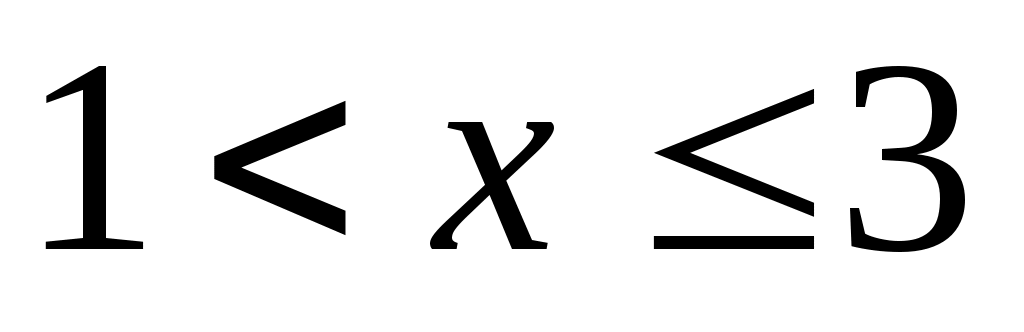 . .
При 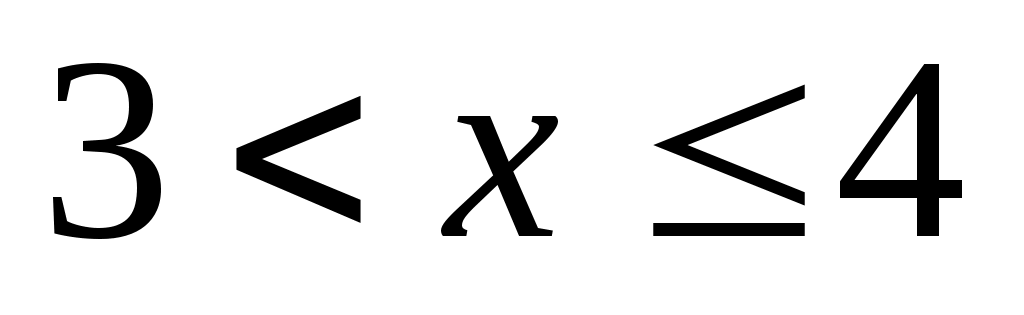 варіанти х1 =1 і х2 =3 менші х, причому варіанти х1 =1 і х2 =3 менші х, причому 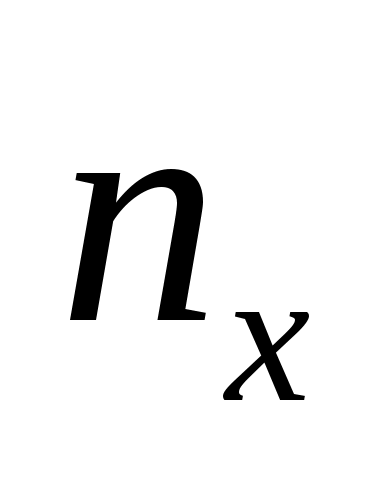 =4+8=12. Тому =4+8=12. Тому 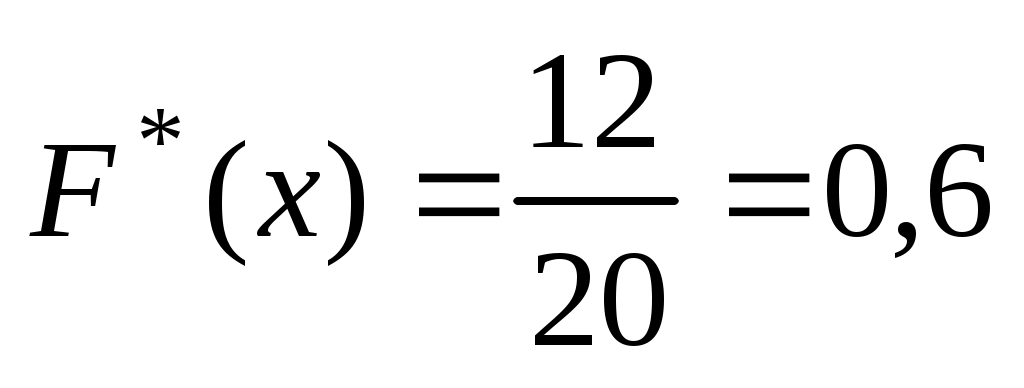 при при 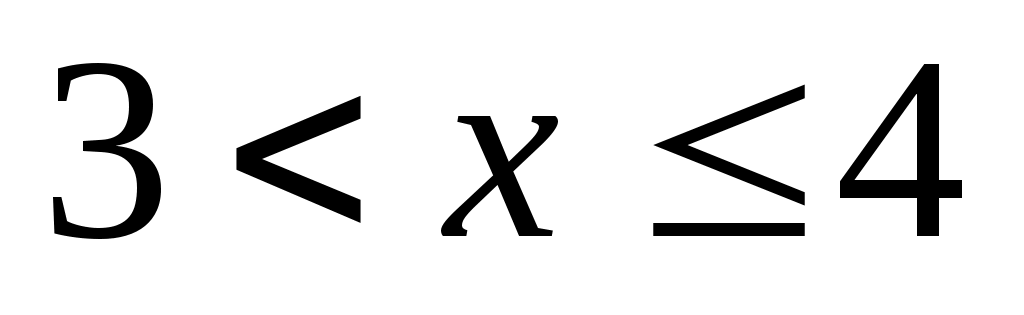 . .
При 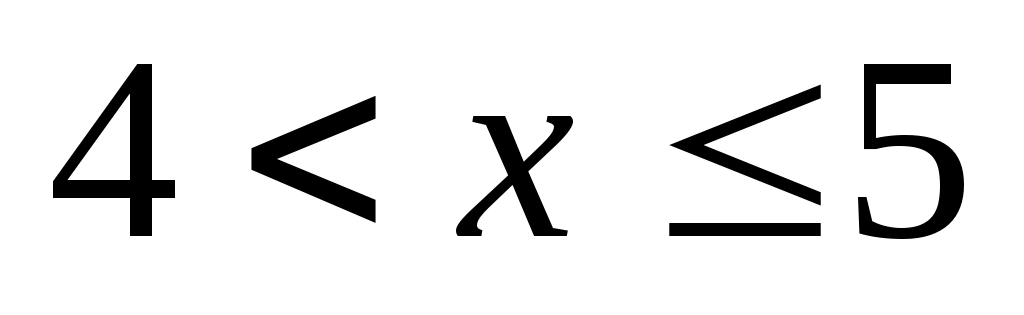 варіанти х1 =1, х2 =2 і х3 =4 менші х, причому варіанти х1 =1, х2 =2 і х3 =4 менші х, причому 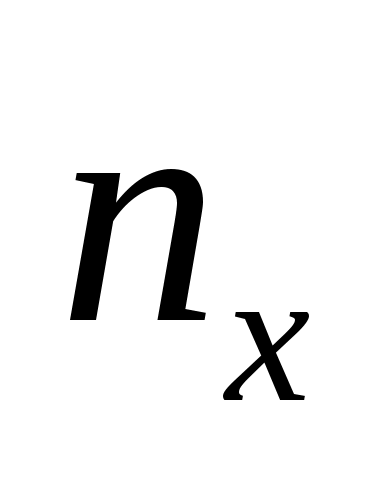 =4+8+6=18. Тому =4+8+6=18. Тому 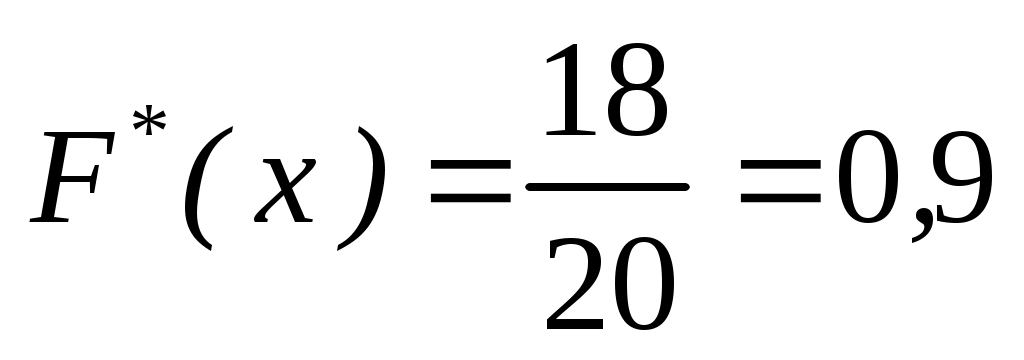 при при 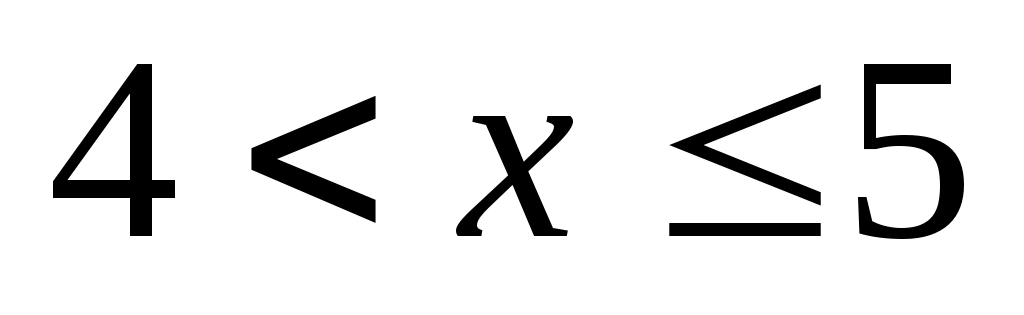 . .
При x >5 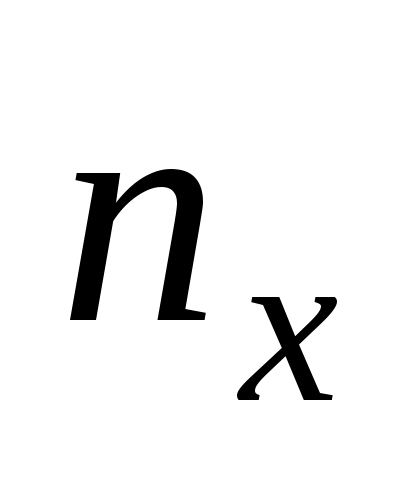 =20 і отже =20 і отже 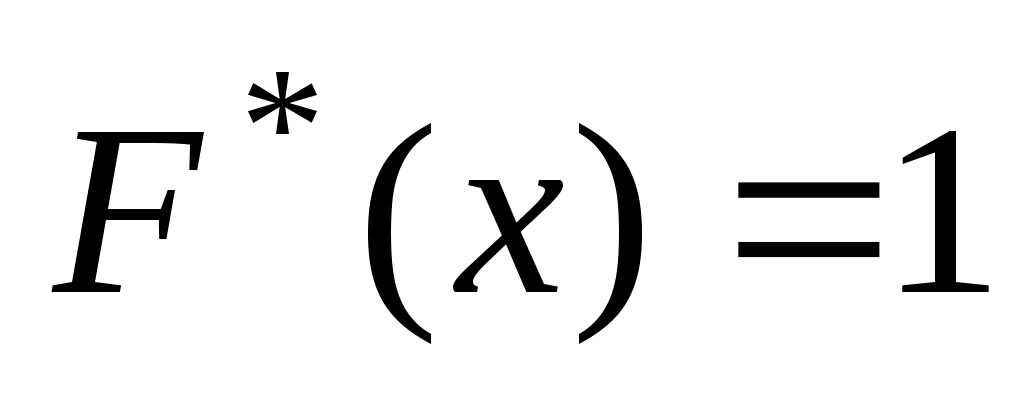 . .
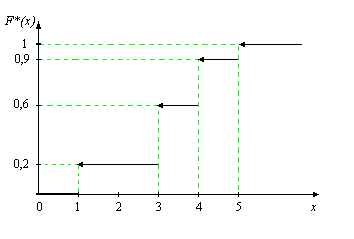
Таким чином емпірична функція розподілу має вигляд:
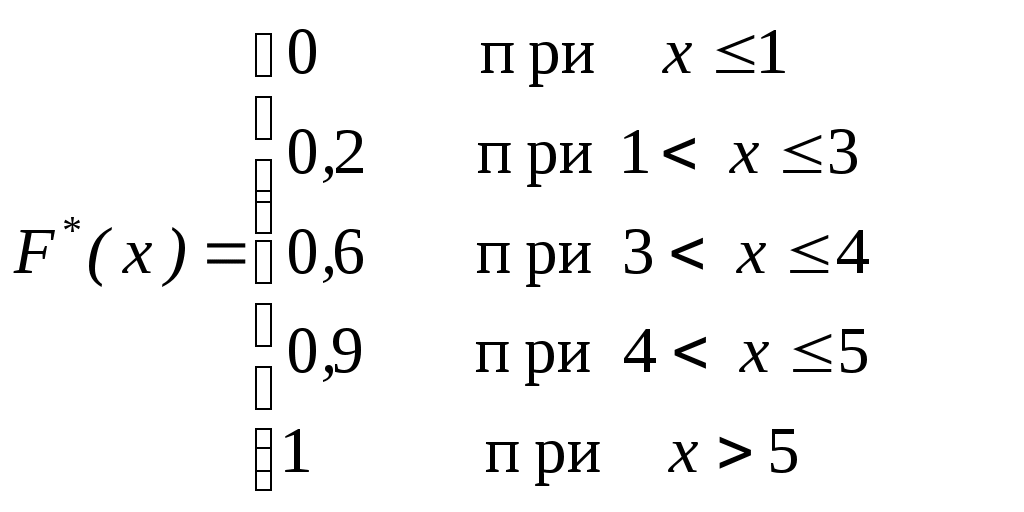 . .
Будуємо графік цієї функції.
Приклад 2. Дано інтервальний варіаційний ряд

|
1-3
|
3-5
|
5-7
|
7-9
|
9-11
|
ni
|
7
|
10
|
20
|
8
|
5
|
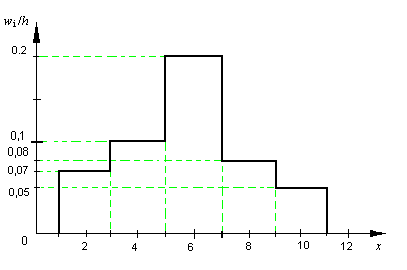
Побудувати гістограму відносних частот.
Розв’язання. Об’єм вибірки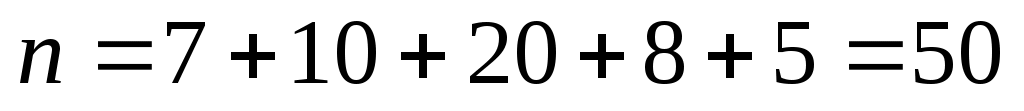 , довжина часткового інтервалу h =2. , довжина часткового інтервалу h =2.
Знаходимо щільності відносних частот wi за формулою 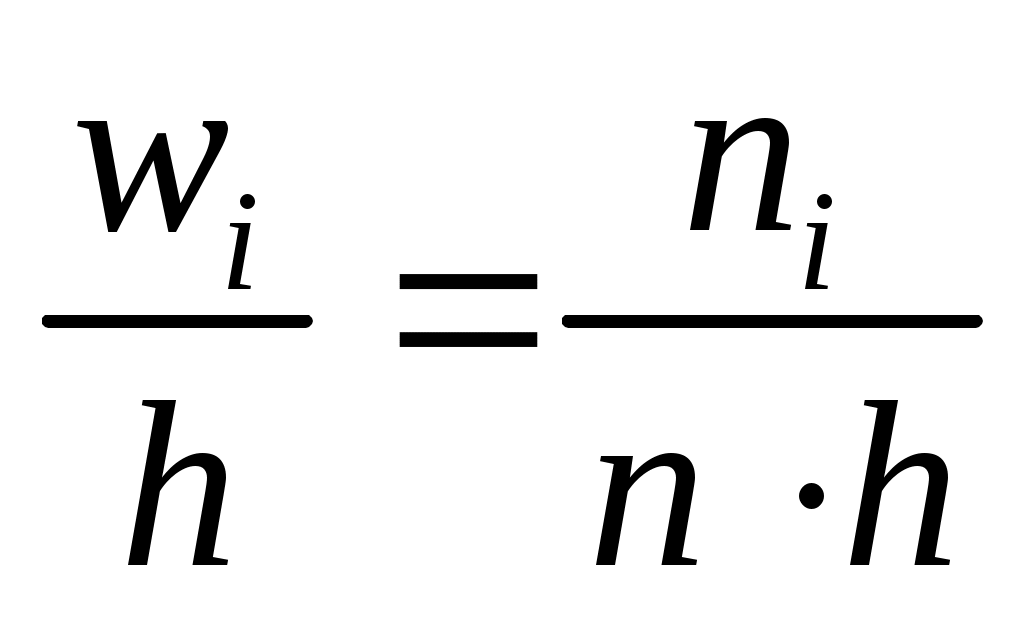 : :
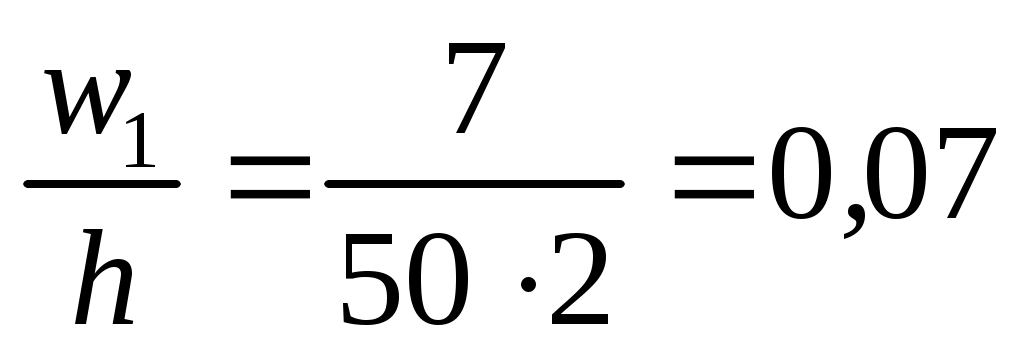 ; ; 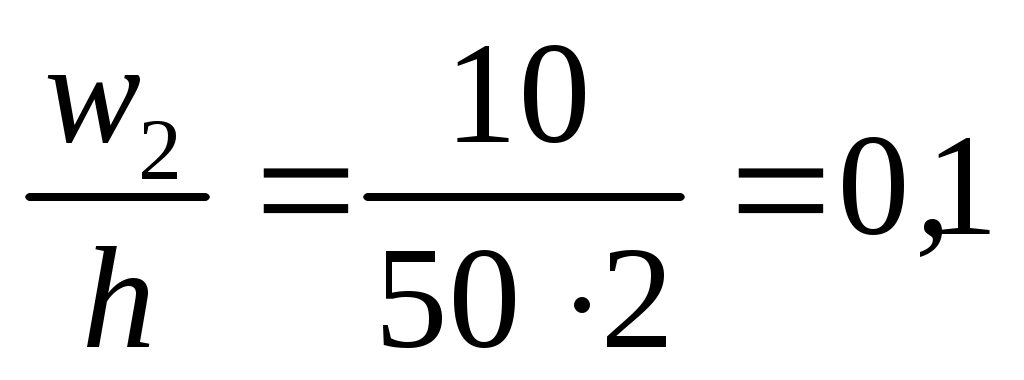 ; ; 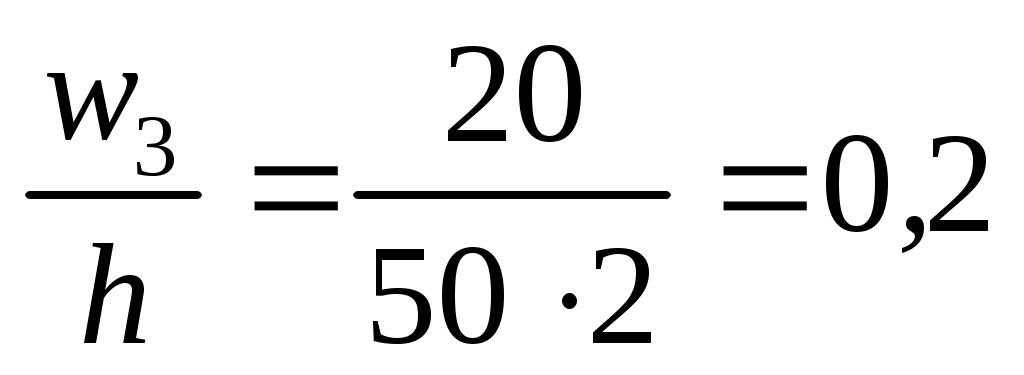 ; ; 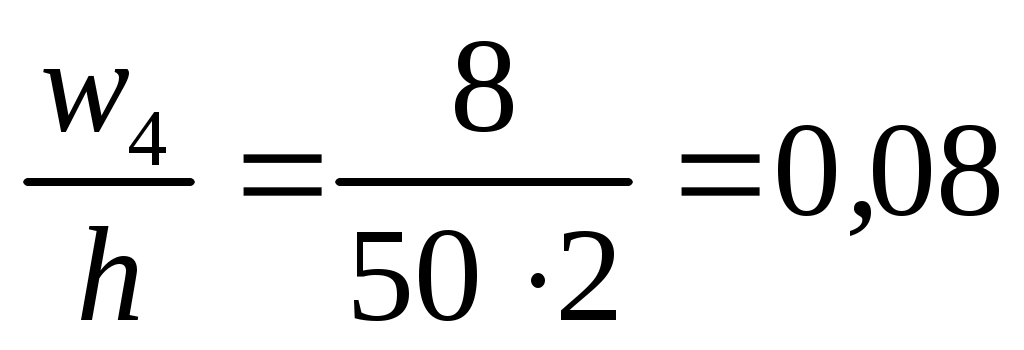 ; ; 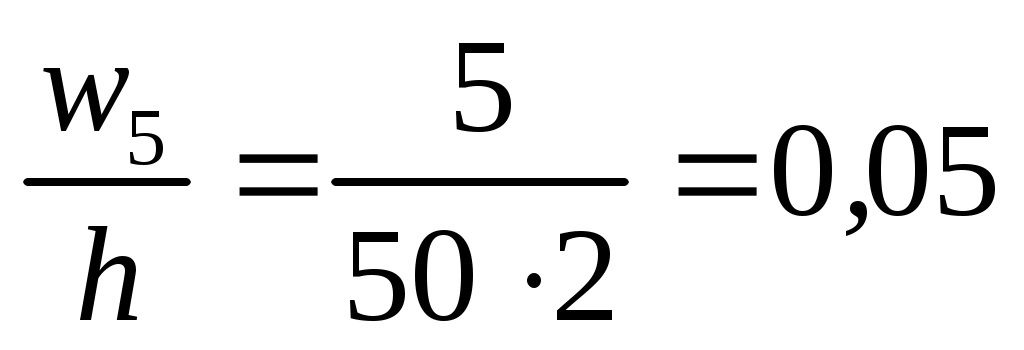 . .
Відкладемо на осі абсцис часткові інтервали  і проведемо над цими інтервалами відрізки, які паралельні осі абсцис і знаходяться від неї на відстанях рівних відповідно wi /h. Отримаємо шукану гістограму відносних частот. і проведемо над цими інтервалами відрізки, які паралельні осі абсцис і знаходяться від неї на відстанях рівних відповідно wi /h. Отримаємо шукану гістограму відносних частот.
Приклад 3.
1) Задано статистичний розподіл вибірки
Знайти вибіркове середнє 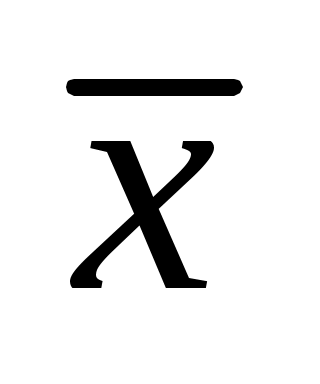 , вибіркову дисперсію , вибіркову дисперсію 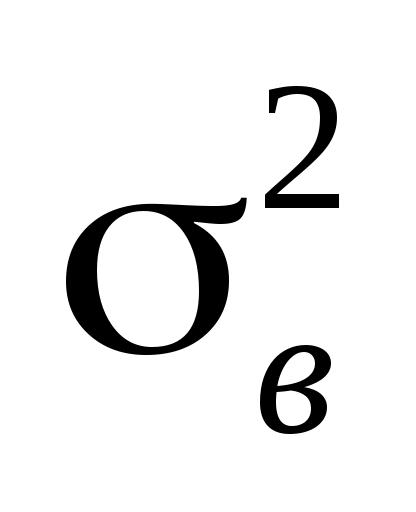 , виправлену вибіркову дисперсію , виправлену вибіркову дисперсію 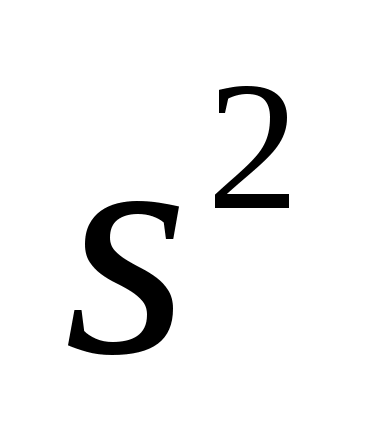 і вибіркове середнє квадратичне відхилення і вибіркове середнє квадратичне відхилення 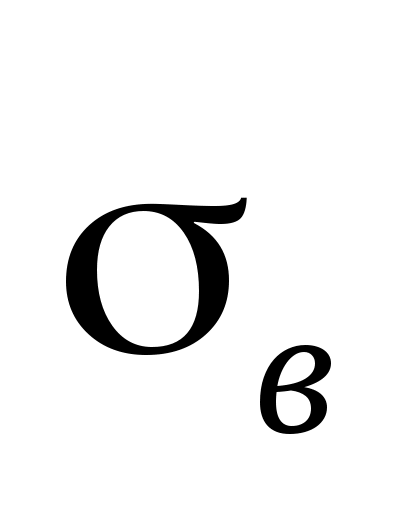 . .
2) Задано інтервальний варіаційний ряд

|
2-4
|
4-6
|
6-8
|
8-10
|
10-12
|
ni
|
42
|
73
|
154
|
205
|
26
|
Знайти вибіркове середнє 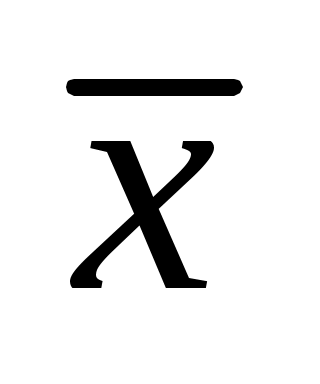 та вибіркову дисперсію та вибіркову дисперсію 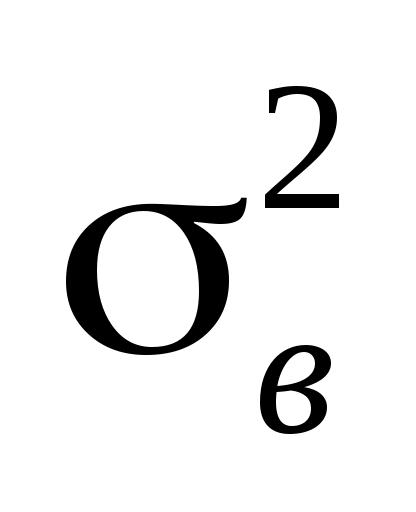 . .
Розв’язання. 1) Об’єм вибірки n =2+3+4+1=10.
Вибіркове середнє 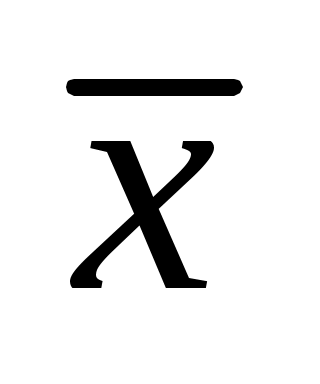 знаходимо за формулою: знаходимо за формулою: 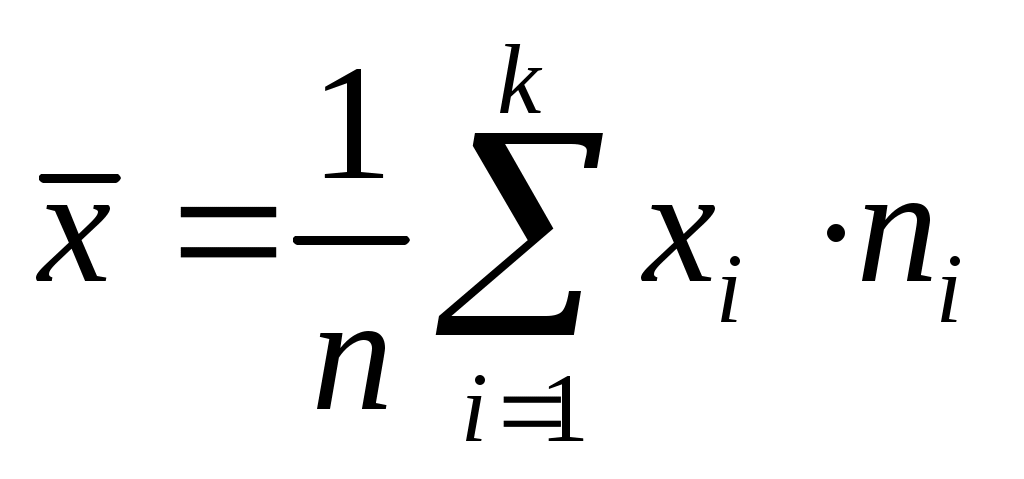 . .
Отримаємо :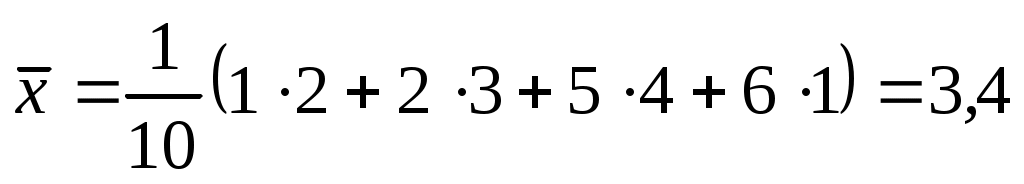 . .
Вибіркову дисперсію знаходимо за формулою:
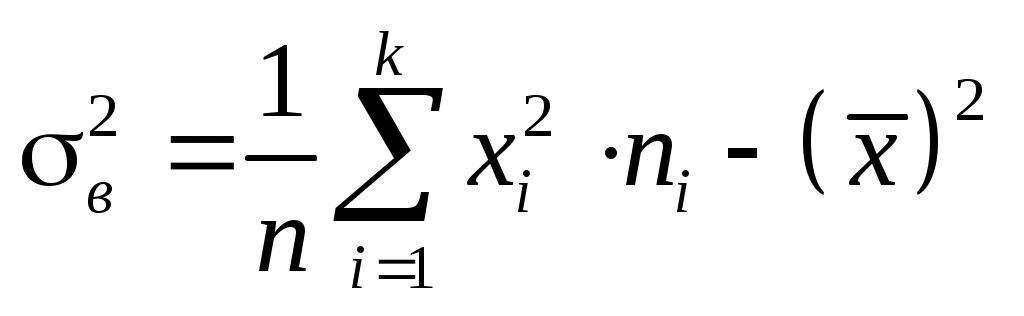 . .
Отримаємо: 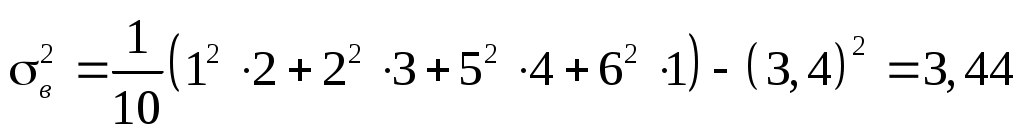 . .
Знаходимо 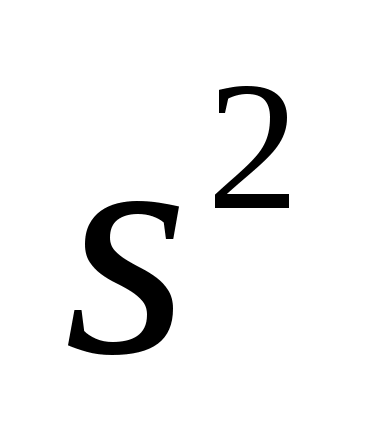 та та 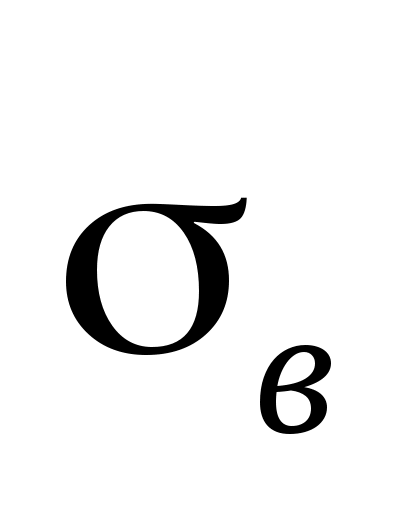 : : 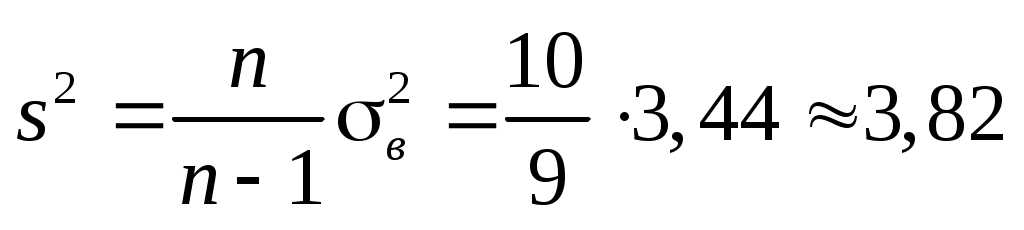 , ,
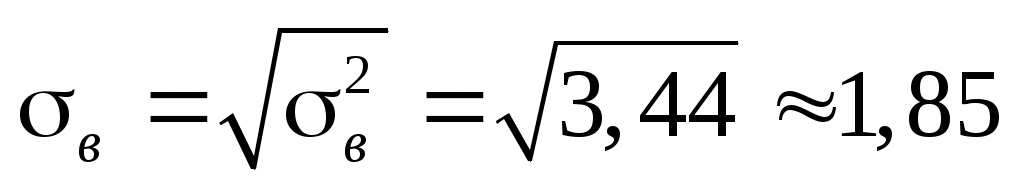 . .
2) Знаходимо середини часткових інтервалів: х1=3, х2=5, х3=7, х4=9, х5=11. За формулами отримаємо: 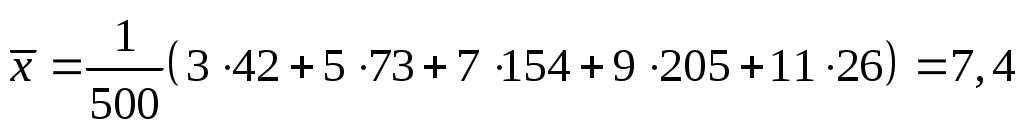 ; ;
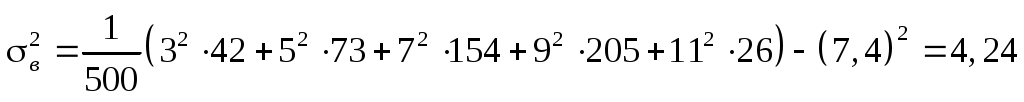 . .
Приклад 4. Побудувати надійний інтервал для оцінки з надійністю 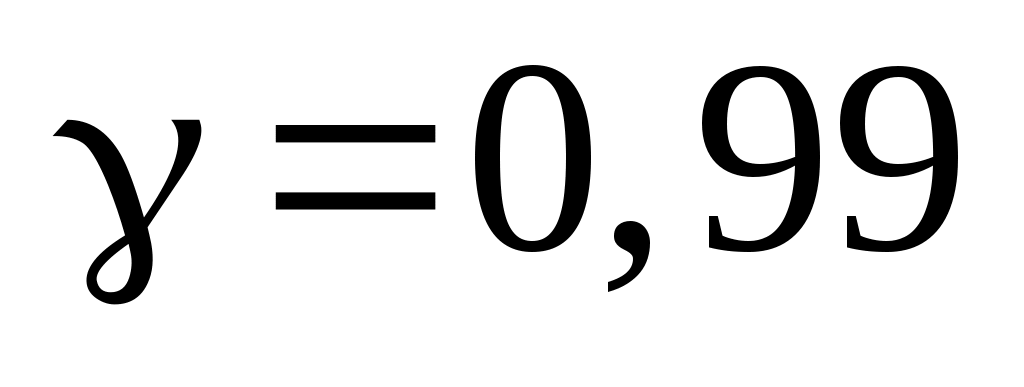 невідомого математичного сподівання невідомого математичного сподівання  нормально розподіленої генеральної сукупності Х, якщо нормально розподіленої генеральної сукупності Х, якщо 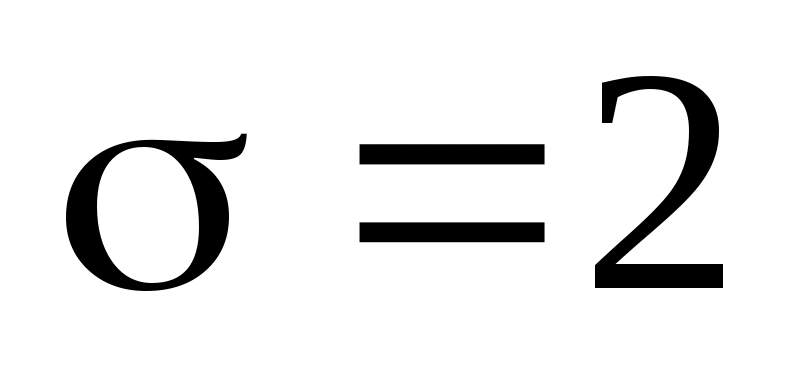 , ,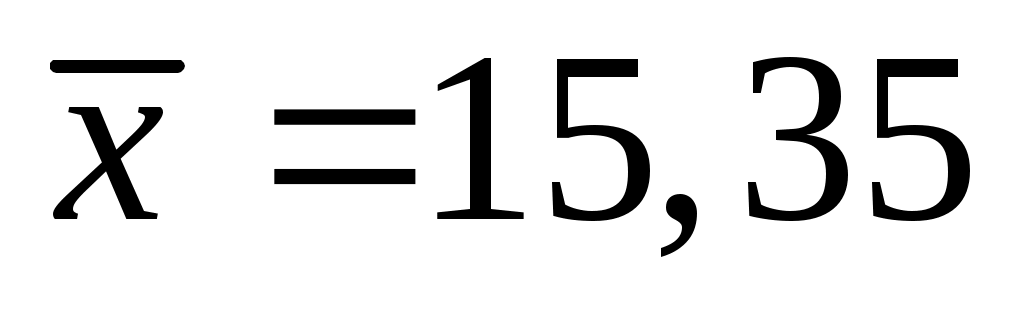 і і 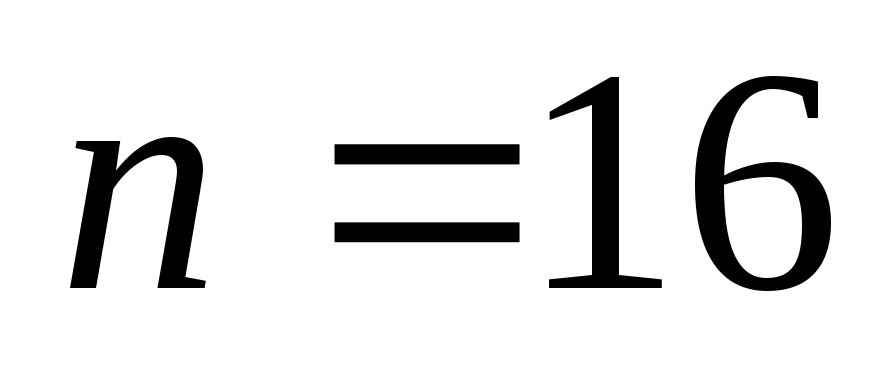 . .
Розв’язання. Шуканий надійний інтервал має вигляд
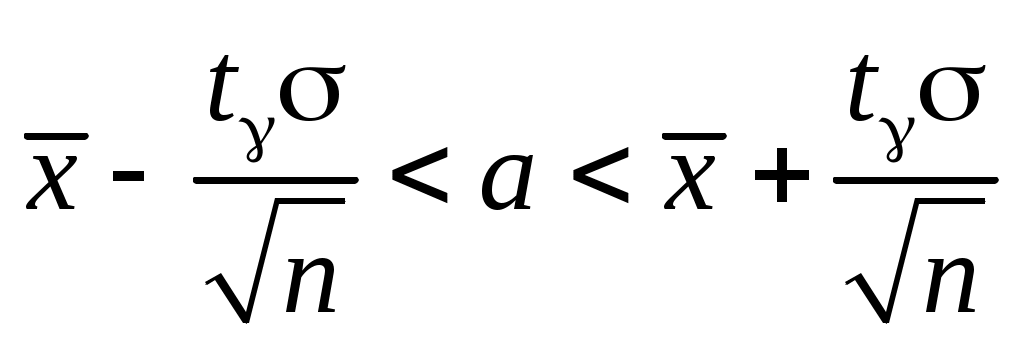 , ,
|
(1)
|
де 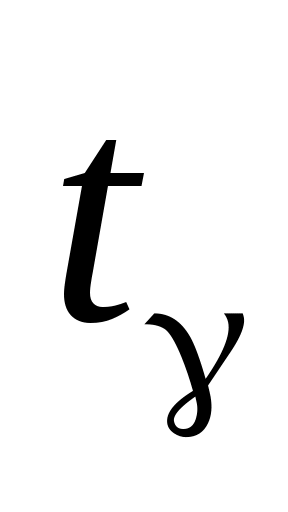 – значення аргументу функції Лапласа – значення аргументу функції Лапласа 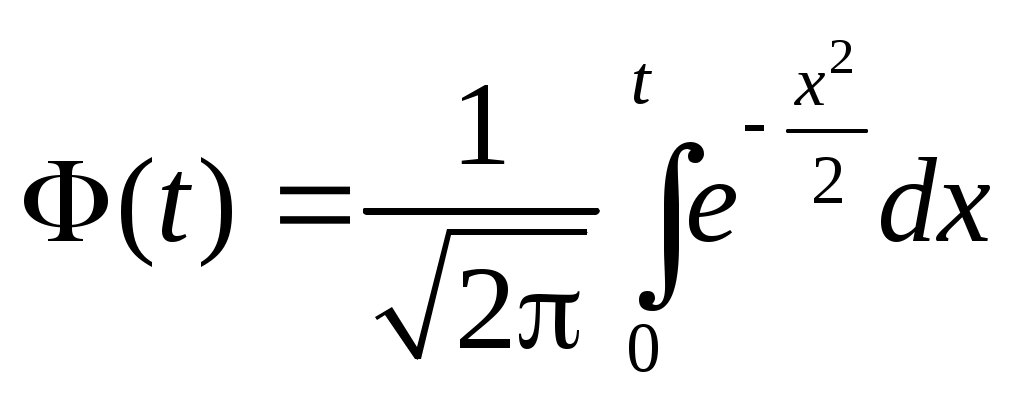 , при якому , при якому 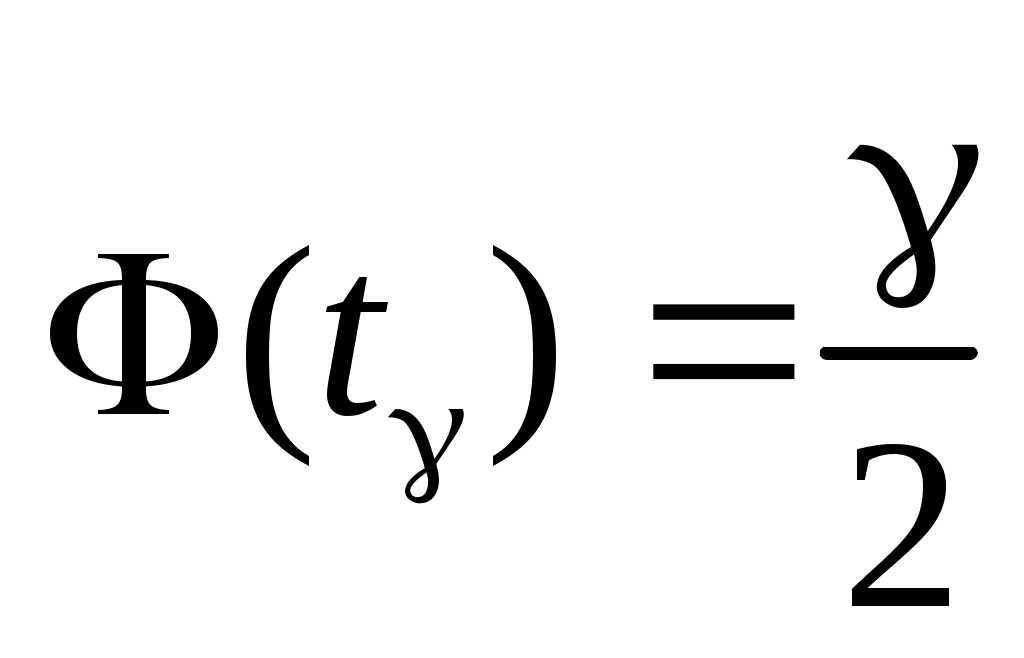 . Знаходимо . Знаходимо 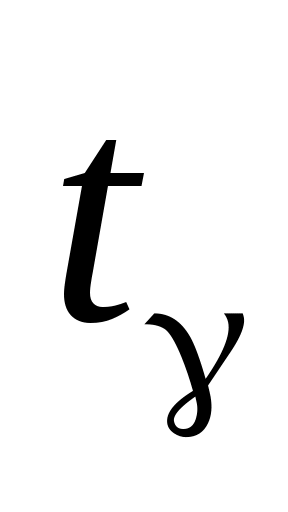 із співвідношення із співвідношення 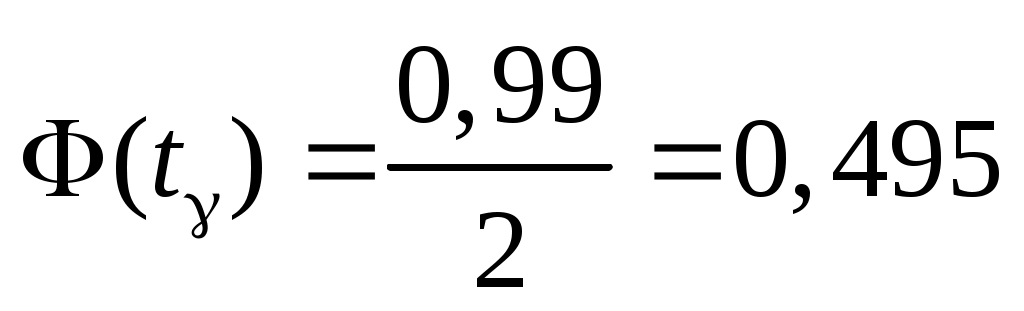 . .
За таблицею значень функції Лапласа знаходимо 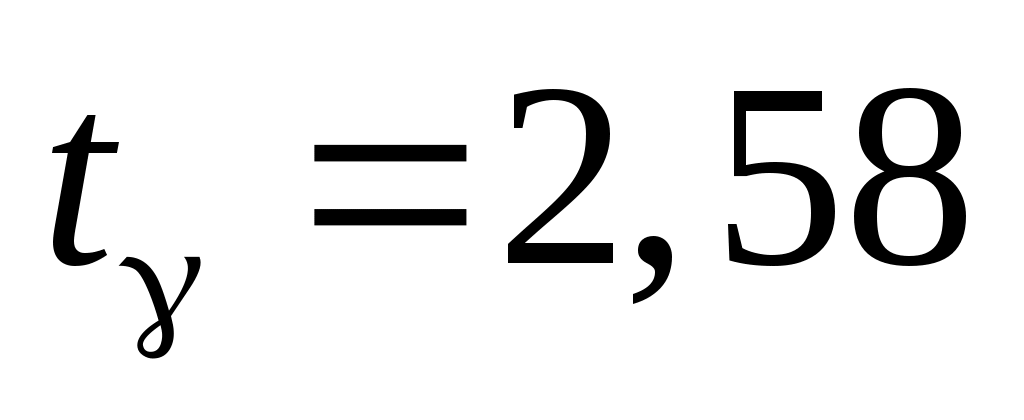 . Підставляючи . Підставляючи 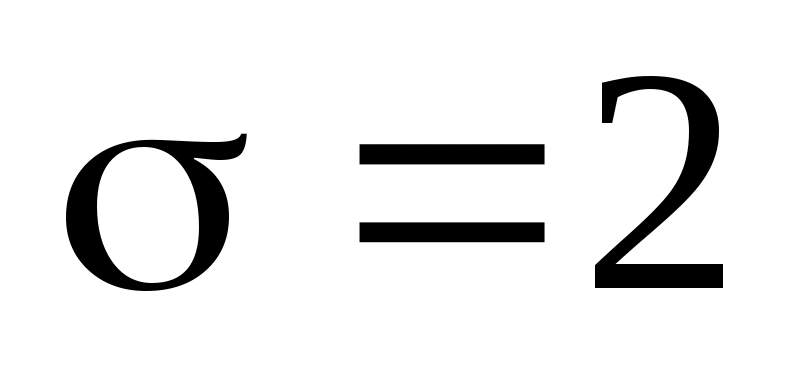 , , 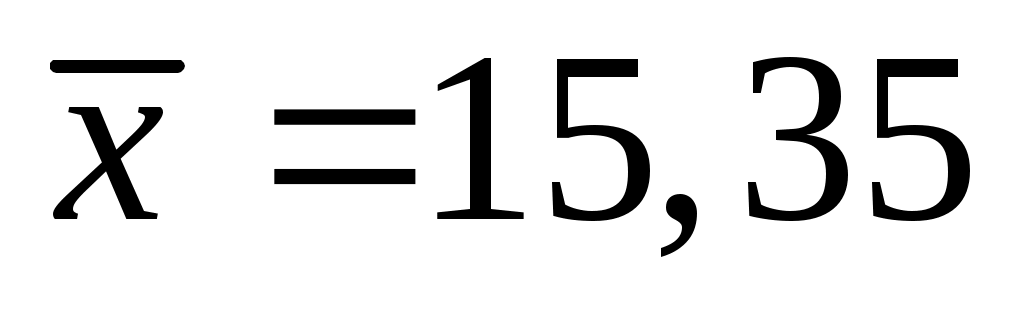 , , 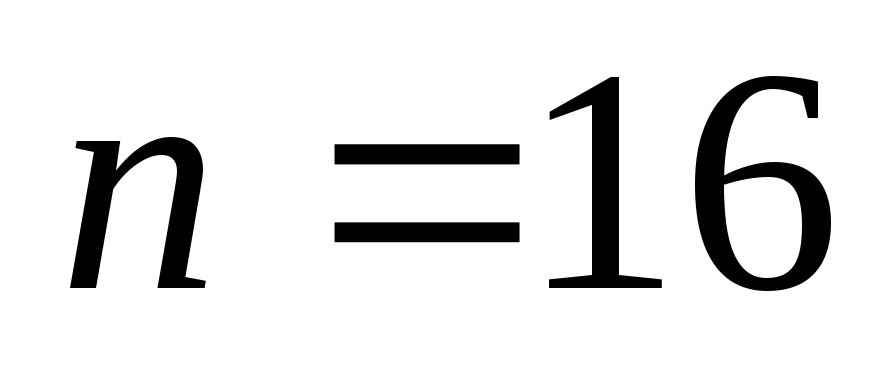 , , 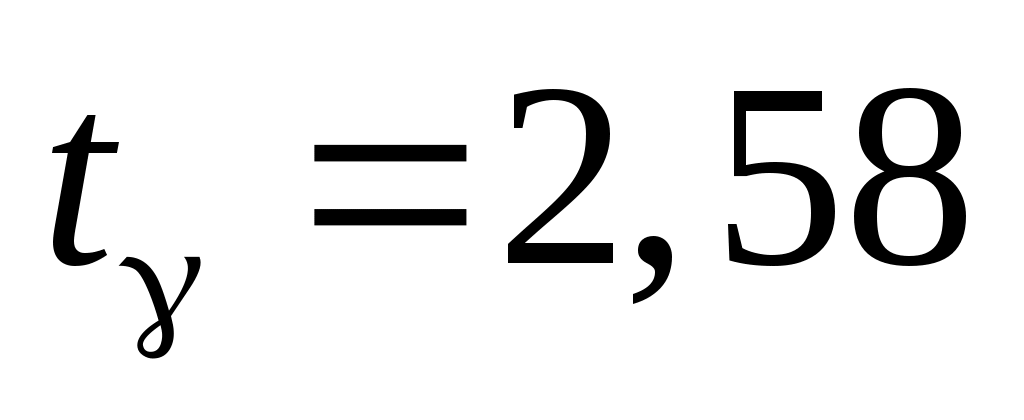 в (1), отримаємо надійний інтервал: 14,06 в (1), отримаємо надійний інтервал: 14,06  16,64. 16,64.
Приклад 5. Побудувати надійний інтервал для оцінки з надійністю 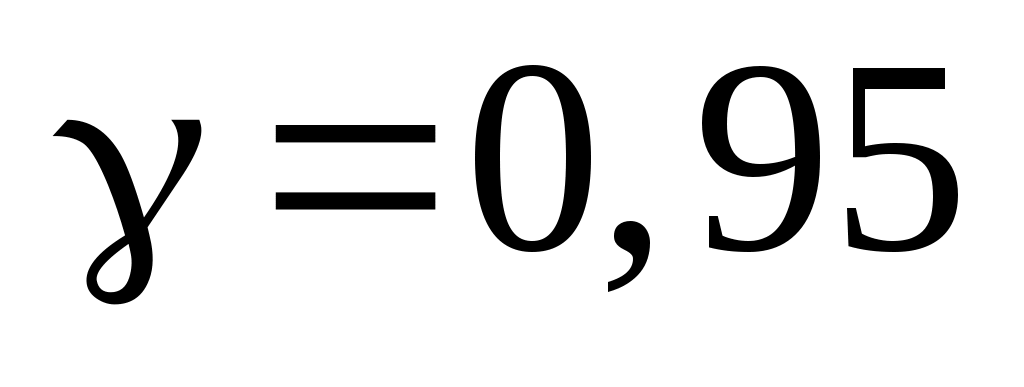 невідомого середнього квадратичного відхилення невідомого середнього квадратичного відхилення 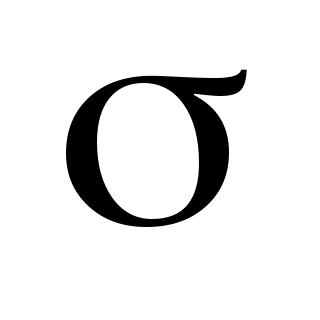 нормально розподіленої генеральної сукупності Х, якщо нормально розподіленої генеральної сукупності Х, якщо 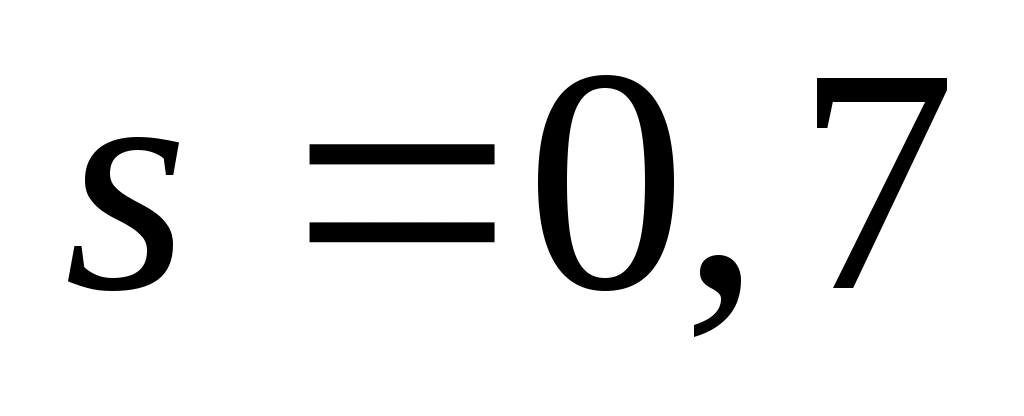 і і 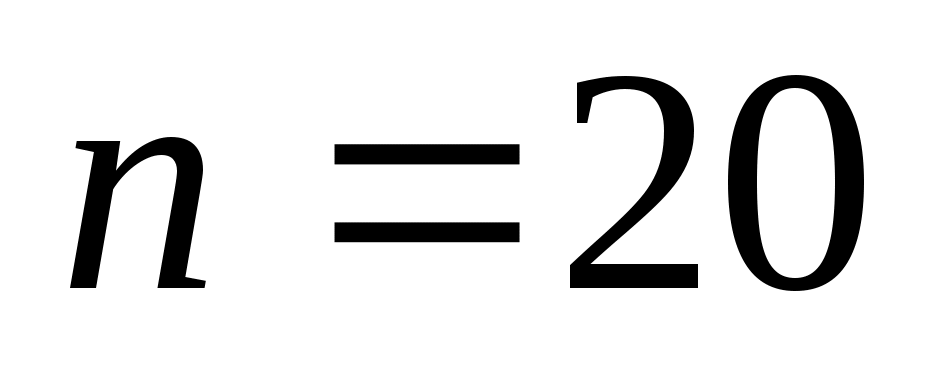 . .
Розв’язання. Шуканий надійний інтервал має вигляд:
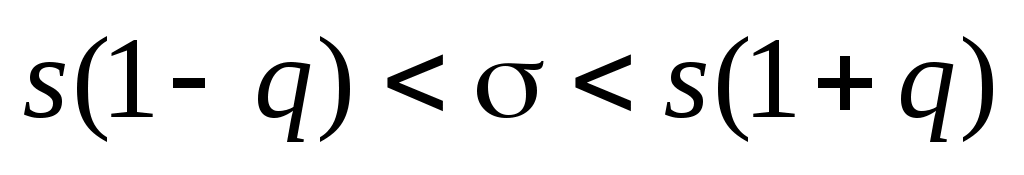 , при q1; , при q1;
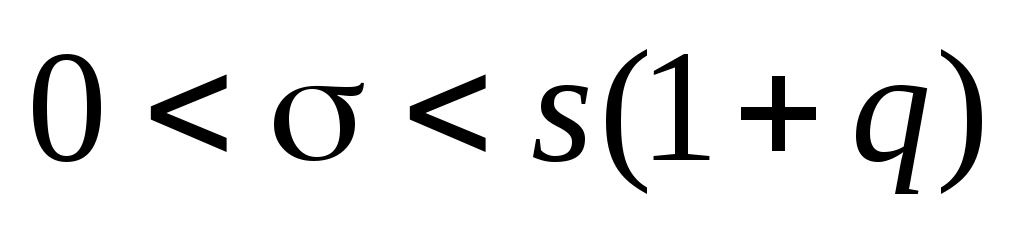 , при q1; , при q1;
|
(2)
|
де 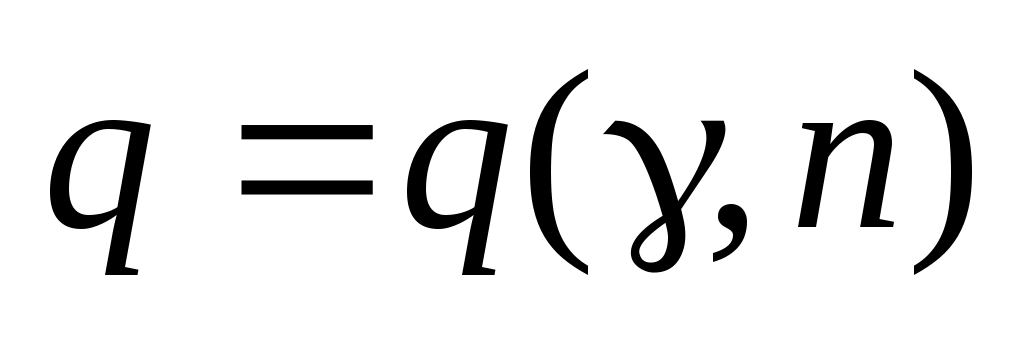 знаходиться за таблицею по заданих знаходиться за таблицею по заданих 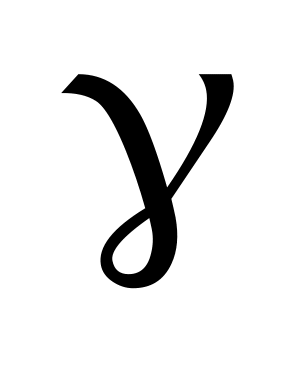 і і 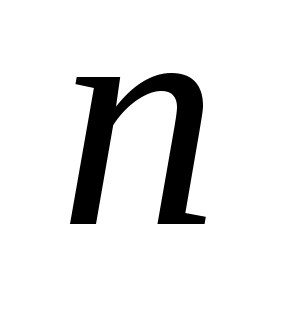 . При . При 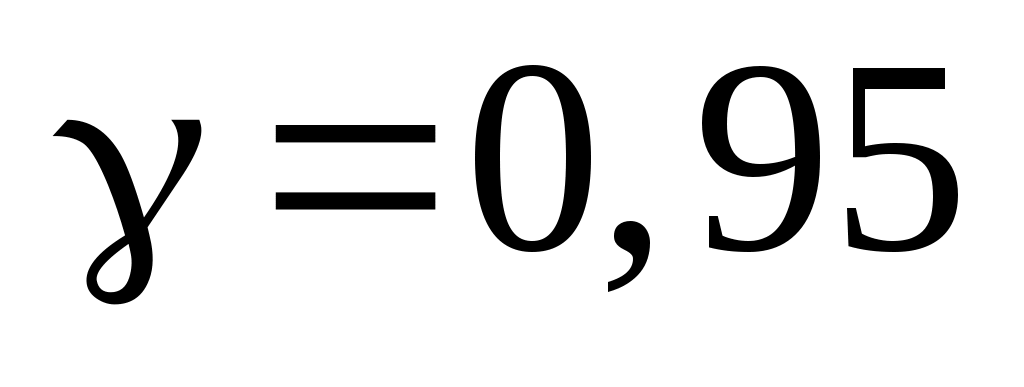 і і 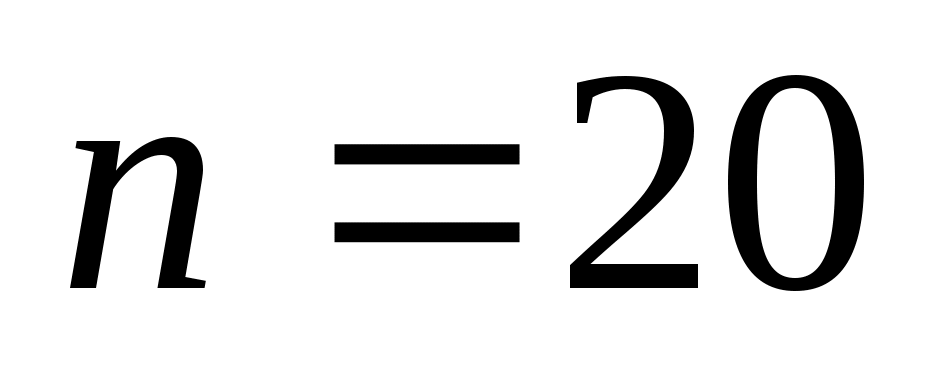 за таблицею знаходимо q =0,37. за таблицею знаходимо q =0,37.
Підставляючи 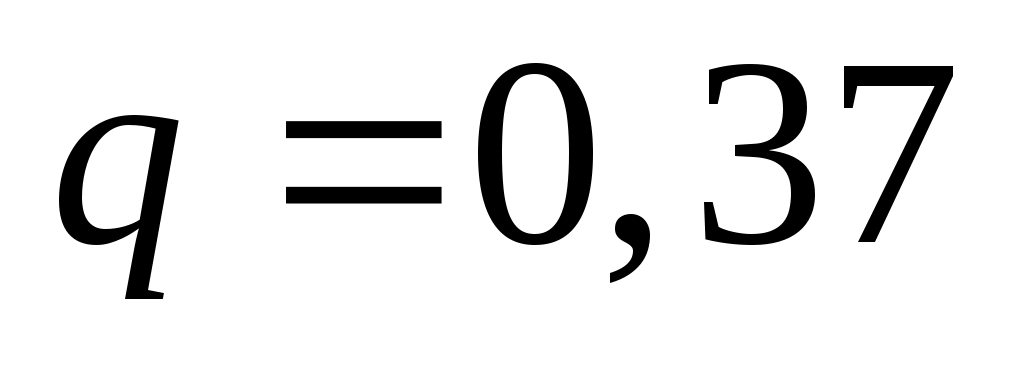 , , 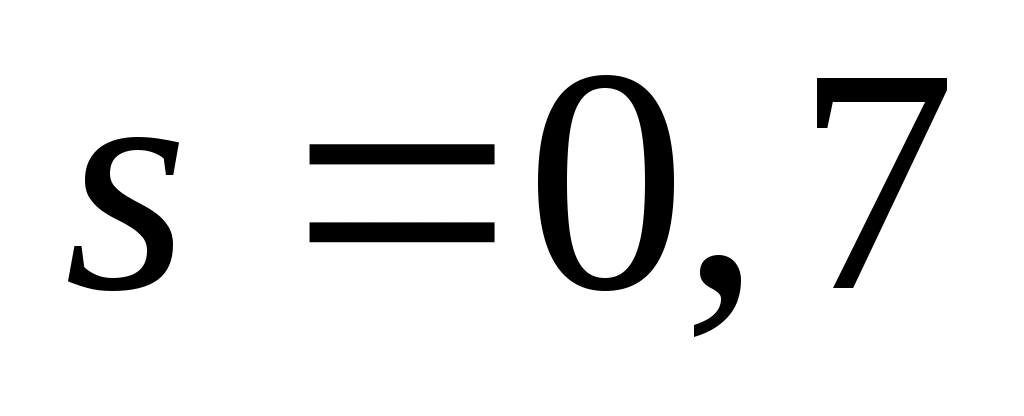 , , 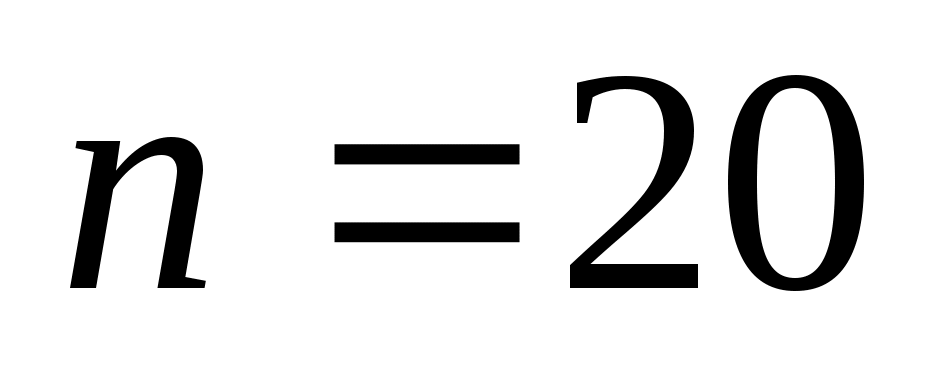 в (2), отримаємо надійний інтервал: 0,441 в (2), отримаємо надійний інтервал: 0,441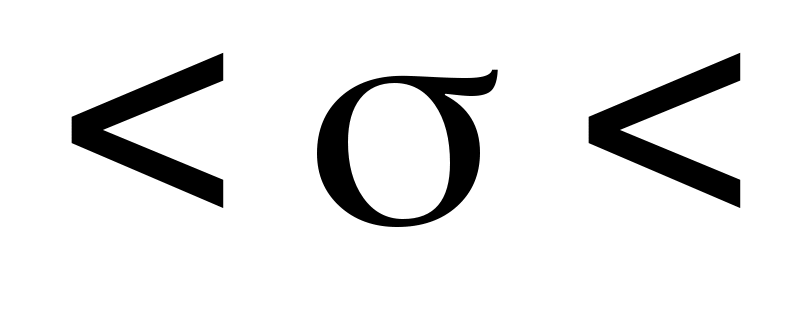 , ,
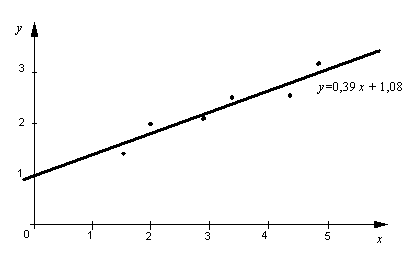
Приклад 6. Знайти вибіркове рівняння прямої регресії 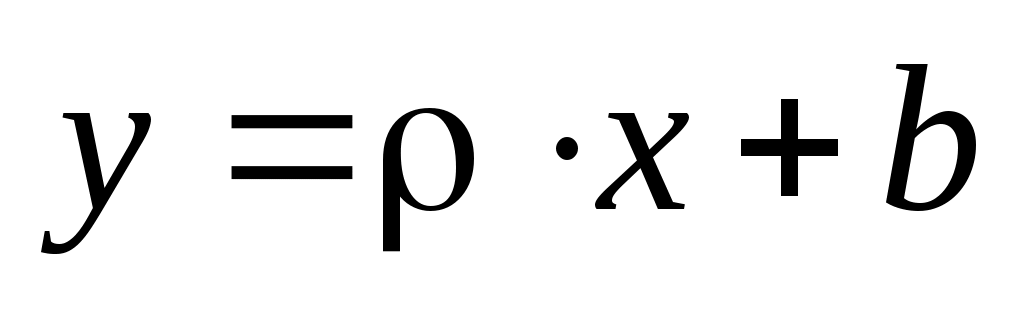 за даними шести спостережень (xi ; yi): (1,5;1,3), (2;2), (3;2,1), (3,5;2,7), (4,5;2,6), (5;3,3). Зробити малюнок, на якому вказати експериментальні дані та побудувати пряму регресії. за даними шести спостережень (xi ; yi): (1,5;1,3), (2;2), (3;2,1), (3,5;2,7), (4,5;2,6), (5;3,3). Зробити малюнок, на якому вказати експериментальні дані та побудувати пряму регресії.
Розв’язання. Невідомі параметри регресії 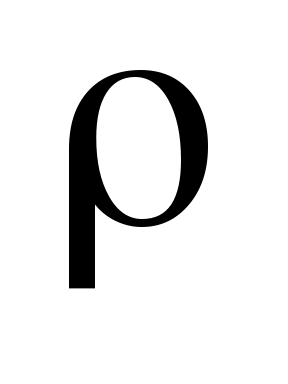 і b знаходять із системи рівнянь і b знаходять із системи рівнянь
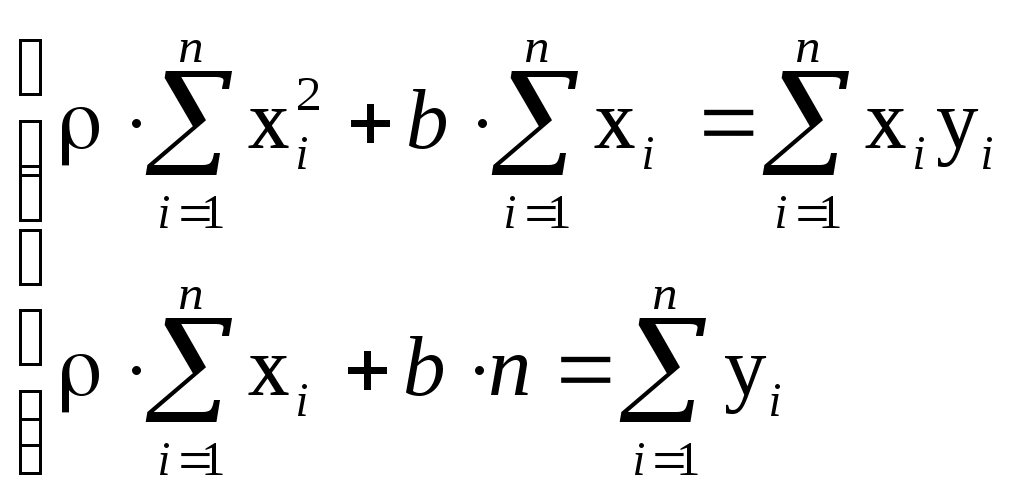 . .
|
(3)
|
З умови задачі знаходимо: 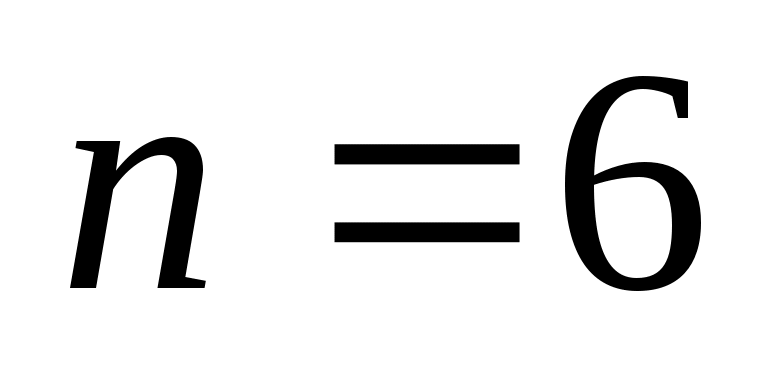 , , 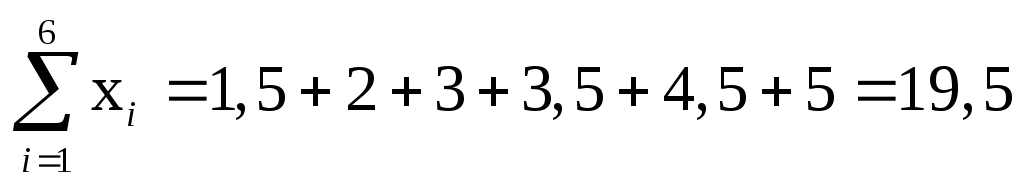 , , 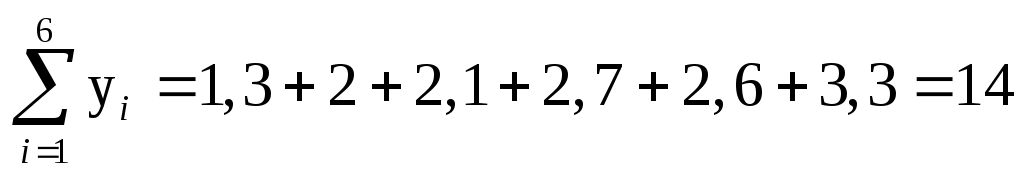 , , 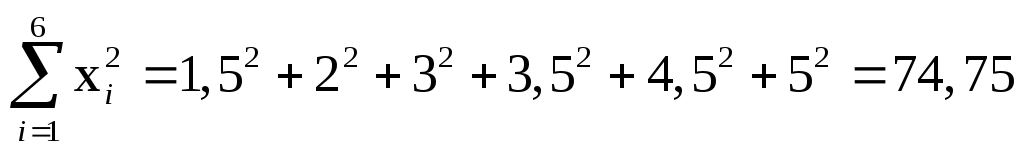 , , 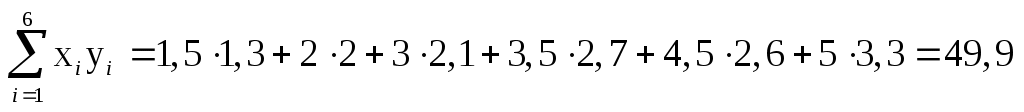 , ,
Підставляючи в (3), отримаємо систему:
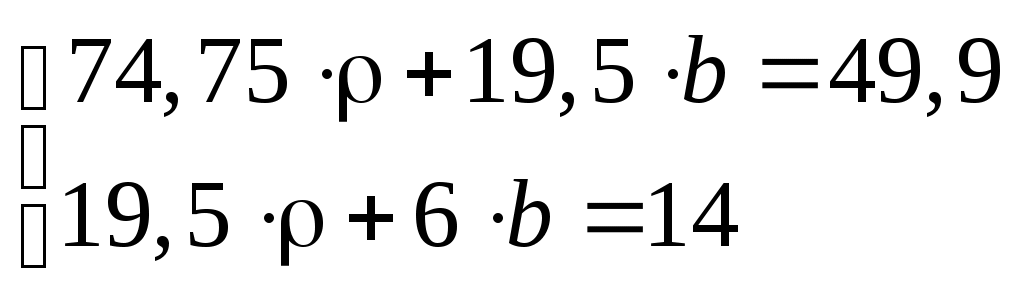 . .
Звідки, розв’язуючи систему, отримаємо 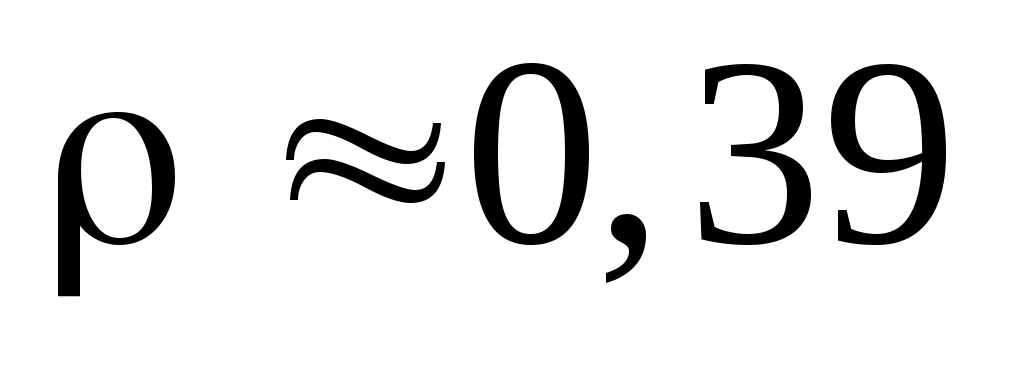 і і 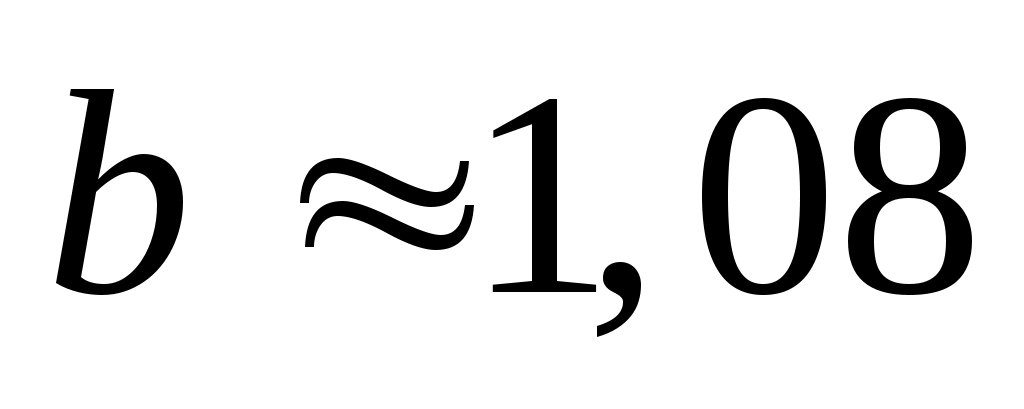 . .
Запишемо шукане рівняння прямої лінії регресії:
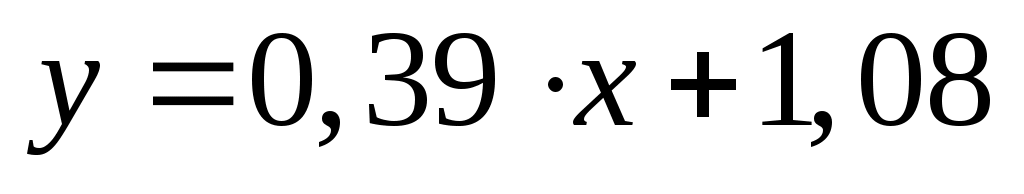 . .
Зробимо малюнок, на якому вкажемо експериментальні дані та побудуємо пряму лінію регресії.
Приклад 7. Використовуючи критерій Пірсона, при рівні значущості 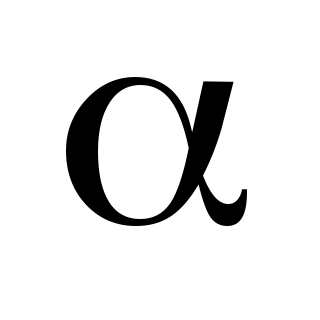 перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х з статистичними даними, які подані у вигляді інтервального варіаційного ряду (в першому рядку вказано часткові інтервали перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х з статистичними даними, які подані у вигляді інтервального варіаційного ряду (в першому рядку вказано часткові інтервали  , в другому – відповідні їм частоти , в другому – відповідні їм частоти  ). ).
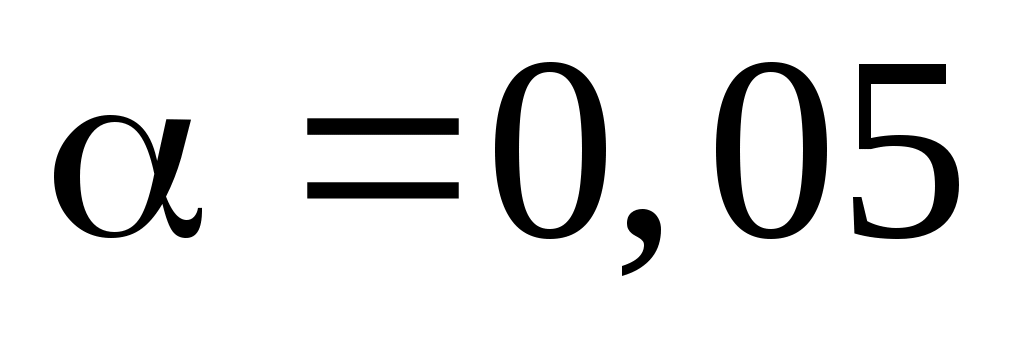 ; ;

|
–20-(–10)
|
–10-0
|
0-10
|
10-20
|
20-30
|
30-40
|
40-50
|

|
20
|
47
|
80
|
89
|
40
|
16
|
8
|
Розв’язання. Знайдемо середини часткових інтервалів 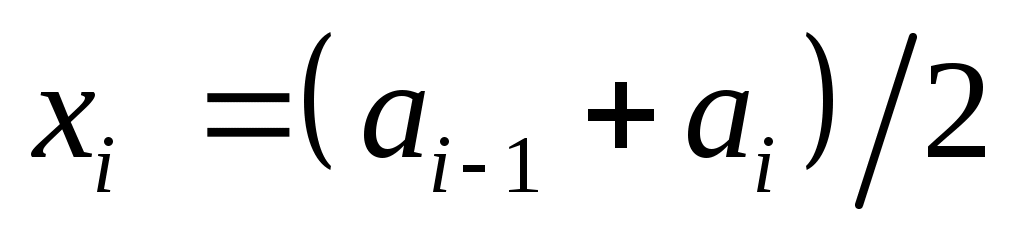 та складемо таблицю та складемо таблицю
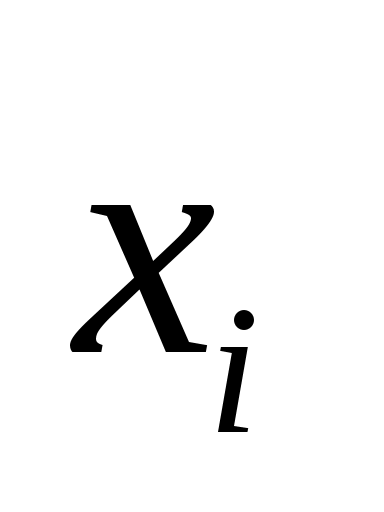
|
–15
|
–5
|
5
|
15
|
25
|
35
|
45
|

|
20
|
47
|
80
|
89
|
40
|
16
|
8
|
Обчислимо вибіркове середнє 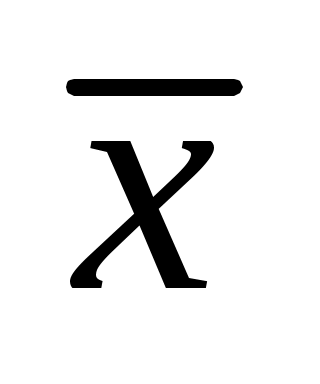 та вибіркове середнє квадратичне відхилення та вибіркове середнє квадратичне відхилення 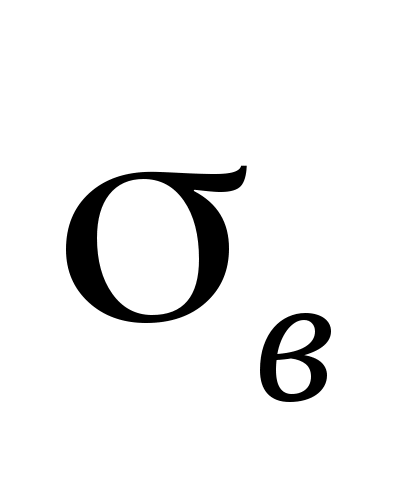 (див. приклад 3, КР № 2.): (див. приклад 3, КР № 2.):
об’єм вибірки 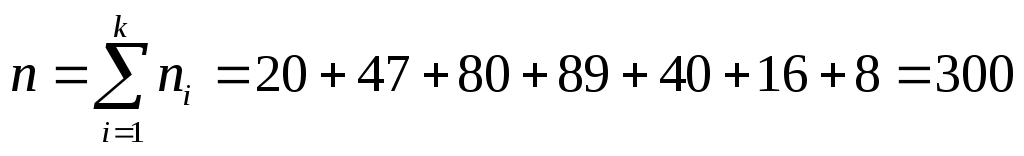 ; ;
вибіркове середнє 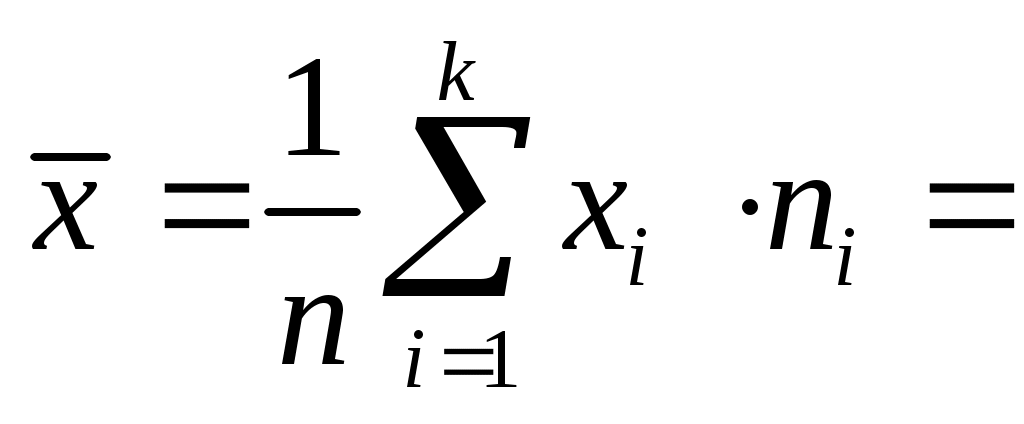 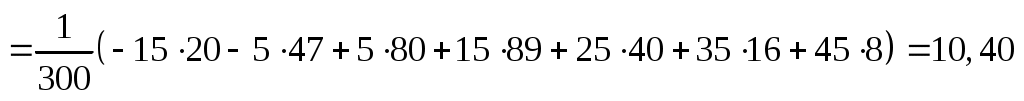 ; ;
вибіркова дисперсія 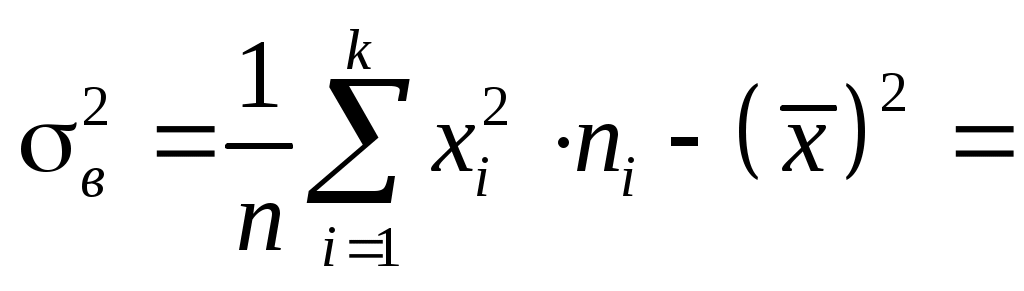
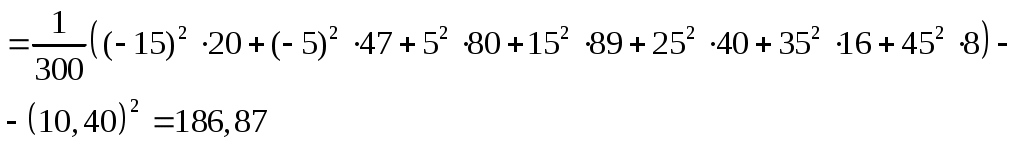 і вибіркове середнє квадратичне відхилення і вибіркове середнє квадратичне відхилення 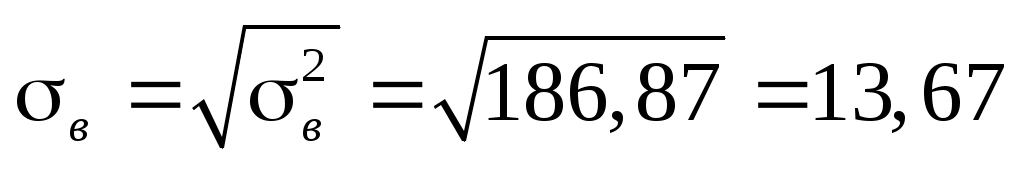 . .
Перейдемо до випадкової величини 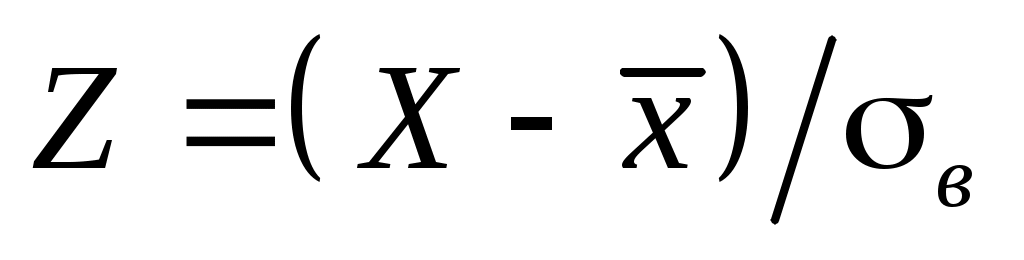 та обчислимо кінці інтервалів та обчислимо кінці інтервалів 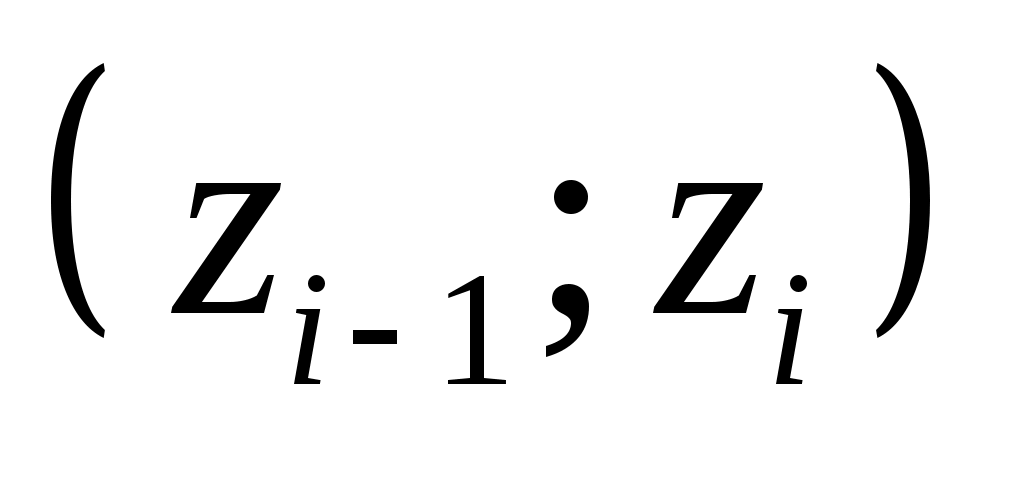 : : 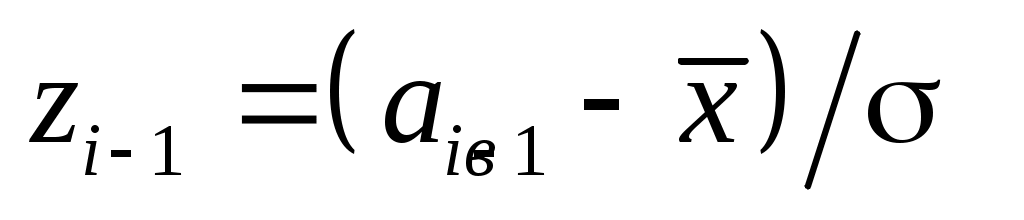 ; ; 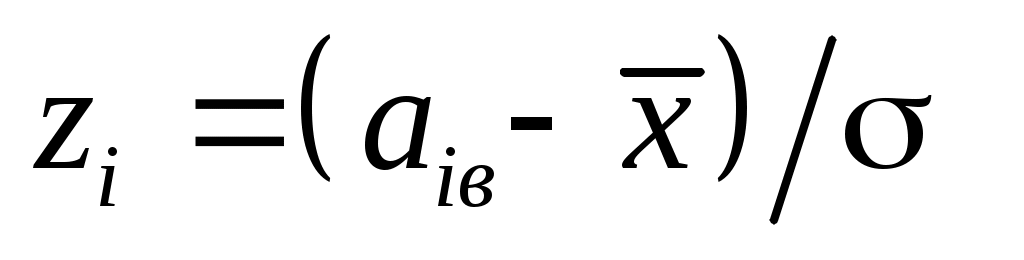 , причому найменше значення , причому найменше значення 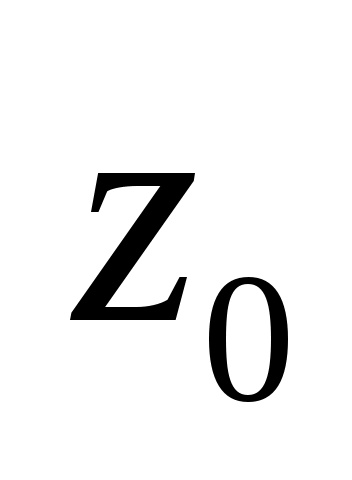 покладемо рівним покладемо рівним 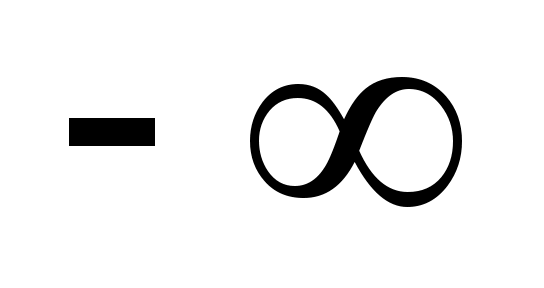 , а найбільше значення , а найбільше значення 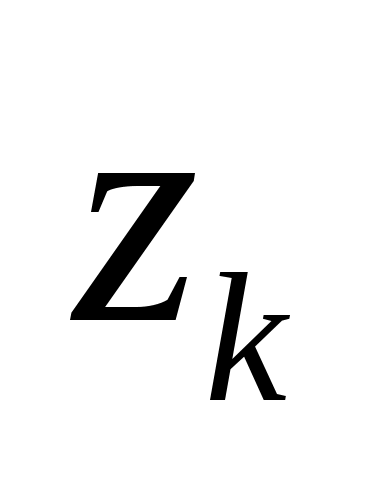 покладемо рівним покладемо рівним 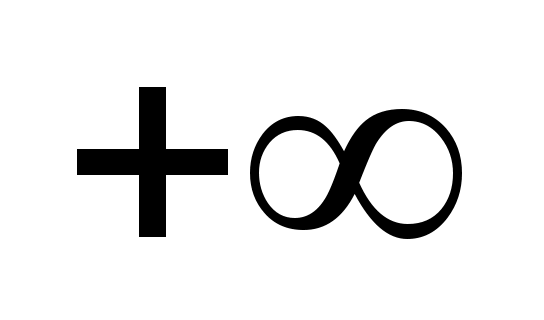 . .
Обчислимо теоретичні ймовірності 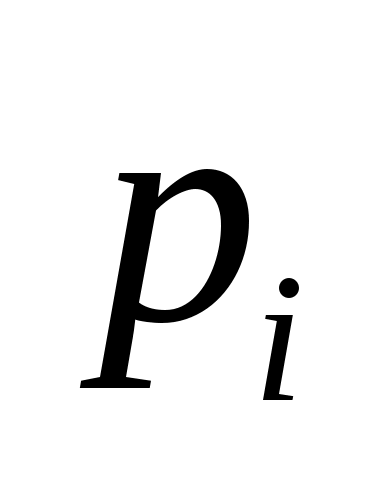 потрапляння випадкової величини потрапляння випадкової величини 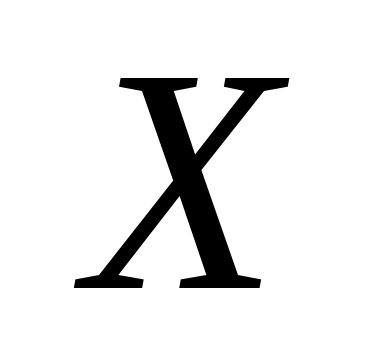 в інтервали в інтервали 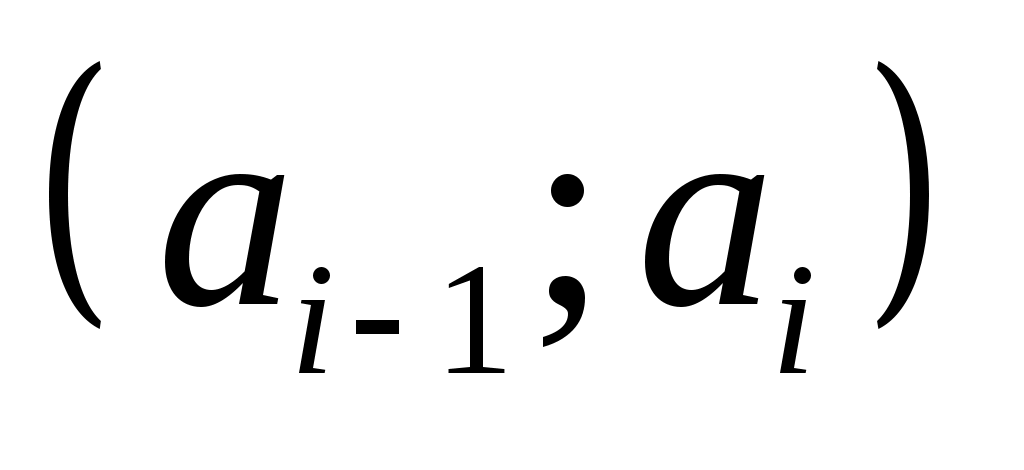 за формулою за формулою 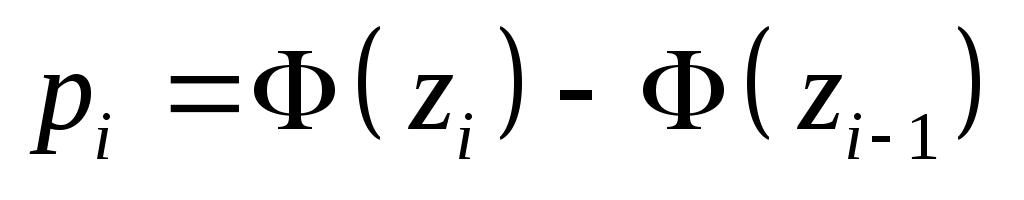 , де , де 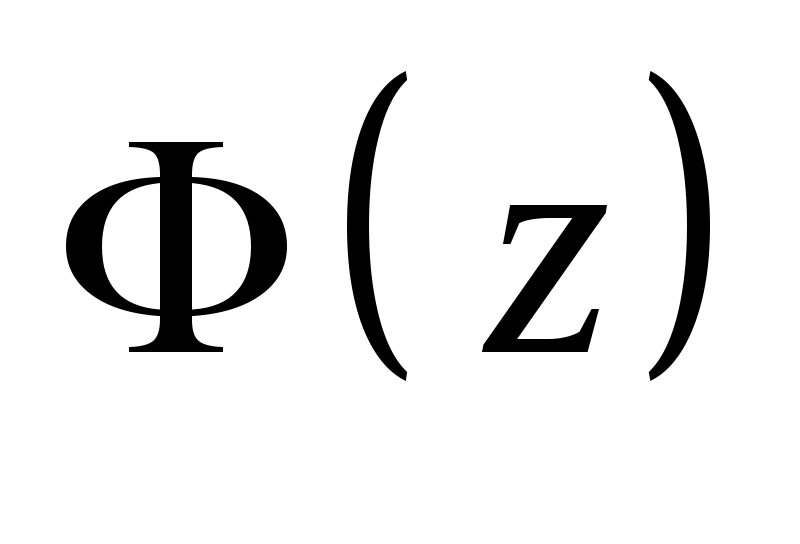 – функція Лапласа, та теоретичні частоти – функція Лапласа, та теоретичні частоти 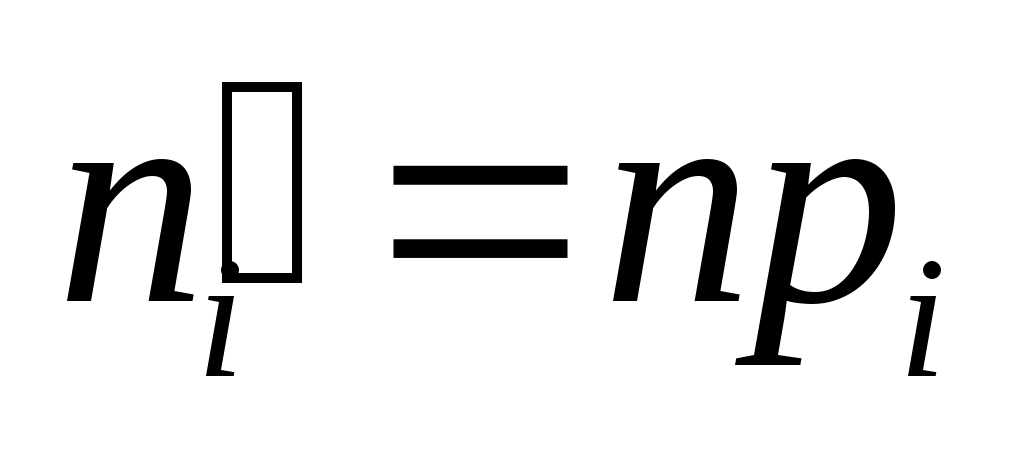 (тут (тут 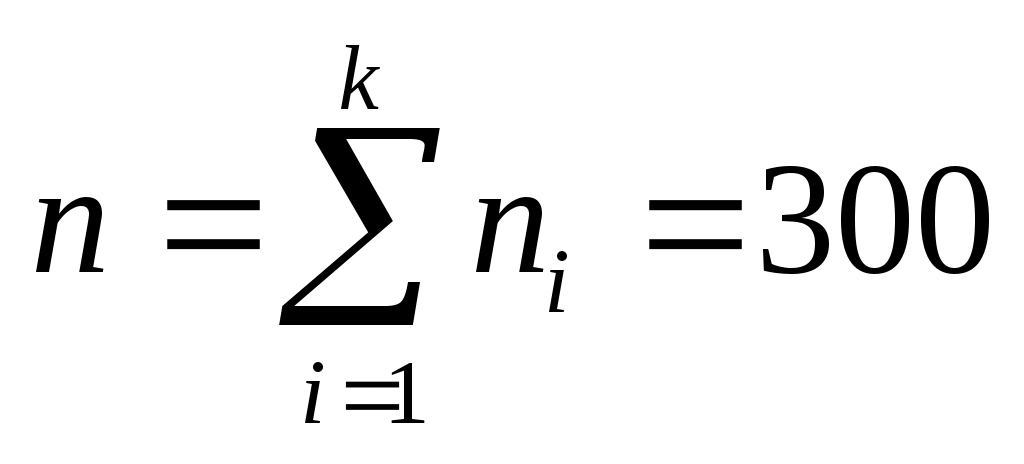 – об’єм вибірки). Для цього заповнимо розрахункову таблицю: – об’єм вибірки). Для цього заповнимо розрахункову таблицю:
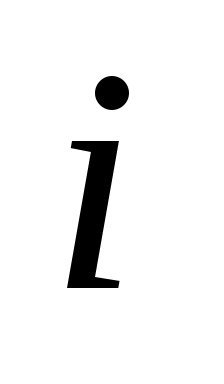
|
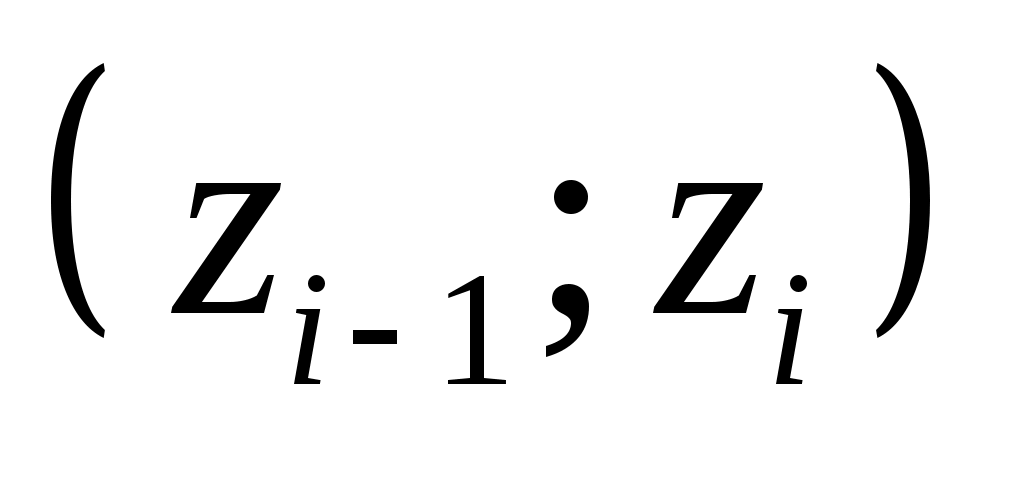
|
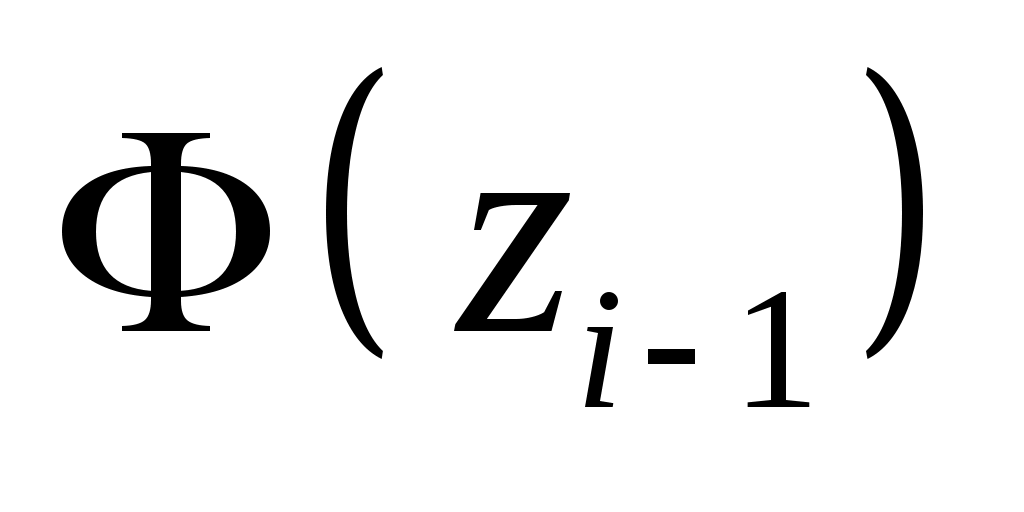
|
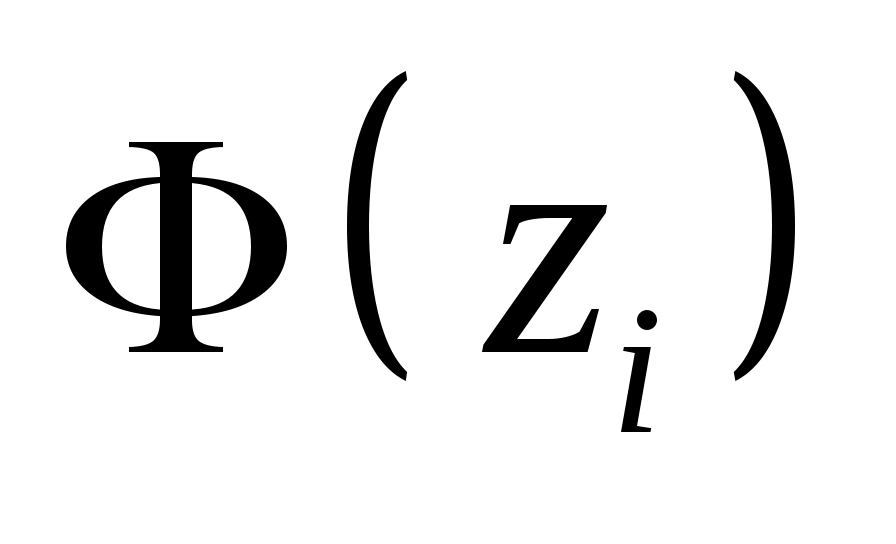
|
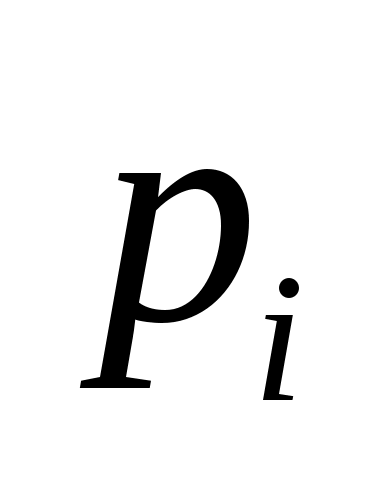
|
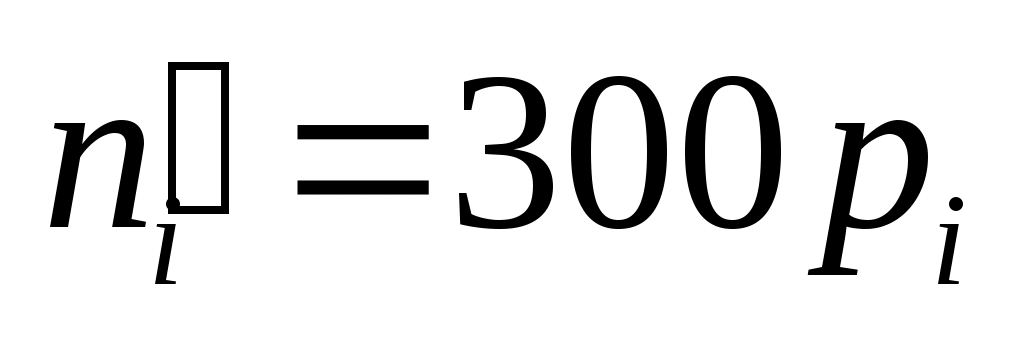
|
1
|
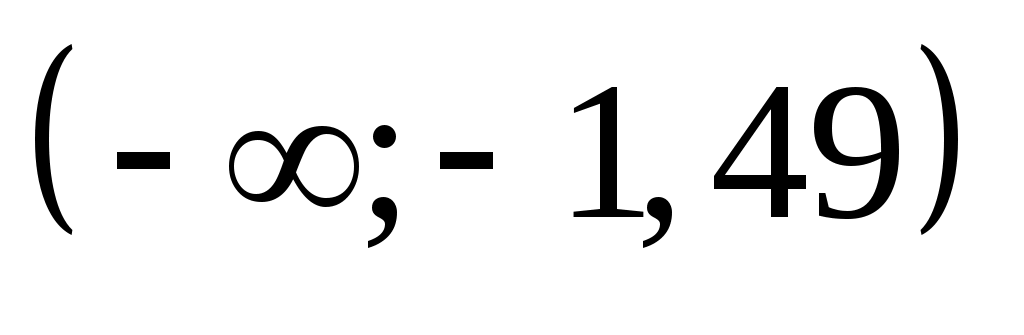
|
–0,5000
|
–0,4319
|
0,0681
|
20,43
|
2
|
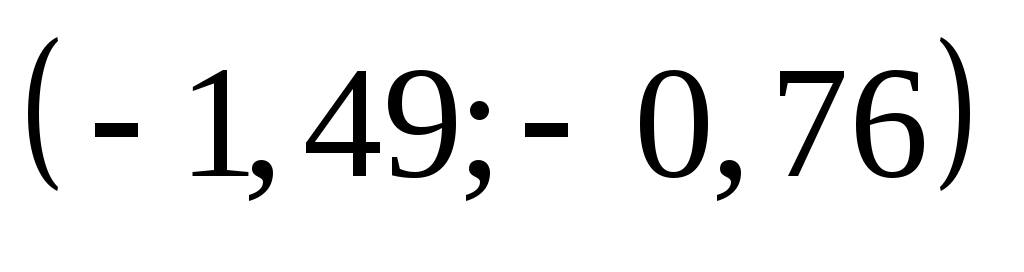
|
–0,4319
|
–0,2764
|
0,1555
|
46,65
|
3
|
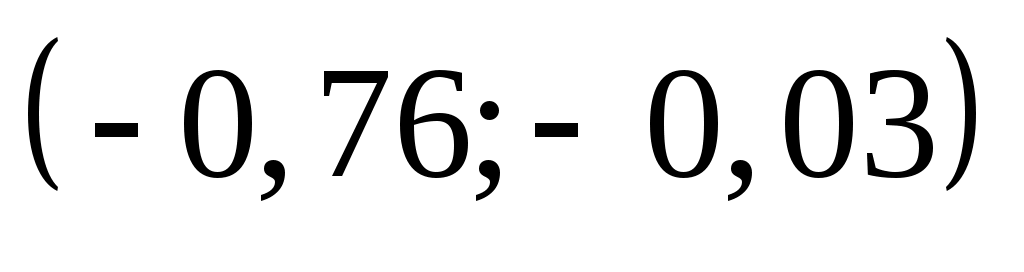
|
–0,2764
|
–0,0120
|
0,2644
|
79,32
|
4
|
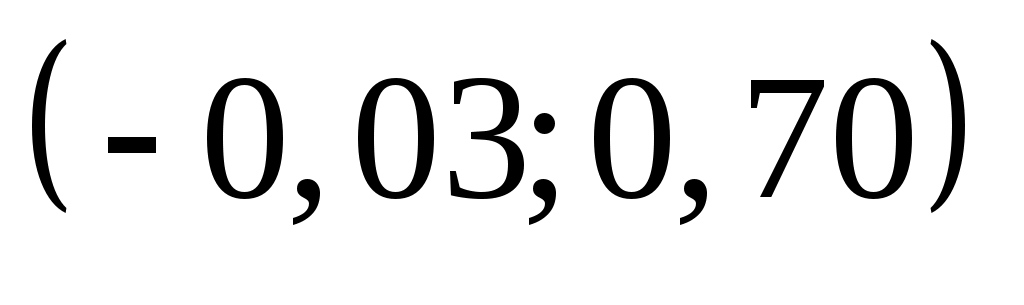
|
–0,0120
|
0,2580
|
0,2700
|
81,00
|
5
|
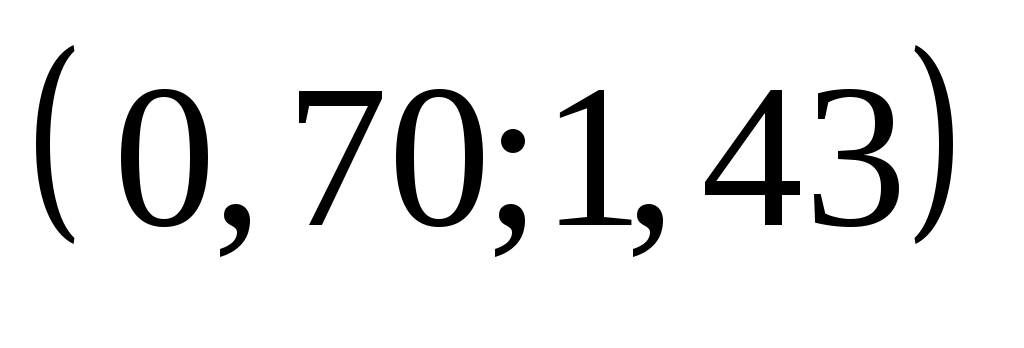
|
0,258
|
0,4236
|
0,1656
|
49,68
|
6
|
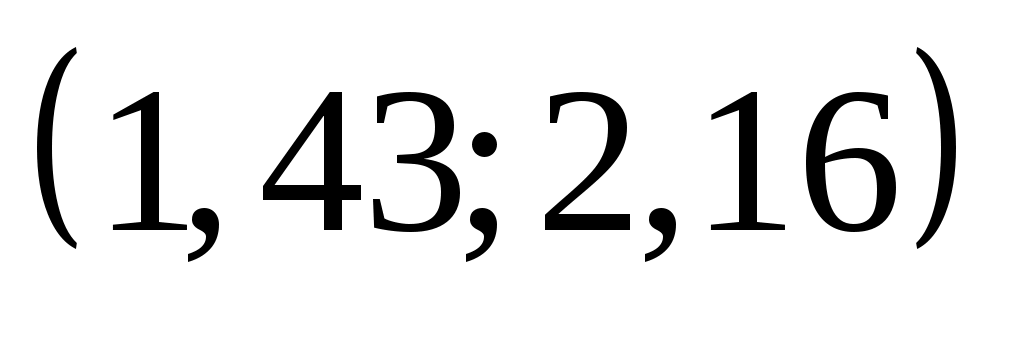
|
0,4236
|
0,4846
|
0,0610
|
18,30
|
7
|
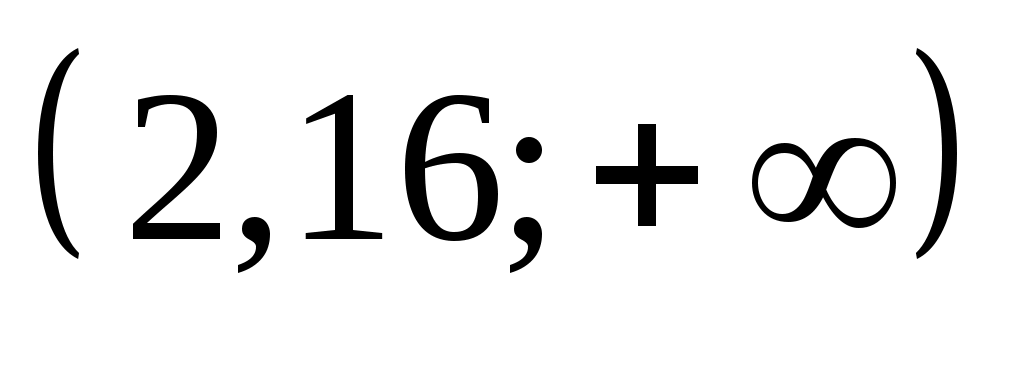
|
0,4846
|
0,5000
|
0,0154
|
4,62
|
|
|
|
|
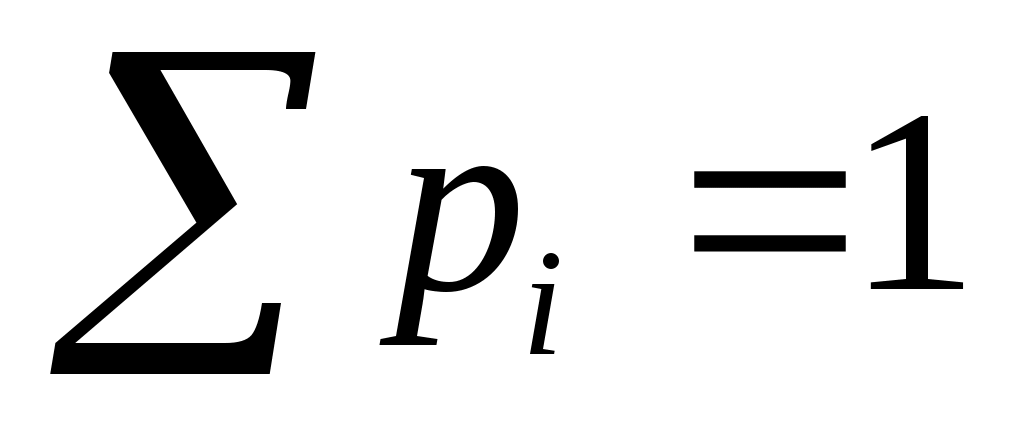
|
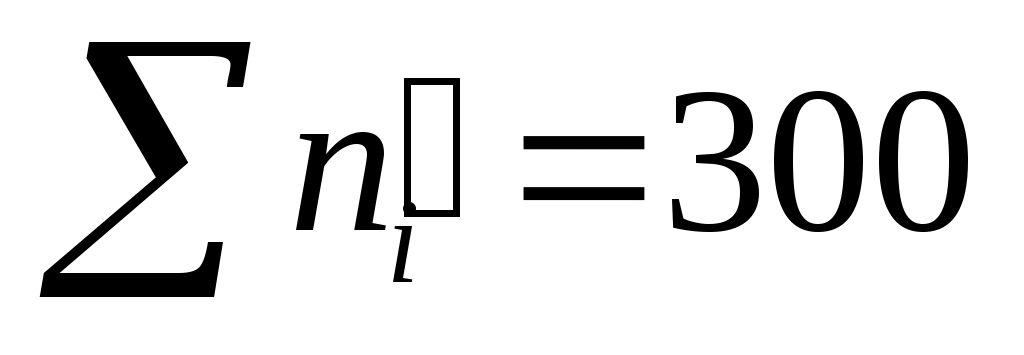
|
Обчислимо вибіркове значення критерію 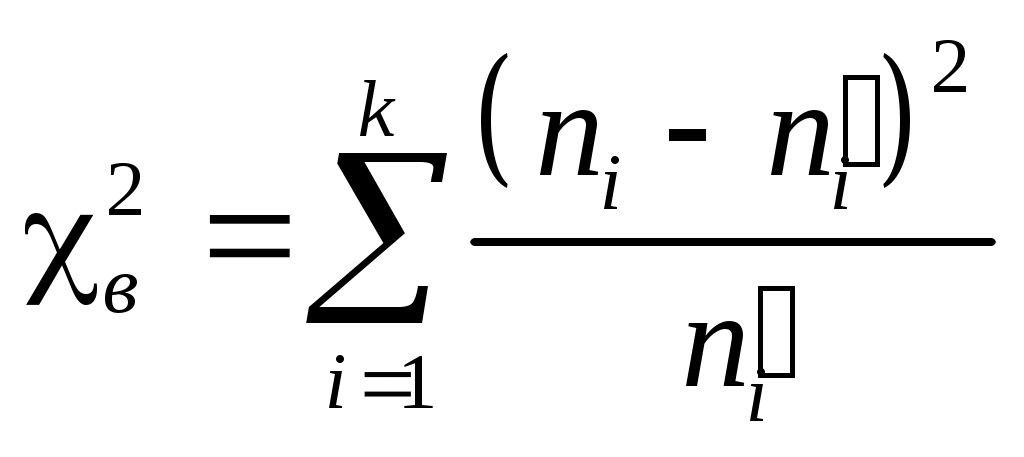 . Для цього заповнимо наступну розрахункову таблицю: . Для цього заповнимо наступну розрахункову таблицю:
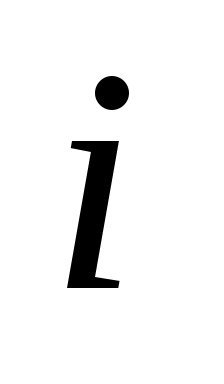
|

|
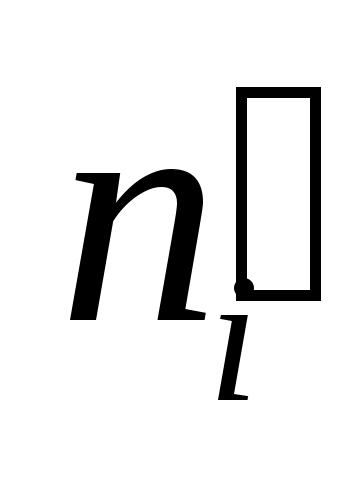
|
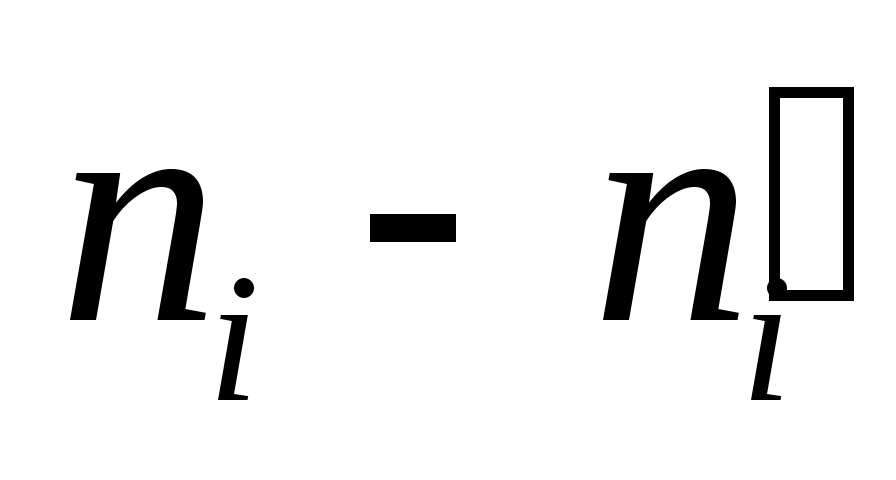
|
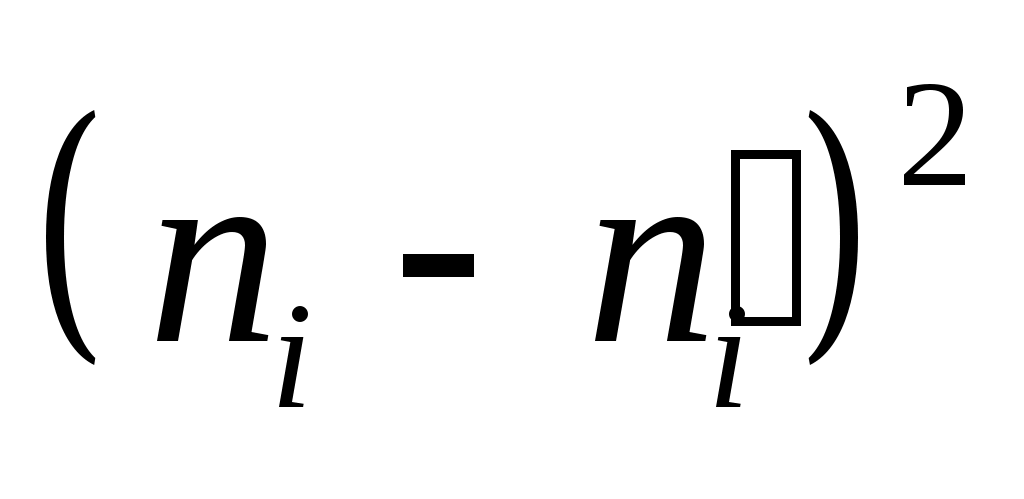
|
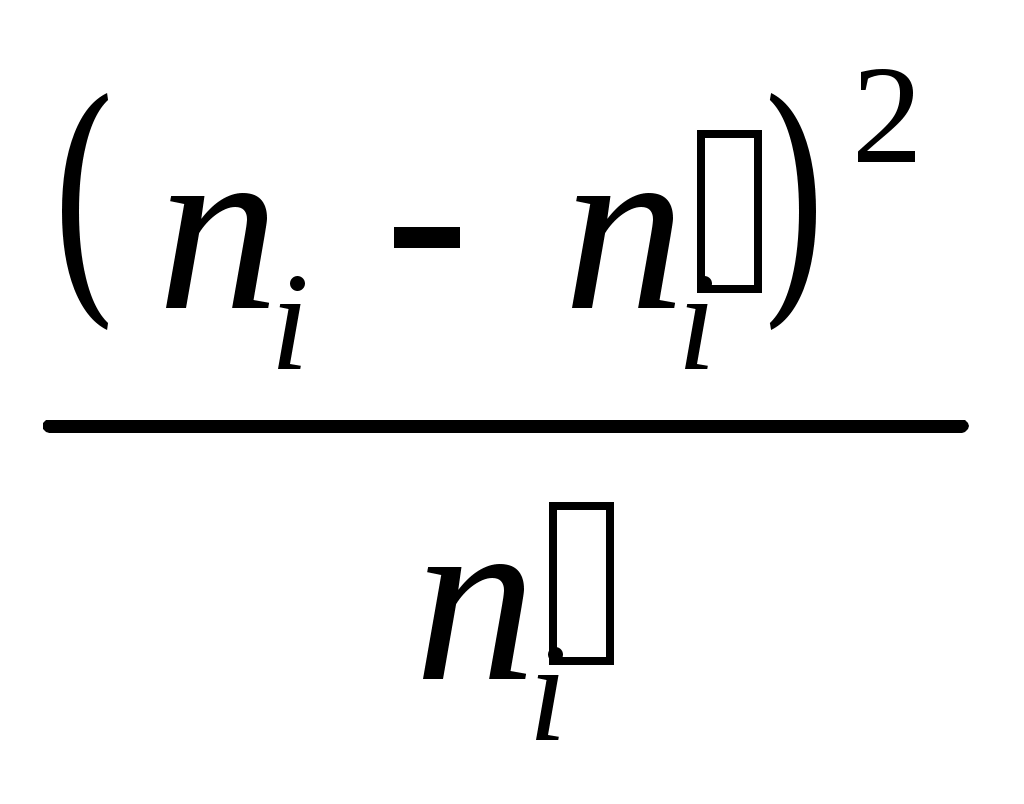
|
1
|
20
|
20,43
|
–0,43
|
0,1849
|
0,0091
|
2
|
47
|
46,65
|
0,35
|
0,1225
|
0,0026
|
3
|
80
|
79,32
|
0,68
|
0,4624
|
0,0058
|
4
|
89
|
81,00
|
8,00
|
64,0000
|
0,7901
|
5
|
40
|
49,68
|
–9,68
|
93,7024
|
1,8861
|
6
|
16
|
18,30
|
–2,30
|
5,2900
|
0,2891
|
7
|
8
|
4,62
|
3,38
|
11,4244
|
2,4728
|
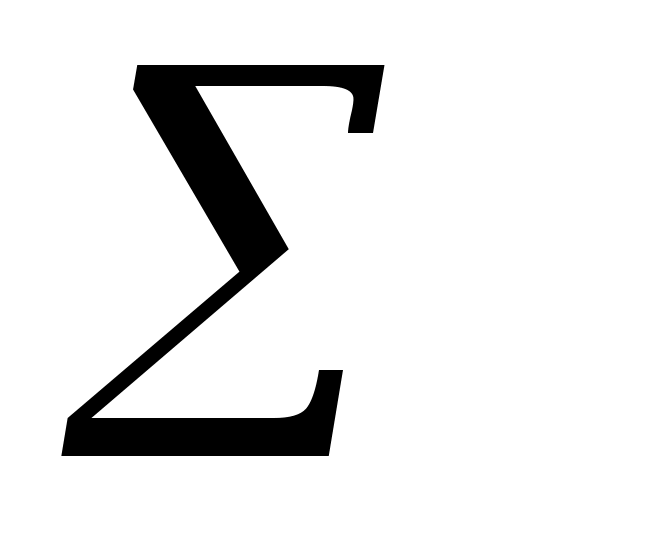
|
300
|
300
|
|
|
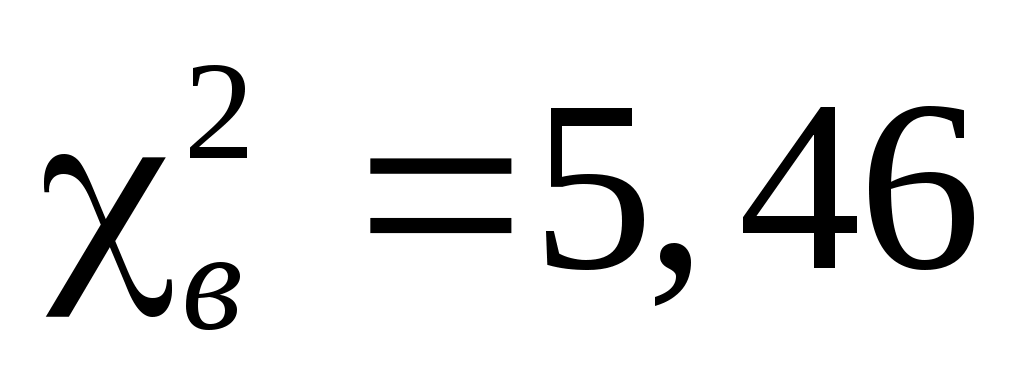
|
За таблицею критичних точок розподілу 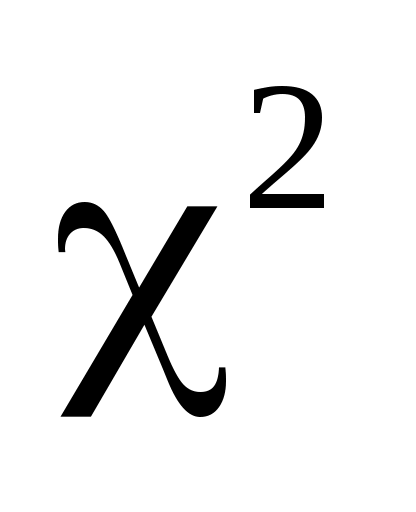 по рівню значущості по рівню значущості 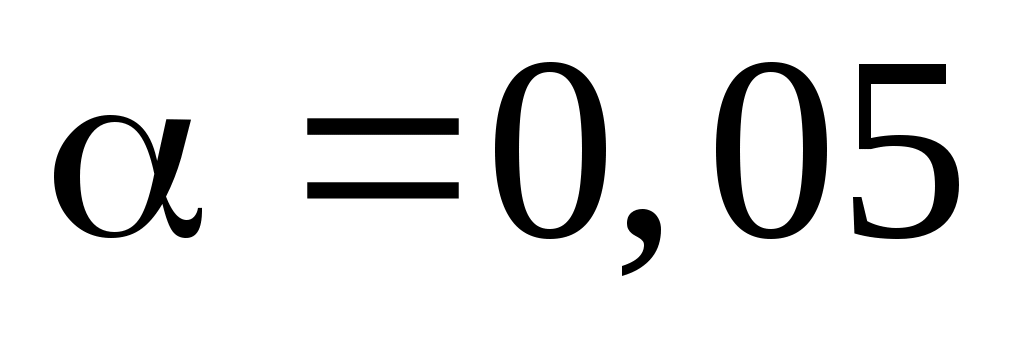 та числу ступенів свободи та числу ступенів свободи 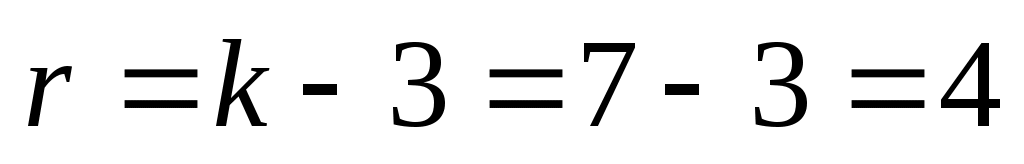 знаходимо критичну точку правосторонньої критичної області знаходимо критичну точку правосторонньої критичної області 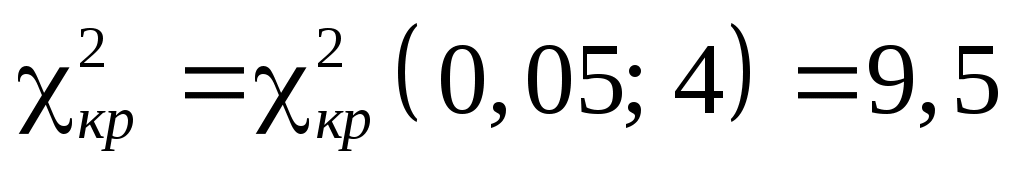 . .
Оскільки 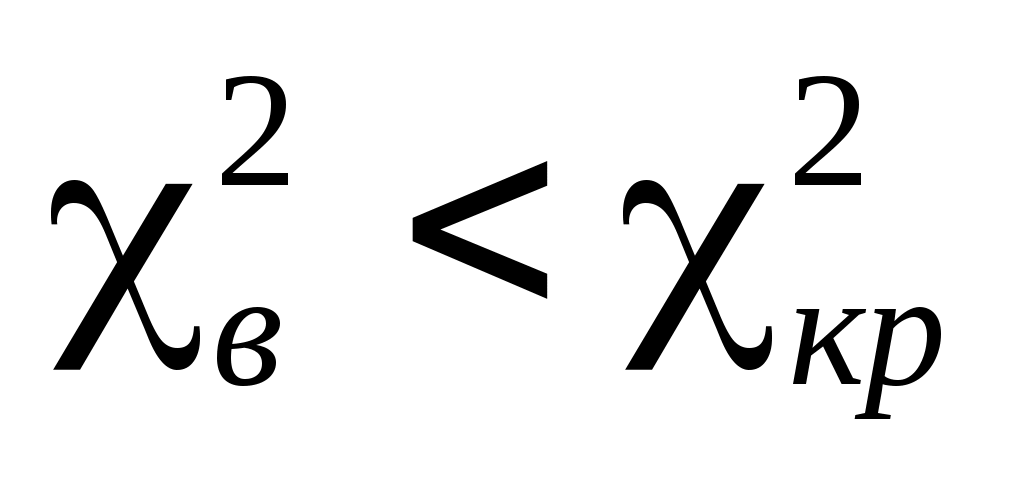 , то немає підстав відхилити нульову гіпотезу. Отже, статистичні дані узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності. , то немає підстав відхилити нульову гіпотезу. Отже, статистичні дані узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.
|
 Скачать 2.83 Mb.
Скачать 2.83 Mb.
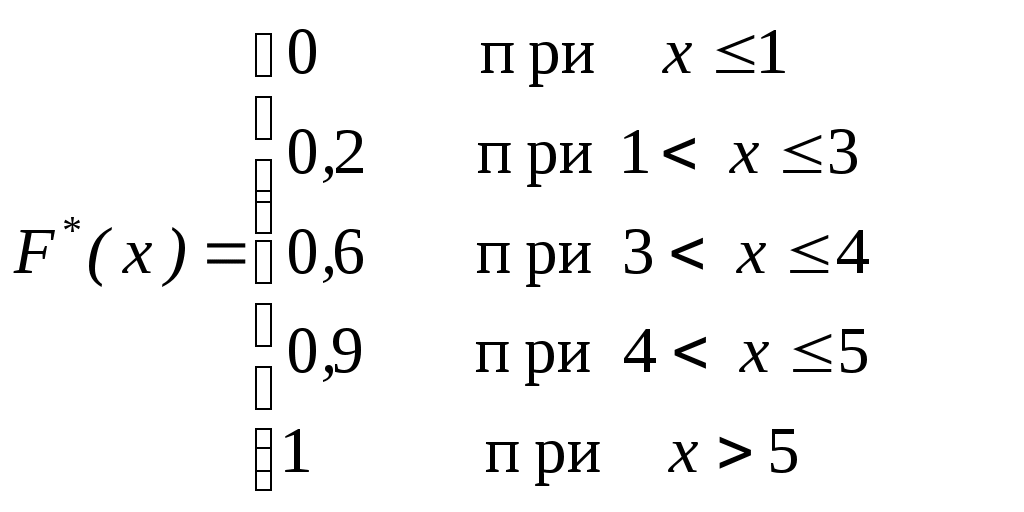 .
.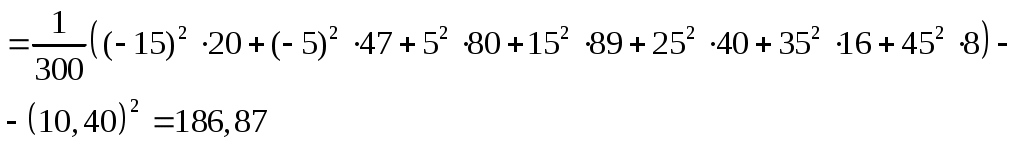 і вибіркове середнє квадратичне відхилення
і вибіркове середнє квадратичне відхилення 
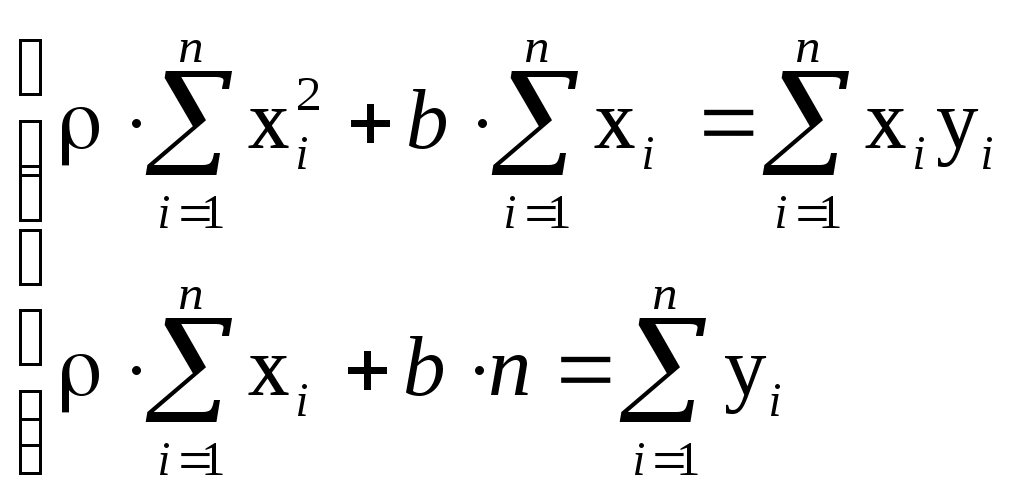 .
.