Методика изучения геометрического материала. Методика изучения геометрического материала

• Название: Методика изучения геометрического материала
• Дата: 01.12.2021
• Размер: 192 Kb.
• Имя файла: Методика изучения геометрического материала.doc
• Тип: Документы; #287664

МЕТОДИКА ИЗУЧЕНИЯ ГЕОМЕТРИЧЕСКОГО МАТЕРИАЛА

Основной задачей изучения геометрического материала в начальных классах является формирование у учащихся четких пред­ставлений и первичных понятий о таких плоских геометрических фигу­рах, как точка, прямая линия, отрезок прямой, ломаная линия, угол, многоугольник, круг. Также формируются представления о объемных телах таких, как куб, призма, пирамида, конус, цилиндр, шар.

При этом система упражнений и задач геометрического со­держания и методика работы над ними должны способствовать развитию пространственных представлений и умения оперировать ими у детей, умений на­блюдать, сравнивать, абстрагировать и обобщать.

Одной из задач обучения является выработка у учащихся практических умений измерения и построения геометрических фигур с помощью чертежных и измерительных инструментов и без них (измерить на глаз, начертить от руки и т.п.). Следует также дать первоначальные представления о точности построе­ний и измерений.

Учитывая задачи, намеченные программой, при изучении геометрического материала следует широко использовать раз­нообразные наглядные пособия. Это демонстрационные, обще­классные модели геометрических фигур, изготовленные из цвет­ного картона или плотной бумаги, плакаты с изображениями фигур, предметов различной формы, а также геометрических фигур, чертежи на доске, диафильмы. Кроме того, требуются ин­дивидуальные наглядные пособия — такой раздаточный матери­ал, как полоски бумаги, палочки различной длины, вырезанные из бумаги фигуры и части фигур. В качестве учебного пособия при изучении целого ряда геометрических объектов целесообразно использовать геоплан. При изучении отдельных тем полезно изготовить с детьми самодельные наглядные пособия: модель прямого угла, раздвижную модель угла (малку), па­летку, модели единиц измерения площади и др.

В классе необходимо иметь набор чертежно-измерительных инструментов для выполнения чертежей на доске: линейку, чер­тежный треугольник, циркуль. Аналогичные инструменты долж­ны быть и у каждого ученика. У незрячих и частичнозрячих школьников должны быть наборы брайлевских чертежно-измерительных инструментов, а также чертежные приборы Семевского, «Школьник».

Наиболее эффективными методами изучения геометрическо­го материала являются практические: моделирова­ние фигур из бумаги, из палочек, из проволоки, построение геометрических объектов на геоплане и преобразование их; черчение, изме­рение и др. При этом важно обеспечить разнообразие объектов, для того чтобы, варьируя несущественные признаки (цвет, размер, расположение на плоскости и др.), помочь детям выделить и усвоить существенные признаки — форму предметов, свойства фигур и т.п.

Там, где возможно, изучение геометрического материала на уроке должно связываться с изучением арифметического и алгебраического материала, хотя формирование геометрических представлений и понятий представляет самостоятельную и довольно специфическую линию работы.

Раскрывая геометрический материал младшим школьникам, надо учитывать, что первые представления о форме, размерах и взаимном положении предметов в пространстве дети накапливают еще в дошкольный период. В процессе игр и практической деятельности они манипулируют предметами, рассматривают, ощупывают их, рисуют, лепят, конструируют и постепенно вычленяют среди других свойств их форму. К 6–7 годам многие дошкольники правильно показывают предметы, имеющие форму шара, куба, круга, квадрата, треугольника, прямоугольника. Однако уровень обобщения этих понятий еще не высок: дети противопоставляют квадрат прямоугольнику, не узнают знакомую форму предмета, если сам предмет им не знаком. Ребенка приводят в замешательство непривычные соотношения сторон или углов фигур; иное, чем всегда, расположение на плоскости и даже очень большие или очень маленькие размеры фигур. Названия фигур дети часто смешивают или заменяют названиями предметов (так, треугольник дети называют «уголком», «крышей», «флажком» и т.п.)

Характеризуя положение предметов в пространстве, дошкольники более свободно устанавливают пространственные отношения, если «началом отсчета» является сам ребенок (слева — справа, впереди — позади, вверху — внизу, ближе — дальше и т.д. по отношению к нему). Гораздо труднее ребенок устанавливает положение предметов на плоскости или в пространстве по отношению к другому предмету или к другому человеку.

При обучении в школе необходимо опираться на имеющийся опыт детей, уточнять и обогащать их представления.
Точка, прямая и кривая линии, отрезок прямой

У учащихся I–IV классов надо формировать четкие образы точки, прямой и кривой линий, отрезка прямой. Задача учителя — научить вычленять, называть и правильно показывать эти фигуры, изображать их на бумаге и на доске, а начиная со II класса обозначать с помощью букв. Дети должны научиться измерять и чертить отрезки заданной длины.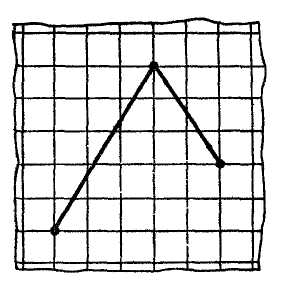

С точкой учащиеся знакомятся с первых шагов обучения в I классе. Готовясь к письму цифр, дети по образцу учителя выполняют такие задания: поставьте точку в середине клеточки (в левом нижнем углу клетки, в середине од­ной из сторон клетки и т.п.); соеди­ните поставленные точки по образцу (рис. 1).

После знакомства с прямой ли­нией дети учатся ставить точки на прямой, проводить прямые линии через 1, 2, 3 заданные точки, уста­навливать положение точки относи­тельно прямой линии (лежит на пря­мой, не лежит на прямой). После знакомства с отрезком прямой ана­логичные задания выполняются с точкой и отрезком, при этом дети убеждаются, что точка, лежа­щая на отрезке (т.е. между концами отрезка), делит его на два отрезка.

Когда происходит знакомство с элементами многоугольника, учащиеся узнают о том, что вершины многоугольников — это точки. Например, учитель предлагает детям поставить 3 точки так, как показано на доске (точки не лежат на одной прямой), соединить их отрезками и сказать, какая фигура получилась; за­тем сосчитать, сколько у нее вершин.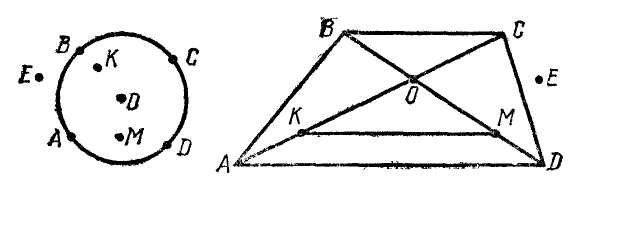

Во II классе учащиеся знакомятся с обозначением точек ла­тинскими буквами. Учитель поясняет, что для различения точек на чертеже принято обозначать их заглавными латинскими бук­вами, например: D, К, М, О, А, Е и т.д., которые пишутся око­ло точки (показывается образец на доске). Дети упражняются в обозначении точек буквами и чтении обозначенных буквами точек. С этого времени наряду с устными упражнениями можно включать и письменные, что гораздо эффективнее, так как за­ставляет работать каждого ребенка. Например, по чертежу, данному на доске, предлагают выписать в первую строчку те точки, которые лежат внутри круга (четырехугольника), во вто­рую строчку — точки, которые лежат вне круга (четырехуголь­ника), в третью строчку — точки, которые лежат на границе круга (четырехугольника) (рис. 2).

Формирование у первоклассников представления о прямой линии происходит в процессе выполнения ими разнообразных практических упражнений. При этом прямую линию сопостав­ляют с кривой. Например, натягивают нить (шнур, шпагат), за­тем ослабляют нить так, чтобы она провисала; рассматривают рисунки, на которых изображена, положим, прямая дорога и извилистая тропинка, разрезают лист бумаги по линии, полу­ченной перегибанием листа, и т.п. Каждый раз выясняют, какая получилась линия — прямая или кривая.

Дети должны научиться узнавать прямую линию, начерчен­ную в любом положении на плоскости, отличать ее от кривой, уметь проводить прямые, используя линейку. С целью выработ­ки этих умений учащиеся чертят в тетрадях прямые и кривые линии, находят и показывают их на окружающих предметах, а также среди линий, начерченных на доске.

В процессе выполнения упражнений дети знакомятся с не­которыми свойствами прямой. Например, упражняясь в прове­дении линий через точки, дети обобщают свои наблюдения: че­рез одну точку можно провести сколько угодно прямых или кри­вых линий; через две точки можно провести только одну пря­мую, а кривых сколько угодно.

С отрезком прямой учащиеся знакомятся также практи­чески: отмечают на прямой две точки, и учитель поясняет, что эту часть прямой от одной точки до другой называют отрезком прямой, или кратко — отрезком, а точки — концами отрезка. Дети ставят точки на других прямых, начерченных на доске, и показывают полученные отрезки и концы отрезков. Затем учи­тель показывает, как изображается на чертеже отрезок (концы отрезка отмечает точками или штрихами), сравнивает с изо­бражением прямой. Учащиеся показывают на чертежах и сами чертят прямые и отрезки прямых и постепенно осознают, что отрезок ограничен, а прямая не ограничена, мы изображаем на бумаге только часть прямой. Закреплению понятия об отрезке способствуют такие упражнения: показать отрезки прямой на окружающих предметах; соединить отрезком две точки; про­вести отрезок через три точки, лежащие на одной прямой; по­казать все получившиеся при этом отрезки. До измерения отрезков вводится понятие о равных, и неравных отрезках, разъяс­няется способ установления этих отношений (наложением). В дальнейшем после с сантиметром, дециметром, метром и т.д. учащиеся выполняют большое количество упражнений в измерении и черчении отрезков, решают задачи с отрезками (на увеличение и уменьшение на несколько единиц и в несколько раз, на разностное и кратное сравнение). Посте­пенно учащиеся убеждаются, что равные отрезки содержат оди­наковое число выбранных единиц длины, а неравные — неоди­наковое число: в том отрезке содержится больше единиц, кото­рый длиннее. Таким образом, становится возможным судить о равенстве и неравенстве отрезков на основе сравнения чисел, выражающих длину этих отрезков.

Выделяя элементы многоугольников, учащиеся устанавли­вают, что стороны многоугольников — отрезки. Упражнения на выделение отрезков необходимо усложнять постепенно, чтобы они были посильны учащимся. Так, чтобы дети смогли увидеть и показать все отрезки на таких чертежах, как третий (рис. 3), надо научить их выполнять более легкие задания — называть и показывать отрезки на чертежах, подобных первому и второму (см. тот же рисунок).

К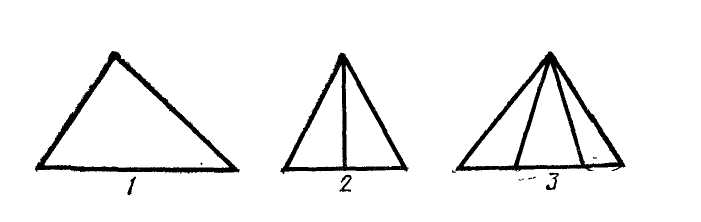
огда учащиеся ознакомятся во II классе с обозначением отрезков буквами, даются письменные упражнения, которые за­крепляют умения выделять отрезки, являющиеся частями дру­гих отрезков, а также отрезки, составленные из других отрез­ков. Например, предлагают записать все отрезки, которые име­ются на чертеже (рис. 4), записать отрезки с началом в точ­ке О (рис. 5), измерить с помощью линейки и выписать равные отрезки (рис. 6).

Постепенно учащиеся осознают, что отрезок может быть об­щей стороной нескольких многоугольников, и, опираясь на это, во II–III классах выполняют упражнения на построение отрез­ков внутри многоугольников, так чтобы при этом образовыва­лись новые фигуры; например, провести внутри пятиугольника один отрезок так, чтобы при разрезании получились треуголь­ник и четырехугольник или два четырехугольника, или тре­угольник и шестиугольник (рис. 7). Учащиеся выполняют зада­ние в тетрадях, а затем выявляются и показываются на доске различные решения каждой задачи.
Т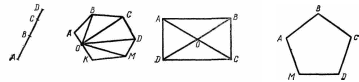
акие упражнения развивают у де­тей воображение и пространственные представления, а также закрепляют геометрические понятия.
Многоугольник, угол, круг

Понятия об этих фигурах формируются у детей постепенно в течение всего начального обучения и в последующих классах. Первоначально, при изучении пер­вого десятка, геометрические фигуры используются как дидактический материал. Опираясь на него, дети учатся считать, решать задачи, вычислять, составлять орна­менты, сравнивать, классифицировать и др. Попутно уточняются представления отдельных фигур, запоминаются их названия: круг, треугольник, квадрат.

Далее приступают к изучению отдельных видов многоуголь­ников. На этом этапе вычленяют элементы многоугольников; стороны, углы, вершины. Так, при изучении числа 3 рассматри­вают различные треугольники. На моделях треугольников, из­готовленных из цветной плотной бумаги, пластмассы, дерева и т.п., учащиеся показывают три стороны, три угла и три вер­шины в каждой фигуре. Затем дети сами моделируют треуголь­ники из палочек и кусочков пластилина или из полосок бумаги; обозначив точками вершины, чертят и раскрашивают треуголь­ники в тетрадях; находят предметы, имеющие форму треуголь­ников; отыскивают треугольники среди других геометрических фигур, начерченных на доске или выставленных на наборном полотне в виде моделей из плотной цветной бумаги. При этом учитель должен позаботиться, чтобы учащиеся рассматривали различные виды треугольников (равносторонние и разносторон­ние, прямоугольные, тупоугольные и остроугольные). Это помо­жет формированию правильного представления о треугольнике. В процессе указанных упражнений дети учатся правильно показывать элементы треугольника: вершины (показывают точки), стороны (показывают отрезки, проводя указкой от од­ного конца отрезка до другого), углы (показывают угол вместе с его внутренней областью веерообразным движением указки от одной стороны угла до другой, поместив один конец ее в верши­ну угла).

Далее в таком же плане рассматривают четырехугольники, пятиугольники и т.д., приурочивая эту работу к изучению со­ответствующих чисел в пределах первого десятка. Выделяя эле­менты многоугольников, учащиеся подмечают связь между чис­лом элементов и названием фигуры (три стороны, три верши­ны, три угла — треугольник; четыре стороны, четыре вершины, четыре угла— четырехугольник и т.д.). Кроме того, дети осозна­ют, что у многоугольника одинаковое число углов, вершин и сторон. Все эти сведения дети усваивают практически при выполне­нии упражнений с готовы­ми моделями, при вырезы­вании, черчении и моделировании многоугольников. Для модели­рования лучше использовать набор палочек или бумажных по­лосок различной длины, чтобы наблюдения не ограничива­лись равносторонними многоугольниками. Кроме того, дети будут сталкиваться с такими случаями, когда не из любых 3 (4,5 и т.д.) палочек оказывается возможным построить соответствующий многоугольник.

Понятие многоугольника можно ввести как обобщение рас­смотренных видов многоугольников.

В процессе работы над многоугольниками учащиеся получа­ют первые сведения об углах (угол образуют две стороны многоугольника, выходящие из одной его вершины), учатся по­казывать углы многоугольника.

Д 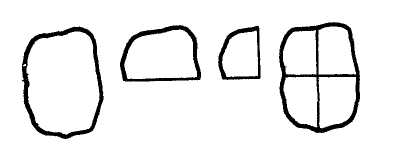алее второклассники знакомятся с прямым углом. Это можно провести так. Дети под руководством учителя изготовля­ют модель прямого угла: они дважды перегибают пополам лист бумаги произвольной формы и устанавливают, что получившие­ся при этом две пересекающиеся прямые линии образуют четы­ре одинаковых угла. Учитель сообщает, что такие углы называ­ют прямыми (рис. 8). 3aтeм дети наложением устанавливают, что, несмотря на различные листы бумаги, все получившиеся прямые углы равны. Пользуясь моделью прямого угла, учащие­ся находят прямые и непрямые углы на окружающих предме­тах, в частности на чертежном треугольнике. В дальнейшем для установления вида угла используют прямой угол чертежного треугольника (лучше из прозрачной пластмассы): если углы сов­падают (т.е. совмещаются их стороны и вершины), то данный угол прямой, если не совпадают — не прямой. Для закрепления представления прямого угла включают специальные упражнения.

Н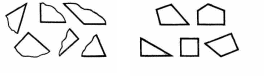
апример, среди разнообразных данных углов предлагают найти прямые углы (рис. 9); в данных многоугольниках най­ти прямые углы (рис. 10); начертить пря­мой угол в тетради, используя ее разли­новку; начертить треугольник (четырех­угольник), имеющий прямой угол, и др.

Ч 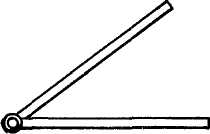тобы у детей сформировалось пред­ставление угла вместе с его внутренней областью, на первых порах работают с бу­мажными моделями углов. Но в дальнейшем наряду с бумажны­ми моделями используют модель «раздвижного угла» (малку). Рекомендуется изготовить каждому ученику такую модель угла из двух палочек, скрепленных кусочком пластилина или гвозди­ком (рис. 11). С помощью такой модели дети наглядно убежда­ются, что величина угла зависит не от длины его сторон, а от взаимного положения сторон относительно друг друга: чем ближе стороны сдвинуты, тем угол меньше, чем дальше раздвинуты — тем угол больше (рассматриваются пока углы меньше развер­нутого).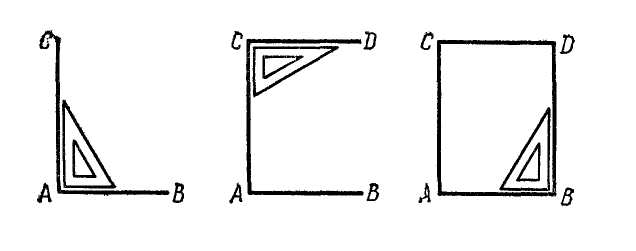

Понятие угла закрепляется у учащихся в дальнейшем в про­цессе изучения многоугольников, например при рассмотрении прямоугольника. Среди нескольких четырехугольников первоклассники с помощью модели прямого угла находят че­тырехугольники с одним-двумя прямыми углами, а также четы­рехугольники, у которых все углы прямые (рис. 12). Учитель сообщает, что в последнем случае четырехугольники называют прямо­угольниками. Учащиеся находят в окружающей их обстановке предметы прямоугольной формы, показывают прямоугольники среди других геометрических фигур (рис. 13), начерченных на доске или выставленных на наборном полотне, вырезают их из бумаги в клеточку, чертят по точкам в тетрадях и т.п. В процессе таких упражнений у детей формируется наглядный образ прямоуголь­ника, запоминается его название.

Н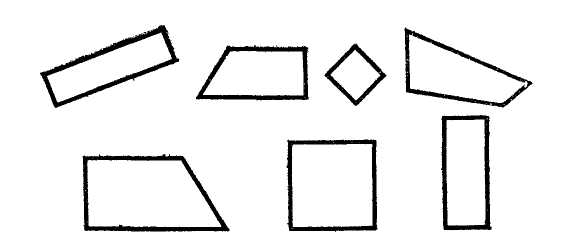
а следующем этапе работы учащиеся второго класса знакомятся с одним из свойств прямоугольника: противоположные стороны прямоугольника равны между собой. Уточнив сначала, понима­ют ли дети, какие стороны прямоугольника можно назвать про­тивоположными, учитель предлагает учащимся на бумажных моделях прямоугольника непосредственным наложением срав­нить противоположные стороны. Измеряя противоположные сто­роны прямоугольников, данных в учебнике и на доске, дети также подтверждают и обобщают свои наблюдения. Знание это­го свойства сторон прямоугольника закрепляется в дальнейшем, когда учащиеся чертят прямоугольники по двум заданным его сторонам (длине и ширине). В II–III классах учащиеся выполняют построение прямоугольников с помощью линейки (чертят прямые углы, пользуясь разлиновкой тетрадей), а в IV классе при по­строении прямоугольника используют линейку и чертежный тре­угольник.

После того как учащиеся второго класса усвоят свойство противо­положных сторон прямоугольника, из множества прямоугольни­ков вычленяют квадраты — прямоугольники с равными сторо­нами.

Работа на уроке так и организуется, чтобы учащиеся увиде­ли, что квадрат — это частный случай прямоугольника. Детям предлагается, например, измерить стороны у нескольких прямо­угольников, начерченных на доске или вырезанных из бумаги. Среди них обнаруживаются такие прямоугольники, у каждого из которых стороны равны между собой. Дети сами вспоминают их название — квадраты. Чтобы подчеркнуть, что квадраты — это прямоугольники с равными сторонами, включают такие уп­ражнения: «Покажите прямоугольники, которые нельзя назвать квадратами; найдите среди данных четырехугольников четыре прямоугольника; найдите среди указанных прямоугольников два квадрата (рис. 13) и т.п.». В подобных упражнениях дети должны обосновывать свои суждения, проверяя с помощью чертежного треугольника, являются ли все углы четырехуголь­ника прямыми, а также устанавливая с помощью линейки, ка­ково в нем соотношение сторон.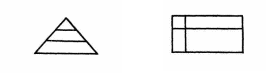




Большое значение для закрепления представлений о много­угольниках, а также для развития пространственных представ­лений в целом имеют задачи с геометрическим содержанием, которые включаются систематически начиная с I класса. Это задачи на деление заданных фигур так, чтобы получившиеся части имели указанную форму; задачи на со­ставление новых фигур из данных многоугольников (т.е. конструирование целого из частей), а также задачи на рас­познавание (вычленение) всевозможных геометрических фи­гур на заданном чертеже. Все эти задачи взаимосвязаны друг с другом. Решение задач каждого вида помогает при решении задач других видов. Поэтому они включаются, перемежаясь в определенной системе, так что число частей фигуры (из которых она составляется или на которые расчленяется) увеличивается постепенно. Например, разрежьте квадрат так, чтобы получи­лось два прямоугольника (два треугольника), а потом 4 тре­угольника, четыре квадрата и т.п.; из двух (а затем из четырех) треугольников (полученных, например, при разрезании квадрата по его диагоналям) сложите треугольник, четырехугольник и т. п , при этом вначале дают образец тех фигур, которые должны получиться при составлении (или при разрезании), а потом уже задание выполняется без образца. При вычленении знакомых фигур на чертеже сначала указывают, сколько и ка­ких фигур надо показать: найдите на чертеже 3 треугольника и 3 четырехугольника (рис. 14), а потом задание усложняется, на­пример: сосчитайте, сколько всего прямоугольников изображено на чертеже (рис. 15), или так: какие знакомые фигуры вы види­те на чертеже и сколько их. При выполнении таких упражнений по учебнику можно дать задания по вариантам, а затем предло­жить проверить учащимся друг друга. После этого вызванные учащиеся показывают фигуры по чертежу на доске, а осталь­ные проверяют правильность выполнения.

Начиная со II класса, когда учащиеся ознакомятся с обозна­чениями фигур буквами, подобные упражнения выполняются с записью решений и необходимых построений в тетрадях

Для закрепления представлений о многоугольниках и развития пространственных представлений в целом используется следующая система типичных геометрических задач:

1. 
   Задачи на распознавание, вычленение фигур заданного вида на чертеже;
   
2. 
   Задачи на деление геометрической фигуры на несколько фигур заданного вида;
   
3. 
   Задачи на составление новых фигур из данных многоугольников.
   

Все виды задач взаимосвязаны. Задачи двух последних видов представляют действия по образцу, по представлению, в практическом плане, в плане умственных действий.

Во IV классе учащиеся знакомятся с окружностью, учат­ся чертить окружности с помощью циркуля, знакомятся с эле­ментами окружности и круга — центром и радиусом. Все эти сведения усваиваются детьми в процессе практических упраж­нений. Например, соединив точки, лежащие на окружности, с центром и сравнив полученные отрезки, дети убеждаются в ра­венстве этих отрезков. Вводится название таких отрезков — ра­диус круга или окружности.

Сопоставив круг с многоугольником, учащиеся устанавли­вают, что границей многоугольника является замкнутая ломаная линия, а границей круга — замкнутая кривая линия — ок­ружность.

Чтобы учащиеся не смешивали круг и окружность, дают спе­циальные упражнения, например: проведите окружность и рас­красьте круг, отметьте центр круга или окружности, а также точки, лежащие внутри круга, вне круга, на окружности.

Затем в процессе упражнений у детей формируются умения чертить окружности указанного радиуса, а также делить с по­мощью циркуля окружность на 6, 3, 12 равных частей, делить перегибанием круг на 2, 4, 8, 3, 6 равных частей.
Ломаная линия, длина ломаной линии, периметр многоугольника

Опираясь на понятие отрезка, учащихся II класса знакомят с ломаной линией. Для этого по образцу, данному учите­лем, предлагают учащимся построить линию из палочек или бумажных полосок. Учитель дает название новой линии. Можно изготовить также модель ломаной, «сломав» на глазах у детей на части тонкую лучинку или кусок проволоки. На доске изо­бражают иногда ломаную с помощью цветной нити, натянутой между несколькими гвоздиками — «точками», не лежащими на одной прямой. Учащиеся чертят ломаные линии на доске и в тетрадях: ставят 3 (4, 5 и т.д.) точки, не лежащие на одной прямой, и соединяют их отрезками. Каждый раз дети подсчи­тывают, сколько отрезков содержит ломаная линия или сколько у нее звеньев. Так же с опорой на практические работы вводят понятия незамкнутой и замкнутой ломаной линии. Уча­щиеся строят из палочек (полосок бумаги, кусочков проволоки) ломаную линию, находят ее начало (начало первого отрезка) и конец (конец последнего отрезка). Учитель дает название такой ломаной — незамкнутая, а затем предлагает по образцу соеди­нить начало и конец незамкнутой ломаной линии. Учащиеся сами догадываются, что такая ломаная линия называется замк­нутой. При этом звенья соединяют так, чтобы они, кроме вер­шин, не имели общих точек.

В процессе упражнений устанавливают связь между замк­нутой ломаной линией и многоугольником, для которого лома­ная линия является границей: замкнутая ломаная линия из трех звеньев ограничивает треугольник, из четырех звеньев — четырехугольник и т.д.

Затем учащихся знакомят с измерением ломаных линий та­ким способом: измерить звенья ломаной и сложить полученные числа. Чтобы дети усвоили понятие длины ломаной линии, необ­ходимо включить достаточное количество упражнений в нахож­дении длины незамкнутых и замкнутых ломаных линий, кото­рые содержат различное число звеньев.

Понятие о периметре многоугольника дается в про­цессе решения конкретной задачи на нахождение длины замк­нутой ломаной линии. Учитель поясняет, что сумма длин сторон многоугольника называется его периметром. Можно на этом же уроке дать обозначение периметра буквой (Р = 24 см). Сначала лучше включать задачи на нахождение периметра многоуголь­ника с неравными сторонами, в процессе решения которых за­крепляется понятие о длине ломаной линии. Например, учащим­ся раздаются вырезанные из бумаги многоугольники или начер­ченные на карточках треугольники, четырехугольники и т.п. и дается задание найти периметр данных фигур. Можно предло­жить построить многоугольники по точкам, не лежащим на од­ной прямой, соединить их последовательно отрезками, обозна­чить и раскрасить полученный многоугольник, а потом измерить стороны и вычислить его периметр.

Затем специально рассматривается нахождение периметра равносторонних многоугольников, а также нахождение перимет­ра прямоугольника. Периметр этих фигур дети находят сначала путем измерения их сторон и сложения полученных чисел. Но тут же обращается внимание на свойства этих фигур — равен­ство всех сторон или равенство противоположных сторон. Уча­щиеся делают вывод о возможности сократить измерения: при нахождении периметра равностороннего треугольника, квадра­та и других многоугольников с равными сторонами достаточно измерить одну сторону, а затем умножить ее длину на число сторон многоугольника. При нахождении периметра прямо­угольника достаточно узнать его длину и ширину (т.е. основа­ние и высоту), затем умножить каждое из этих чисел на 2 и полученные произведения сложить. Здесь учащиеся, кроме гео­метрических, закрепляют также и арифметические знания. Опи­раясь на чертеж, они подмечают, что можно поступить и по-дру­гому: найти сумму длин смежных сторон, а затем умножить эту сумму на 2. Сравнивая полученные записи, например: Р = 4 • 2 + 6 • 2 и P = (4 + 6) • 2, дети устанавливают, что во втором случае умножали сумму на число, а в первом — каждое слагаемое умножали на это число и результаты складывали. Так как использованное свойство умножения суммы на число известно детям, То они убеждаются в правильности своих рас­суждений при нахождении периметра прямоугольника.

В дальнейшем во II–IV классах систематически решают задачи на вычисление периметра, а также задачи, им обратные. Например:

1. 
   Чему равна сторона квадрата, периметр которого равен 2 дм 4 см? Начертите такой квадрат.
   
2. 
   Участок квадратной формы с трех сторон обнесен забором, а одной стороной примыкает к дому, длина которого 9 м. Какова длина забора?
   
3. 
   В треугольнике одна из сторон равна 10 см, а две дру­гие равны между собой. Периметр треугольника 24 см. Какова длина каждой стороны треугольника?
   

При решении таких задач полезно выполнять чертежи (хотя бы схематические). Наряду с решением готовых задач рекомен­дуется предлагать учащимся задания на составление подобных задач с геометрическим содержанием (подобрать и вставить в условие пропущенные числовые значения; составить задачу, об­ратную решенной; составить задачу по данной формуле вычис­ления периметра и т.п.). В процессе таких упражнений форми­руется понятие периметра многоугольника и умение находить его, а также развиваются пространственные и геометрические представления.

В процессе обучения элементарной геометрии школьников с нарушениями зрения следует учитывать следующие закономерности (Н.В. Клушина):

1. 
   Эффективность восприятия незрячими детьми различных геометрических фигур и тел зависит от их качественного своеобразия, а не от принадлежности к объемным или плоским формам;
   
2. 
   Применение системы математических и тифлографических приборов при обучении незрячих детей создает оптимальные условия для восприятия учебного материала, облегчает процесс формирования у незрячих детей правильных геометрических и пространственных представлений;
   
3. 
   Использование планиметрических и стереометрических чертежей во взаимодействии с моделями способствует эффективному формированию у незрячих школьников абстрактных представлений о геометрических формах;
   
4. 
   Комплексное выполнение и применение планов и макетов различных участков пространства стимулирует развитие пространственных представлений и ориентировку незрячих в окружающем пространстве.