Методика изучения уравнений, неравенств и их систем в курсе алгебры основного общего образования. Метод интервалов. Методика обучения решению текстовых задач в курсе математики основного общего образования
 Скачать 195.19 Kb. Скачать 195.19 Kb.
|
|
Методика изучения уравнений, неравенств и их систем в курсе алгебры основного общего образования. Метод интервалов. Методика обучения решению текстовых задач в курсе математики основного общего образования. Курс алгебры в школе можно представить, как развертывание некоторых содержательных линий, а именно числовая линия, в которой раскрывается понятия от натурального до комплексного числа; линия тождественных преобразований, она идет от алгебраических выражений до преобразований трансцендентных выражений; функциональная, которая развивается от линейных до трансцендентных функций; линия уравнений, неравенств и их систем, которая расвивается от линейных до трансцендентных; (с 2004 года) стохастическая линия, связанная с теорией вероятности и мат. статистикой. Все содержательные линии взаимосвязаны и развиваются в сотрудничестве. Рассмотрим, как развивается линия уравнений, неравенств и их систем в курсе математики в 5-11 классах.
Кроме данных тем в школе стоит рассматривать задачи с параметром. Они должны рассматриваться в следующем варианте: по мере изучения соответствующих типов уравнений учащихся следует знакомить с основными идеями их решения; 2) целесообразно работу нужно проводить в рамках элективного курса в старших классах. Линия уравнений, неравенств и их систем имеет содержательную основу для того, чтобы она помогает развиваться другим содержательным линиям; уравнения, неравенства используются как инструментарий для решения некоторых задач; учит языку математики и учит правильно применять моделирование. Понятие уравнения вводится либо в 5, либо в 6 классе при изложении соответствующего материала. Понятие вводится индуктивно и, как правило, выглядит следующим образом: «уравнением называют равенство, содержащее неизвестную букву, значение которой нужно найти». Возможны другие трактовки понятия уравнения, но указанное является наиболее оптимальным. Также рассматривается, что значит решить уравнение и что такое корень уравнения. Важно отметить, что все эти три понятия должны постоянно присутствовать на уроке при рассмотрения данной темы. Важное значение в курсе 5-6 классов имеют требования учителя к оформлению решения и требования к устной аргументации в процессе решения. В курсе 7 класса при изучении темы линейные уравнения учащиеся должны получить первые представления о свойствах решения уравнений как будущих теоремах о равносильных преобразованиях. Таких свойств два: обе части уравнения можно умножить или разделить на одно и то же число отличное от 0, и мы получим уравнение равносильное данному; если из первой части уравнения перенести в другую часть слагаемое, при этом изменив знак на противоположный, получим равносильное уравнение. Перед этим формулируется определение равносильных уравнений как уравнений, имеющих одно и то же множество корней. Данные свойства в 7 классе не доказываются. Их доказательства можно рассмотреть в 8 классе, если это позволяют возможности учащихся. Замечание: здесь стоит вопрос о необходимости иллюстрации учащимся неравносильных друг другу уравнений. Данный вопрос можно решить с помощью уравнения с модулем. При переходе к 8 классу возможно два способа построения изложения линии уравнений и неравенств. Первый более традиционный: вначале рассматриваются квадратные, дробно-рациональные, рациональные и иррациональные уравнения. А далее рассматривается блок, связанный с неравенствами. Второй подход связан с изучением неравенств на более раннем этапе, а именно до квадратных уравнений (Алимов). Данный подход имеет ряд преимуществ: перед изучением квадратных уравнений изучаются квадратные корни, рассматривается функция 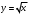 , решаются вопросы о множестве допустимых значений иррациональных выражений. Решить этот вопрос без владения решения хотя бы одного элемента невозможно; , решаются вопросы о множестве допустимых значений иррациональных выражений. Решить этот вопрос без владения решения хотя бы одного элемента невозможно;изучив решение линейных неравенств, в учебнике Алимова рассматривается вопрос о решении неравенств вида 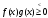 , где f, g– линейные функции или произведения линейных функций. Данное неравенство решается аналитически, пользуясь равносильными переходами, которые даются без доказательства. , где f, g– линейные функции или произведения линейных функций. Данное неравенство решается аналитически, пользуясь равносильными переходами, которые даются без доказательства.  При таком подходе есть возможность развивать культуру владения логическими операциями и/или осуществляется пропедевтика методов решения таких неравенств методом интервалов с точки зрения мотивации их решения. При решении квадратных уравнений важно выставить последовательность изложения материала. Важно, чтобы дети научились применять формулы Виета, формировать умения по использованию этих формул. У учащихся не только это вызывает затруднения, но и возникают трудности при решении неполных квадратных уравнений. В этой связи структуру изложения данного материала можно следующим образом: рассмотреть неполные квадратные уравнения вида 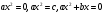 . Каждое из данных случаев разбирается. . Каждое из данных случаев разбирается.Рассматриваются полные квадратные уравнения, решаемые с помощью применения теорем «счастья»: Пусть дано уравнение вида 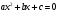 , тогда если , тогда если 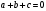 , то 1 – корень уравнения, а второй равен , то 1 – корень уравнения, а второй равен 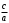 (формулируется без доказательства). (формулируется без доказательства).Пусть дано уравнение вида 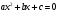 , если , если 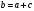 , тогда корнем уравнения является -1, а второй , тогда корнем уравнения является -1, а второй 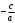 . .Если числа 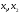 таковы, что таковы, что 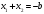 , а , а 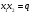 , то эти числа есть корни уравнения , то эти числа есть корни уравнения 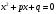 . И рассматриваются примеры на работу этих теорем. . И рассматриваются примеры на работу этих теорем.Замечание: детям однозначно говорится, что данные факты без доказательства, так как знания не позволяют их доказать. рассматриваются полные квадратные уравнения, решение через дискриминант и формулы полного квадрата и нахождение корней квадратных уравнений, а также через четное b, решаемое черед D1. рассматривается материал с прямой и обратной теоремой Виета Необходимо четко объяснить, сто теорема Виета для проверки корней, для нахождения второго корня, если известен первый. Обратная – подборка корней, составление уравнений по заданным корням. Теперь рассмотри особенности методики изучения дробно-рациональных уравнений. Определение: дробно-рациональным уравнением называется уравнение вида 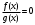 и уравнения, сводящиеся к ним, где f(x), g(x) – многочлены n-ой степени. и уравнения, сводящиеся к ним, где f(x), g(x) – многочлены n-ой степени.Данное определение необходимо давать учащимся, подчеркнув, что данный вид уравнения будем называть стандартным или каноническим. Можно выделить три способа рассуждений при решении: через равносильные переходы 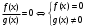 с использованием понятия ОДЗ. Следует отметить, что дробно-рациональные уравнения – это первый тип уравнений, в которых накладываются ограничения. Суть данного метода: 1) ОДЗ; 2) корни уравнения 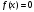 ; 3) проверяют принадлежат ли корня ОДЗ; 4) ответ. ; 3) проверяют принадлежат ли корня ОДЗ; 4) ответ.Переход к следствию 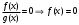 с обязательным заключительным этапом решения – проверка по исходному уравнению. с обязательным заключительным этапом решения – проверка по исходному уравнению. Таким образом, на примере дробно-рациональных уравнений появляется возможность существенным образом обогатить теоретический запас учащихся в области решения уравнений. Начинать разговор о методах решения дробно-рациональных уравнений лучше с первого способа, затем ко второму, потом к третьему. Решая данные уравнения первым способом, получая иррациональные значения x, дети убеждаются, что проверка крайне затруднительна и нужно искать другие подходы. Тем самым учитель мотивирует переход от первого ко второму, а затем к третьему способу решения. Немало важным понятием является понятие «посторонний корень», но лучше использовать выражение «число подозрительное на корень». Нужно объяснить учащимся , что ОДЗ может расширяться или наоборот сузиться. Например, 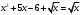 . ОДЗ: . ОДЗ: 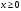 . При переносе из правой части в левую, выражения под знаком корня взаимоуничтожаются, а не сокращаются. Получаем уравнение вида . При переносе из правой части в левую, выражения под знаком корня взаимоуничтожаются, а не сокращаются. Получаем уравнение вида 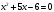 . Таким образом, ОДЗ у нас расширилась до всех действительных чисел. Далее происходит сравнение этих ОДЗ и записывается ответ. . Таким образом, ОДЗ у нас расширилась до всех действительных чисел. Далее происходит сравнение этих ОДЗ и записывается ответ.Следующий пример: 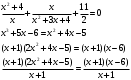 Каждый шаг фиксируется. Как видим ОДЗ изменилась. Стоит обратить внимание на то, что после сокращения она сузилась. Говоря о решении иррациональных уравнений нужно прежде всего иметь в виду, что данные уравнения продолжают работу по формированию умения решения квадратных уравнений. Надо понимать, что при возведении в квадрат обеих частей в квадрат (основной метод их решения), переходим к уравнению, которое является следствием исходного, то есть появляются посторонние корни. Учащимся 8 класса стоит сказать о всех нюансах решения данного типа уравнений. При решении иррациональных уравнений следует выделить: 1) 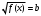 ; 2) ; 2) 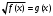 ; 3) ; 3) 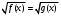 . Для каждого целесообразно дать теоремы о равносильных переходах. Особым образом следует выделить метод введения новой переменной, который хорошо демонстрируется на биквадратных уравнениях. Суть введения новой переменной стоит записать в тетради: . Для каждого целесообразно дать теоремы о равносильных переходах. Особым образом следует выделить метод введения новой переменной, который хорошо демонстрируется на биквадратных уравнениях. Суть введения новой переменной стоит записать в тетради:метод введения новой переменной нужен тогда, когда есть одинаковые выражения с переменной; при использовании этого метода все выражения, содержащие прежнюю переменную x, должны заменены на новую t,y. Стоит особое место выделить уравнениям, содержащими знак модуля. Вообще задачи с модулем вызывают большие затруднения у школьников. Впервые понятие модуля вводится при изучении отрицательных чисел в 6 классе. Именно с этого момента такие задания должны присутствовать на уроках, хотя бы в устной работе. В 6 классе учащиеся должны усвоит определение модуля через понятие расстояния и научиться им пользоваться при решении простейших уравнений 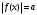 . Будет полезным уже здесь предлагать учащимся и неравенства вида . Будет полезным уже здесь предлагать учащимся и неравенства вида 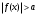 , иллюстрируя решение с помощью координатной прямой. , иллюстрируя решение с помощью координатной прямой.В 7 классе выходят на определение модуля аналитически без использования понятия модуль. 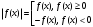 Данное определение целесообразно давать с использованием обозначения f(x) и после изучения темы «Функция». В 7 классе можно давать уже задания с модулем по сложнее. Так как могут получаться подозрительные корни, то лучше здесь использовать понятия следствия и равносильности. 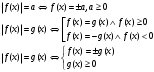 В 8 классе данные уравнения должны поставлены на систематическую основу, что означает рассмотреть с учащимися основные равносильные преобразования и основные равносильные переходы, метод промежутков для решения заданий с модулем. Алгоритм решения методом промежутков: находим нули подмодульных выражений наносим из на координатную прямую, на каждом из получившихся промежутков определяем знак подмодульных выражений рассматриваем задание на каждом промежутке, раскрывая модуль; все полученные значения x проверяем на принадлежность соответствующим промежутка. Теперь рассмотри методику изучения неравенств в курсе основной школы. Линейные неравенства начинаются рассматриваться в 8 классе, но возможно их рассмотрение ив 7 классе. Одним из ключевых моментов является вопрос изменения знака при умножении/делении на число или какое-либо выражение. Стоит вопрос, как эти правила сформулировать учащимся. Строго говоря, речь идет о доказательстве теорем о равносильных преобразованиях неравенств, что не является доступным для учащихся. Стоит заметить, что пропедевтическая часть начинается еще в 6 классе. Рассматривая какое-либо неравенство (a>b) и проводя аналогии между соответствующими свойствами числовых переменными, подводим учащихся к формулировке следующих правил: если дано верное числовое равенство a>b, то прибавляя к обеим частям c, то получим верное равенство a+c>b+c; если имеем верное равенство a>b и c>0, то получаем верное равенство ac>bc; если c<0, то получаем ac если есть a>b, c>d, то складывая их почленно, получим a+c>b+d (данное правило можно сформулировать: неравенства одного и того же знака можно почленно складывать); a>b, a,b>0, то 1/а<1/b. В сильных классах стоит доказать все эти свойства, а в слабых хотя бы одно. При переходе к рассмотрению неравенств с переменной, стоит сказать, что данные свойства выполняются и при работе с неравенствами с переменными. При решении линейных неравенств необходимо, чтобы дети свободно владели материалом о числовых промежутках и к началу изучения переходить от 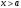 к к 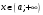 , и на координатной прямой показывать дугами и обратно; решение линейных неравенств проводить совместно с решением линейных уравнений, более того алгоритмы решения должны быть выучены. , и на координатной прямой показывать дугами и обратно; решение линейных неравенств проводить совместно с решением линейных уравнений, более того алгоритмы решения должны быть выучены.Тема квадратные неравенства рассматривается после темы «Квадратичная функция». Это связано с тем, что метод решения основан на свойствах квадратичной функции. Алгоритм решения 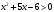 рассмотрим функция 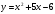 область определения 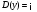 найдем нули функции x=1, x=-6 рисуется координатная прямая     + - + -6 1 x 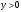 при при 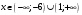 Ответ. По мере изучения темы и видя, что учащиеся усвоили образец оформления, можно переходить к упрощенной форме записи решения. 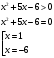     + - + -6 1 x 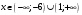 Ответ: 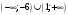 . .Первый образец является обязательным, так кая является пропедевтическим. Можно так же решать такие неравенства без ссылки на квадратичную функцию. В ряде учебников квадратные неравенства рассматриваются методом интервалов. 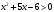 рассмотрим функция 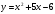 (иногда отсутствует) (иногда отсутствует)  нули функции 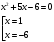   + - +    (Знаки расставляются путем пробных точек) Ответ: 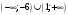 Решение квадратных неравенств методом интервалов не совсем уместен, так как использование графика квадратичной функции решает проблему расстановки знаков; метод интервалов является основным методом решения неравенств, и схема его формирования должна усвоена жестким образом; вышеуказанный вариант через функцию готовит к восприятию метода интервалов. Говоря о решении дробно-рациональных неравенств необходимо дать определения дробно-рациональным уравнениям, рассмотреть алгебраический и функционально-графический метод решения. Определение: неравенство вида 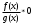 , где fиg – многочлены от переменной x,а , где fиg – многочлены от переменной x,а 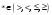 называют дробно-рациональным неравенством. называют дробно-рациональным неравенством.Понятие можно вводить как дедуктивно, так и индуктивно. Отметим, что умение решать дробно-рациональные неравенства базируются на умении выполнять тождественные преобразования с алгебраическими дробями. В этой связи учителю целесообразно провести актуализацию знаний и умений учащихся по данной теме, предварительно задав соответствующий материал ка часть домашней работы. Аналитический или алгебраический метод решения дробно-рациональных неравенств основан на теореме о равносильных преобразованиях 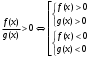 Стоит отметить, что такой подход к решению стоит рассматривать в классах с достаточно математической подготовкой. Функционально-графический метод (метод интервалов) является основным при решении неравенств в школе, поэтому должен быть усвоен всеми учащимися. В зависимости от уровня подготовленности класса можно выбрать индуктивный или дедуктивный метод изложения материала. Индуктивный предполагает рассмотрение 2-3 примеров до того, как рассматривать задания, в которых встречаются все нюансы в процессе решения. Дедуктивный позволяет рассматривать решение сразу с такого примера. При индуктивном методе система решений выглядит примерно так: 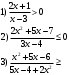 Решив данные задания, учителю стоит обобщить те особенности, которые объединяют данные упражнения. Например, дети могут сказать, что у данных заданиях знаки чередуются, в качестве ответов промежутки или их объединения. Четвертым примером учитель как раз опровергает данные представления. Алгоритм оформления решения и рассуждения в точности повторяет рассуждения при решении квадратных уравнений. Алгоритм состоит из 5 шагов, которые ученик должен фиксировать в тетради. Метод интервалов применяется тогда и только тогда, когда справа 0 (на подготовительном этапе). 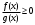 Рассмотрим функцию 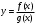 Найдем 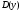 . .Найдем нули функции. На координатной прямой наносим 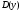 На координатной прямой наносим нули функции и определяем знаки на полученных промежутках. Рисуется кривая знаков, записывается ответ. Необходимо обратить внимание учащихся, что знаки, которые расставляем, относятся к интервалам и не передаются на концевые точки. Принадлежат ли концевые точки множеству истинности или нет определить нужно отдельно и приучить к этому учащихся. Возможно здесь рассмотрение и решение иррациональных неравенств, хотя это и не входит в материал программы. Что касается методики обучения решению систем уравнений и неравенств, то здесь основной задачей выступает знакомство учащихся с методами их решения. Выделяют 4 метода решения: метод подстановки; метод алгебраического сложения; метод введения новой переменной; графический метод. Методика обучения решению текстовых задач в курсе математики основного общего образования. Текстовые задачи встречаются с 1 по 11 класс. Почему такая важность текстовых задач. Именно при решении текстовых задач мы более-менее ясно демонстрируем возможности математики для каких0либо прикладных задач (в том числе и бытовых задач). Именно на примере текстовых задач демонстрируется детям ключевой метод познания – метод математического моделирования. При рассмотрении вопроса о решении текстовых задач следует разделить вопрос с точки зрения метода решения. Выделяют два метода: арифметический (по действиям), алгебраический (с помощью уравнения, неравенства или системы). Первый, с которым знакомятся школьники – арифметический. С точки зрения вопроса о том, когда нужно знакомить с алгебраическим способом позиции ученых разделяются. Одни говорят, что раннее использование алгебраического способа мешает учить школьников логическим рассуждениям, основанным на образной стратегии. Например, у Бунимовича в 5 классе нет уравнений совсем, поэтому задачи решаются по действиям. Мордкович и Виленкин с 5 класса учат способу решения с помощью уравнений. Главное здесь не то, когда лучше знакомить с тем или иным методом решения текстовых задач, а то, как удобнее и понятнее ребенку. Все равно рано или поздно придет время, когда некоторые задачи нельзя решить с помощью уравнения. Следующий важный момент – это то, что у учащихся возникают проблемы с представлением ситуации в задаче. Классификация задач: На движение На работу На сплавы, смеси, раствор На товарно-денежные отношения На количественные отношения На проценты На прогрессии Первые три типа носят главную роль, к ним можно присоединить еще задача на прогрессии. 1 тип – движение S=Vt, 2 тип – производительность труда A=pt, 3 тип – концентрация n=m/M. Схема работы над задачей: Актуализация опорных знаний (о типах текстовых задач). Чтение задачи, работа с условием (прочитать, какой тип задачи, какие параметры, как вязаны). Усвоение условия (пересказ условия учеников, вопросы учителя: сколько героев, сюжетов). Этап схематизации (таблица, график-схема, рисунок) – ключевой этап. Установление связей между величинами, представленных в задаче (уравнение). Решение полученных уравнений (математическая модель). Интерпретация (перевод с математического языка на язык задачи). Проверка выполненного решения (составление и решение обратной задачи, по условию задачи проходишь все условия, не приводя противоречий). Ретроспективный анализ (ученик научился самостоятельно решать задачи другого типа). Примеры решения текстовых задач. Например, предлагалась следующая задача. Две машины выехали одновременно из одного пункта в одно направление. Скорость первой машины – 50 км/ч, второй – 40 км/ч. Спустя пол часа из того же пункта в том же направлении выехала третья машина, которая обогнала первую машину на 1,5 ч позже, чем вторую. Найдите скорость третей машины. Для решения данной задачи предлагалось сделать рисунок, по нем составить систему уравнений и решить ее.           V2 V1 1)   B A    V3 V1 V2     B D C A 20 км 25 км t=0,5 ч       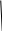   V1 V2      V3 F E B A  V1     B A V3 H tEF=1,5 ч Основываясь уравнением движения 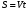 , получим следующие данные для каждого из рисунков. , получим следующие данные для каждого из рисунков.2) AC=20 км AD=25 км AE=V3t=40(t+0,5) AH=V3(t+1,5)=50(t+2) В результате пришли к системе уравнений с двумя неизвестными: 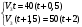 Следующая задача, которую можно решить нетривиальным способом, на сплавы и смеси. Решение оформляется в прямоугольниках, который в полной мере характеризует каждый сплав или смесь. Например, имеется 735 грамм 16 % раствора йода в спирте. Нужно получить 10% раствор йода. Сколько грамм спирта нужно прибавить к имеющемуся раствору.     735 г m n1=16% (735+x) г m n2=10% x-? 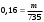 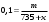 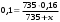 Таким образом можно решать любую текстовую задачу. Но многие учащиеся все равно предпочитают решать задачи алгебраическим методом, обозначая за x что требуется найти в задаче. |
