22. Методика работы над текстовой арифметической задачей на урок. Методика работы над текстовой арифметической задачей на уроке математики в школе для обучающихся с умственной отсталостью
 Скачать 144.68 Kb. Скачать 144.68 Kb.
|
|
Методика работы над текстовой арифметической задачей на уроке математики в школе для обучающихся с умственной отсталостью Текстовой арифметической задачей называют словесно сформулированное требование нахождения числового значения искомой величины по известным заданным величинам и связывающим эти величины зависимостям, выраженным в задаче явно или косвенно. В методике работы над любой арифметической задачей можно выделить следующие этапы: 1. Работа над содержанием задачи Большое внимание следует уделять работе над содержанием задачи, т. е. над осмыслением ситуации, изложенной в задаче, установлением зависимости между данными, а также между данными и искомым. Последовательность работы над усвоением содержания задачи: а) разбор непонятных слов или выражений, которые встретятся в тексте задачи; б) чтение текста задачи учителем и учащимися; в) запись условия задачи; г) повторение задачи по вопросам; д) воспроизведение одним из учащихся полного текста задачи. Текст задачи первоначально рассказывает или читает учитель, а, начиная со 2-го класса, его могут читать и ученики по учебнику или по записи на доске. Читать задачу нужно выразительно, выделяя голосом математические выражения, главный вопрос задачи, делая логические ударения на тех предложениях или сочетаниях слов, которые прямо указывают на определенное действие (Например, учительница разложила 12 карандашей в 2 коробке поровну; купили 9 тетрадей по 4 рубля). Между условием задачи и вопросом следует сделать паузу, если вопрос стоит в конце задачи. Выразительному чтению текста задачи следует учить учеников. Нужно помнить, что школьники с нарушением интеллекта, если их этому специально не учить, не могут самостоятельно правильно прочитать задачу, не могут расставить логические ударения, даже выделить вопрос задачи, если он стоит в начале или середине задачи. Задачу следует иллюстрировать. Для иллюстрации задач в 1—2-х классах учителя прибегают к предметной иллюстрации. Если в 1-м классе текст задачи иллюстрируется с помощью предметов или рисунков, то в конце 1-го и во 2-м классе надо учить учащихся заменять элементы предметных множеств их символами. Наряду с конкретизацией содержания задачи с помощью предметов, трафаретов и рисунков в практике работы учителей коррекционной школы широкое распространение получили следующие формы записи содержания задачи: Сокращенная форма записи, при которой из текста задачи выписывают числовые данные, и только те слова и выражения, которые необходимы для понимания логического смысла задачи. Вопрос задачи записывается полностью. Например, «Для посадки в парк привезли 25 ёлочек, а лип на 20 больше. Сколько всего деревьев привезли для посадки?» Сокращенная запись: «Ёлочек – 25, лип на 20 больше. Сколько всего деревьев?» Сокращенно-структурная форма записи, при которой каждая логическая часть задачи записывается с новой строки. Например,   на 20 штук больше «Ёлочек – 25 штук  Лип – ? Сколько всего деревьев?» Схематическая форма записи. Это запись содержания задачи в виде схемы. В схеме желательно сохранить пропорции, соответствующие числовым данным. Например,   25 ёлочек   ? на 20 штук больше 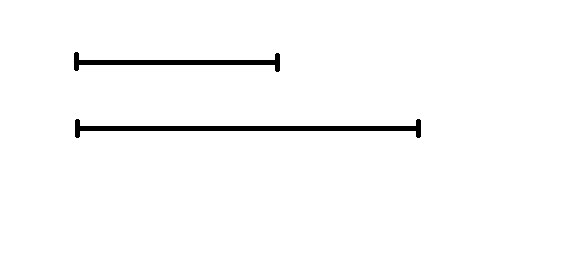 Г  рафическая форма записи. Это запись содержания задачи в виде чертежа, диаграммы. Удобнее всего в графической форме записывать задачи на движение. Например, рафическая форма записи. Это запись содержания задачи в виде чертежа, диаграммы. Удобнее всего в графической форме записывать задачи на движение. Например, 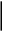 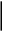       В 2 раза больше 18 км/ч Время в пути 3 часа   ? После ознакомления учащихся с текстом задачи учитель сам дает краткую запись содержания задачи на доске, учащиеся записывают ее одновременно с учителем в тетрадь. Лучшему восприятию и пониманию задачи способствует ее повторение по вопросам. Форма вопросов при повторении задач меняется: сначала учитель задает конкретные вопросы, а затем обобщенные. Например: «В коробке было 3 красных карандаша. Вова положил туда еще 2 зеленых карандаша. Сколько всего карандашей в коробке?» Повторение задачи по вопросам: «О чем эта задача? Какого цвета карандаши? Сколько красных карандашей лежало в коробке? Покажите цифрой». 2. Поиск решения задачи На этом этапе учащиеся, отвечая на вопросы учителя, подводятся к составлению плана решения задач и выбору действий. Намечают план и последовательность действий — это следующий этап работы над задачей. Выбор действия при решении задачи определяется той зависимостью, которая имеется между данными и искомыми в задаче. Зависимость эта правильно может быть понята в том случае, если ученики поняли жизненно-практическую ситуацию задачи. С этой целью учитель проводит беседу с учащимися, которая называется разбором задачи. Разбор задачи можно начинать с числовых данных (сверху) и вести учащихся к главному вопросу задачи. К двум числовым данным, которые вычленяются из условия задачи, подбирается вопрос. Например: «Школьники на пришкольном участке посадили 17 грядок помидоров, по 30 штук на каждой, и 20 грядок капусты, по 25 штук на каждой. Сколько всего штук рассады посадили?». Беседу учитель проводит так: «Известно, что посадили 17 грядок помидоров, по 30 штук на каждой. Что можно узнать по этим данным? Каким действием? (Умножением. Надо 30 шт. умножить на 17.) Почему? Разбор задачи можно начинать от главного вопроса задачи (снизу). При этом к вопросу учащиеся должны подобрать 2 числа. Беседу можно построить так: «Можно ли сразу ответить на вопрос задачи? Почему нет?» При разборе уже знакомых учащимся задач не следует прибегать к многословным рассуждениям. Иногда достаточно поставить перед учащимися один-два узловых вопроса, чтобы путь решения задачи был ученикам ясен. 3. Решение задачи Опираясь на предыдущий этап, в процессе которого учащиеся осуществляли поиск решения задачи, они готовы устно сформулировать вопросы задачи и назвать действия. Учитель спрашивает: «Во сколько действий задача? Какой первый вопрос? Каким действием можно ответить на этот вопрос?» И т. д. Далее устно составляется план и намечается последовательность действий. «Итак, — спрашивает учитель, — какой первый вопрос? Какое действие? Какой второй вопрос?» И т. д. После этого учащимся предлагается записать решение. Действие записывается в середине строки, чтобы отличить его от записи примера. При этом учитель учит учащихся давать краткое пояснение к выполняемому действию (устно). По мере изучения букв учащихся учат записывать решение задачи с наименованием. Начиная со 2-го класса вводится запись решения задач с пояснением. Например: «Оля купила 5 тетрадей в клетку и 6 тетрадей в линию. Сколько всего тетрадей купила Оля?» Решение этой задачи записывается так: 5 т.+ 6 т. = 11 т. (купила Оля) При записи сложных задач могут использоваться следующие формы записи: Задача: Для озеленения сквера в первый день привезли 50 кустов сирени, а во второй – 46. За 2 дня посадили 84 куста. Сколько кустов осталось посадить? а) запись арифметических действий и ответа задачи; 1)50+46=96 к. 2)96-84=12 к. Ответ: 12 кустов осталось посадить. б) запись решения с пояснением того, что найдено в результате каждого действия; 1)50+46=96 кустов сирени привезли. 2)96-84=12 кустов сирени осталось посадить. Ответ: 12 кустов осталось посадить. в) запись решения с вопросами (вопросы и действия чередуются). В конце записывается ответ; 1) Сколько кустов сирени привезли для озеленения? 50+46=96 к. 2) Сколько кустов осталось посадить? 96-84=12 к. Ответ: 12 кустов осталось посадить. г) запись сначала только плана решения, затем соответствующих действий или, наоборот, запись сначала действий, а затем плана решения задачи. В конце записывается ответ. План: 1) Сколько кустов сирени привезли для озеленения? 2) Сколько кустов осталось посадить? Решение: 1)50+46=96 к. 2)96-84=12 к. 4. Формулировка ответа Форма ответа может быть краткой и полной. Например, краткая форма ответа: 12 к. или 12 к. сирени; полная форма ответа: 12 к. сирени осталось посадить. 5. Проверка решения задачи Так как функция контроля у школьников с нарушением интеллекта ослаблена, то проверка решения задач имеет не только образовательное, но и коррекционное значение. В младших классах необходимо: 1. Проверять словесно сформулированные задачи, производит действия над предметами, если, конечно, это возможно. Например: «У ученика было 15 р. Он купил 5 тетрадей по 2 р. Сколько денег у него осталось?» После решения задачи ученик берет по 2 р. 5 раз и считает, сколько всего денег. Потом из 15р. вычитает 10 р., получается 5 р. 2. Проверять реальность ответа (соответствие его жизненной действительности). 3. Проверять соответствие ответа условию и вопросу задачи. (О чем спрашивается в задаче? Получили ли ответ на вопрос задачи?) Проверка решения задачи другим способом ее решения возможна с 4-го класса. Для контроля правильности решения задачи используются и некоторые элементы программированного контроля. Например, учитель пишет на доске ответы конечного и промежуточных действий, только не в том порядке, который необходим при решении задачи; учащиеся (при самостоятельном решении) сверяют ответы промежуточных действий и «запрограммированные» ответы. Этот прием очень полезен тем, что ученик сразу получает подкрепление правильности или, наоборот, ошибочности своих действий. При ошибочности решения он ищет новые пути решения. 6. Последующая работа над решенной задачей Учитель коррекционной школы зачастую не может быть уверен, что решение задачи понято всеми учениками. Поэтому очень полезно провести работу по закреплению решения этой задачи. Работа по закреплению решения задачи может быть проведена различными приемами. 1. Ставятся узловые вопросы по содержанию задачи. 2. Предлагается рассказать весь ход решения задачи с обоснованием выбора действий. 3. Ставятся вопросы к отдельным действиям или вопросам. Для учащихся коррекционной школы важно не количество решенных аналогичных задач, а понимание предметной ситуации и зависимости между данными. Этой цели и служит последующая работа над решенной задачей, которую можно рассматривать как важный прием, формирующий умение решать задачи данного вида. Рассмотрим несколько вариантов последующей работы над решенной задачей: 1. Изменение отношений между данными условия задачи выяснение, как это изменение отразится на решении задачи; 2. Изменение вопроса задачи; 3. Изменение условия задачи, привнесение в него дополнительного данного или изъятие какого-либо данного; 4. Изменение числовых данных, сюжета задачи, решение задачи, аналогичной данной. Конечно, не над каждой решенной задачей следует проводить такую последующую работу. Однако надо помнить, что это один из полезных приемов, который учит самостоятельному решению задач, пониманию зависимости между данными, между данными и искомым, а также тому, как эта зависимость отражается на выборе арифметических действий. |
