Метрологические характеристики методов анализа. Метрологические характеристики методов анализа содержание

• Название: Метрологические характеристики методов анализа содержание
• Анкор: Метрологические характеристики методов анализа.doc
• Дата: 17.04.2018
• Размер: 0.91 Mb.
• Имя файла: Метрологические характеристики методов анализа.doc
• Тип: Документы; #18160
• страница: 6 из 7

Погрешность суммы и произведения

В химико-аналитических расчетах довольно часто приходится использовать разности измеренных величин, их суммы, произведения и т.д. Например, по разности двух взвешиваний определяют массу осадка в гравиметрическом анализе, по разности оптических плотностей находят светопоглощение компонента и т.д. Поэтому расчет погрешности разности или произведения имеет прямой практический интерес.

В теории вероятности доказывается, что дисперсии независимых случайных величин обладают свойством аддитивности, которого стандартные отклонения не имеют. Поэтому дисперсия суммы или разности нескольких величин Х₁, Х₂... будет равна:

(6.1)

В случае произведения или дроби суммируются дисперсии относительных погрешностей: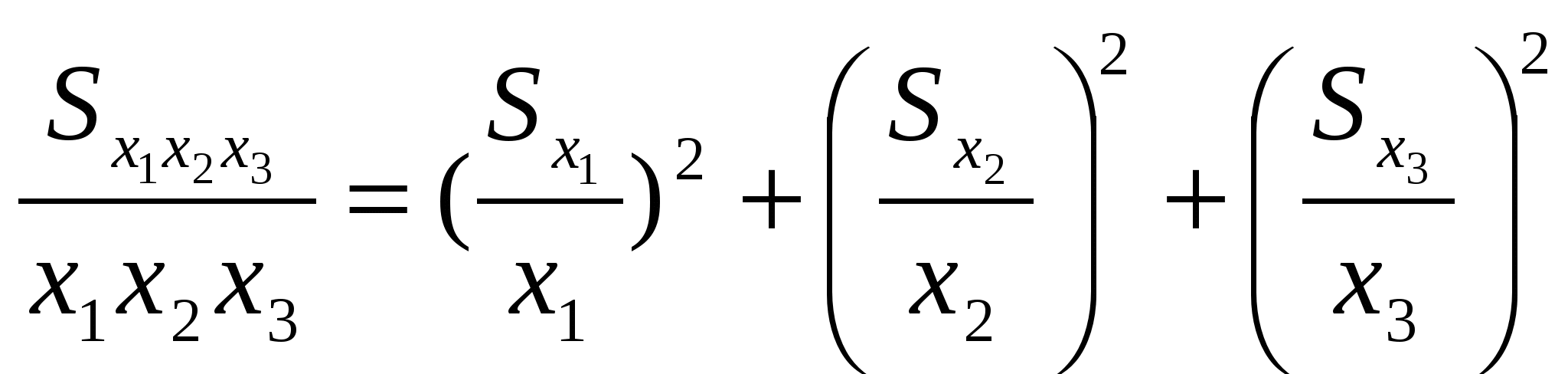

(6.2)

Средняя квадратичная погрешность суммы или разности может быть рассчитана по уравнению:

Погрешность произведения или дроби рассчитывается по дисперсиям относительной погрешности: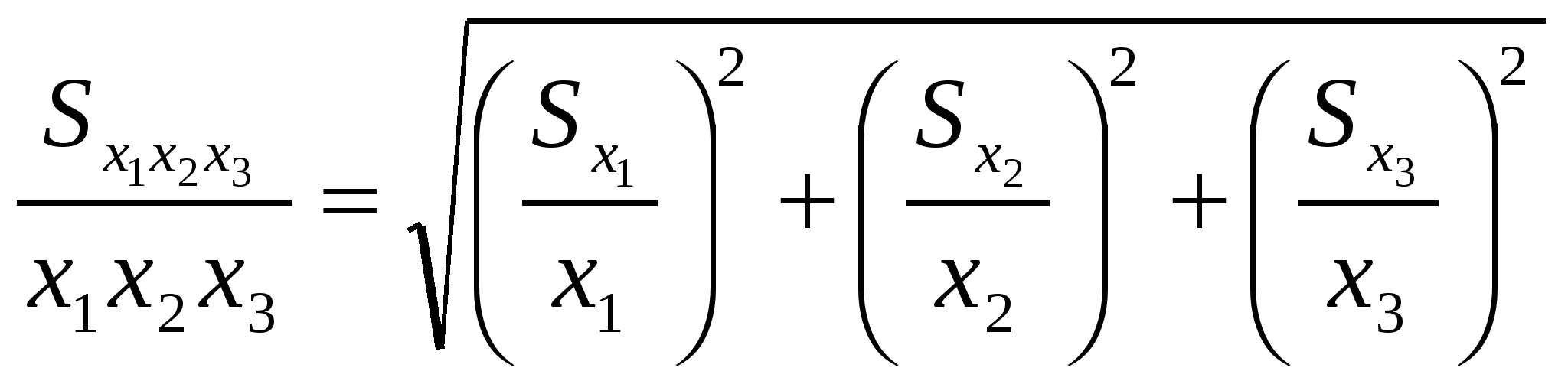


В случае стохастической (вероятностной) или другой связи между величинами необходим учет коэффициента корреляции, однако этот вопрос выходит за рамки нашей программы. Следует обратить внимание на то, что эффективное уменьшение погрешности суммы или произведения может быть достигнуто за счет уменьшения тех погрешностей, которые дают наибольший вклад в суммарную погрешность, т.е. имеют наибольшее значение. Практическое применение этих соотношений рассматривается далее при обсуждении различных методов анализа.

7. Обнаружение промахов

В ряду нескольких параллельных определений нередко обнаруживается результат анализа, резко отличающийся от других результатов и от среднего арифметического всей серии. Произвольное отбрасывание измерения, которое является «слишком» высоким или «слишком» низким, может существенно исказить результат анализа, так же как и включение ошибочных данных в расчет среднего арифметического. Выявление грубых ошибок (промахов) остается достаточно деликатной задачей. Дляобнаружения промахов в ряду параллельных определений при небольшом числе опытов может быть использован критерий Q:

(7.1)
,
где x₁ – подозрительно выделяющееся (сомнительное) значение; х₂– соседнее с ним значение; R– размах варьирования, равный разности между максимальным и минимальным значениями х в рассматриваемом ряду.

Рассчитанная по уравнению (7.1) величина Q сравнивается с Q_табл. – табличным значением критерия при данных вероятности и числе степеней свободы. Его можно найти, например, в таблице 2. Если Q>Q_табл., подозреваемый результат является грубо ошибочным и его следует исключить при расчете среднего арифметического.

Таблица 2

Числовые значения Q_табл.

Число степеней свободы, f=n-1	Критерий Qтабл.
	Доверительная вероятность, Р
	0,90	0,95	0,99
2	0,89	0,94	0,99
3	0,68	0,77	0,89
4	0,56	0,64	0,76
5	0,48	0,56	0,70
6	0,43	0,51	0,64
7	0,40	0,48	0,58
8	0,37	0,46	0,53
9	0,34	0,44	0,48

Если бы, например, при определении содержания олова в бронзе пятый результат анализа показал, что в бронзе содержатся5,10 % Sn, его можно было бы заподозрить как ошибочный и проверить по критерию Q в соответствии с уравнением (7.1):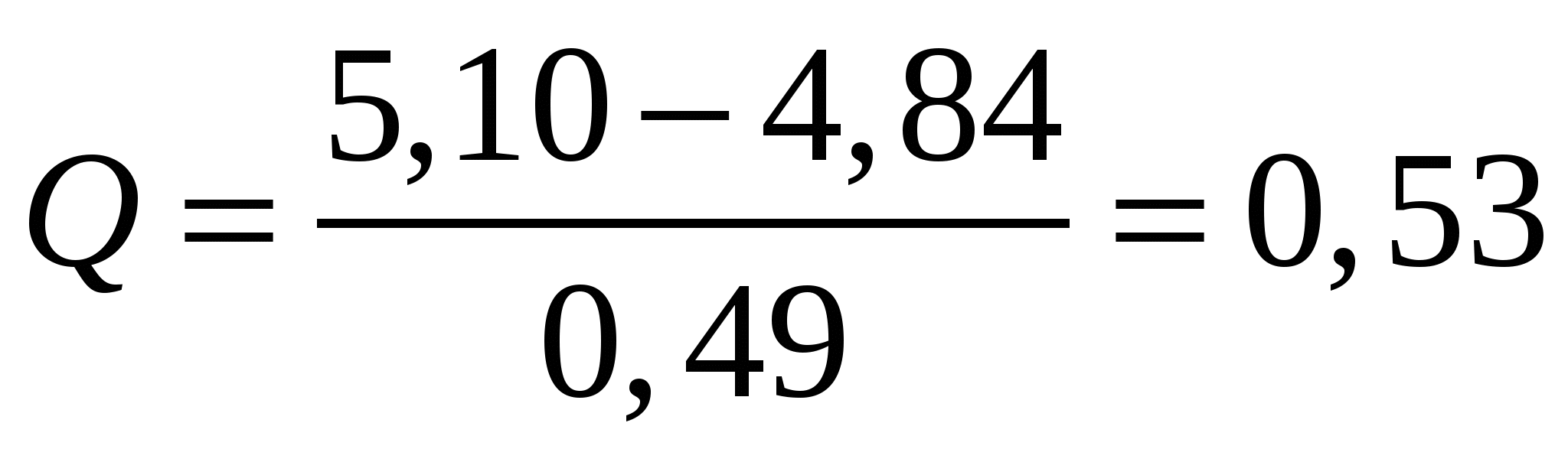

Это меньше, чем Q_табл.=0,64 (для Р=0,95 и f=4), поэтому результат 5,10 % Sn грубым промахом не является.

В сомнительных случаях, например, если величина Q, рассчитанная по уравнению (7.1), близка к Q_табл. применяют более точные критерии, требующие расчета стандартного отклонения. Подозрительный результат х₁является грубым промахом, если:

(7.2)


или

(7.3)

Коэффициент 3 в уравнении (7.2) иногда заменяют на 4.

Рекомендуется также использовать способ, основанный на расчете отношения V_mах:

(7.4)

Если рассчитанное по уравнению (7.4) значение V_mах будет превышать табличное значение этой величины, то результат х₁следует рассматривать как промах и не учитывать его при расчете среднего и дальнейших вычислениях.

Необходимо отметить, что никогда не следует отбрасывать сомнительный результат только «по интуиции», без использования какого-либо количественного критерия. Это имеет особое значение при малом числе измерений, когда отбрасывание вызывает существенное изменение средней величины.