Анализ экспериментальных данных показывает, что большие по значению погрешности наблюдаются реже, чем малые. Отмечается также, что при увеличении числа наблюдений одинаковые погрешности разного знака встречаются одинаково часто. Эти и некоторые другие свойства случайных погрешностей описываются нормальным распределением или уравнением Гаусса:
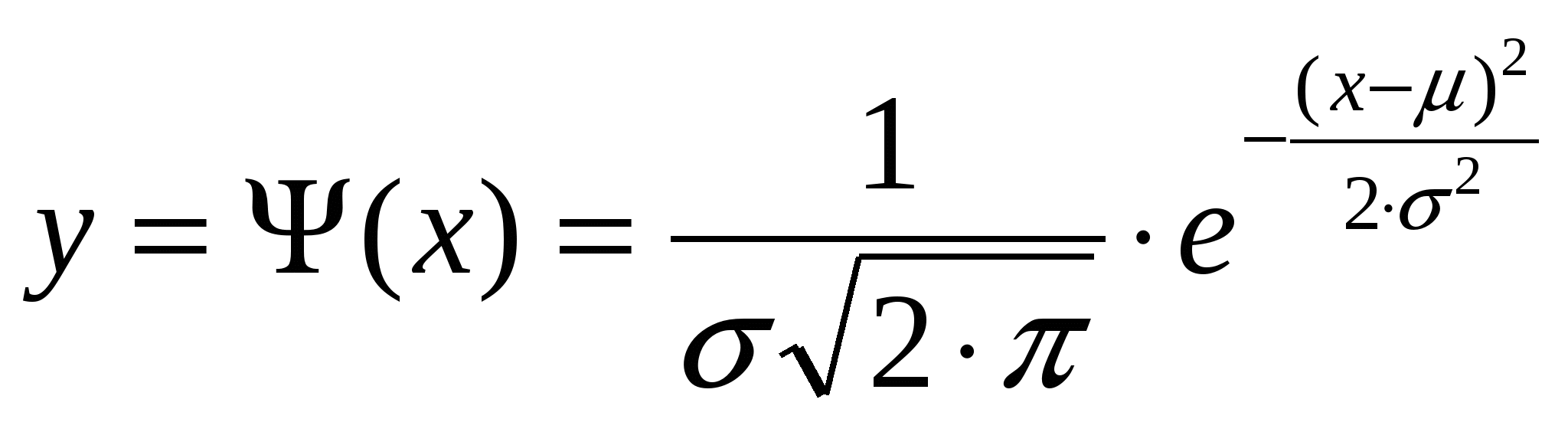
(4.1)
где 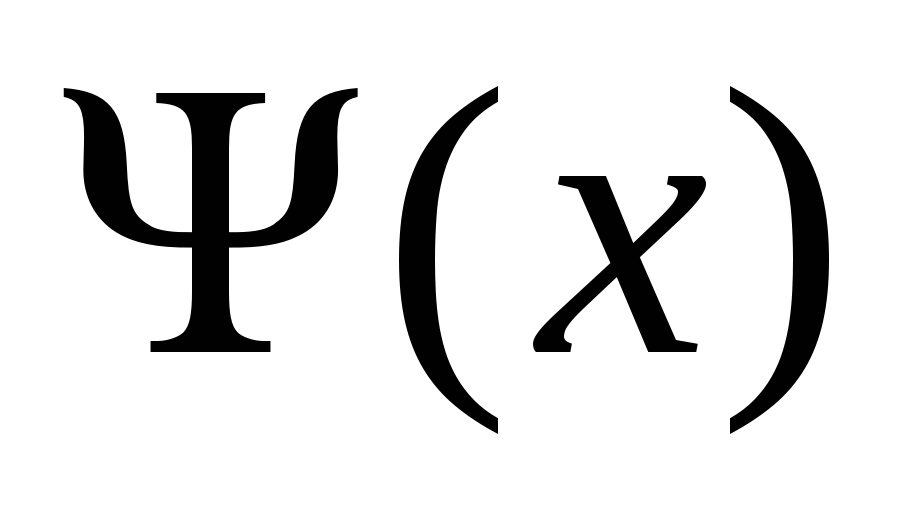 – плотность вероятности; х – значение случайной величины; μ – генеральное среднее (математическое ожидание); σ2 – дисперсия. – плотность вероятности; х – значение случайной величины; μ – генеральное среднее (математическое ожидание); σ2 – дисперсия.
Равные по площади кривые нормального распределения приведены на рис. 4.1. Как видно, чем больше стандартное отклонение (дисперсия), тем более пологой становится кривая.
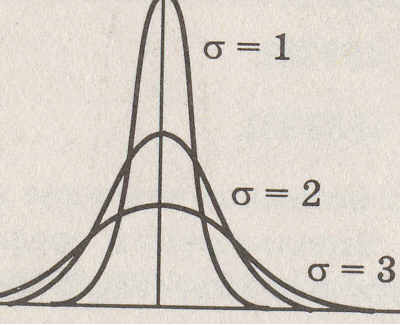
Рис. 4.1. Кривые нормального распределения при различной средней квадратичной погрешности
Величины 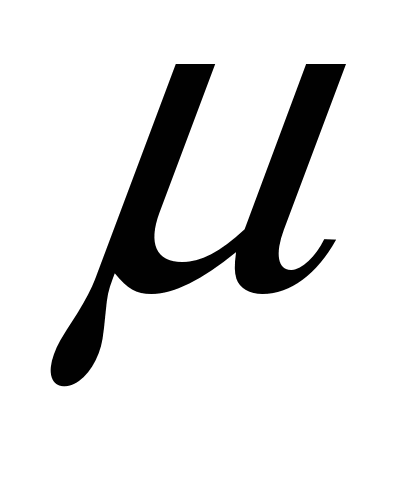 и и  называют параметрами распределения. Уравнение (4.1) описывает плотность вероятности. Коэффициент называют параметрами распределения. Уравнение (4.1) описывает плотность вероятности. Коэффициент 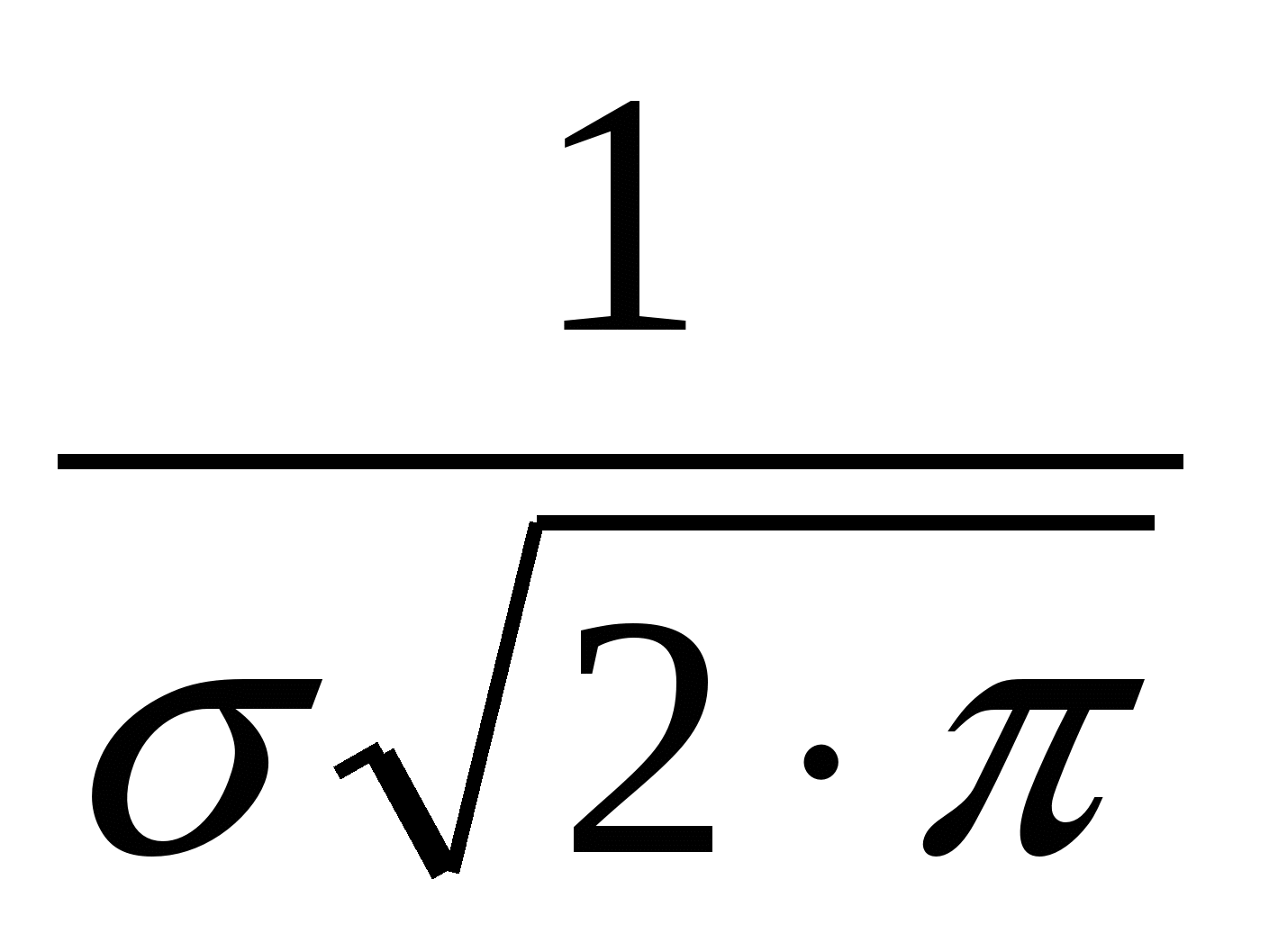 выбран так, чтобы вероятность попадания случайной величины Х в интервал – выбран так, чтобы вероятность попадания случайной величины Х в интервал –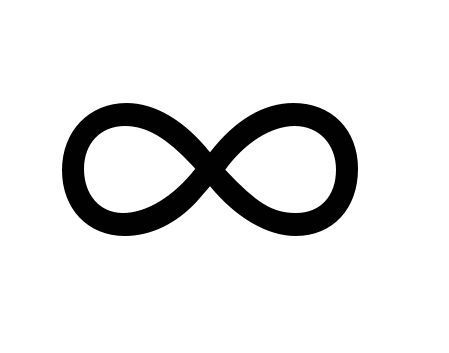 <X< <X<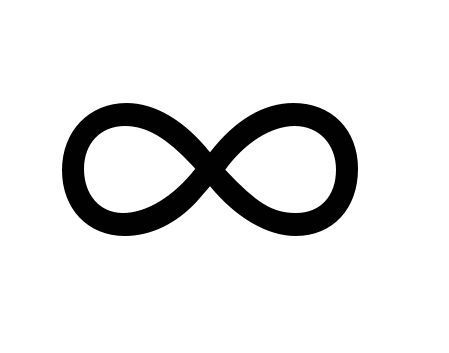 была равна единице: была равна единице:
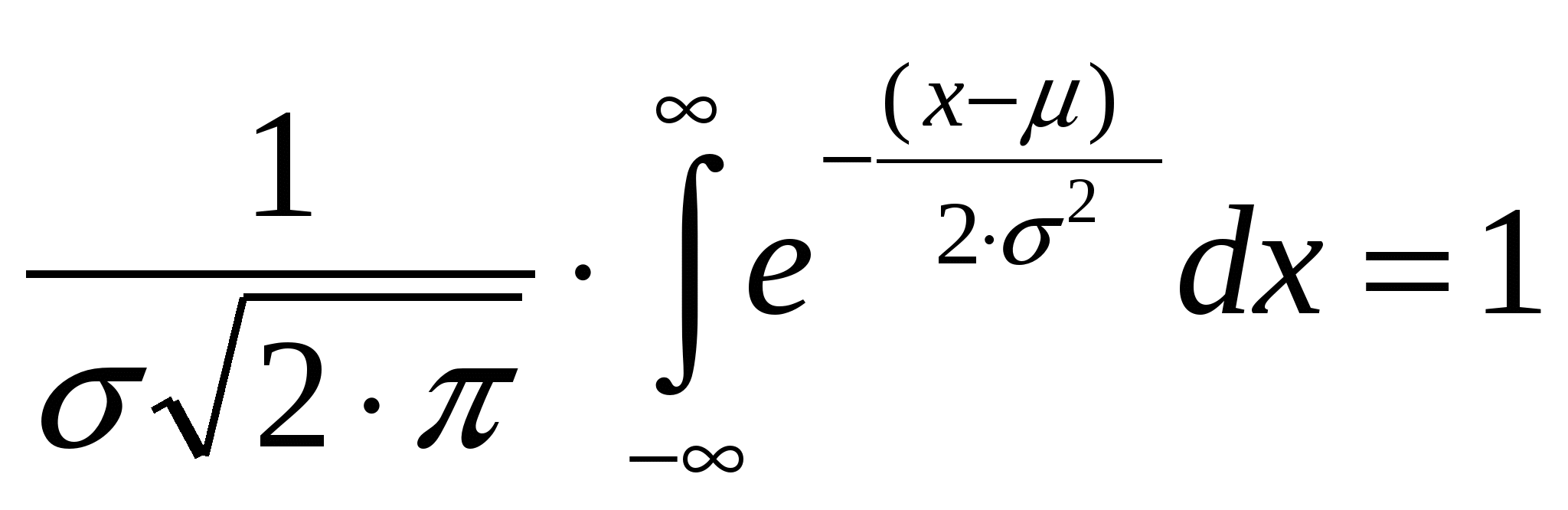
(4.2)
При любых значениях 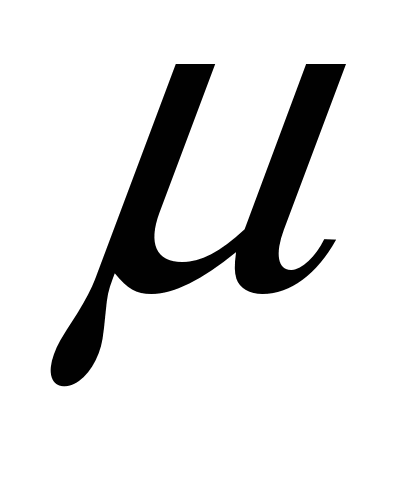 и и  площадь, ограниченная кривой (4.1) и осью абсцисс, равна единице. Очевидно, если через Х1и Х2провести ординаты, то случайная величина Х попадает в интервал Х1 < Х < Х2 с вероятностью: площадь, ограниченная кривой (4.1) и осью абсцисс, равна единице. Очевидно, если через Х1и Х2провести ординаты, то случайная величина Х попадает в интервал Х1 < Х < Х2 с вероятностью:
1 Х2 _(х - )2
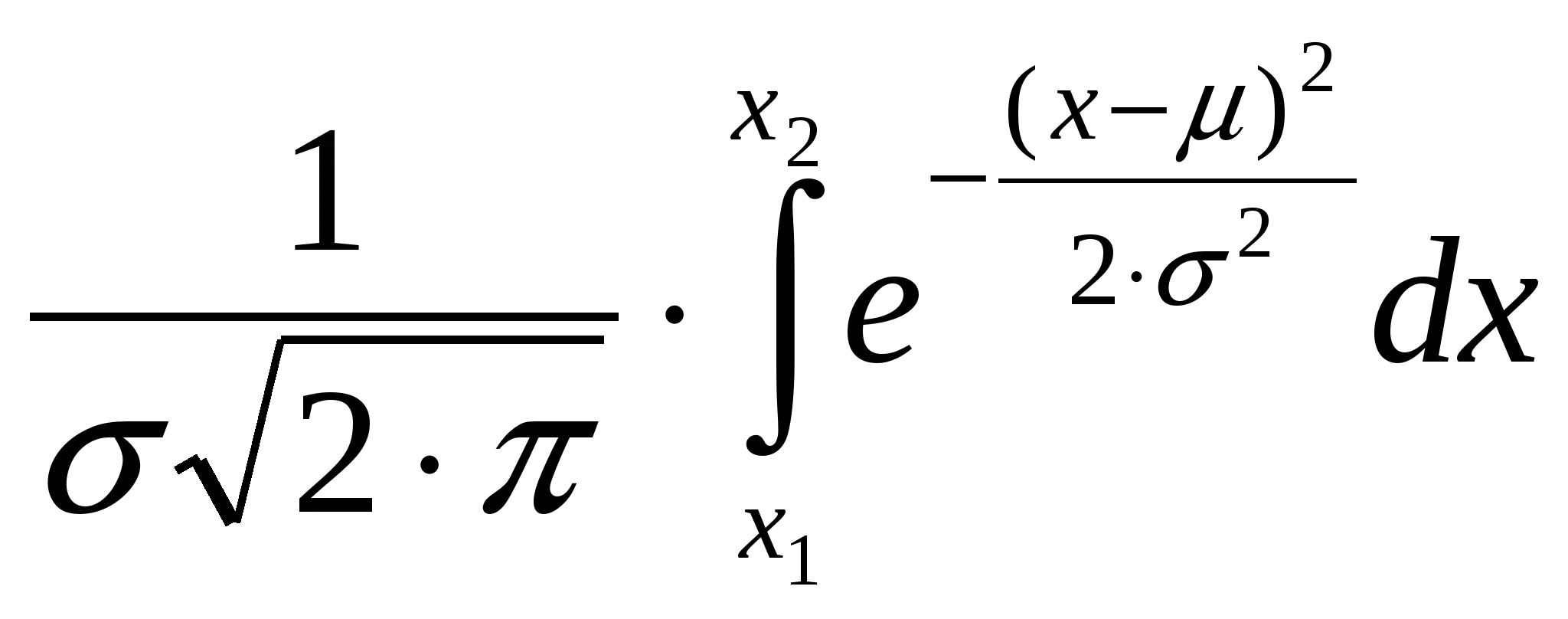
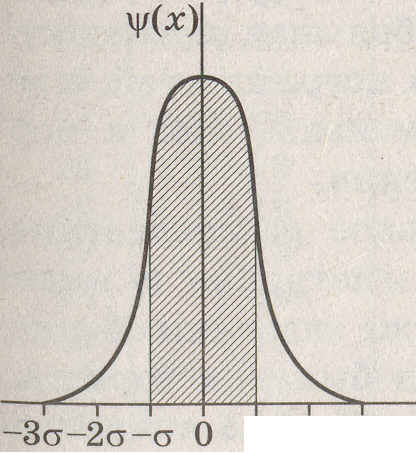
Расчеты показывают, что интеграл (4.2) в пределах от 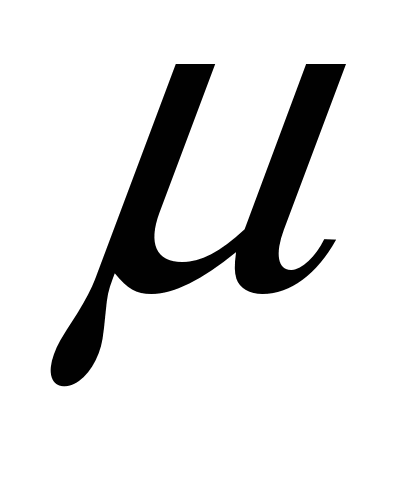 – – до до 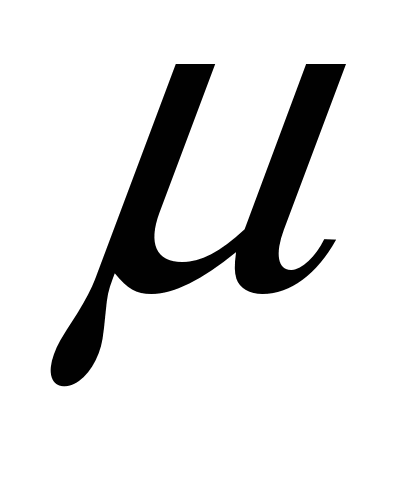 + + составляет 68,3 % общей площади, в пределах составляет 68,3 % общей площади, в пределах 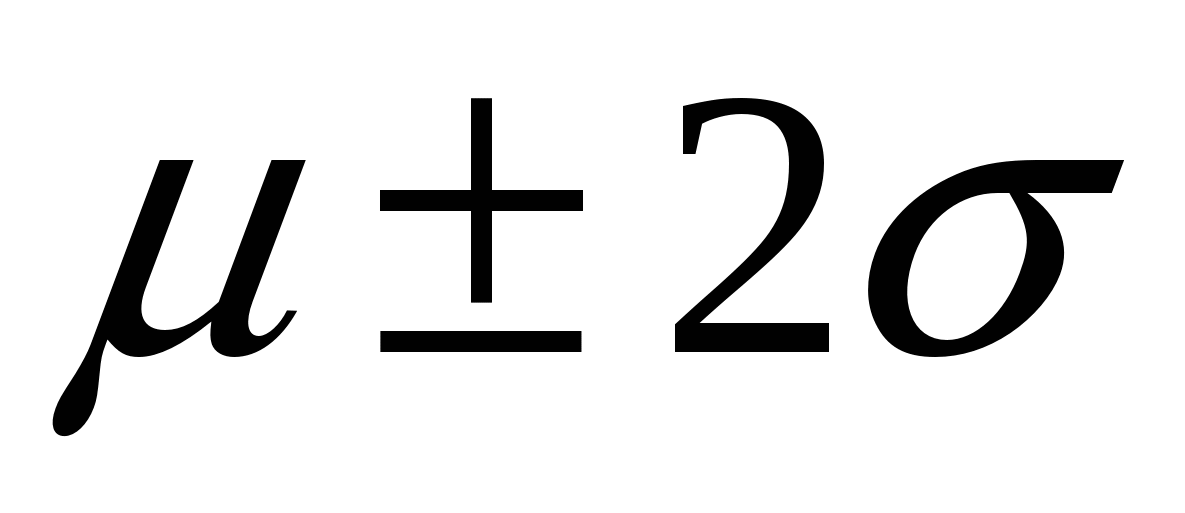 уже 95 % ее, а при уже 95 % ее, а при 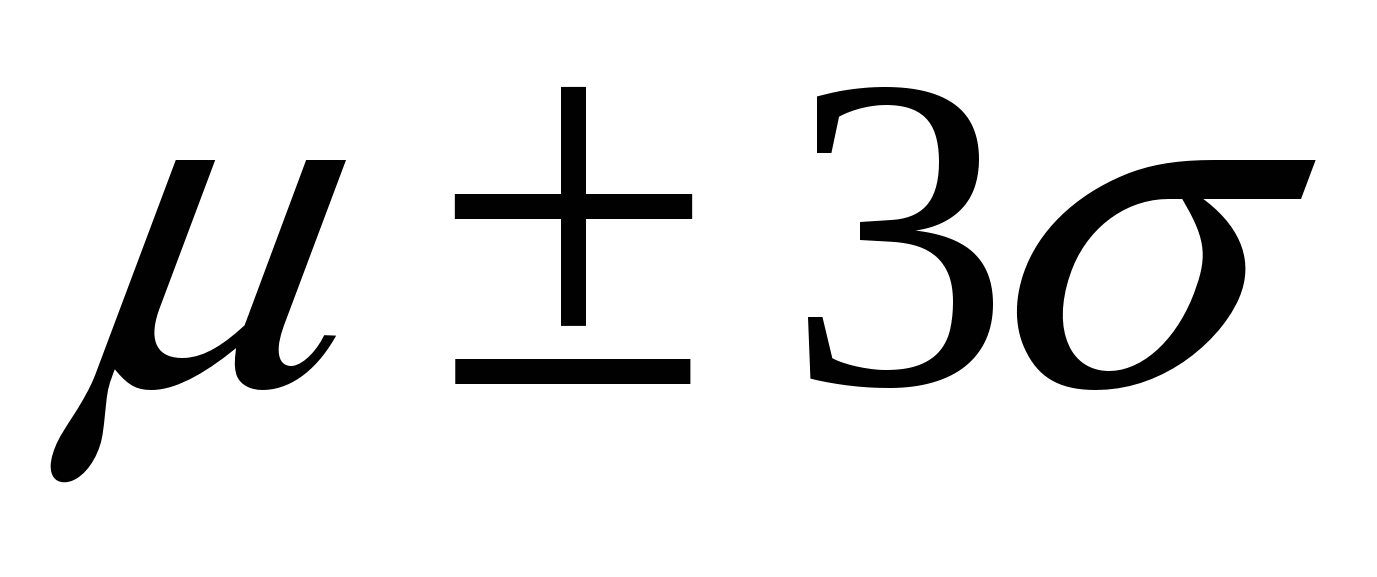 интеграл равен практически всей площади, ограниченной кривой распределения и осью абсцисс (99,7 %). Интеграл (4.2), равный на рис. 4.2 заштрихованной площади, показывает вероятность Р появления результата интеграл равен практически всей площади, ограниченной кривой распределения и осью абсцисс (99,7 %). Интеграл (4.2), равный на рис. 4.2 заштрихованной площади, показывает вероятность Р появления результата 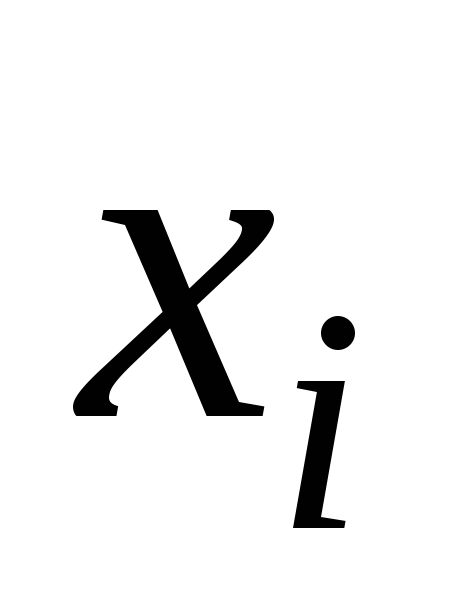 в указанной области значений в указанной области значений 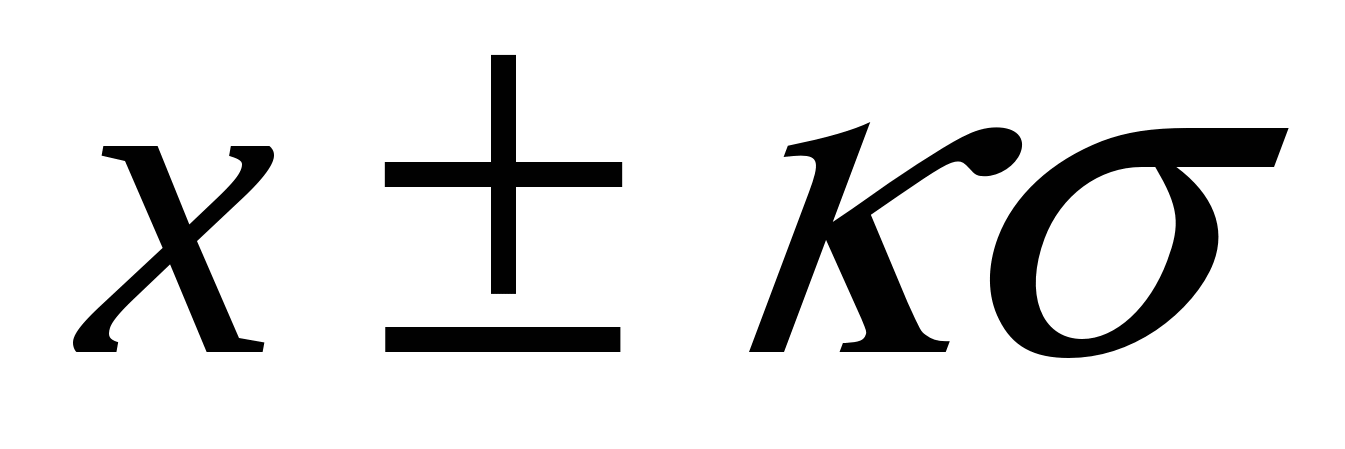 (от (от 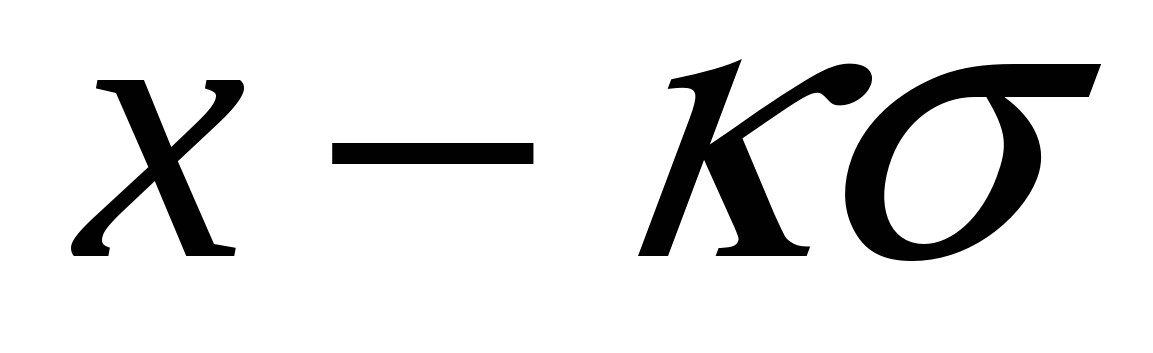 до до 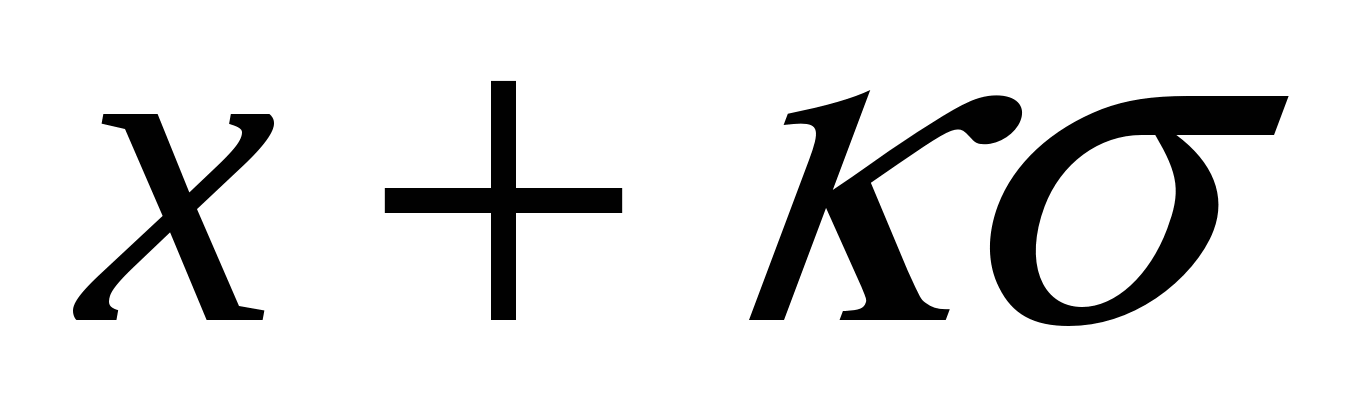 ). Эту величину вероятности называют доверительной вероятностьюили статистической надежностью, интервал от ). Эту величину вероятности называют доверительной вероятностьюили статистической надежностью, интервал от 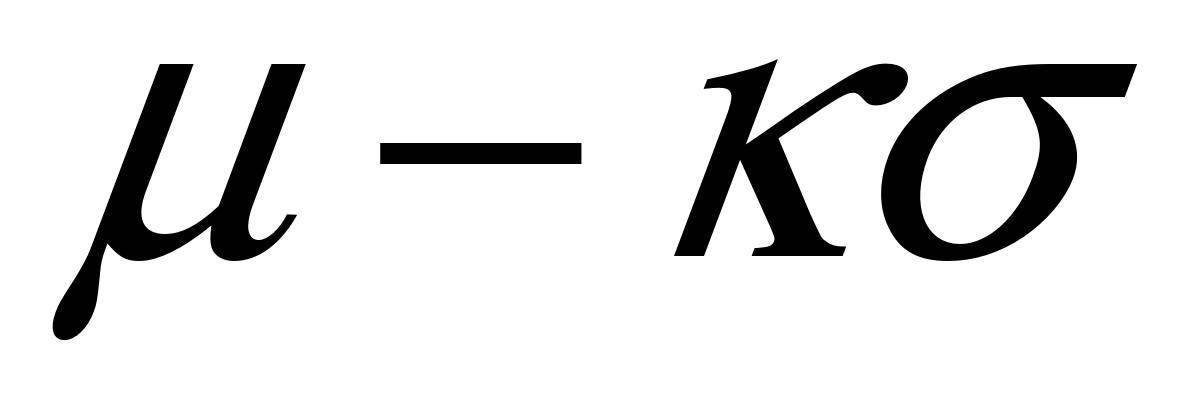 до до 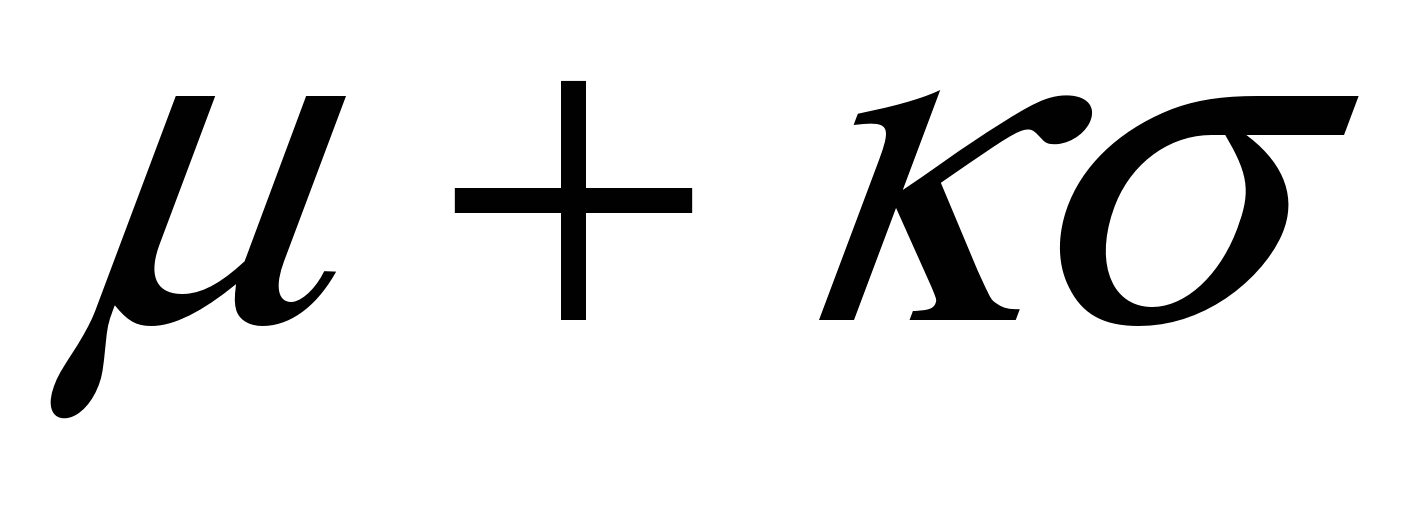 – доверительным интервалом, а границы интервала – доверительными границами. – доверительным интервалом, а границы интервала – доверительными границами.
а
б
в
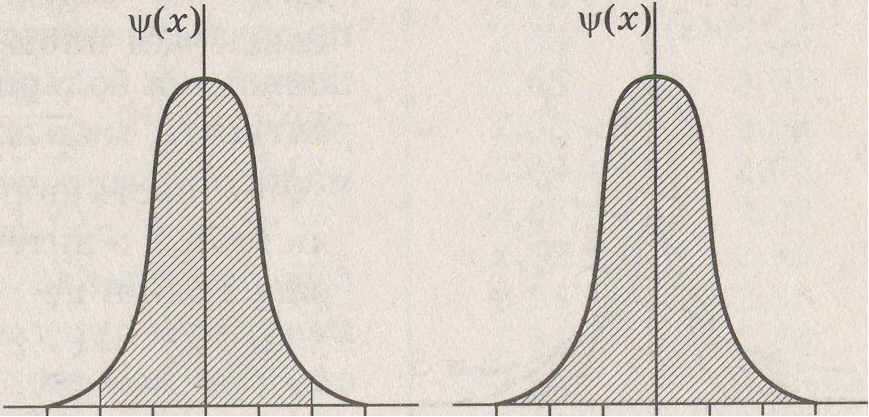
Рис. 4.2. Интегрирование уравнения Гаусса в пределах:
а – 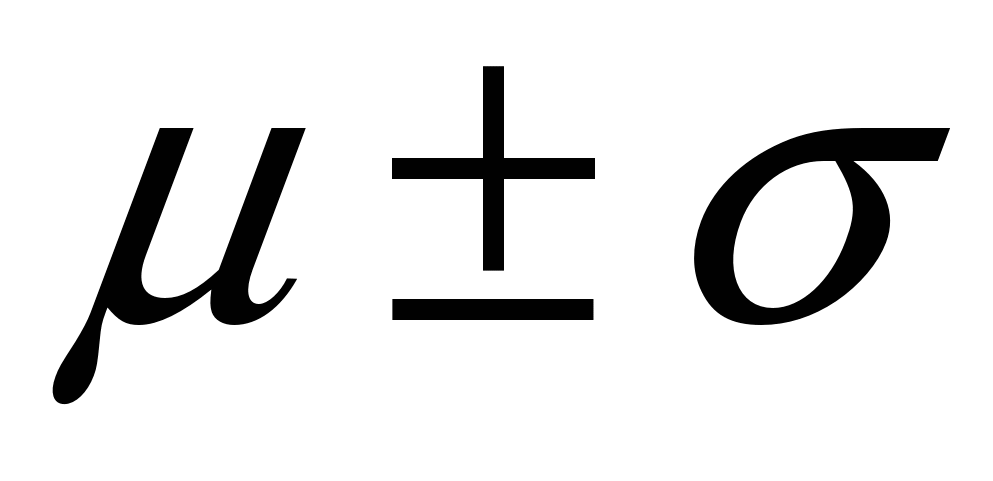 (68,3 %); б – (68,3 %); б – 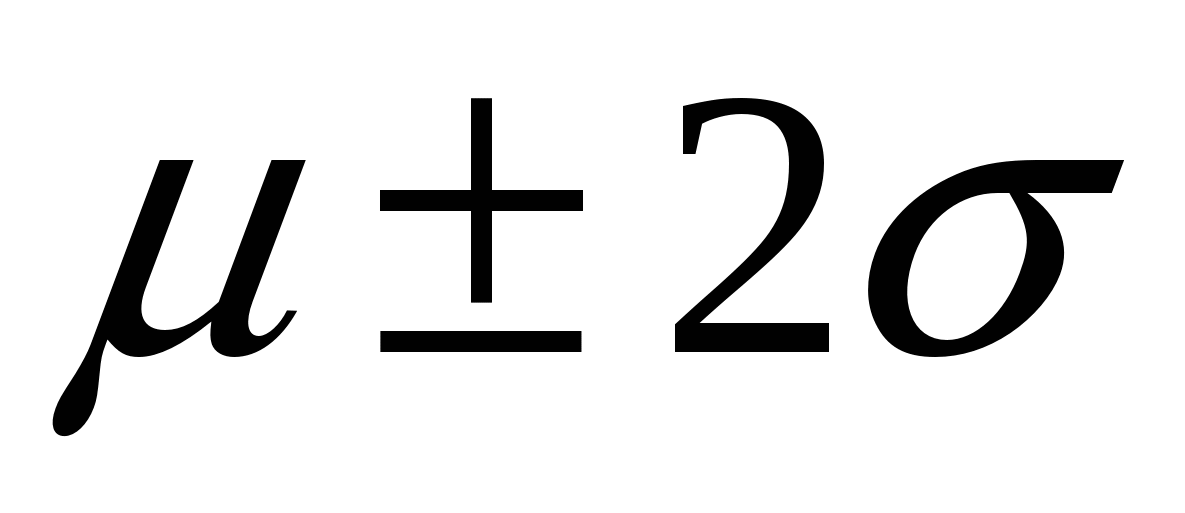 (95,0 %); в – (95,0 %); в – 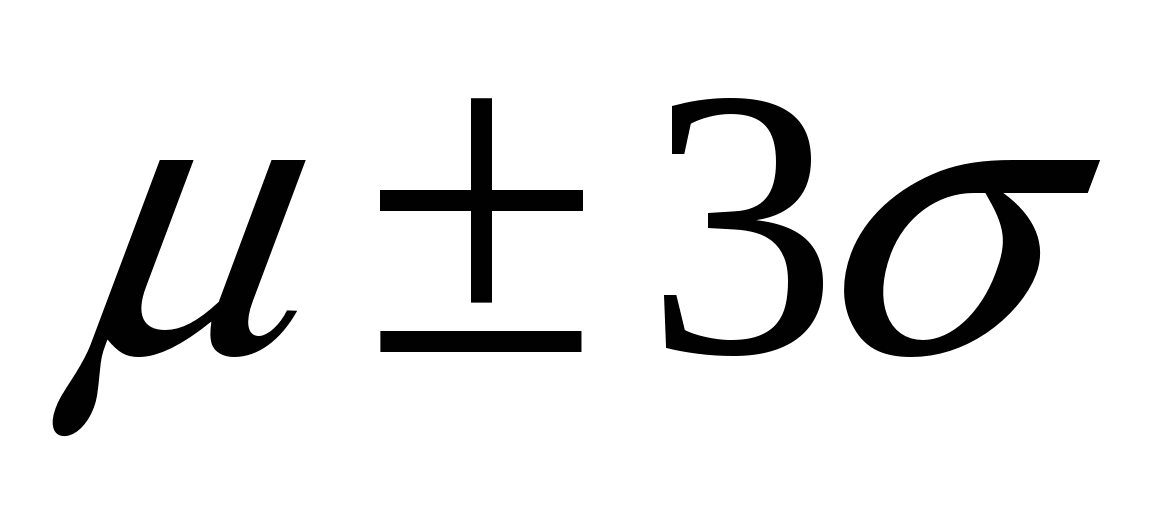 (99,7 %) (99,7 %)
Таким образом, можно сказать, что доверительная вероятность получения результата в пределах от 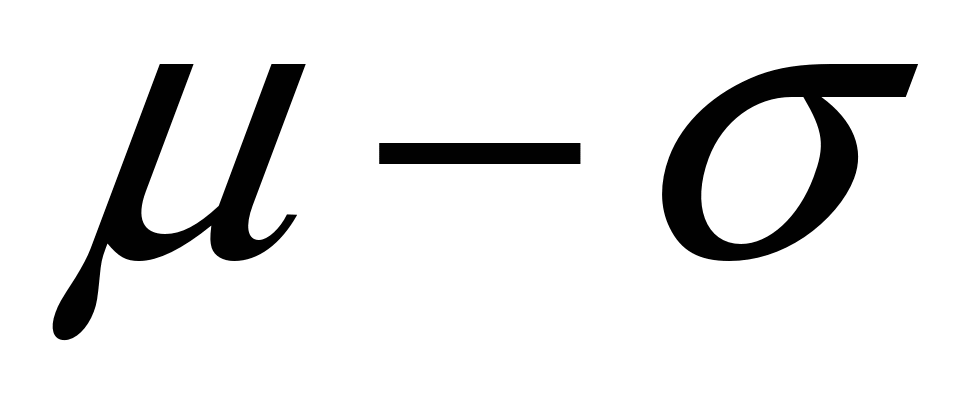 до до 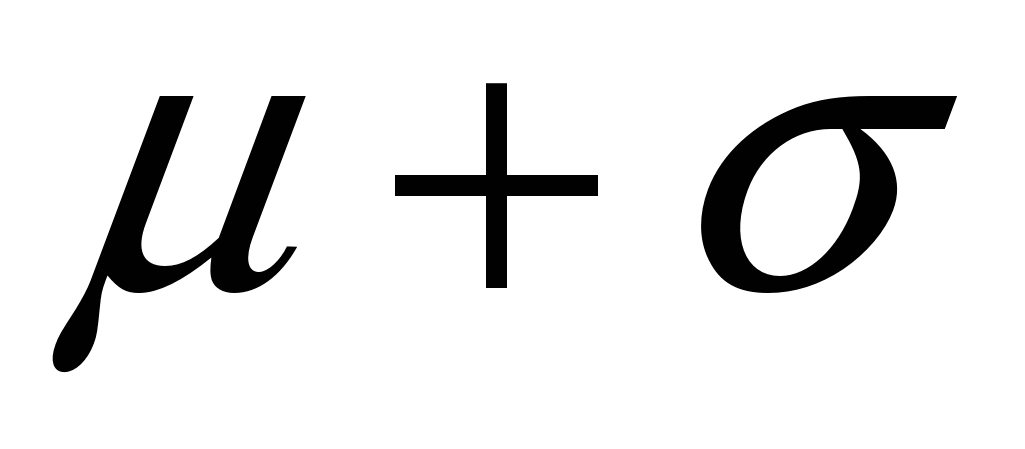 составляет 68,3 %, т.е. в этих пределах лежит 2/3 всех результатов. Внутри пределов составляет 68,3 %, т.е. в этих пределах лежит 2/3 всех результатов. Внутри пределов 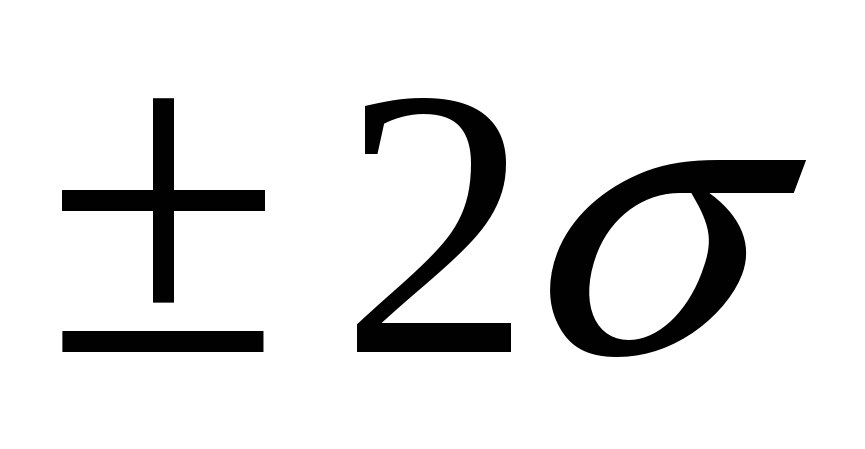 будет находиться 95 % всех значений, а диапазон в будет находиться 95 % всех значений, а диапазон в 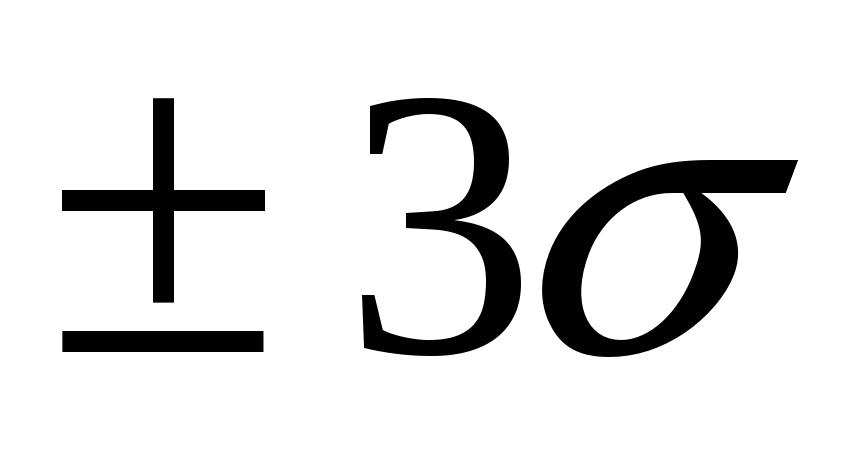 охватывает 99,7 %, т.е. практически все значения. Вероятность получения результата анализа, который будет находиться вне пределов интегрирования, равна α: охватывает 99,7 %, т.е. практически все значения. Вероятность получения результата анализа, который будет находиться вне пределов интегрирования, равна α:
α = 1 – Р
Эту величину называют уровнем значимости.
Классическая теория погрешностей, основанная на нормальном распределении, нашла широкое применение в астрономии, геодезии и других областях, где выполняется большое число измерений одной величины. Однако при обработке данных по анализу вещества она оказалась недостаточно эффективной, так как обычно приводила к заниженным, слишком оптимистичным значениям погрешности. Действительно, в соответствии с законом нормального распределения вероятность появления малых погрешностей значительно больше, чем вероятность появления больших, поэтому при небольшом числе наблюдений (параллельных проб) большие погрешности обычно не появляются, что и приводит к занижению погрешности, если небольшое число результатов обрабатывать в соответствии с нормальным распределением. Более корректная величина погрешности получается при использовании статистики малых выборок, развивающейся с начала ХХ в. (t-pacпределение, так называемое распределение Стьюдента и др.).



|
 Скачать 0.91 Mb.
Скачать 0.91 Mb.