Курсовая матрицы. Иван Орлов Матрицы. Министерство образования Московской области Государственное бюджетное профессиональное образовательное учреждение Колледж Подмосковье проект

• Название: Министерство образования Московской области Государственное бюджетное профессиональное образовательное учреждение Колледж Подмосковье проект
• Анкор: Курсовая матрицы
• Дата: 11.06.2021
• Размер: 87.35 Kb.
• Имя файла: Иван Орлов Матрицы.docx
• Тип: Реферат; #216852

Министерство образования Московской области

Государственное бюджетное профессиональное образовательное учреждение «Колледж «Подмосковье»

ПРОЕКТ

Матрицы: определение, практическое применение.

Выполнил: студент группы ТМП-10.6

Орлов Иван Витальевич

Руководитель: преподаватель математики

Пономаренко Татьяна Ивановна

Химки, 2021
СОДЕРЖАНИЕ

СОДЕРЖАНИЕ 2

Введение 2

История 3

1. Теоретическая часть 5

1. 1 Определение 5

1.2. Обозначения 6

2. Практическая часть 8

2.1. Транспонированная матрица 8

2.2. Вектор-строка и вектор-столбец 8

2.3. Операции над матрицами 8

2.4. Линейные комбинации 10

2.5. Линейная зависимость 10

2.6. Ранг матрицы 11

3. Примеры 13

3.1. Матрица как запись коэффициентов системы линейных уравнений 13

3.2. Квадратная матрица и смежные определения 14

Заключение 15

Список используемой литературы 16

Введение

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы допускают следующие алгебраические операции:

• 
  сложение матриц, имеющих один и тот же размер;
  
• 
  умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);
  
• 
  умножение матрицы на элемент основного кольца или поля (т. н. скаляр).
  

Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.

Матрица представляет собой матрицу некоторого линейного оператора: свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.

В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.
История

Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
1. Теоретическая часть
1. 1 Определение

Пусть   и  , где  , — два конечных множества.

Назовём матрицей размера   (читается m на n) с элементами из некоторого кольца или поля   отображение вида

.

Если индекс i пробегает множество M, а j пробегает множество N, то элемент A(i,j) оказывается элементом матрицы, находящемся на пересечении i-той строки и j-ого столбца:

• 
  i-ая строка матрицы состоит из элементов вида A(i,j), где j пробегает всё множество N;
  
• 
  j-ый столбец матрицы состоит из элементов вида A(i,j), где i пробегает всё множество M.
  

Таким образом, матрица размера   состоит в точности из

• 
  m строк (по n элементов в каждом)
  
• 
  и n столбцов (по m элементов в каждом).
  

В соответствии с этим

• 
  каждую строку матрицы можно интерпретировать как вектор в n-мерном координатном пространстве  ;
  
• 
  каждый столбец матрицы — как вектор в m-мерном координатном пространстве  .
  

Сама матрица естественным образом интерпретируется как вектор в пространстве   имеющим размерность mn. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); то что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.

Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размером квадратной матрицы или её порядком.
1.2. Обозначения

Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть

,

тогда A — матрица, которая интерпретируется как прямоугольный массив элементов поля   вида a_ij = A(i,j), где

• 
  первый индекс означает индекс строки:  ;
  
• 
  второй индекс означает индекс столбца:  ;
  

таким образом, a_ij — элемент матрицы A, находящийся на пересечении i-той строки и j-того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера  :



или просто:

A = (a_ij),

если нужно просто указать обозначение для элементов матрицы.

Иногда, вместо a_ij, пишут a_i,j, чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.

Если необходимо дать развёрнутое представление матрицы в виде таблицы, то используют запись вида



Можно встретить как обозначения с круглыми скобками «(…)», так и обозначения с квадратными скобками «[…]». Реже можно встретить обозначения с двойными прямыми линиями "||…||").

Поскольку матрица состоит из строк и столбцов, для них используются следующие обозначения: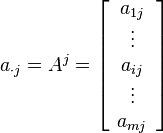

 — это i-тая строка матрицы A.

 — это j-тый столбец матрицы A.

Таким образом, матрица обладает свойственным представлением — по столбцам:



и по строкам: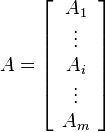

.

Такое представление позволяет формулировать свойства матриц в терминах строк или в терминах столбцов.







































2. Практическая часть

2.1. Транспонированная матрица

С каждой матрицей A = (a_ij) размера   связана матрица B = (b_ij) размера   вида



Такая матрица называется транспонированной матрицей для A и обозначается так A^T. Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица A = (a_ij) размера   при этом преобразовании станет матрицей размерностью   .
2.2. Вектор-строка и вектор-столбец

Матрицы размера   и   являются элементами пространств   и   соответственно:

• 
  матрица размера   называется вектор-столбцом и имеет специальное обозначение:
  

• 
  матрица размера   называется вектор-строкой и имеет специальное обозначение:
  

2.3. Операции над матрицами

Умножение матрицы на число

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен



Сложение матриц

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен



Умножение матриц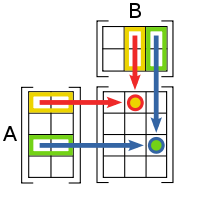



Умножение матриц (обозначение: AB, реже со знаком умножения  ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.



Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность  , B —  , то размерность их произведения AB = C есть  .

Комплексное сопряжение

Если элементами матрицы A = (a_ij) являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна  . Здесь   — число, комплексно сопряжённое к a.

Транспонирование и эрмитово сопряжение

Транспонирование уже обсуждалось выше: если A = (a_ij), то A^T = (a_ji). Для комплексных матриц более употребительно эрмитово сопряжение:  . С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряжённая матрица — это матрицы оператора, сопряжённого относительно скалярного или эрмитова произведения, соответственно.

Взятие определителя или перманента
2.4. Линейные комбинации

В векторном пространстве линейной комбинацией векторов   называется вектор



где   — коэффициенты разложения:

• 
  если все коэффициенты равны нулю, то такая комбинация называется тривиальной,
  
• 
  если же хотя бы один коэффициент отличен от нуля, то такая комбинация называется нетривиальной.
  

Это позволяет описать произведение C = AB матриц A и B терминах линейных комбинаций:

• 
  столбцы матрицы C — это линейные комбинации столбцов матрицы A с коэффициентами, взятыми из матрицы B;
  
• 
  строки матрицы C — это линейные комбинации строк матрицы B с коэффициентами, взятыми из матрицы A.
  

2.5. Линейная зависимость

Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.

Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или



где не все числа   равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.

Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.

Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:

• 
  если строки матрицы C линейно зависят от строк матрицы B, то C = AB для некоторой матрицы A;
  
• 
  если столбцы матрицы C линейно зависят от столбцов другой матрицы A, то C = AB для некоторой матрицы B.
  

2.6. Ранг матрицы

Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.

Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.

2.7. Матричные операции

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Возводить в степень можно только квадратные матрицы.

• 
  Ассоциативность сложения: A + (B + C) = (A + B) + C.
  
• 
  Коммутативность сложения: A + B = B + A.
  
• 
  Ассоциативность умножения: A(BC) = (AB)C.
  
• 
  Вообще говоря, умножение матриц некоммутативно:  . Используя это свойство, вводят коммутатор матриц.
  
• 
  Дистрибутивность умножения относительно сложения:
  

A(B + C) = AB + AC;

(B + C)A = BA + CA.

• 
  С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
  
• 
  Свойства операции транспонирования матриц:
  

(A^T)^T = A

(AB)^T = B^TA^T

(A ^{− 1})^T = (A^T) ^{− 1}, если обратная матрица A ^{- 1} существует.

(A + B)^T = A^T + B^T

detA = detA^T
3. Примеры
3.1. Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными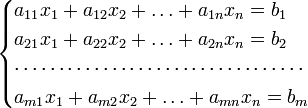



можно представить в матричном виде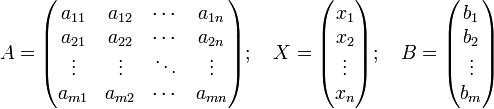



и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{- 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{- 1}AX = A ^{- 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{- 1}B.

Все правила, по которым проводятся операции над матрицами, выводятся из операций над системами уравнений.
3.2. Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю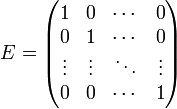



Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{- 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности   на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.
Заключение

В моей работе я доказал, что матрицы могут быть применимы в обыденной жизни. Например, при решении задач о количестве учеников в классе, при строительстве сооружений, в экономике, при подсчете количества выпущенной продукции, и её цены.
Так же в моей работе присутствует теория о матрицах, правилах действий над ними, изложенная в доступной форме, примеры решения систем уравнений с помощью определителей и т.д.
Я убедился, что любую реальную ситуацию можно представить в виде математической модели, а затем найти её решения.










Список используемой литературы

1. 
   Дж. Голуб, Ч.Ван Лоун Матричные вычисления. — М.: Мир, 1999.
   
2. 
   Беллман Р. Введение в теорию матриц - eqworld.ipmnet.ru/ru/library/books/Bellman1969ru.djvu. — М.: Мир, 1969 \.
   
3. 
   Гантмахер Ф. Р. Теория матриц (2-е издание) - eqworld.ipmnet.ru/ru/library/books/Gantmaxer_matric_1966ru.djvu. — М.: Наука, 1966
   
4. 
   Ланкастер П. Теория матриц - eqworld.ipmnet.ru/ru/library/books/Lankaster1973ru.djvu. — М.: Наука, 1973
   
5. 
   Соколов Н. П. Пространственные матрицы и их приложения - eqworld.ipmnet.ru/ru/library/books/Sokolov1960ru.djvu. — М.: ГИФМЛ, 1960
   
6. 
   Халмош П. Конечномерные векторные пространства = Finite-dimensional vector spaces. — М.: Физматгиз, 1963. — 264 с.