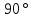Краткий сборник материалов при подготовке к ОГЭ по математике. Конспект к ОГЭ математика. Множества Натуральные
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
Операции над векторами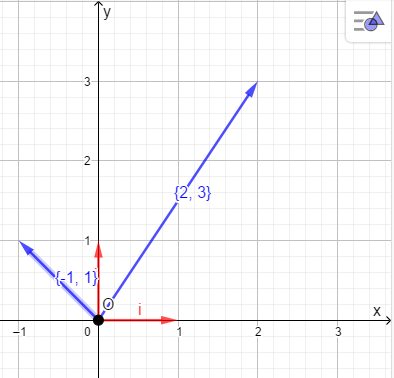 Так как это те же матрицы, то можно просто складывать, вычитать и умножать их координаты: Так как это те же матрицы, то можно просто складывать, вычитать и умножать их координаты: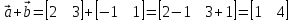 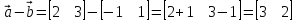 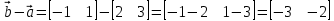 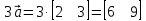 Произведение чуть сложней, мы же говорили, что число строк соответствует числу столбцов. Так вот формально один из векторов мы транспонируем (переворачиваем), и после этого умножаем. Однако можно заметить, что всегда получиться матрица 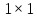 , а значит, произведение векторов всегда даёт просто число! , а значит, произведение векторов всегда даёт просто число!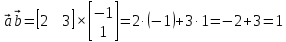 Итог: 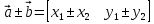 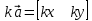 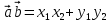 Геометрический способСложениеРисуем два вектора из одной точки, строим параллелограмм и проводим диагональ, диагональ, заключённая между векторами и есть ответ 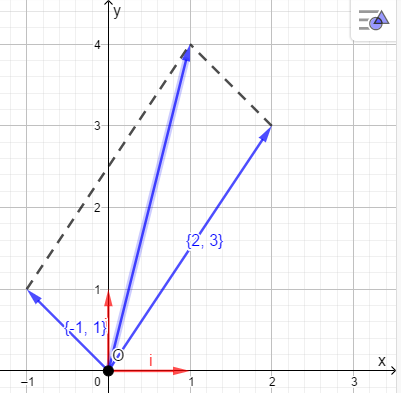 Альтернативный способ, это последовательное построение векторов. То есть там, где заканчивается один, начинается второй и так складываем всё. Итогом будет вектор, проведенный от начала «паровозика» к его концу. 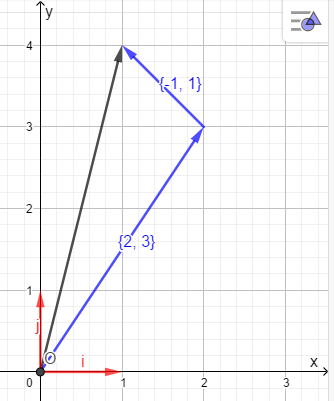 ВычитаниеСтроим вектора из одной точки и соединяем их концы. Направление ставим к тому концу вектора, из которого вычитаем 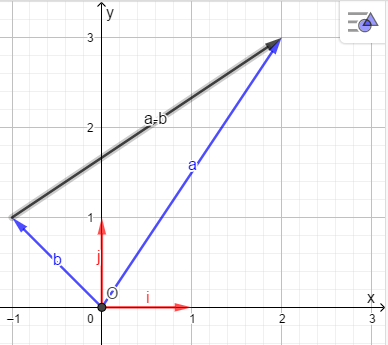 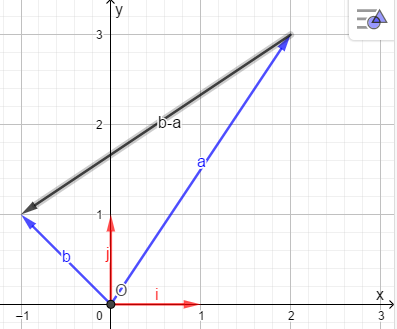 Скалярное произведение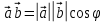 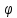 – острый угол между векторами – острый угол между векторамиРасстояние между двумя точками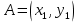 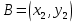 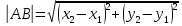 Геометрия Углы
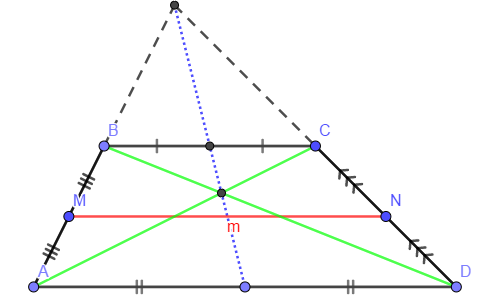
При параллельных прямыхН 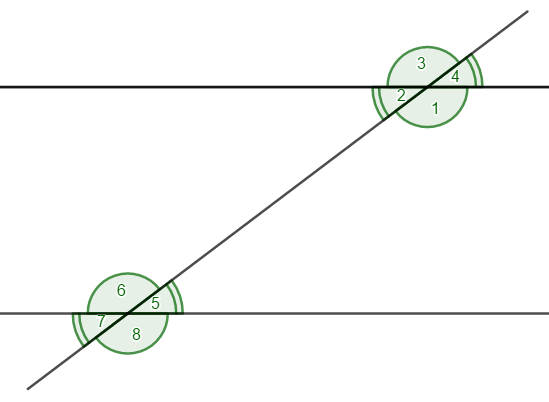 акрестлежащие: акрестлежащие: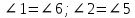 Соответственные: 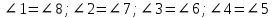 Односторонние: 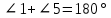 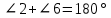 Теорема Фалеса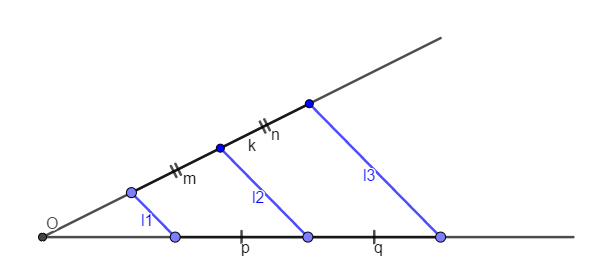 Если параллельные прямые отсекают на одной стороне угла равные отрезки, то и на второй стороне угла, также будут отсечены одинаковые 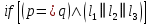  ТреугольникиПроизвольные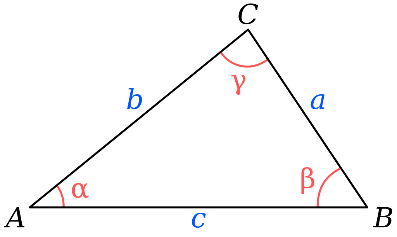 Общие свойства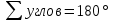 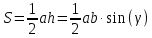 Признаки равенства:Две стороны и угол между ними Сторона и углы при основании Все стороны 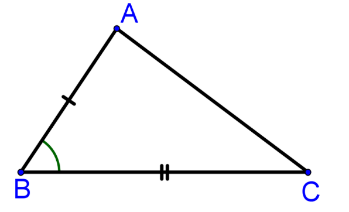 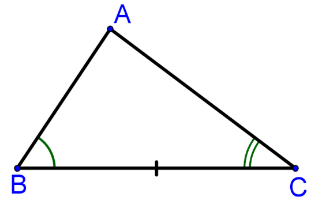 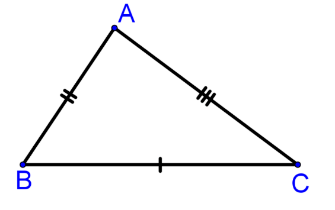 Признаки подобия:Два угла Две пропорциональных стороны и угол между ними Три пропорциональных стороны 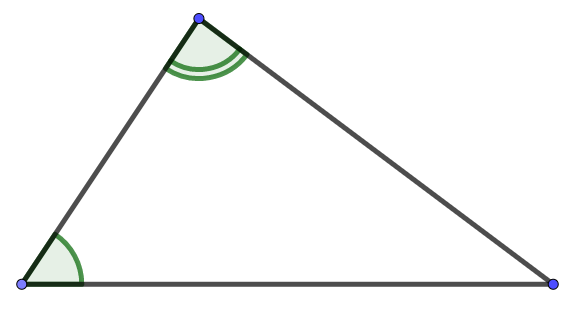 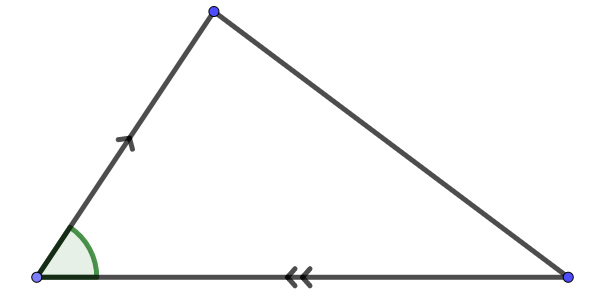 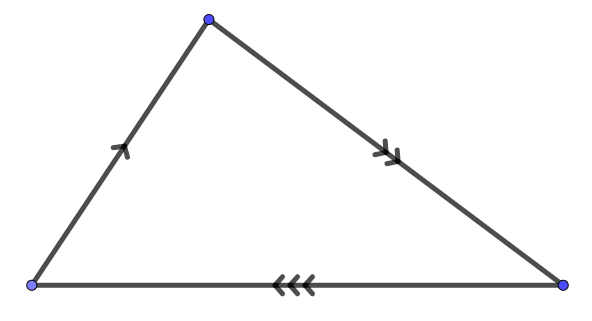 Медиана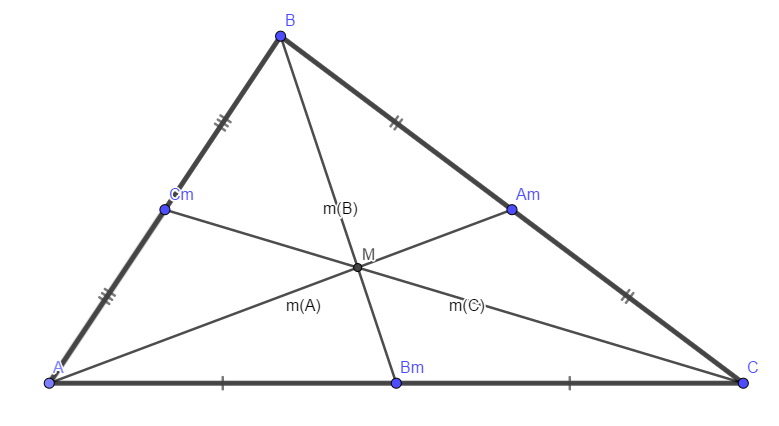 Точка пересечения медиан 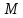 – центр тяжести – центр тяжестиВ точке пересечения медиана делиться на отрезки 2:1 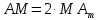 Треугольники образованные медианной имеют одинаковую площадь 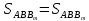 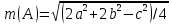 Биссектриса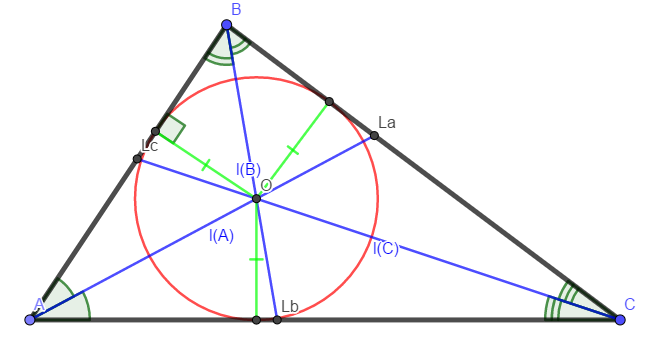 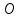 – пересечение биссектрис, центр вписанной окружности – пересечение биссектрис, центр вписанной окружностиБиссектриса равноудалена от сторон, образующие угол Пропорционально делит сторону: 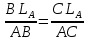 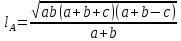 Перпендикуляры и Высоты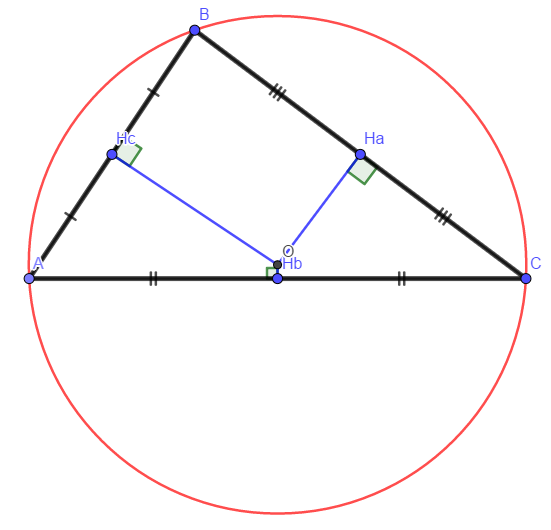 Точка пересечения срединных перпендикуляров является центром описанной окружности Точка пересечения срединных перпендикуляров является центром описанной окружностиВысоты также пересекаются в одной точке, но в отличии от медианы и биссектрис, точка пересечения может находиться вне треугольника 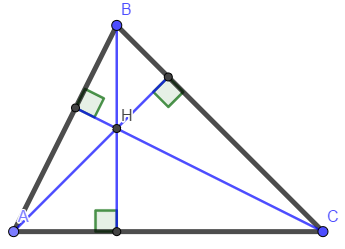 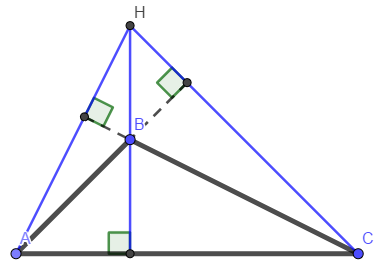 Вписанная, описанная окружность и связь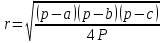 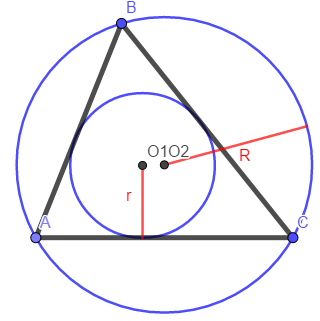 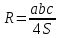 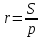 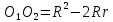 Теорема синусов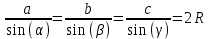 Теорема косинусов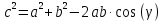 Средняя линия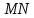 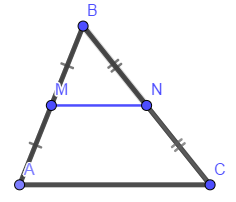 – средняя линия – средняя линия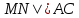 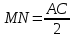 РавнобедренныеБ 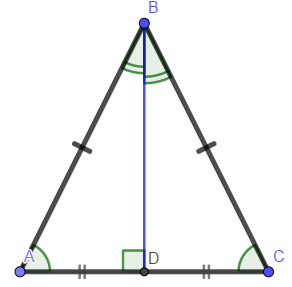 оковые стороны равны оковые стороны равныУглы при основании равны Биссектриса является и медианной, и высотой Равносторонний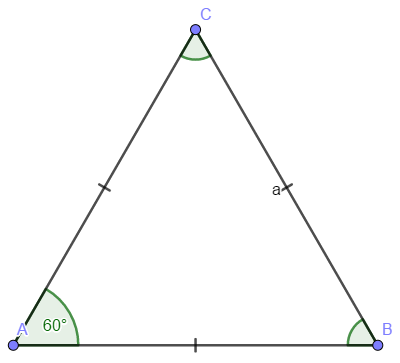 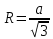 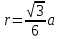 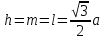 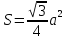 Прямоугольный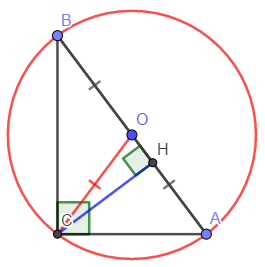 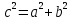 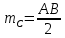 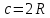 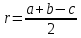 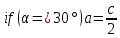 Проекции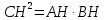 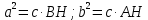 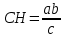 Тригонометрия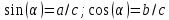 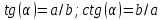 Четырёхугольники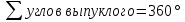 Параллелограмм Вариньона: если у любого четырёхугольника соединить все середины сторон, получиться параллелограмм.
ПаралелаграммС |
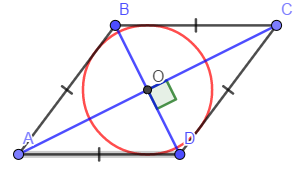
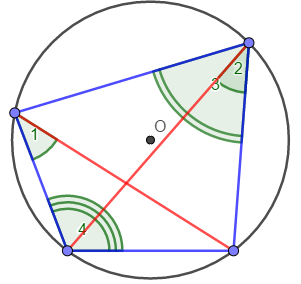 Если в четырёхугольнике, углы, опирающиеся на одну сторону равны ( 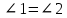 ), то он вписан ), то он вписанЕсли в четырёхугольнике противоположные углы в сумме дают 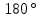 , то он вписан. ( , то он вписан. (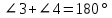 ) ) | 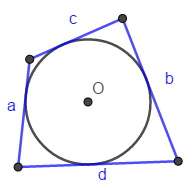 Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны. Верно и обратное. 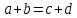 |
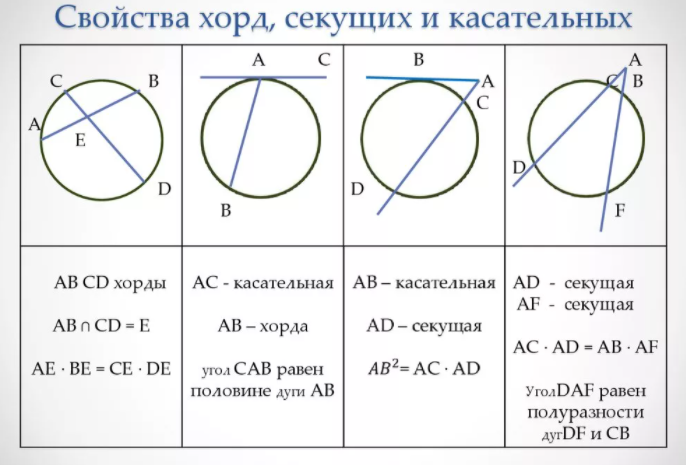
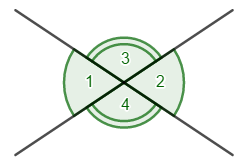
Хорды
Многоугольники
Выпуклые: нет углов больше
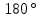
Невыпуклые
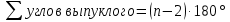
Правильный тот многоугольник, у которого все стороны и углы равны
Стереометрия
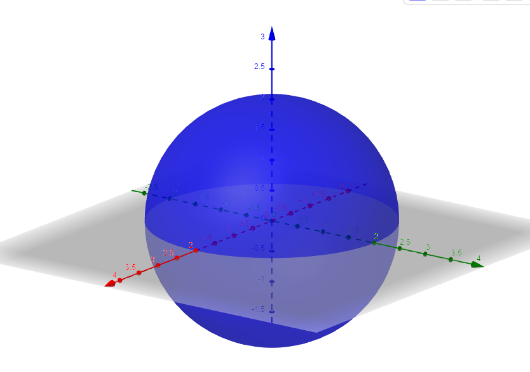 Шар
Шар
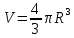
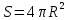
Конус / любая пирамида
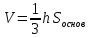
Остальное
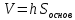


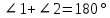
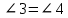
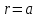
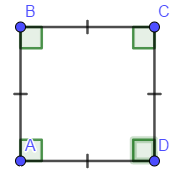
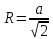
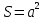
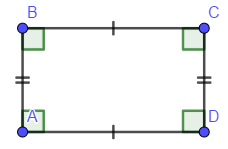
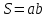
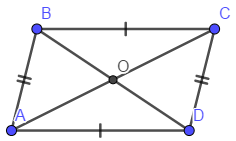 войства:
войства: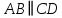
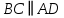
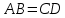
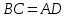
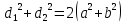
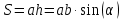
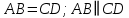
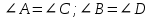
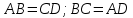
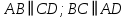
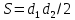
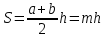
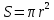
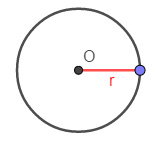
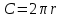
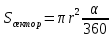
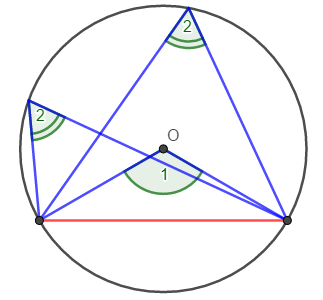
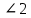 равны, так как опираются на одну хорду.
равны, так как опираются на одну хорду.