Краткий сборник материалов при подготовке к ОГЭ по математике. Конспект к ОГЭ математика. Множества Натуральные
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
Комбинаторика и теория вероятностиСчитается, что этой науки обучить невозможно, её надо просто понять. Вероятность выражается в долях 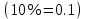 . Для её вычисления требуется разделить интересуемое число вариантов на общее возможное. В этом вся теория вероятности. . Для её вычисления требуется разделить интересуемое число вариантов на общее возможное. В этом вся теория вероятности. А вот для вычисление сколько же этих вариантов, а помощь приходит комбинаторика. Здесь основное правило: «Если говоришь «и» – умножай, если «или» – складывай». Рассмотрим примеры: Простая часть: Какова вероятность, что выпадет орёл при подбрасывании монетки? — нас интересует один вариант – орёл. Всего два: орёл и решка. Делим, получаем ответ 0.5 В игре монополия игроку нужно выпадение числа больше 4 (не включая, игра с одним кубиком), каков шанс его удачи? — Числа больше четырёх: 5 и 6. Всего возможных чисел 6. Делим 2 нужных на 6 возможных. Ответ: 0.33 Средняя часть: Каков шанс того, что азартный человек вытянет подряд два туза из покерной колоды? —Рассмотрим задачу внимательнее и представим ситуации. Человек тянет из колоды карту, она должна быть тузом, и потом опять тянет карту в надежде, что та тоже будет тузом. Заметим, что встретилась та «И», значит придётся перемножать вероятность каждого события. Событие 1: человек первый раз достаёт туза. Вероятность 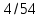 Событие 2: человек достаёт второго туза, но в колоде уже осталось три туза, да и сама колода уже на одну карту меньше, следовательно вероятность уже не 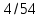 , а , а 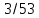 Перемножаем, получаем ответ 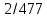 В монополии после трёх дублей игрок идёт в тюрьму, какова вероятность в неё попасть? – Опять вникаем! Он должен кинуть три раза кубики, значит придётся перемножить вероятность трёх случаев. Вероятность случая: тут надо понять, что не стоит перемножать сразу 1/6 на 1/6. Нет. Первый кубик, может лечь любой цифрой, главное, чтобы второй лег той же, а значит вероятность всего события определится вероятностью второго кубика. А то, что он выпадет нужной нам стороной – 1/6. Во всех ситуациях всё повторяется, то есть все три случая имеют одну вероятность Перемножаем и получаем ответ: 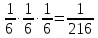 Сложная часть: На столе 10 карточек на каждой своя цифра, лежат рубашкой вверх, то есть цифр не видно. Человек берет три карточки и кладёт в любой угодной ему последовательности. После открывает карточки и смотрит получившееся число (если число начинается с нуля – ничего страшного, его не считают, смотрят последние две цифры). Какова вероятность что оно чётное. — Как считать личное дело каждого, бывает разный ход мыли и разные методы. Я предлагаю следующий способ. После вытягивания трёх карточек возможны четыре случая: ЧЧЧ, НЧЧ, ННЧ, ННН (Н-нечетное число на карточке, Ч-четное). Найдём вероятность каждого случая, а потом, отдельно, какова же вероятность выпадения четного числа в этом случае. Начнём с ЧЧЧ. Из 10 цифр нужно вытянуть сразу 3 чётных. Вытягиваем первую четную карточку – вероятность 5/10, вторую – 4/9 и третью – 3/8. Перемножаем. Вероятность, что мы вытащим сразу три чётных карточки 1/12. Естественно из всех чётных цифр получится исключительно чётное число, так что итог – 1/12 Дальше НЧЧ. Схема таже: тянемся за нечётной – 5/10, потом ищем чётную – 5/9 и снова чётную – 4/8, итого 5/36. НО! это когда мы вытягивали именно в этой последовательности, а ведь можно вытянуть ЧНЧ или ЧЧН. Вероятность каждого такая же – 5/36. Но все три случая дадут 15/36. Теперь нужно определить вероятность составления четного числа. Главное, чтобы число заканчивалось на чётное. Шанс, что закончится на нечетное 1/3, а вариант, который нас интересует получается 1-1/3=2/3. Итог: 15/36*2/3=5/18 Случай ННЧ. Если посмотреть на предыдущее событие, то они отличаются только одной буквой, по сути они одинаковы – шанс, того что соберется такая комбинации тоже 15/36. А собрать четное число уже сложнее, нужно чтобы четная карточка оказалась в конце, вероятность этого 1/3. Итог: 15/36*1/3=5/36 ННН нас не интересует, из него нельзя сложить четное число Складываем все итоговые вероятности: 1/12+5/18+5/36=1/2 Ответ: 1/2. Векторы и координаты Вектор- наплавленный отрезок, для совершения операций над ним придётся научиться ориентироваться хотя бы в двумерном пространстве. По своей сути, вектор это таже матрица, одномерный массив, в котором содержаться его координаты. Координаты вектора немного отличаются от обычных декартов, здесь принято выражать через оси 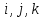 . По сути всё те же . По сути всё те же 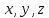 , но декартовая величина задаёт начало отчёта вектора, а саму длину и направление уже определяет вектора , но декартовая величина задаёт начало отчёта вектора, а саму длину и направление уже определяет вектора 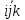 (вот только точка отчета вектора зачастую не используется, записывается просто в векторных координатах, предполагая, что все векторы тянуться из начала координат) (вот только точка отчета вектора зачастую не используется, записывается просто в векторных координатах, предполагая, что все векторы тянуться из начала координат)Как итог вектора записываются следующим образом: 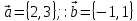 |
