Краткий сборник материалов при подготовке к ОГЭ по математике. Конспект к ОГЭ математика. Множества Натуральные
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
ФункцииЛинейная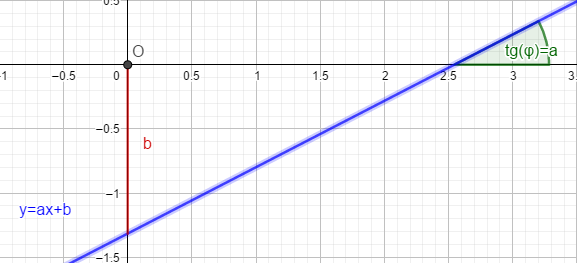 Гипербола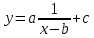 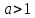 – растягивается – растягивается 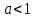 – сужается – сужается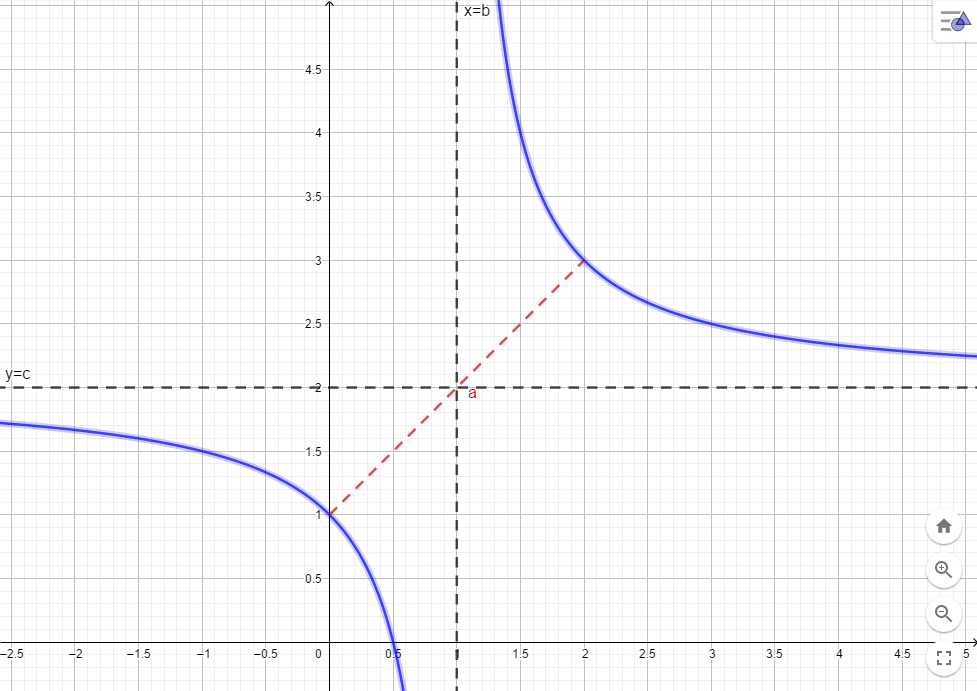 Парабола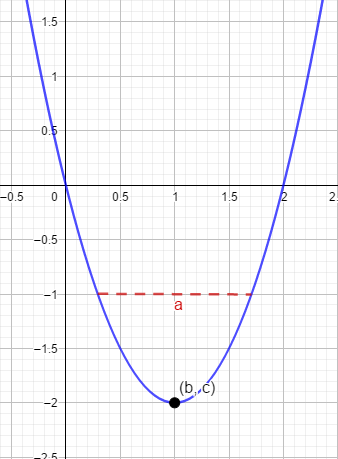 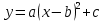 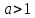 – сужается – сужается 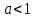 – растягивается – растягивается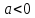 – ветви параболы будут направленны вниз – ветви параболы будут направленны внизОкружность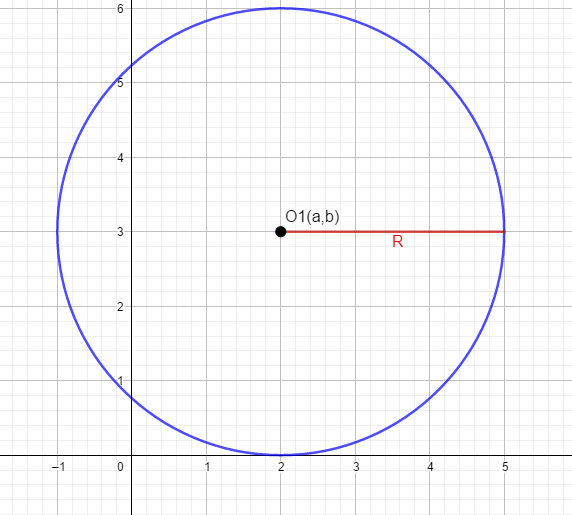 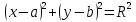 Тригонометрические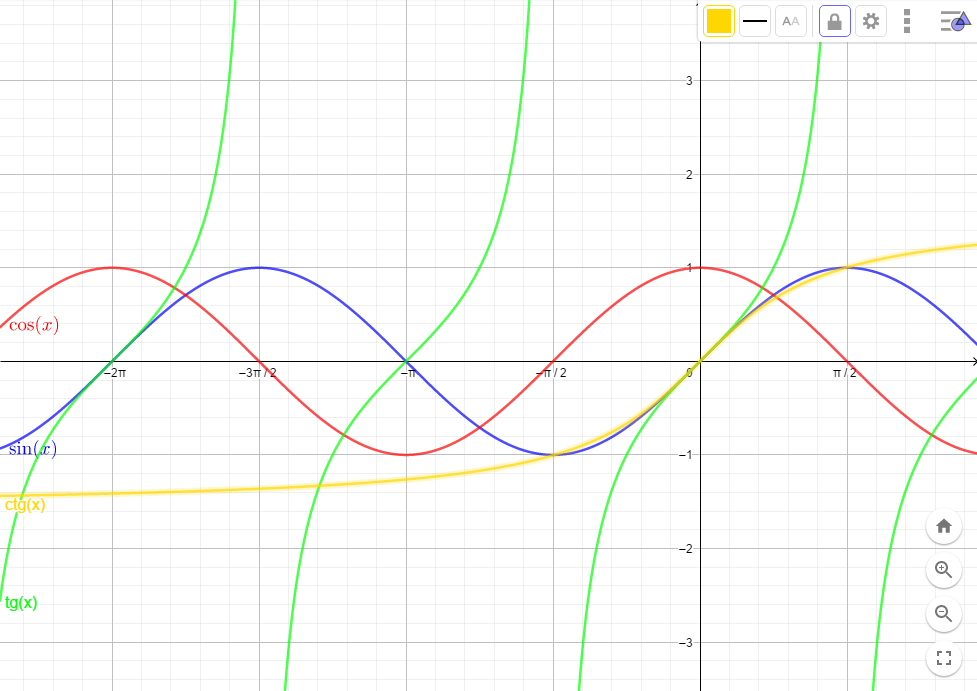 Другие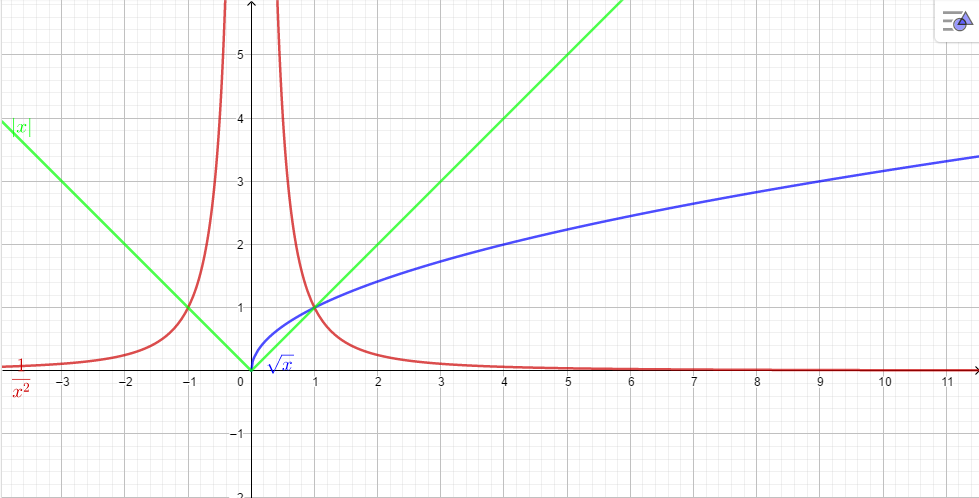 НеравенстваСамое важное привести к каноническому виду: разложить на множители, и в каждом множителе старшая степень должна быть с положительным знаком. Правила: Перенос слагаемых такой же, как и в уравнениях: просто меняем знак у члена При умножении на отрицательное число, меняется и знак неравенства! При сокращении обязательно удостоверится, что множитель не обращается в ноль, чтобы не потерять корень После приведения к каноническому виду, рисуем ось  , отмечаем корни. Если знак неравенства включает нули их принято закрасить, если просто «больше» или «меньше» оставить проколотыми. Теперь рисуем волны и ставим знаки у гребней: тот, что правее всех имеет , отмечаем корни. Если знак неравенства включает нули их принято закрасить, если просто «больше» или «меньше» оставить проколотыми. Теперь рисуем волны и ставим знаки у гребней: тот, что правее всех имеет  ! дальше если множитель, от которого вышел корень, имеет нечетную степень то знак у следующего корня меняется, если степень четная, то знак будет тот же. ! дальше если множитель, от которого вышел корень, имеет нечетную степень то знак у следующего корня меняется, если степень четная, то знак будет тот же.Не забыть область определения, если такая имеется! При записи ответа существует специальные обозначения: «[» или «]» – это включая, в то время как круглые скобки наоборот исключая, «v» – знак, обозначающий «и». Бесконечность – несуществующее число, при записи использовать «(» или «)». Пример: Условие: 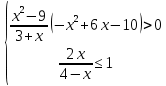 В случаи системы, желательно решить неравенство отдельно друг от друга, а после объединить ответы. Начнём с первого: Необходимо привести к каноническому виду 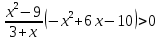 Воспользуемся формулой сокращенного умножения: 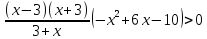 Разложим квадратный множитель. Для начала, заметив у старшей степени минус, вынесем его и сократим, помним, что, меняя знак, меняется и клюв у неравенства. 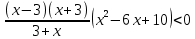 При разложении сталкиваемся с отрицательным дискриминантом, следовательно, корней нет, и этот множитель можно спокойно сократить: 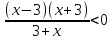 Заметим, что можем сократить 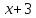 , однако мы должны понимать, что , однако мы должны понимать, что 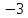 не входит в область допустимых значений: не входит в область допустимых значений: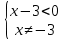 Решаем второе неравенство. Для начала приведём всё к одному знаменателю. 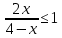 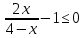 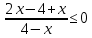 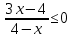 В знаменателе минус. Избавляемся меняя знак неравенства 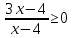 Строим ось и отмечаем все корни и точки. Если не входит в область определения или корень пришёл из знаменателя, то бес сомнений оставляем проколотой. А остальные смотрим на знак неравенства. Рисуем гребни, пусть верхняя сторона будет соответствовать первому неравенству, нижняя – второму. И ставим знаки: правый гребень «+», после меняем в соответствии со степенью.  Определяем какая же область нам нужна. Для первого неравенства меньше нуля, для второго больше  Область где пересекается и верхняя и нижняя часть одновременно и будет ответом.  Ответ: 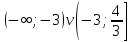 |
