математические методы и модели анализа и прогнозирования развити. Модели прогнозирования экономических процессов Трендовые модели на основе кривых роста
 Скачать 300.97 Kb. Скачать 300.97 Kb.
|
|
2.4. Методы анализа временных рядов. В ПРИМЕРАХ, КОТОРЫЕ БУДУТ РАССМОТРЕНЫ НИЖЕ, ТРЕНД ЯВЛЯЕТСЯ ЛИНЕЙНЫМ. Это означает, что модель тренда легко построить, используя для расчета параметров прямой, наилучшим образом аппроксимирующий данный тренд, метод регрессии. Затем данная модель может использоваться для прогнозирования будущих значений тренда. В действительности, тренд в чистом виде либо не существует, например, при колебании значений спроса вокруг некоторой фиксированной величины, либо в большинстве случаев он является нелинейным. При рассмотрении того, как работают эти методы, мы будем пользоваться одним и тем же моментным временным рядом. ПРИМЕР 1. Предположим, что объемы продаж товара в течение недели описываются следующим временным рядом (рис. 9).
Рис. 9. Моментный временной ряд. Этот временной ряд можно задать в более формализованном виде (рис. 10).
Рис. 10. Моментный временной ряд. 1) Метод подвижного (скользящего) среднего. Метод простого скользящего среднего (simple moving average) состоит в том, что расчет показателя на прогнозируемый момент времени строится путем усреднения значений этого показателя за несколько предшествующих моментов времени. Практически во всех применяемых в настоящее время методах прогнозирования коэффициенты моделей сначала определяются путем подгонки модели к некоторым данным предыстории, а затем проверяются и уточняются по мере поступления новых данных. В методе простого скользящего среднего первоначальные значения элементов ряда заменяются средним арифметическим значением внутри выбранного интервала. Полученное значение относится к середине выбранного интервала. Затем интервал сдвигается на одно наблюдение и расчет скользящего среднего повторяется. Интервалы определения скользящего среднего берутся все время одинаковыми. Чем шире интервал, тем более плавным получается новый ряд. Сглаженный ряд короче первоначального на (N—1) наблюдений, где N — величина интервала сглаживания. Выбор интервала сглаживания определяется конкретной задачей. Если число членов интервала сглаживания нечетное, то полученные значения скользящего среднего приходятся на средний член интервала сглаживания. При четном числе членов интервала сглаживания значения скользящих средних будут располагаться в промежутках между элементами ряда. Обратимся к временному ряду (рис. 10), заданному в примере 1. Для вычисления прогнозируемого объема продаж на четверг поступим следующим образом. Возьмем фактические данные за три предыдущих дня – понедельник, вторник и среду — и найдем их среднее арифметическое: Прогнозируемый объем продаж на пятницу вычисляется аналогичным образом по реальным показателям за три предшествующих дня — вторник, среду и четверг: Подобным же способом рассчитываются прогнозы на субботу, воскресенье и очередной понедельник: И мы получаем следующую таблицу (рис. 11):
Рис. 11. Прогнозирование объема продаж. Сравнительные результаты приведены на рис. 12: сплошными линиями соединены реальные значения, а пунктирными — прогнозируемые. 10 - 8 - 6 - 4 - 2 -
1 2 3 4 5 6 7 8 Рис. 12. Сравнение реальных и прогнозируемых показателей. Для общего случая расчетная формула выглядит так: или 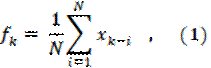 где xk-i — реальное значение показателя в момент времени tk-i, N — число предшествующих моментов времени, используемых при расчете; fk — прогноз на момент времени tk. Замечание. В рассматриваемом примере N = 3. Простота и наглядность — достоинства метода простого скользящего среднего. Но при малом числе наблюдений этот метод приводит к искажению тенденции, величина интервала сглаживания влияет на форму тренда, теряются начальные и конечные элементы ряда. 2) Метод взвешенного подвижного (скользящего) среднего (weighted moving average). При составлении прогноза методом усреднения часто приходится наблюдать, что влияние используемых при расчете реальных показателей оказывается неодинаковым, при этом обычно более свежие данные имеют больший вес. Математически метод взвешенного подвижного среднего можно описать формулой: 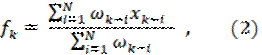 где xk-i — реальное значение показателя в момент времени tk-i, N — число предшествующих моментов времени, используемых при расчете; fk — прогноз на момент времени tk. ωk-i — вес, с которым используется показатель xk-i при расчете. ЗАМЕЧАНИЕ. Вес — это всегда положительное число. В случае, когда все веса одинаковы, мы получаем формулу (1). Для расчетов обратимся к исходному временному ряду, считая, что при составлении прогноза на завтрашний день объем сегодняшних продаж мы возьмем с весом 60, вчерашних — с весом 30, а позавчерашних - с весом 10: ω3 = 60, ω2 = 30, ω1 = 10. Мы имеем: На рисунке 13 дается графическое представление проведенных расчетов: сплошными линиями соединены реальные значения, а пунктирными — прогнозируемые. 10 - - 8 - - 6 - - 4 - - 2 - -
1 2 3 4 5 6 7 8 Рис. 13. Сравнение реальных и прогнозируемых показателей. Для стационарных рядов существует система весовых множителей, позволяющая обеспечить минимальную ошибку прогноза. Эти множители определяются видом автоковариационной функции. Известен метод вычисления таких оптимальных весовых функций для постоянного уровня, тренда и сезонных коэффициентов. В каждом из этих случаев весовые множители экспоненциально уменьшаются по закону αj, а различные значения α, получаемые для уровня, тренда и сезонных коэффициентов, определяются систематическими исследованиями точности прогнозов, получаемых при различных комбинациях весовых функций. Во многих случаях целесообразно использовать последовательность ωj = αj, 0 < α <1, придающую более высокий вес более поздней информации и позволяющую относительно просто оценивать значения коэффициентов даже достаточно сложных моделей, таких, в которых для описания сезонных циклов используются полиномы в сочетании с преобразованиями Фурье (подобное представление можно рассматривать как сложные полиномы). Для модели экспоненциально взвешенного скользящего среднего предложены способы, с помощью которых в те периоды времени, когда средняя ошибка прогноза близка к нулю (благодаря правильности модели и ее коэффициентов), скорость затухания α может быть увеличена; а в те периоды времени, когда средняя ошибка прогноза существенно отличается от нуля и существует опасность того, что модель может «забыть» старую информацию (в этом случае требуется уточнение прогноза), скорость затухания α может быть уменьшена. Уточнение прогноза производится по принципу обратной связи — новые прогнозы корректируются на основе учета ошибок в предшествующих прогнозах. Если при выборе весовых множителей в процессе составления прогноза также используется обратная связь, то не только строгий анализ областей устойчивости данной системы, но и любой анализ вообще становится фактически невозможным. Для анализа эффективности какого-либо метода недостаточно привести примеры, подтверждающие его полезность. Необходимо также выявить области (если они существуют), в которых применение рассматриваемого метода невозможно или неэффективно. 3) Метод экспоненциального сглаживания. 3) При расчете прогноза методом экспоненциального сглаживания (exponential smoothing) учитывается отклонение предыдущего прогноза от реального показателя, а сам расчет проводится по следующей формуле: Где xk-1 — реальное значение показателя в момент времени tk fk — прогноз на момент времени tk; α — постоянная сглаживания. ЗАМЕЧАНИЕ. Значение постоянной α, подчиненной условию 0 < α < 1 , определяет степень сглаживания и обычно выбирается универсальным методом проб и ошибок. Для расчетов вновь обратимся к исходному временному ряду, положив α = 0,2 и считая, что прогноз на понедельник равен 8. Тогда находим Результаты расчетов приведены в таблице (рис. 14):
Рис. 14. Прогнозирование объема продаж. На рисунке 15 дается графическое представление проведенных расчетов (сплошными линиями соединены реальные показатели, пунктирными — прогнозируемые). 10 - - 8 - - 6 - - 4 - - 2 - -
1 2 3 4 5 6 7 8 Рис. 15. Сравнение реальных и прогнозируемых показателей. Метод экспоненциального сглаживания разработан для рядов, состоящих из большого числа наблюдений, при увеличении числа наблюдений точность прогноза должна возрастать. При анализе коротких рядов метод не «срабатывает», так как часто не «успевает» отразить изменения при быстрых темпах роста. Если явление протекает в одних и тех же условиях, то точность прогноза определяется величиной периода предистории явления (базисного периода) и длительности прогнозируемого периода. Количественно это влияние можно оценить по имеющемуся ряду динамики, если одну часть ряда рассматривать как предисторию, а вторую — как прогнозируемую. Получив прогнозирующую функцию по базисному периоду, по второй части ряда можно оценить реальные ошибки прогноза. Изменяя число элементов рядов предистории и прогноза, получим зависимость точности прогноза от периода предистории и величины прогнозируемого периода. ЗАМЕЧАНИЕ. Следует иметь в виду, что при решении реальной задачи прогнозирования временной ряд складывается постепенно и реальное значение показателя на рассчитываемый момент времени нам заранее неизвестно. Прежде чем «заглянуть в будущее» посредством одного из указанных выше методов, обычно проводят расчеты с полным временным рядом, описывающим некоторый промежуток времени в прошлом. Это делается для того, чтобы подобрать подходящее значение N и сравнить результаты прогноза с реальными данными (метод простого скользящего среднего), подобрать подходящие значения N и весов и сравнить результаты прогноза с реальными данными (метод взвешенного скользящего среднего), подобрать подходящие значения постоянной сглаживания α и сравнить результаты прогноза с реальными данными (метод экспоненциального сглаживания). |
