математические методы и модели анализа и прогнозирования развити. Модели прогнозирования экономических процессов Трендовые модели на основе кривых роста
 Скачать 300.97 Kb. Скачать 300.97 Kb.
|
|
4) Метод проецирования тренда. Тренды могут быть описаны различными уравнениями — линейными, логарифмическими, степенными и т. д. Фактический тип тренда устанавливают на основе подбора его функциональной модели статистическими методами либо сглаживанием исходного временного ряда. Выделяют тренды восходящий (бычий), нисходящий (медвежий) и боковой (флэт). На графике часто рисуют линию тренда, которая на восходящем тренде соединяет две или более впадины цены (линия находится под графиком, визуально «поддерживая и подталкивая» график вверх), а на нисходящем тренде соединяет два или более пика цены (линия находится над графиком, визуально «ограничивая и придавливая» график вниз). Трендовые линии являются «линиями поддержки» (для восходящего тренда) или «линиями сопротивления» (для нисходящего тренда). Основной идеей метода проецирования линейного тренда (trend projection) является построение прямой, которая «в среднем» наименее уклоняется от массива точек (ti, xi), i = 1,2,...,n, заданного временным рядом (рис. 16). Эта прямая ищется в следующем виде: x = at + b, (3) где а и b — постоянные, подлежащие определению. x  x=at+b x=at+bxi
x1
t1 t2 ti … tn t Рис. 16. Метод проецирования тренда. Чтобы найти коэффициенты а и b, поступают так: для каждого значения ti; переменной t, пользуясь формулой (3), вычисляют соответствующее значение переменной х, затем находят разность (ati + b – xi), которую затем возводят в квадрат (чтобы не думать о знаке): (ati + b – xi)2 (i =1, …, n) и, складывая, в итоге получают: 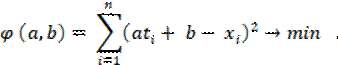 Функция φ (a, b) принимает минимальное значение в том случае, когда величины a и b удовлетворяют следующей линейной системе: 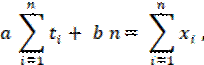 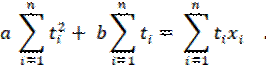 Эта система всегда имеет единственное решение. Рассмотрим конкретный пример, вновь обратившись к заданному временному ряду (рис. 10). ПРИМЕР. Составим вспомогательную таблицу (рис. 17).
Рис. 17. Таблица для расчета коэффициентов уравнения тренда. В этом случае система уравнений для отыскания a и b записывается в следующем виде: 28 a + 7 b = 56; 140 a + 28 b = 223. Решая систему, получаем: a = (– 1/28) ≈ - 0,04; b = 57/7 ≈ 8,14. Тем самым уравнение искомого тренда имеет вид: x = – 0,04 t + 8,14. Расчет показателя на следующий день проводится так: Графическое изображение тренда представлено на рисунке 18. 11 - 10 - - 8 - - 6 - - 4 - - 2 - -
1 2 3 4 5 6 7 8 Рис. 18. Метод проецирования тренда. ЗАМЕЧАНИЕ. Точность прогноза можно оценить при помощи коэффициента корреляции. Приведенные методы далеко не исчерпывают многообразия методов анализа временных рядов, большинство которых опирается не на простой подсчет при помощи калькулятора, но на основательную аналитическую и компьютерную базу. Однако наша цель состоит в том, чтобы дать определенное рабочее представление об этом типе прогнозирования. 3. ТРЕНДОВЫЕ МОДЕЛИ, СОДЕРЖАЩИЕ СЕЗОННУЮ КОМПОНЕНТУ. В большинстве случаев значения переменных характеризуют не только тренд. Часто они подвержены циклическим колебаниям. Если эти колебания повторяются в течение небольшого промежутка времени, то они называются сезонной вариацией. Колебания, повторяющиеся в течение более длительного промежутка времени, называются циклической вариацией. Модель, содержащая сезонную компоненту, которая будет рассмотрена на этой лекции, основана на традиционном понятии сезона, однако, в более широком смысле термин «сезон» в прогнозировании применим к любым систематическим колебаниям. Например, при изучении товарооборота в течение недели под термином «сезон» подразумевается 1 день. При исследовании транспортных потоков дня или в течение недели также может использоваться модель с сезонной компонентой. Любые колебания относительно тренда, построенного по годовым значениям некоторого показателя, можно описать в виде модели с циклической компонентой. Не будем рассматривать примеры с циклическим фактором. Этот фактор можно выявить только по данным за длительные промежутки времени в 10, 15 или 20 лет, однако в данном случае колебания значений тренда могут быть вызваны воздействием общеэкономических факторов. Остановимся подробнее на моделировании более коротких промежутков времени, и не будем учитывать воздействие циклической компоненты. Последняя предпосылка нашей модели также следует из метода линейной регрессии. Она связана со значением ошибки, или остатка, т.е. той части значения наблюдения, которую нельзя объяснить с помощью построенной модели. ВЕЛИЧИНУ ОШИБОК МОЖНО ИСПОЛЬЗОВАТЬ В КАЧЕСТВЕ МЕРЫ СТЕПЕНИ СООТВЕТСТВИЯ МОДЕЛИ ИСХОДНЫМ ДАННЫМ. Обычно применяют два вида таких мер. 1) Cреднее абсолютное отклонение (mean absolute deviation — MAD) вычисляется по формуле: где xi - фактические значения показателя, fi - прогнозные значения показателя. Таким образом, MAD равно отношению суммы величин всех ошибок без учета их знака к общему числу наблюдений. 2) Среднеквадратическая ошибка (mean square error — MSE): Таким образом, MSE представляет собой отношение суммы квадратов ошибок к общему числу наблюдений. Последняя из указанных мер резко возрастает при наличии высоких ошибок. В процессе анализа временного ряда мы стараемся определить все имеющиеся факторы и построить модель, которая соответствующим образом отражала бы их. ПРИМЕР 2. Предположим, что объем продаж продукции компании в течение последних 13 кварталов представлен в таблице (рис. 19).
Рис. 19. Количество продукции, проданной в течение последних 13 кварталов. Необходимо проанализировать указанное множество данных и установить, можно ли обнаружить тенденцию. Если устойчивая тенденция действительно существует, данная модель будет использоваться нами для прогнозирования количества проданной продукции в следующие кварталы. Составим диаграмму временного ряда (рис. 20). Объем продаж
500 - 400 -
300 -
200 -
100 -
1 2 3 4 1 2 3 4 1 2 3 4 1 Время Рис. 20. Диаграмма временного ряда. Моделью с аддитивной компонентой называется такая модель, в которой вариация значений переменной во времени наилучшим образом описывается через сложение отдельных компонент. Предположив, что циклическая вариация не учитывается, модель фактических значений переменной X можно представить следующим образом: X = FT + S + Е, где X – фактическое значение, FТ – трендовое значение, S – сезонная вариация, E – ошибка. ЗАМЕЧАНИЕ. Приблизительно равная сезонная вариация (рис. 20) указывает на существование аддитивной модели. РЕШЕНИЕ. Будем использовать диаграмму моментного временного ряда. При построении диаграммы временного ряда полезно последовательно соединить точки отрезками, чтобы более четко увидеть любую тенденцию. Как следует из диаграммы (рис. 20), возможен возрастающий тренд, содержащий сезонные колебания. Объемы продаж в зимний период (1 и 4 кварталы) значительно выше, чем в летний (2 и 3 кварталы). Сезонная компонента практически не изменится в течение трех лет. Тренд показывает, что в целом объем продаж возрос примерно с 230 тыс. шт. в 2012 году до 390 тыс. шт. в 2014 году, однако увеличения сезонных колебаний не произошло. Этот факт свидетельствует в пользу модели с аддитивной компонентой. Проведем анализ модели с аддитивной компонентой:X = FT+S + E. В моделях, как с аддитивной, так и с мультипликативной компонентой, общая процедура анализа примерно одинакова: Шаг 1. Расчет значений сезонной компоненты. Шаг 2. Вычитание сезонной компоненты из фактических значений. Этот процесс называется десезонализацией данных. Расчет тренда на основе полученных десезонализированных данных. Шаг 3. Расчет ошибок как разности между фактическими и трендовыми значениями. Шаг 4. Расчет среднего отклонения (MAD) или среднеквадратической ошибки (MSE) для обоснования соответствия модели исходным данными или для выбора из множества моделей наилучшей. 1) Расчет сезонной компоненты в аддитивных моделях. ПРИМЕР 2 (продолжение). Вернемся к примеру 2, в котором рассматриваются квартальные объемы продаж компании за последние 13 кварталов. Мы уже выяснили, что этим данным отвечает аддитивная модель, т.е. фактически объемы продаж можно выразить следующим образом: X = FT + S + Е. Для того чтобы элиминировать влияние сезонной компоненты, воспользуемся методом скользящего среднего. Просуммировав первые четыре значения, получим общий объем продаж в 2012 году. Если поделить эту сумму на четыре, можно найти средний объем продаж в каждом квартале 2012 года, т. е. (239 + 201 + 182 + 297)/4 = 919/4 = 229,75. Полученное значение уже не содержит сезонной компоненты, поскольку представляет собой среднюю величину за год. У нас появилась оценка значения тренда для середины года, т.е. для точки, лежащей в середине между кварталами II и III. Если последовательно передвигаться вперед с интервалом в три месяца, можно рассчитать средние квартальные значения на следующих промежутках. апрель 2012 года — март 2013 года: (201 + 182 + 297 + 324)/4 = 1004/4 = 251, июль 2012 – июнь 2013: (182 + 297 + 324 + 278)/4 = 1081/4 = 270,25; … апрель 2014 года - март 2015 года: (360 + 335 + 462 + 481)/4 = 1638/4 = 409,5. Данная процедура позволяет генерировать скользящие средние по четырем точкам для исходного множества данных. Получаемое таким образом множество скользящих средних представляет наилучшую оценку искомого тренда. Теперь полученные значения тренда можно использовать для нахождения оценок сезонной компоненты. Мы рассчитываем: X – FT = S + E. К сожалению, оценки значений тренда, полученные в результате расчета скользящих средних по четырем точкам, относятся к несколько иным моментам времени, чем фактические данные. Первая оценка, равная 229,75, представляет собой точку, совпадающую с серединой 2012 года, т.е. лежит в центре промежутка фактических значений объемов продаж во II и III кварталах. Вторая оценка, равная 251, лежит между фактическими значениями в III и IV кварталах 2012 года. НАМ ЖЕ ТРЕБУЮТСЯ ДЕСЕЗОНАЛИЗИРОВАННЫЕ СРЕДНИЕ ЗНАЧЕНИЯ, СООТВЕТСТВУЮЩИЕ ТЕМ ЖЕ ИНТЕРВАЛАМ ВРЕМЕНИ, ЧТО И ФАКТИЧЕСКИЕ ЗНАЧЕНИЯ ЗА КВАРТАЛ. Положение десезонализированных средних во времени сдвигается путем дальнейшего расчета средних для каждой пары значений. Найдем среднюю из первой и второй оценок, центрируя их на июль-сентябрь 2012 года, т. е. (229,75 + 251) / 2 = 240,375 ≈ 240,4. Это и есть десезонализированная средняя за июль-сентябрь 2012 года. Эту десезонализированную величину, которая называется центрированной скользящей средней, можно непосредственно сравнивать с фактическим значением за июль-сентябрь 2012 года, равным 182. Отметим, что это означает отсутствие оценок тренда за первые два или последние два квартала временного ряда. Результаты этих расчетов приведены в следующей таблице (рис. 21).
Рис. 21. Расчет по 4 точкам центрированных скользящих средних значений тренда для модели X= FT + S + Е. Для каждого квартала мы имеем оценки сезонной компоненты, которые включают в себя ошибку или остаток. Прежде чем мы сможем использовать сезонную компоненту, нужно пройти два следующих этапа. Найдем средние значения сезонных оценок для каждого сезона года. Эта процедура позволит уменьшить некоторые значения ошибок. Наконец, скорректируем средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы общая их сумма была равна нулю. Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год. Корректирующий фактор рассчитывается следующим образом: сумма оценок сезонных компонент делится на 4. В последнем столбце таблицы (рис. 21) эти оценки записаны под соответствующими квартальными значениями. Сама процедура приведена в следующей таблице (рис. 22).
Рис. 22. Расчет средних значений сезонной компоненты. В данном случае производилось округление двух значений сезонной компоненты до ближайшего большего числа, а двух значении — до ближайшего меньшего числа таким образом, чтобы общая сумма была равна нулю. Значения сезонной компоненты еще раз подтверждают наши выводы, сделанные на основе диаграммы (рис. 20). Объемы продаж за два зимних квартала превышают среднее трендовое значение приблизительно на 40 тыс. шт., а объемы продаж за два летних периода ниже средних на 21 и 62 тыс. шт. соответственно. ЗАМЕЧАНИЕ. Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Если, например, в качестве сезонов выступают дни недели, для элиминирования влияния ежедневной «сезонной компоненты» также рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, т.е. в четверг; таким образом, необходимость в процедуре центрирования отпадает. 2) Десезонализация данных при расчете тренда. Шаг 2. Состоит в десезонализации исходных данных. Она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал (то есть X — S = FT + Е), что показано ниже (рис. 23).
Рис. 23. Расчет десезонализированных данных. Новые оценки значений тренда, которые еще содержат ошибку, можно использовать для построения модели основного тренда. Если нанести эти значения на исходную диаграмму (рис. 24), можно сделать вывод о существовании явного линейного тренда.  Объем продаж Объем продаж
400 -
300 -
200 -
100 - 1 2 3 4 1 2 3 4 1 2 3 4 1 Время Рис. 24. Графическое изображение линии тренда. Уравнение линии тренда имеет вид: FТ (m) = аm + b, где m — номер квартала; коэффициенты a и b характеризуют точку пересечения с осью ординат и угол наклона линии тренда к временной оси. Для определения параметров a, b прямой, наилучшим образом аппроксимирующей тренд, можно использовать метод наименьших квадратов. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ [1] Грешилов А. Α., Стакун В. Α., Стакун А. А. Математические методы построения прогнозов.— М.: Радио и связь, 1997.— 112 с; ил. [2] Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. — М.: ЮНИТИ- ДАНА, 2001. - 367 с. [3] Шикин Е. В., Чхартишвили А. Г. Математические методы и модели в управлении: Учеб. пособие. — 3-е изд. — М.: Дело, 2004. — 440 с. — (Сер. "Классический университетский учебник"). [4] Эддоус М., Стенсфилд Р. Методы принятия решений. М.: ЮНИТИ, 1997. [5] Экономико-математические методы и прикладные модели: Учебное пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. — М.: ЮНИТИ, 1999. - 391 с. ОГЛАВЛЕНИЕ ДИССЕРТАЦИИдоктор экономических наук Ермолаев, Михаил Борисович ф Введение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

