Ответы. Модуль непрерывности функции одной переменной на множестве. Равномерная непрерывность
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
13. Интегрирование по частям. Признаки Абеля и Дирихле. Рассмотрим 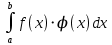 , где , где 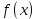 - непрерывна на - непрерывна на 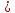 , , 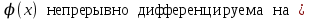 . .Пусть 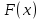 – первообразная – первообразная 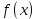 , тогда , тогда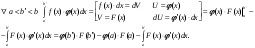 Если существует 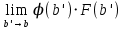 - конечный и существует - конечный и существует 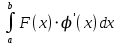 - сходящийся, то существует - сходящийся, то существует 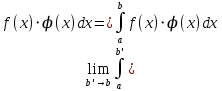 , то есть интеграл сходящийся. , то есть интеграл сходящийся.Первый признак сходимости (Абеля). Если 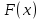 ограничена на ограничена на 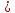 , , 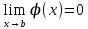 и и 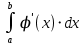 - сходящийся абсолютно, то - сходящийся абсолютно, то 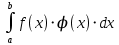 - сходящийся. - сходящийся.Доказательство: Рассмотрим 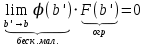 Рассмотрим 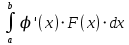 , он абсолютно сходящийся: , он абсолютно сходящийся: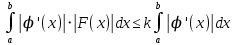 - сходящийся по условию. Значит, - сходящийся по условию. Значит, интеграл сходится. Признак Дирихле. Если 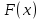 - ограниченная на - ограниченная на 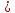 , знакопостоянная , знакопостоянная 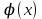 монотонно стремится к 0 при монотонно стремится к 0 при 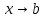 , то интеграл сходящийся. , то интеграл сходящийся.Доказательство: Так как 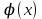 - знакопостоянная, то меняя знак, мы всегда можем добиться того, чтобы - знакопостоянная, то меняя знак, мы всегда можем добиться того, чтобы 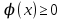 . Рассмотрим этот случай. . Рассмотрим этот случай.Очевидно, 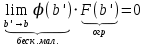 Надо доказать, что 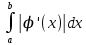 – сходится. Рассмотрим случай – сходится. Рассмотрим случай 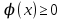 , с учетом невозрастания , с учетом невозрастания 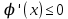 , тогда , тогда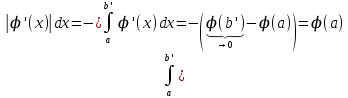 - сходится, тогда исходный интеграл сходящийся по первому признаку. - сходится, тогда исходный интеграл сходящийся по первому признаку.Пример. Исследуем на сходимость 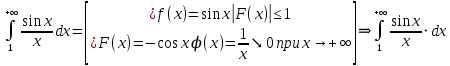 – – сходящийся. 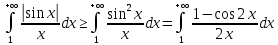 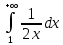 - расходящийся, а - расходящийся, а 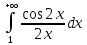 - сходящийся по признаку Дирихле, значит и весь исходный интеграл расходится. Таким образом, - сходящийся по признаку Дирихле, значит и весь исходный интеграл расходится. Таким образом, 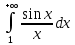 сходится условно. сходится условно.14. Гамма-функция Эйлера. Определение, сходимость, свойства. О. Пусть задано число 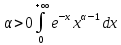 – сходится и его значение = Г( – сходится и его значение = Г(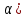 Рассмотрим интеграл 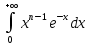 . . 1) n=1 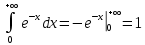 Далее рассмотрим интеграл 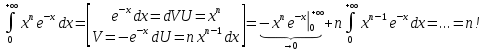 Положим 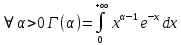 . Исходя из предыдущего, если . Исходя из предыдущего, если 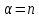 - натуральное, то - натуральное, то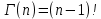 Докажем корректность( то есть, что интеграл сходится): Если 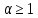 , то единственная особенность в точке , то единственная особенность в точке 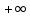 . .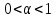 - две особенности: 0; - две особенности: 0; 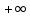 . .Чтобы сразу захватывать оба случая, рассмотрим интеграл отдельно на двух промежутках. 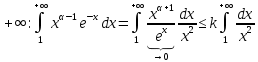 - сходится вне зависимости от - сходится вне зависимости от 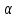 . .Рассмотрим этот интеграл при 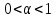 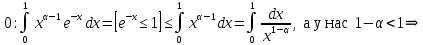 интеграл сходится. Таким образом, исходный интеграл сходится при любом положительном интеграл сходится. Таким образом, исходный интеграл сходится при любом положительном 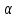 . .При доказательстве того, что 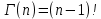 у нас получилось свойство: у нас получилось свойство: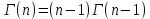 . В доказательстве не было существенно, какое n. . В доказательстве не было существенно, какое n.Если в доказательстве этого равенства вместо 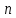 поставить произвольное положительное поставить произвольное положительное 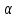 , ничего не изменится, следовательно, мы получим свойство гамма-функции: , ничего не изменится, следовательно, мы получим свойство гамма-функции: 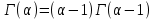 Таким образом, гамма-функция Эйлера – обобщение понятие факториала на все положительные числа. 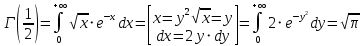 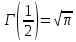 15. Открытые и замкнутые множества. Рассмотрим про-во 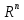 ,состоящее из точек ,состоящее из точек 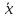 с координатами с координатами  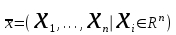 Расстояние между двумя точками: 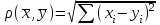 - Евклидова метрика. - Евклидова метрика.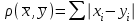 ; ; 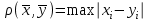 Замкнутым шаром с центром в 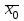 и радиусом и радиусом 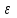 называется множество точек называется множество точек 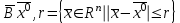 Открытый шар : 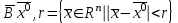 Определение: точка 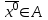 называется внутренней точкой множества A, если она принадлежит A вместе с некоторым открытым шаром называется внутренней точкой множества A, если она принадлежит A вместе с некоторым открытым шаром 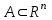 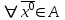 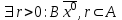 множество, у которого все точки внутренние называется открытым. Примеры: 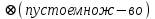 является открытым является открытым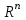 - открытое - открытое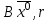 - открытое - открытое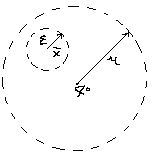 Док-во: Возьмем произвольную т. 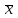 из открытого шара, тогда: из открытого шара, тогда: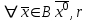 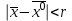 возьмем возьмем 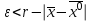 , тогда рассмотрим шар с центром в точке , тогда рассмотрим шар с центром в точке 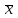 и радиусом и радиусом 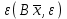 : тогда : тогда 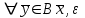 по нер-ву треуг. по нер-ву треуг. 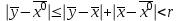 т.е. любая точка, принадлежащая маленькому шару, принадлежит и большому шару. (т.к. т.е. любая точка, принадлежащая маленькому шару, принадлежит и большому шару. (т.к.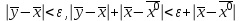 , а мы брали , а мы брали 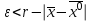 , поэтому , поэтому 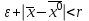 , а значит и , а значит и 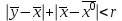 ) )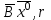 - не открытое - не открытое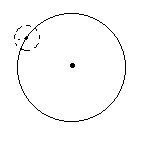 если взять 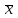 такую что такую что 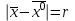 , то , то 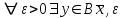 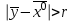 Определение: предельная точка множества А: Если в 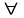 шаре (в её окрестности) содержатся эл-ты множества А шаре (в её окрестности) содержатся эл-ты множества АЕсли точка принадлежит множеству А. Точка называется граничной, если в любой её окрестности есть и точки принадлежащие множеству и точки, не принадлежащие множеству. Множество, содержащее все свои предельные, точки называется замкнутым. Пустое множество является одновременно откр и замк. А - открытое 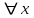 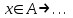 A – пустое 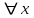 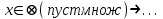 множество открытое множество открытоеА – замкнутое 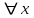 х- предельное х- предельное 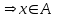 (пустое множество) – предельных точек нет А- замкнуто , то 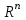 – А открыто – А открытоА – открыто, то 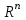 – А замкнуто – А замкнутоТеорема : Дополнение множ-ва А- открытое 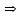 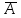 - замкнуто - замкнутоПредположим, что 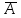 не замкнуто. не замкнуто. 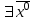 предельная точка предельная точка 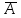 , , 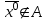 . .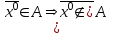 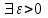 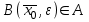 Но 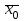 - предельная точка - предельная точка 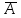 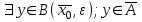 Противоречие : 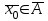 , , 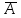 - замкнуто - замкнутоА – замкнуто 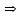 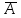 - открыто - открытоНужно доказать : 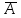 - открыто т.е. - открыто т.е. 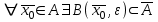 Предположим 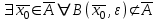 Значит 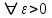 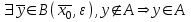 Значит 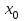 - предельная точка для А, аА замкнуто, - предельная точка для А, аА замкнуто, 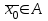 - противоречие. - противоречие.16. Предел последовательности в 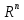 . Теорема Больцано-Вейерштрасса. . Теорема Больцано-Вейерштрасса.Предел последовательности – это последовательность точек 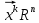 ; ;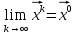 , если >0 , если >0 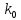 k> k>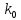 ; ( ; (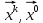 )< )<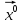 – предельная точка множества А, когда { – предельная точка множества А, когда {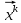 }, }, 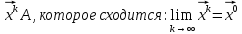 ; ; Ограниченное мн-во: А – огр., если С АВ( 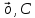 ); ( ); (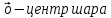 ) ) 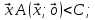 Утверждение: Пусть { 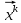 } сходится только тогда, когда имеет место покоординатная сходимость. } сходится только тогда, когда имеет место покоординатная сходимость.i, 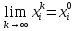 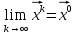 Д-во: >0 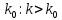 ( (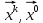 ) <; ( ) <; (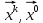 ) = ) = 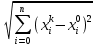 | |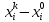 |; |;i | 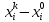 |<; |<; 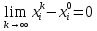 ; ; i 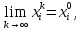 тогда для каждой координаты тогда для каждой координаты 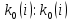 будет справедливо будет справедливо | 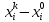 |< |<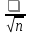 ; ; 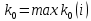 ; k> ; k>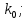 тогда ( тогда (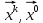 ) = ) = 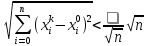 =; =;Теорема Больцано-Вейерштрасса Из любой ограниченной п-ти можно выделить сходящуюся подпоследовательность. Д-во: Пусть последовательность 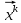 ограничена: | ограничена: |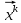 | |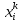 }< | }< |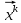 | |Сначала извлекаем сходящуюся последовательность из последовательности 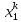 : она ограничена, поэтому из нее можно извлечь сходящуюся подпоследовательность: : она ограничена, поэтому из нее можно извлечь сходящуюся подпоследовательность: 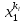 сход. сход. 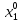 .Теперь рассмотрим подпоследовательность второй координаты .Теперь рассмотрим подпоследовательность второй координаты 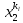 : она тоже является ограниченной, значит из нее можно извлечь сходящуюся подпоследовательность : она тоже является ограниченной, значит из нее можно извлечь сходящуюся подпоследовательность 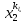 , при этом последовательность , при этом последовательность 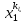 , осталась сходящейся. , осталась сходящейся. 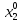 , потому что , потому что 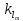 - подпоследовательность - подпоследовательность 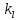 , и т.д. Т.е. когда мы получили подпоследовательность , и т.д. Т.е. когда мы получили подпоследовательность 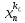 , то она будет сходящейся, и все остальные последовательности координат тоже при этом остаются сходящимися. Значит, и , то она будет сходящейся, и все остальные последовательности координат тоже при этом остаются сходящимися. Значит, и 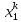 - тоже сходится, т.к. есть покоординатная сходимость. Теорема доказана. - тоже сходится, т.к. есть покоординатная сходимость. Теорема доказана. |
