Ответы. Модуль непрерывности функции одной переменной на множестве. Равномерная непрерывность
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
21. Производная сложной функции и производная по направлению. Градиент. Рассмотрим для удобства записи функцию трех переменных, т.к. случай трех переменных легко распространяются на n. Пустьf(x,y,z) дифференцируема в точке 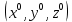 . Пусть . Пусть 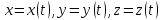 , где , где 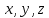 дифференцируемы в точке дифференцируемы в точке 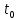 , причем , причем 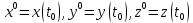 , тогда можно рассмотреть функцию , тогда можно рассмотреть функцию 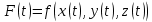 - функция одной переменной. Эта функция будет дифференцируема в точке - функция одной переменной. Эта функция будет дифференцируема в точке 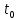 . .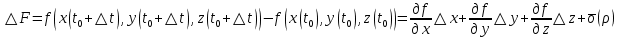 - т.к. функция дифференцируема по условию. - т.к. функция дифференцируема по условию.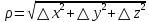 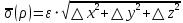 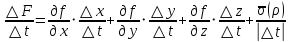 Когда мы  устремляем к нулю, устремляем к нулю, 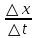 стремится к стремится к 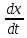 , , 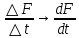 и т.д, остается только доказать, что и т.д, остается только доказать, что 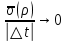 . .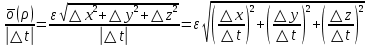 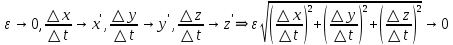 Таким образом, устремив 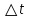 к нулю, получаем: к нулю, получаем: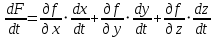 22. Касательная плоскость. Уравнение касательной плоскости для поверхностей, заданных явным и неявным образом. Рассмотрим функцию 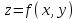 дифф в дифф в 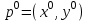 Построим плоскость: П: 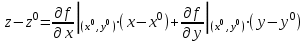 , где , где 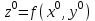 Рассмотрим поверхность Г: 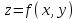 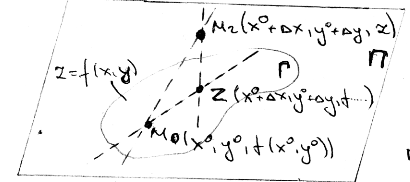 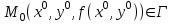 Плоскость П тоже проходит через 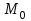 . Возьмем произвольное приращение . Возьмем произвольное приращение 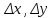 и рассмотрим точку и рассмотрим точку 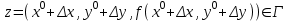 Рассмотрим соответствующую точку на П - 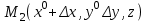 Измерим расстояние между точками 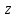 и и 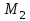 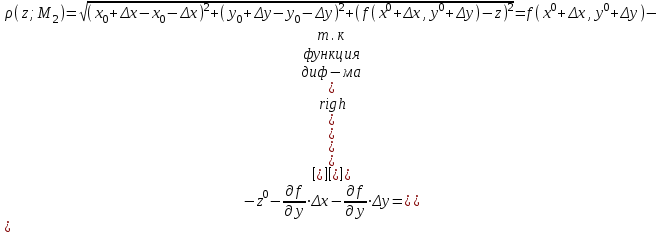 где 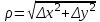 Плоскость, такая, что расстояние от этой пл-ти до поверхности вдоль оси zстремится к нулю быстрее, чем расстояние между точками на пл-ти называется касательной. В обратную сторону рассуждения тоже верны: Если пл-ть: 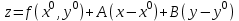 является касательной, то ф-я является касательной, то ф-я 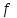 - дифференцируема, при этом - дифференцируема, при этом 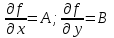 23. Производная по направлению. Градиент. - единичный вектор || = 1 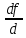 = =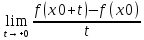 =F’(t) =F’(t)(cos 1, cos 2,……,cos n) = tx f(x) xi=xi0+t F’(t) = 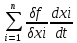 = = 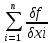 i = (grad f, ) i = (grad f, )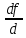 = F’(t) = |grad f||| = (grad f) => grad f” = F’(t) = |grad f||| = (grad f) => grad f”|grad f| = ( 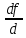 )max )max24. Дифференциал высших порядков. Инвариантность первого дифференциала. 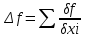 | x0 | x0Зафиксируем приращение, тогда: 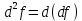 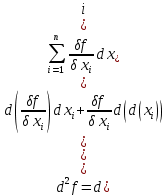 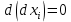 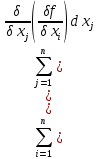 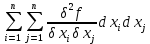 f(x) где х – независимая переменная 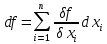 x = x(t) f(x) = f(x(t)) 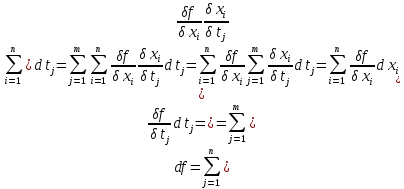 Форма первого дифференциала инвариантна 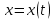 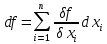 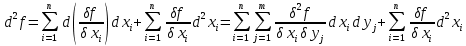 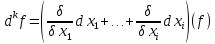 25. Формула Тейлора для функции многих переменных. 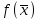 - непрерывная функция - непрерывная функцияПусть 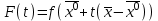 тогда: тогда: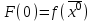 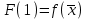 Раскладываем F(t) по формуле Тейлора в точке t=1 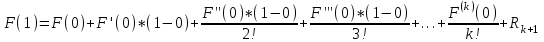 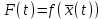 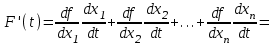 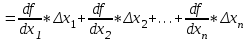 - дифференциал в - дифференциал в 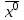 т.е. т.е. 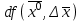 Делаем обратную замену: 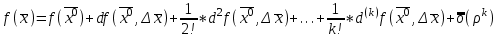 26. Локальный экстремум функции многих переменных. Необходимое условие. Достаточное условие. Локальный экстремум функции многих переменных. Пусть функция F определена на некоторой области 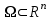 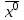 называется точкой локального максимума, если называется точкой локального максимума, если 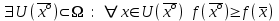 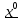 называется точкой локального минимума, если называется точкой локального минимума, если 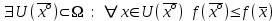 Пусть 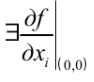 тогда тогда 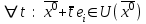 где где 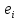 - координатный вектор i-го направления, - координатный вектор i-го направления,в случае максимума получаем: 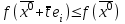 Теперь рассмотрим 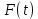 - функцию одной переменной: - функцию одной переменной: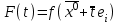 максимум этой функции достигается при t=0 . максимум этой функции достигается при t=0 .Необходимым условием существования точки максимума для функции одной переменной является равенство нулю первой производной, значит 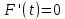 a a 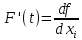 - производная по направлению - производная по направлению 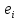 Таким образом, необходимое условие существования экстремума – равенство нулю всех частных производных, по всем направлениям, при условии их существования. Достаточное условие. Пусть в 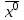 выполняется необходимое условие и существуют непрерывные вторые производные выполняется необходимое условие и существуют непрерывные вторые производные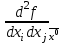 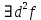 если для любого не нулевого набора приращений 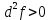 т.е. т.е.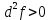 при при 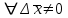 то то 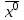 -точка минимума. -точка минимума.если для любого не нулевого набора приращений 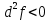 т.е. т.е.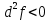 при при 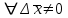 то то 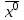 -точка максимума. -точка максимума.если 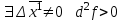 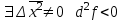 то экстремума нет. если для всех приращений 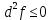 или или 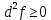 т.е. т.е.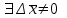 такое что такое что 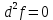 то ничего сказать нельзя, требуется дополнительное исследование. то ничего сказать нельзя, требуется дополнительное исследование.27. Неявные функции и системы неявных функций Понятие неявной функции. Рассмотрим уравнением F(x,y)=0. Пусть для любого х из множества Х это уравнение имеет решение относительно у. Тем самым каждому х ставится в соответствие определенное число у. Если уравнение имеет несколько решений относительно у, то выбираем одно из них. Таким образом, на множестве Х определена функция y=f(x). При этом правило f, по которому ставится соответствие не указано явно, а задано с помощью уравнения F(x,y)=0. Такая функция называется неявной. Аналогично можно определить неявную функцию нескольких переменных y=f(x1,x2,…,xn) как решения уравнения F(x1,x2,…,xn)=0 относительно у. Существование и непрерывность неявной функции. Теорема. Пусть функция F(x,y) непрерывна в прямоугольнике 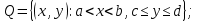 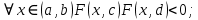 (на нижней и верхней сторонах прямоугольника Q функция 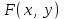 имеет значения разных знаков); имеет значения разных знаков); 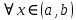 функция F(x,y) является строго монотонной функцией аргумента у на отрезке [c,d]. функция F(x,y) является строго монотонной функцией аргумента у на отрезке [c,d].Тогда на 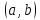 существует единственная неявная функция y=f(x), определяемая уравнением F(x,y)=0, и эта функция непрерывна на существует единственная неявная функция y=f(x), определяемая уравнением F(x,y)=0, и эта функция непрерывна на 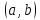 . .Неявные функции, определяемые системой уравнений. Рассмотрим систему уравнений 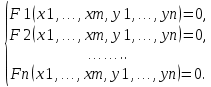 Решение этой системы 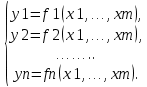 называется совокупностью неявных функций, определяемых системой уравнений. Определитель  , ,составленный из частных производных, называется определителем Якоби, или якобианом функций 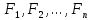 по переменным по переменным 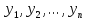 и обозначается и обозначается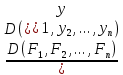 . .Теорема. Пусть функции 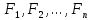 дифференцируемы в некоторой окрестности точки дифференцируемы в некоторой окрестности точки 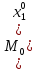 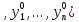 ; ;частные производные 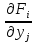 (i,j=1,2,…m) непрерывны в точке (i,j=1,2,…m) непрерывны в точке 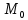 ; ;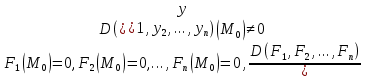 . .Тогда существует такой параллелепипед 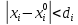 (i=1,2,…m), (i=1,2,…m),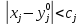 (j=1,2,…n), (j=1,2,…n),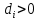 , , 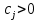 , в окрестности точки , в окрестности точки 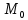 , в котором система определяет единственную совокупность неявных функций и эти функции дифференцируемы при , в котором система определяет единственную совокупность неявных функций и эти функции дифференцируемы при 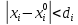 (i=1,2,…m), (i=1,2,…m),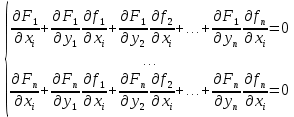 Якобиан системы отличен от нуля, поэтому система определенная, и из нее однозначно определяются частные производные неявных функций. 28. Условный экстремум. Необходимое условие. Дифференциальные уравнения связи. Достаточное условие условного экстремума. Рассмотрим задачу нахождения локального экстремума функции f(x,y), если накладываются дополнительные условия, ограничивающие область изменения аргумента. Определение. Функция f(x,y) имеет условный максимум (условный минимум) в точке P0(x0,y0), если существует такая окрестность точки P0, что 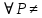 P0, удовлетворяющей уравнению связи P0, удовлетворяющей уравнению связи 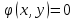 , выполняется неравенство f(P0)>f(P) (f(P0) , выполняется неравенство f(P0)>f(P) (f(P0)В отличие от задачи определения точек экстремума функции многих переменных в данной задаче появляется дополнительное условие: точки экстремума удовлетворяют равенству 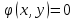 . Для решения задач нахождения условных экстремумов используется метод неопределенных множителей Лагранжа. Функция Лагранжа определяется следующим образом: . Для решения задач нахождения условных экстремумов используется метод неопределенных множителей Лагранжа. Функция Лагранжа определяется следующим образом: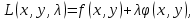 , где 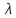 – множитель Лагранжа. – множитель Лагранжа.Теорема. (Необходимые условия условного экстремума) Пусть функции f(x,y), 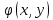 – непрерывны и имеют частные производные первого порядка. Тогда в точке условного экстремума – непрерывны и имеют частные производные первого порядка. Тогда в точке условного экстремума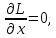 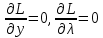 . .Покажем, что в точке условного экстремума линия уровня функции f(x,y) касается кривой 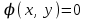 . .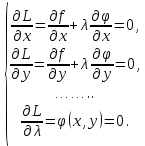 Напомним, что векторы градиентов имеют координаты gradf= 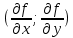 , grad , grad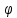 = =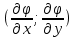 . Из последней системы следует, что gradf+grad . Из последней системы следует, что gradf+grad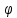 =0, значит, векторы градиентов параллельны. Вектор градиента функции f(x,y) в заданной точке перпендикулярен касательной к линии уровня в этой точке. Таким образом, в точке условного экстремума есть касание некоторой линии уровня f(x,y)=c и кривой =0, значит, векторы градиентов параллельны. Вектор градиента функции f(x,y) в заданной точке перпендикулярен касательной к линии уровня в этой точке. Таким образом, в точке условного экстремума есть касание некоторой линии уровня f(x,y)=c и кривой 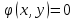 . .Теорема. (Достаточные условия условного экстремума) Пусть P0(x0,y0), 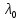 – решение системы из теоремы о необходимых условиях условного экстремума, – решение системы из теоремы о необходимых условиях условного экстремума,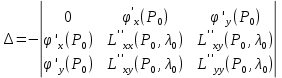 . .Если 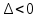 , то f(x,y) имеет условный максимум в точке P0(x0,y0), , то f(x,y) имеет условный максимум в точке P0(x0,y0),если 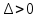 , то f(x,y) имеет условный минимум в точке P0(x0,y0). , то f(x,y) имеет условный минимум в точке P0(x0,y0).29. Замена переменных в дифференциальных выражениях. 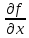 , , 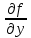 - зависит от них→ - зависит от них→ 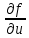 , , 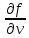 надо к этому перейти. надо к этому перейти.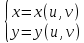 ← диффер. по x ← диффер. по x f(u(x,y),v(x,y)) 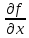 = = 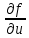 * *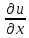 + + 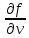 * *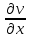 (1) надо избавиться от (1) надо избавиться от 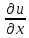 и и 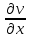 . .  → отсюда выражаем → отсюда выражаем  и и  и подставляем в (1). и подставляем в (1). |
