Ответы. Модуль непрерывности функции одной переменной на множестве. Равномерная непрерывность
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Модуль непрерывности функции одной переменной на множестве. Равномерная непрерывность. Равномерная непрерывность функций, непрерывных на отрезке. Определенный интеграл Римана. Эквивалентные определения. Примеры интегрируемых и неинтегрируемых функций. Необходимое условие существования интеграла Римана. Суммы Дарбу. Свойства. Суммы Дарбу и интегрируемость функции по Риману. Свойства определённого интеграла: аддитивность, однородность, неравенства, теоремы о среднем. Интеграл как функция верхнего предела. Непрерывность. Дифференцируемость интеграл как функция верхнего предела. Теорема Ньютона-Лейбница. Несобственные интегралы. Определение. Виды. Сходимость. Критерий Коши. Несобственные интегралы от неотрицательных функций. Признак сравнения, предельный признак сравнения, частный признак сравнения с интегралами 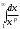 , , 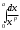 . .Абсолютно сходящиеся интегралы. Интегрирование по частям. Признаки Абеля и Дирихле. Гамма-функция Эйлера. Определение. Сходимость. Свойства. Внутренние, предельные, граничные точки множества в 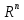 . Открытые и замкнутые множества в . Открытые и замкнутые множества в 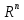 . . Предел последовательности в 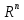 . Теорема Больцано-Вейерштрасса . Теорема Больцано-ВейерштрассаПредел функции нескольких переменных. Свойства. Предел по направлению. Непрерывность функции нескольких переменных. Непрерывность функции на замкнутом множестве. Частные производные. Дифференцируемость функции нескольких переменных, дифференциал. Необходимые условия дифференцируемости. Достаточное условие дифференцируемости. Производная сложной функции. Касательная плоскость. Уравнение касательной плоскости для поверхностей, заданных явным и неявным образом. Производная по направлению. Градиент. Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Формула Тейлора для функции многих переменных. Локальный экстремум функции многих переменных. Необходимое условие. Достаточное условие. Неявные функции и системы неявных функций. Условный экстремум. Необходимое условие. Дифференциальные уравнения связи. Достаточное условие условного экстремума. Замена переменных в дифференциальных выражениях. Модуль непрерывности функции одной переменной на множестве. Môđun tính liên tục của một hàm một biến trên một tập hợp Равномерная непрерывность. Tính liên tục đồng nhất. Для любой ограниченной на множестве А ф-ции можно ввести понятие модуля непрерывности Модуль непрерывности ф-ции f на множестве А – определённая как: 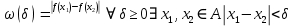 Свойства модуля: Если 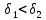 , тогда , тогда 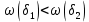 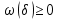 для любого для любого 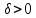 Равномерная непрерывность Пусть f ограничена на множестве А ( 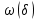 – модуль непрерывности f) – модуль непрерывности f)Если 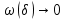 при при 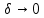 , иными словами, если , иными словами, если 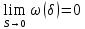 , то ф-ция называется равномерно непрерывной на множестве А , то ф-ция называется равномерно непрерывной на множестве АФ-ция f называется равномерно непрерывной на множестве А, если 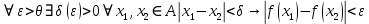 Определения 1 и 2 эквивалентны Равномерная непрерывность функций, непрерывных на отрезке. Tính liên tục đồng nhất của các hàm liên tục trong một khoảng thời gian Т. Если ф-ция f определена на отрезке [a,b] и непрерывна на нём, она является равномерно непрерывной на данном отрезке Докажем теорему “от противного” Пусть f непрерывна на отрезке [a,b], но не является равномерно непрерывной на нём, тогда: 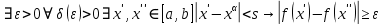 Зададим последовательность 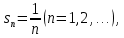 тогда тогда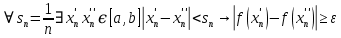 Последовательность {xn} ограничена, т.к. все её точки принадлежат отрезку [a,b], следовательно по теореме Больцано-Вейерштрассе из неё можно выделить сходящиеся последовательности: 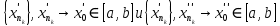 Получим 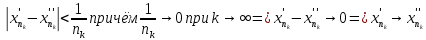 => они сходятся в одной и той же точке По условию f непрерывна на отрезке [a,b] => непрерывна в x0 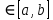 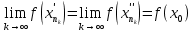 Перейдём теперь к пределу в неравенстве 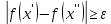 При 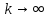 получим получим 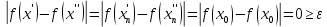 Получим, что 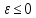 , но по условию наоборот. Противоречие. Теорема доказана , но по условию наоборот. Противоречие. Теорема доказана3. Определенный интеграл Римана. Эквивалентные определения. Примеры интегрируемых и неинтегрируемых функций. Пусть задана функция f(x) на отрезке 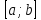 . Составим разбиение R: . Составим разбиение R: 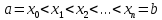 . .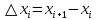 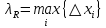 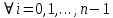 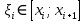 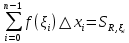 Это интегральная сумма, соответствующая разбиению R и выбору точек 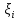 . .Если существует предел при 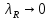 интегральных сумм интегральных сумм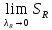 , и он не зависит от R и , и он не зависит от R и 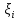 , то он называется определенным интегралом Римана. , то он называется определенным интегралом Римана.Определение по Коши: 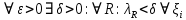 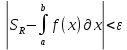 По Гейне: 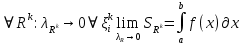 , где , где 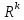 - последовательность разбиений. - последовательность разбиений.Критерий Коши: 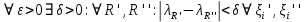 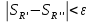 Если для ф-и f(x) на [a,b] существует определенный интеграл, то ф-ю f(x) назыв. интегрируемой по Риману на отрезке [a,b] и обозначают f(x) ϵ R[a,b]. Интегрировать по Риману можно след. ф-и: f(x) - непрер. на [a,b] f(x) – огранич. на [a,b], имеющая конечное число точек разрыва. Функция Дирихле не интегрируема 4. Необходимое условие существования интеграла Римана Если функция интегрируема на [a;b], то она ограничена на [a;b] Доказательство: 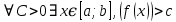 – неограниченная функция. – неограниченная функция.Пусть это не так (т.е. пусть ф-я неогр.). Тогда, на разбиении р существует минимум один такой участок [xj0;xj0+1 ], что на нем выполняется условие неограниченности. Тогда интегральная сумма будет выглядеть как: SR=f(ej0)* xj0 + ∑f(ej)* xj(в сумму входят все участки разбиения, кроме [xj0;xj0+1])=f(ej0)* xj0+A |SR|>=|f(ej0)|* xj0 - |A| Возьмем сколь угодно большое число N: |f(ej0)|* xj0 – |A|>N |f(ej0)|>(|A| + N)/ xj0 Т.к. на [xj0;xj0+1] f(x) неогр., то такая точка ej0 cуществует. Тогда, каким большим бы число N не было, при надлежащем выборе точек e интегральная сумма SR может быть получена большей, чем N, значит, предел интегральных сумм зависит от выбора точек функция не является интегрируемой на [a;b] 5. Суммы Дарбу. Их Свойства. Определение: Пусть 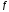 ограничена на отрезке ограничена на отрезке 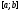 . Введём разбиение R этого отрезка. . Введём разбиение R этого отрезка.R: 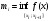 , , 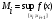 . .Тогда можем составить выражения: 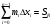 - нижняя сумма Дарбу, - нижняя сумма Дарбу, 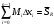 - верхняя сумма Дарбу. - верхняя сумма Дарбу.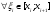 , , 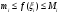 . .Свойства сумм Дарбу: 1) 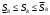 , для одного и того же разбиения. , для одного и того же разбиения.2) Рассмотрим два разбиения в случае, когда одно разбиение является продолжением другого. Т.е. 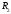 - продолжение - продолжение 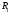 , если все точки , если все точки 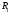 являются точками являются точками 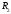 . .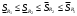 , ,т.е. добавление точек не увеличивает 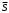 и не уменьшает и не уменьшает 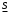 . . Доказательство:  Пусть Пусть  получается из получается из 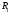 добавлением одной точки. добавлением одной точки.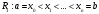 , , 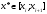 , , 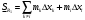 , ,  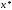 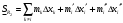 , ,Заметим, что если 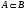 , то , то 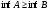 и и 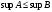 . Отсюда заключаем: . Отсюда заключаем: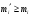 , , 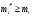 , , 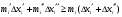 , , 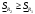 . Аналогично для . Аналогично для 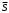 3) Для любых двух разбиений одного и того же отрезка нижняя сумма Дарбу не превосходит верхней: 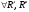 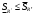 . .Доказательство: Пусть 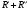 - объединение двух разбиений, тогда - объединение двух разбиений, тогда 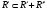 , , 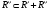 , тогда по свойству 2 , тогда по свойству 2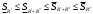 , т.е. , т.е. 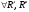 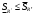 . .4) 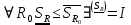  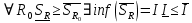 Пример: функция Дирихле 6. Суммы Дарбу и интегрируемость функции по Риману. Теорема: Функция 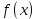 интегрируема на отрезке интегрируема на отрезке 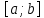 тогда и только тогда, когда тогда и только тогда, когда 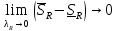 . .Доказательство: Докажем необходимость условия: Функция 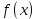 интегрируема на отрезке интегрируема на отрезке 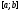 . .Пусть 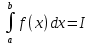 , тогда , тогда 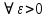 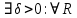 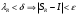 , т.е. , т.е.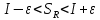 . .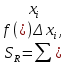 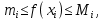 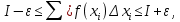 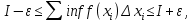 т.е.  и и  . . Далее имеем:  , т.е. , т.е.  . . Необходимость доказана. Докажем достаточность условия:  . .   . .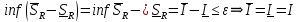 . .Докажем, что 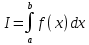 . .Нужно: 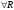 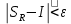 , т.е. , т.е. 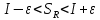 Имеем: 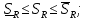 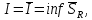 тогда по определению тогда по определению 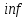   , , , тогда по определению , тогда по определению    , , т.е.   . .Достаточность доказана. |
