Ответы. Модуль непрерывности функции одной переменной на множестве. Равномерная непрерывность
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
7. Свойства определенного интеграла: аддитивность, однородность, неравенства, теоремы о среднем. Аддитивность: Функция f интегрируема на [a;b] ⇔ когда она интегрируем на [a;c] ∪ [c;b], c ∊ (a;b) и справедливо: 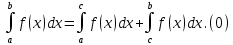 Д-во: ⊳Если 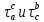 - разбиения соответственно отрезков [a;c] и [c;b], то объединение этих разбиений - разбиения соответственно отрезков [a;c] и [c;b], то объединение этих разбиений 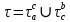 является разбиением [a;b], причём является разбиением [a;b], причём 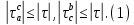 Пусть 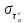 и и 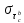 – интегральные суммы ф-ии f ⟹ – интегральные суммы ф-ии f ⟹ 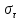 = =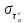 + + 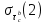 . И т.к. f интегрируема на [a;b], то она интегрируема на [a;c] и [c;b]. И тогда выполняются условия интегрируемости: . И т.к. f интегрируема на [a;b], то она интегрируема на [a;c] и [c;b]. И тогда выполняются условия интегрируемости:  тогда перейдя к пределу в равенстве (2) при условии тогда перейдя к пределу в равенстве (2) при условии  и в силу (1) получим (0). и в силу (1) получим (0). Однородность: Ф-ии f и g интегрируемы на [a;b]. 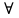 λ ∈ R и μ ∈ R, ф-я λ ∈ R и μ ∈ R, ф-я 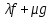 также интегрируема на этом отрезке и также интегрируема на этом отрезке и 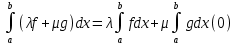 Д-во: ⊳ 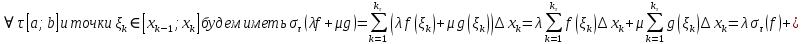 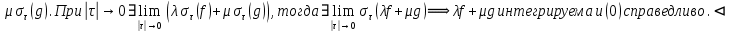 Неравенства: Ф-ии f и g интегрируемы на [a;b] и 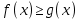 , x , x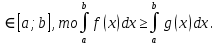 Д-во: ⊳Из 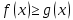 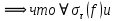 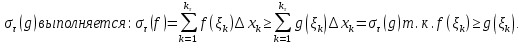 Перейдем к пределу при Перейдем к пределу при 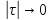 , получим , получим 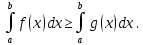 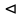 Теорема о среднем: Пусть на [a;b]: 1)f и g интегрируемы. 2) 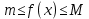 . .3)g не меняет знака. Тогда 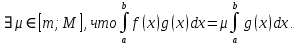 Д-во: ⊳ 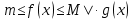 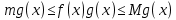 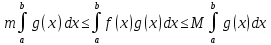 Если 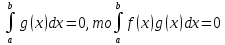 и и 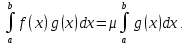 Если Если 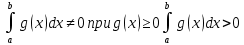 , а при , а при 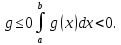 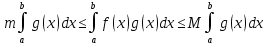 | : | : 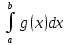 m 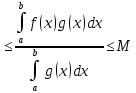 , пусть , пусть 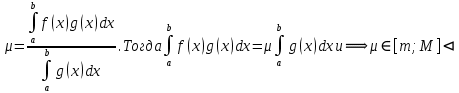 Следствие: Если  непрерывна на непрерывна на  и выполняется условие теоремы, то и выполняется условие теоремы, то 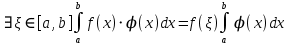 Д-во: Т.к. 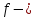 непрерывна на непрерывна на 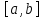 , то она достигает своего max и min значения, а в силу непрерывности sup=max, inf=min; значит , то она достигает своего max и min значения, а в силу непрерывности sup=max, inf=min; значит 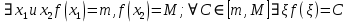 - по теореме о промежуточных значениях непрерывной функции. Следствие доказано. - по теореме о промежуточных значениях непрерывной функции. Следствие доказано.Следствие к следствию: Если 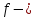 непрерывна на непрерывна на 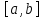 , то , то 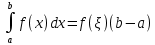 Д-во: Возьмем 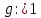 , тогда , тогда 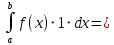 (по следствию) (по следствию) 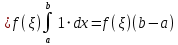 . Следствие доказано. . Следствие доказано.Геометрический смысл этого следствия: Если считать площадь криволинейной трапеции, то найдется такая точка 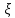 , что площадь этой криволинейной трапеции будет равна площади прямоугольника с высотой , что площадь этой криволинейной трапеции будет равна площади прямоугольника с высотой 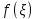 . .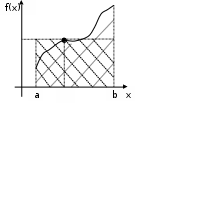 8. Интеграл как функция верхнего предела. Непрерывность. Рассмотрим функцию 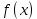 , интегрируемую на отрезке , интегрируемую на отрезке 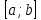 . По аддитивному свойству интеграла: . По аддитивному свойству интеграла: 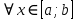 , можно найти отрезок , можно найти отрезок 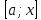 на котором представляется возможным рассмотреть функцию на котором представляется возможным рассмотреть функцию 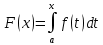 . .Теорема: Если функция 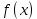 интегрируемая на отрезке интегрируемая на отрезке 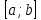 , то , то 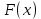 непрерывна на отрезке непрерывна на отрезке 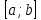 . .Доказательство: Рассмотрим функцию 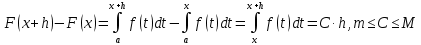 , где , где 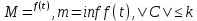 , где , где 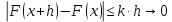 . Теорема доказана . Теорема доказана9. Дифференцируемость интеграла, как функции верхнего предела. Теорема Ньютона-Лейбница. Пусть f(x) – непр. на [a,b], значит она интегрируема, значит F(x). Тогда F(x) дифф-ма на (a,b) и 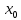 (a,b) F’( (a,b) F’(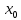 )=f )=f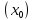 Д-во: 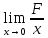 F= 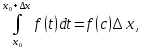 где c[ где c[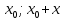 ] ( если x<0: c[ ] ( если x<0: c[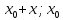 ]) ])При 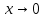 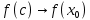 . Тогда . Тогда 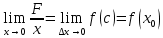 Следствие 1: Если 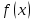 непр. на [a,b], то она имеет первообразную F(x) на [a,b]; непр. на [a,b], то она имеет первообразную F(x) на [a,b];Д-во: 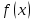 непр. на [a,b] F(x)= непр. на [a,b] F(x)=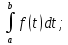 то для непр. то для непр. 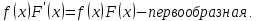 Следствие 2 (Ф-ла Ньютона-Лейбница): Если 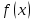 непр. на [a,b], то она интегрируема на [a,b] непр. на [a,b], то она интегрируема на [a,b] 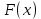 существует мн-во первообразных F(x). Пусть G(x) – произвольная п/о. Тогда справедливо: существует мн-во первообразных F(x). Пусть G(x) – произвольная п/о. Тогда справедливо: 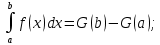 Пусть F(x)= 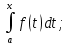 F(b)= F(b)=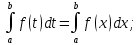 F(a)=0; F(a)-F(b)= 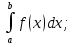 G(x)=F(x)+C G(b)-G(a)=F(b)-F(a)= G(x)=F(x)+C G(b)-G(a)=F(b)-F(a)=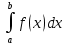 ; ;10. Несобственные интегралы. Определение. Виды. Сходимость. Критерий Коши. Опр: Пусть 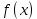 задана на луче задана на луче  и интегрируема на любом конечном отрезке и интегрируема на любом конечном отрезке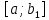 . Если существует предел . Если существует предел 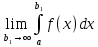 , то он называется несобственным интегралом первого рода и обозначается , то он называется несобственным интегралом первого рода и обозначается 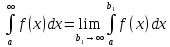 . .Опр: Пусть 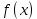 задана на полуинтервале задана на полуинтервале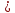 , интегрируема на любом конечном отрезке , интегрируема на любом конечном отрезке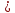 , ( , (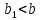 ) и неограниченна в окрестности точки ) и неограниченна в окрестности точки 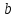 . Если существует предел . Если существует предел 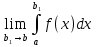 , то он называется несобственным интегралом второго рода и обозначается , то он называется несобственным интегралом второго рода и обозначается 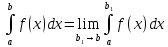 . .Если указанные пределы конечные, то интегралы называются сходящимися, если бесконечные, то расходящимися, если пределы не существуют, то, говорят, что несобственные интегралы не существуют. Теорема: (Критерий Коши сходимости несобственных интегралов) Пусть задан интеграл  с единственной особенностью в точке с единственной особенностью в точке  ( (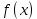 неограниченна в точке неограниченна в точке 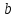 или или 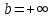 ). Для его сходимости необходимо и достаточно выполнения условия Коши: ). Для его сходимости необходимо и достаточно выполнения условия Коши: 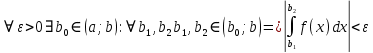 Д-во: Рассмотрим функцию 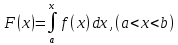 Тогда сходимость интеграла Тогда сходимость интеграла 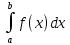 означает существование конечного предела функции означает существование конечного предела функции 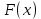 при при 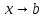 , а этот конечный предел, согласно Критерию Коши для функции , а этот конечный предел, согласно Критерию Коши для функции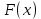 , существует в том и только том случае, когда , существует в том и только том случае, когда 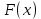 удовлетворяет условию: удовлетворяет условию: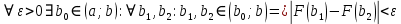 . . Но 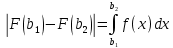 . Теорема доказана. . Теорема доказана. 11. Несобственные интегралы от неотрицательных функций. Признак сравнения, предельный признак сравнения, частный признак сравнения с интегралами 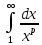 , ,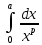 Теорема: Если 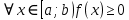 , то для сходимости , то для сходимости 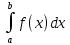 необходимо и достаточно, чтобы функция необходимо и достаточно, чтобы функция 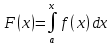 была ограничена сверху, т.е. была ограничена сверху, т.е. 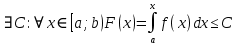 Д-во: Так как 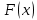 возрастающая функция, то из сходимости интеграла следует возрастающая функция, то из сходимости интеграла следует 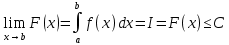 Обратно, если Обратно, если 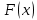 возрастающая функция и ограничена сверху, то она имеет конечный предел. Теорема доказана. возрастающая функция и ограничена сверху, то она имеет конечный предел. Теорема доказана.Теорема: (Признак сравнения). Если  выполняется условие выполняется условие  , тогда: , тогда:а) Из сходимости  следует сходимость следует сходимость 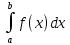 ; ;б) Из расходимости 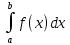 следует расходимость следует расходимость 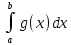 . .Д-во: а) Имеем 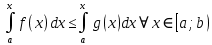 Так как Так как 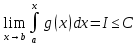 , то по предыдущей теореме , то по предыдущей теореме 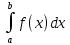 сходится. сходится.б) Из расходимости 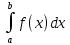 следует расходимость следует расходимость 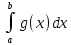 . Предположим обратное, что . Предположим обратное, что 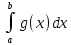 сходится, тогда по пункту а) сходится, тогда по пункту а) 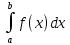 тоже сходится. Противоречие. Теорема доказана. тоже сходится. Противоречие. Теорема доказана.Теорема: (Предельный признак сравнения). Пусть функции 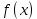 и и 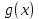 положительны и положительны и 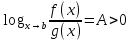 , тогда несобственные интегралы , тогда несобственные интегралы 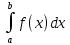 и и 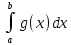 сходятся и расходятся одновременно. сходятся и расходятся одновременно.Д-во: 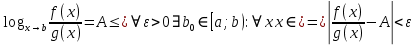 . Раскрывая последнее неравенство . Раскрывая последнее неравенство 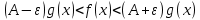 и используя признак сравнения, получим, что интегралы и используя признак сравнения, получим, что интегралы 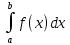 и и 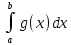 сходятся и расходятся одновременно. Теорема доказана. (Частный признак сравнения) Известно, что интеграл вида сходятся и расходятся одновременно. Теорема доказана. (Частный признак сравнения) Известно, что интеграл вида  сходится при р > 1 и расходится при р ≤ 1. Опираясь на теорему о предельном признаке сравнения, находим в подынтегральной функции разность старших степеней числителя и знаменателя и приходим к выводу, что интеграл необходимо сравнить с интегралом вида сходится при р > 1 и расходится при р ≤ 1. Опираясь на теорему о предельном признаке сравнения, находим в подынтегральной функции разность старших степеней числителя и знаменателя и приходим к выводу, что интеграл необходимо сравнить с интегралом вида 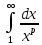 где р – найденная разность. Предел отношения подынтегральных функций должен оказаться конечным. На основе значения p делаем вывод о сходимости и расходимости. где р – найденная разность. Предел отношения подынтегральных функций должен оказаться конечным. На основе значения p делаем вывод о сходимости и расходимости.12. Абсолютно сходящиеся интегралы. Определение 1. Рассмотрим 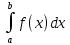 с единственной особенностью в точке с единственной особенностью в точке 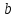 , конечной или бесконечной, тогда если , конечной или бесконечной, тогда если 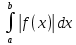 , у него, естественно, тоже единственная особенность в точке , у него, естественно, тоже единственная особенность в точке 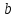 , сходящийся, то , сходящийся, то 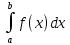 называется абсолютно сходящимся. называется абсолютно сходящимся.Теорема: если интеграл абсолютно сходится, то он сходится. Доказательство: Нам дано, что 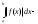 сходится. сходится.По критерию Коши  . Это уже наш обычный определенный интеграл Римана. Для него есть неравенство: . Это уже наш обычный определенный интеграл Римана. Для него есть неравенство: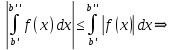 критерий Коши выполняется и для критерий Коши выполняется и для 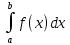 , то есть, по критерию Коши уже для нашего интеграла, он сходящийся. , то есть, по критерию Коши уже для нашего интеграла, он сходящийся.Кроме того, 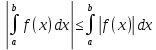 , тогда , тогда 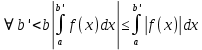 , переходя к пределу при , переходя к пределу при 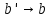 . Сразу мы такого сделать не могли, так как мы не знаем, существует ли этот предел слева или нет. Из того, что интеграл ограничен, существование предела еще не следует. Функция может быть не монотонна, поэтому мы и доказали сначала существование этого интеграла, а потом уже неравенство. . Сразу мы такого сделать не могли, так как мы не знаем, существует ли этот предел слева или нет. Из того, что интеграл ограничен, существование предела еще не следует. Функция может быть не монотонна, поэтому мы и доказали сначала существование этого интеграла, а потом уже неравенство.По признаку сравнения мы тоже так сделать не могли, так как он только для знакопостоянных функций. Определение 2. Если 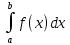 - сходящийся, а - сходящийся, а 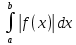 - расходящийся, то - расходящийся, то 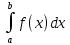 называется условно сходящимся. называется условно сходящимся.Когда мы исследуем интеграл от не знакопостоянной функции, мы должны сначала исследовать его сначала на абсолютную сходимость, если получится, что он абсолютно расходится, то надо исследовать на условную сходимость. Если он сразу абсолютно сходится, то все хорошо. Пример. Исследуем на абсолютную сходимость интеграл 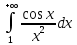 ; ;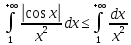 - сходящийся, значит и исходный интеграл сходящийся, то есть интеграл сходится абсолютно. Признаком сравнения мы сразу не имеем права пользоваться, потому что косинус у нас на этом промежутке может быть как положительным, так и отрицательным, поэтому мы исследуем интеграл на абсолютную сходимость - сходящийся, значит и исходный интеграл сходящийся, то есть интеграл сходится абсолютно. Признаком сравнения мы сразу не имеем права пользоваться, потому что косинус у нас на этом промежутке может быть как положительным, так и отрицательным, поэтому мы исследуем интеграл на абсолютную сходимость |
