Ответы. Модуль непрерывности функции одной переменной на множестве. Равномерная непрерывность
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
17. Предел функции нескольких переменных. Свойства. Предел по направлению. 1.Предел функции.  Определение1 (по Гейне): Пусть задана функция f из некоторого множества A→R ;A ⸦ Определение1 (по Гейне): Пусть задана функция f из некоторого множества A→R ;A ⸦ 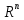 , точка , точка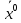 - внутренняя точка A, если - внутренняя точка A, если 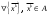 , , 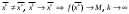 , то , то 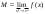 . .Определение: Окрестностью точки 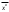 называется любое открытое множество, содержащее в себе некоторый открытый шар с центром в точке называется любое открытое множество, содержащее в себе некоторый открытый шар с центром в точке 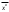 . .Определение2 (по Коши): 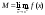 , если f определена в некоторой окрестности точки , если f определена в некоторой окрестности точки 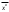 , , за исключением, быть может, самой точки 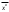 (в (в 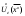 ), и выполняется условие ), и выполняется условие 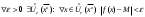 Определения по Коши и по Гейне эквивалентны, доказательство этого проводится аналогично доказательству для функций одной переменной. Теорема1 (критерий Коши существования предела функции): Существование конечного предела функции эквивалентно выполнению условия Коши: 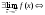 выполняется условие Коши: выполняется условие Коши: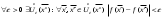 Доказательство аналогично случаю с одной переменной. 2.Свойства пределов функций многих переменных. Теорема1 (ограниченность сходящейся функции): Если функция 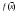 имеет конечный предел имеет конечный предел 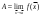 , где , где 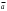 – конечное или бесконечное, то – конечное или бесконечное, то 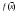 ограничена в некоторой выколотой окрестности точки ограничена в некоторой выколотой окрестности точки 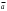 ( в ( в 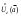 ). ).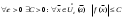 . .Теорема2 (о сохранении знака): Если функция 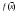 имеет конечный предел имеет конечный предел 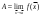 и и 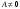 , а , а 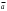 – конечное или бесконечное, то существует окрестность – конечное или бесконечное, то существует окрестность 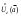 такая, что такая, что 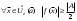 . Более того, . Более того, 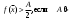 , и , и 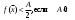 . .Теорема3 (предельный переход под знаком неравенства): Если 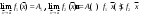 в некоторой выколотой окрестности в некоторой выколотой окрестности 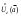 , то , то 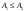 . .Теорема4: (лемма о двух милиционерах): Если 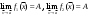 в некоторой выколотой окрестности в некоторой выколотой окрестности 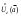 , и , и 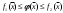 , то , то 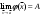 . .Теорема5: (арифметические свойства пределов): Пусть 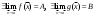 , где A и B – конечные, , где A и B – конечные, 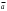 – конечное или бесконечное, то – конечное или бесконечное, то1. 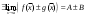 2. 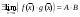 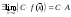 , где С – константа , где С – константа3. Если 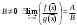  3.Пределы по направлениям. 3.Пределы по направлениям.Пусть задана функция 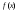 , определенная в некоторой , определенная в некоторой 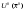 . .Рассмотрим произвольный вектор  , тогда, так как функция , тогда, так как функция 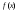 определена в некоторой окрестности точки определена в некоторой окрестности точки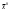 , она будет определена для всех точек вида , она будет определена для всех точек вида 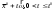 , тогда можно рассмотреть уже функцию одной переменной: , тогда можно рассмотреть уже функцию одной переменной: 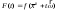 . И можно рассмотреть ее предел . И можно рассмотреть ее предел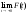 . Этот предел называется пределом функции . Этот предел называется пределом функции 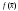 по направлению по направлению  . .  18. Непрерывность функции нескольких переменных. Непрерывность функции на замкнутом множестве. Определение: Функция f(x,y) непрерывна в точке (x0,y0) ,если она определена в некоторой её окрестности, в самой точке (x0,y0) и если предел f(x,y) в этой точке равен её значению в ней: 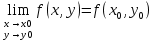 Эквивалентная форма: 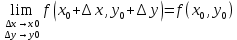 Если ввести приращение функции u=f(x,y) в точке (x,y), соответствующее приращениям аргументов, 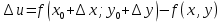 то функция непрерывна в точке (x,y), если 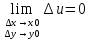 Определение: Точка x0 называется внутренней точкой множества G, если существует круг с центром в точке x0 , полностью принадлежащий множеству G. Определение: Точка x0 называется внешней точкой множества G, если существует шар с центром в точке x0 такой, что ни одна его точка не принадлежит множеству G. Определение: Точка x0 называется граничной точкой множества G, если существует шар с центром в точке x0 , содержащий точки принадлежащие множеству G и не принадлежащие множеству G. Множество называется открытым, если все его точки – внутренние. Множество G называется замкнутым, если оно содержит все свои предельные точки.    F(x) – непрерывна в граничной точке какого-то множества A. x0 – граничная точка : x0 F(x) – непрерывна в граничной точке какого-то множества A. x0 – граничная точка : x0 ꓯԐ>0 ∃δ>0 ꓯ 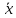 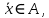 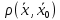 < δ -> | f( < δ -> | f(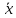 ) –f( ) –f(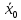 )|< Ԑ )|< ԐТеорема 1. Если f – непрерывна на А - замкнутое, ограниченное множество, то f ограничена на нем. Доказательство: Пусть 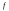 не ограничена на не ограничена на  , тогда , тогда 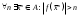 . .Множество  - ограниченное, следовательно, и последовательность - ограниченное, следовательно, и последовательность 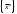 - ограниченная, значит, по теореме Больцано-Вейерштрасса из нее можно извлечь сходящуюся к - ограниченная, значит, по теореме Больцано-Вейерштрасса из нее можно извлечь сходящуюся к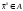 (в силу замкнутости) подпоследовательность (в силу замкнутости) подпоследовательность 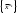 . Мы получаем, что . Мы получаем, что 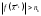 , а , а 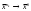 , значит , значит 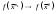 в силу непрерывности. Получили в силу непрерывности. Получили 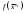 с одной стороны больше с одной стороны больше 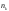 , а с другой стороны стремится к , а с другой стороны стремится к 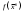 . Противоречие: . Противоречие: 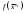 не может стремиться к конечному числу, потому что оно больше не может стремиться к конечному числу, потому что оно больше 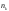 . Теорема доказана. . Теорема доказана.Теорема 2. Функция, непрерывная на замкнутом, ограниченном множестве, достигает своего максимального и минимального значения. Доказательство: Рассмотрим множество 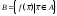 . Это множество по предыдущей теореме ограниченное, значит, существуют . Это множество по предыдущей теореме ограниченное, значит, существуют 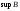 и и 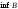 . .Рассмотрим случай максимума, для минимума все аналогично. Тогда по определению супремума 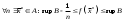 . .Из последовательности 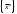 (ограниченной) выделяем сходящуюся (ограниченной) выделяем сходящуюся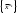 , , 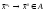 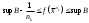 . Перейдем к пределам, так как . Перейдем к пределам, так как 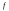 непрерывна, получим, что непрерывна, получим, что 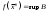 . . Теорема доказана. 19. Частные производные. Дифференцируемость функции нескольких переменных, дифференциал. Необходимые условия дифференцируемости. Частные производные. Пусть задана f( 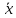 ) определена в некоторой окрестности точки ) определена в некоторой окрестности точки 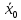 . .Зададим приращение h переменной xi так, чтобы точка попала в ( 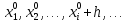 ). ).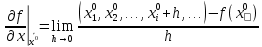 - частная производная. Частная производная есть обычная производная от функции, рассматриваемой как функция только от той переменной, по которой берется производная при фиксированных остальных переменных. - частная производная. Частная производная есть обычная производная от функции, рассматриваемой как функция только от той переменной, по которой берется производная при фиксированных остальных переменных.Если у функции 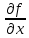 существует частная производная снова по x, то её называют частной производной второго порядка от функции f и обозначают существует частная производная снова по x, то её называют частной производной второго порядка от функции f и обозначают 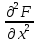 . .Если у функции 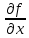 существует частная производная по y, то её называют смешанной частной производной второго порядка от функции f и обозначают существует частная производная по y, то её называют смешанной частной производной второго порядка от функции f и обозначают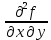 . . Дифференциал: Определение: Если приращение функции f в точке (x,y,z) для достаточно малых ( 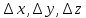 ) может быть записано в виде суммы ) может быть записано в виде суммы 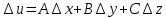 +o(p) p= +o(p) p=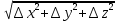 ,где A,B,C – числа не зависящие от ,где A,B,C – числа не зависящие от 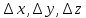 , то говорят, что функция f дифференцируема в точке (x,y,z). Т.е. приращение функции можно записать в виде суммы двух слагаемых : первое слагаемое есть линейная функция , то говорят, что функция f дифференцируема в точке (x,y,z). Т.е. приращение функции можно записать в виде суммы двух слагаемых : первое слагаемое есть линейная функция 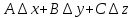 от от 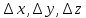 – главная линейная часть приращения – главная линейная часть приращения 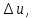 второе же слагаемое зависит от второе же слагаемое зависит от 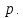 Теорема (достаточное условие дифференцируемости). Если функция 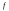 имеет непрерывные частные производные в точке имеет непрерывные частные производные в точке 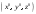 , то ее приращение представимо в виде: , то ее приращение представимо в виде:  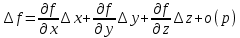 где частные производные вычислены в точке 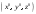 , т.е. не зависят от приращений. , т.е. не зависят от приращений.Доказательство: Пусть задана функцияf(x). Пусть в некоторой точке 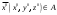 функция fимеет непрерывные частные производные функция fимеет непрерывные частные производные 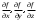 в некоторой окрестности точки в некоторой окрестности точки 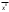 . Т.к. эти производные непрерывны в точке . Т.к. эти производные непрерывны в точке 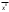 , это означает, что все они существуют в некоторой окрестности точки , это означает, что все они существуют в некоторой окрестности точки 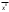 . Зададим приращения . Зададим приращения 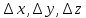 таким образом, чтобы точка с координатами таким образом, чтобы точка с координатами 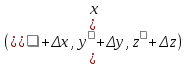 попала в ту окрестность, в которой функция имеет частные производные. попала в ту окрестность, в которой функция имеет частные производные.Рассмотрим приращение функции: 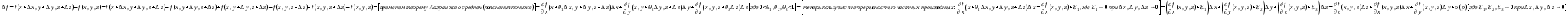 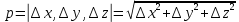 ,p->0 ,p->0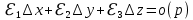 Т.к. 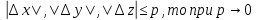 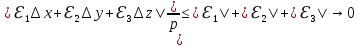 Чтд Пояснения: По теореме Лагранжа : 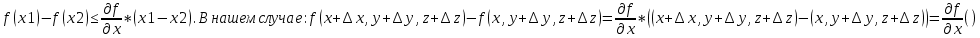 Теорема (необходимое условие дифференцируемости). Для того чтобы функция f была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные. Доказательство: Проведем теперь рассуждения в обратную сторону: пусть задана функция f, дифференцируемая в точке 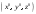 , тогда ее приращение представимо в виде: , тогда ее приращение представимо в виде: 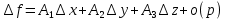 , где 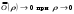 , в том числе по любому направлению. Возьмем в качестве приращения , в том числе по любому направлению. Возьмем в качестве приращения 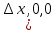 ) тогда p=| ) тогда p=|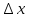 |->0 при |->0 при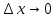 . .Тогда получим, что 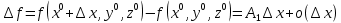 Разделим на 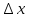 и устремим и устремим 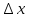 к нулю, получим: к нулю, получим: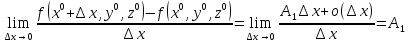 Слева – частная производная 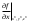 , справа - , справа - 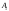 , т.е. , т.е. 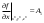 . .Таким образом, мы получили, что если функция дифференцируема в точке с координатами 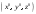 , то она имеет частные производные первого порядка и дифференциал , то она имеет частные производные первого порядка и дифференциал 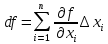 . .20. Дифференцируемые функции. Касательная плоскость. Рассмотрим частный случай, функцию трех переменных. Пусть задана функция f: 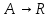 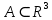 - открытое множество. Пусть в некоторой точке - открытое множество. Пусть в некоторой точке 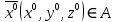 функция fимеет непрерывные частные производные функция fимеет непрерывные частные производные 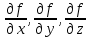 в некоторой окрестности точки в некоторой окрестности точки 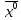 . Т.к. эти производные непрерывны в точке . Т.к. эти производные непрерывны в точке 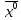 , это означает, что все они существуют в некоторой окрестности точки , это означает, что все они существуют в некоторой окрестности точки 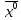 . Зададим приращения . Зададим приращения 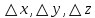 таким образом, чтобы точка с координатами таким образом, чтобы точка с координатами 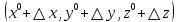 попала в ту окрестность, в которой функция имеет частные производные. попала в ту окрестность, в которой функция имеет частные производные.Рассмотрим приращение функции:  Теперь обозначим 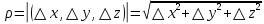 , тогда условие , тогда условие 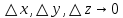 эквивалентно условию эквивалентно условию 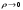 , потому что ранее было показано, что каждый куб содержится в шаре, каждый шар содержится в кубе, и условие , потому что ранее было показано, что каждый куб содержится в шаре, каждый шар содержится в кубе, и условие 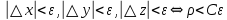 . .Докажем, что 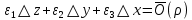 : :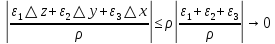 при при 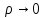 . . Доказано. Итак мы получили, что если функция 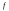 имеет непрерывные частные производные в точке имеет непрерывные частные производные в точке 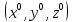 , то ее приращение представимо в виде: , то ее приращение представимо в виде: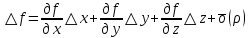 , где частные производные вычислены в точке , где частные производные вычислены в точке 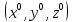 , т.е. не зависят от приращений. , т.е. не зависят от приращений.Определение: Если задана f: 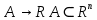 - открытое множество, точка - открытое множество, точка 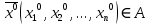 и если в этой точке приращение функции представимо в виде: и если в этой точке приращение функции представимо в виде: 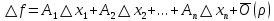 , где , где 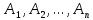 не зависят от приращений не зависят от приращений 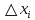 , то функция f называется дифференцируемой в точке , то функция f называется дифференцируемой в точке 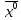 , а , а 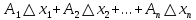 - дифференциал функции. Это главная линейная часть приращения функции. Линейная – потому что дифференциал линейно зависит от приращения аргумента, главная – потому что то, на что дифференциал отличается от приращения функции, имеет больший порядок малости. - дифференциал функции. Это главная линейная часть приращения функции. Линейная – потому что дифференциал линейно зависит от приращения аргумента, главная – потому что то, на что дифференциал отличается от приращения функции, имеет больший порядок малости.Итак, мы доказали для случая 3-х переменных (для случая n переменных доказывается точно так же, только более громоздко), что если f имеет непрерывные частные производные, то она дифференцируема и 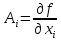 . Кроме того, дифференциал можно рассматривать как линейный оператор: . Кроме того, дифференциал можно рассматривать как линейный оператор:возьмем в качестве A вектор 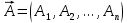 , то , то 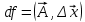 , где , где 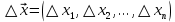 . .Проведем теперь рассуждения в обратную сторону: пусть задана функция f, дифференцируемая в точке 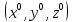 , тогда ее приращение представимо в виде: , тогда ее приращение представимо в виде: 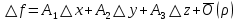 , где , где 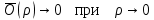 , в том числе по любому направлению. Возьмем в качестве приращения , в том числе по любому направлению. Возьмем в качестве приращения 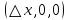 , тогда , тогда 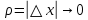 при при 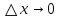 . .Получим, что 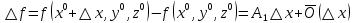 Разделим на 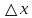 и устремим и устремим 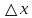 к нулю, получим: к нулю, получим: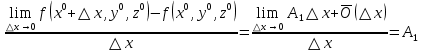 Слева – частная производная 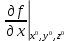 , справа - , справа - 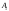 , т.е. , т.е. 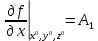 . .Таким образом, мы получили, что если функция дифференцируема в точке с координатами 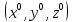 , то она имеет частные производные первого порядка и дифференциал , то она имеет частные производные первого порядка и дифференциал 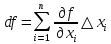 . .Мы доказали общую теорему: Теорема (необходимое и достаточное условия дифференцируемости): Необходимое условие: если функция f дифференцируема в точке 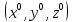 , то она имеет частные производные. , то она имеет частные производные.Достаточное условие: если существуют непрерывные частные производные, то функция f дифференцируема. Таким образом, получается следующая цепочка: непрерывность ч.п.  функция дифференцируема функция дифференцируема  существуют частные производные существуют частные производныеНи в том, ни в другом месте стрелку в обратную сторону поставить нельзя, т.е. необходимое условие не является достаточным, достаточное не является необходимым. |
