отчет. Н. Ф. Гусарова, Н. В
 Скачать 2.27 Mb. Скачать 2.27 Mb.
|
«4», «4», «4», «4», «4»   Рис. 4.6. Результаты распознавания символа «8», искаженного 10% шума «Соль и Перец», результат распознавания (слева направо): «8», «8», «6»Результаты распознавания символов, представленные на рисунках 4.2-4.6, демонстрируют хорошее распознавание с помощью НС даже при сильном искажении (параметр p>0,1). Для объективной оценки ка- чества работы НС необходимо вычисление вероятностных характеристик распознавания. При правильном выборе параметров обучения сети и ис- пользовании не менее 100 обучающих образов можно получить вероятность правильного распознавания символов порядка 0,6…0,9 (в зависимости от вида распознаваемого символа) при параметре искажения p=0,1…0,2. Качество работы НС характеризуется вероятностями правильной клас- сификации образа i-го класса, i=1,…,M. Оценка вероятностей произво- дится по формуле:  пр P ˆ (i) NпрN0 , где Nпр число правильных распознаваний образа i-го класса; N0 - общее число распознаваний образов i-го класса. Число определяется экспериментально при запуске программы sr_work при значениях =10…100. ЦЕЛЬ РАБОТЫИсследование возможностей распознавания печатных символов с помощью нейронных сетей, а также построение нейронных сетей в среде MATLAB. ЗАДАНИЕ НА ПРАКТИЧЕСКУЮ РАБОТУ И ПОРЯДОК ВЫПОЛНЕНИЯПодготовить графические файлы эталонных образов для симво- лов, заданных преподавателем, или самостоятельная подготовка эталонных (обучающих) образов печатных символов в виде набора графических фай- лов. В среде MATLAB создать и обучить нейронную сеть (НС), пред- назначенную для распознавания печатных символов. Исследовать зависимость качества работы НС от: степени искажения символов (параметр p); числа нейронов в скрытом слое. ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫЦель работы: обучить нейронную сеть распознавать рукописные цифры. Перед нами стоит задача классификации: есть десять эталонных об- разцов, цифры от 0 до 9. Импорт библиотек для работы и загрузка датасета MNIST. MNIST - объёмная датасет образцов рукописного написания цифр. Он вклю- чает в себя 60,000 изображений для тренировки and 10,000 тестовых изоб- ражений.  Части x_train и x_test содержат изображения в цветовом про- странстве RGB в оттенках серого (уровни яркости от 0 до 255). Выведем пример рукописной цифры из датасета MNIST. 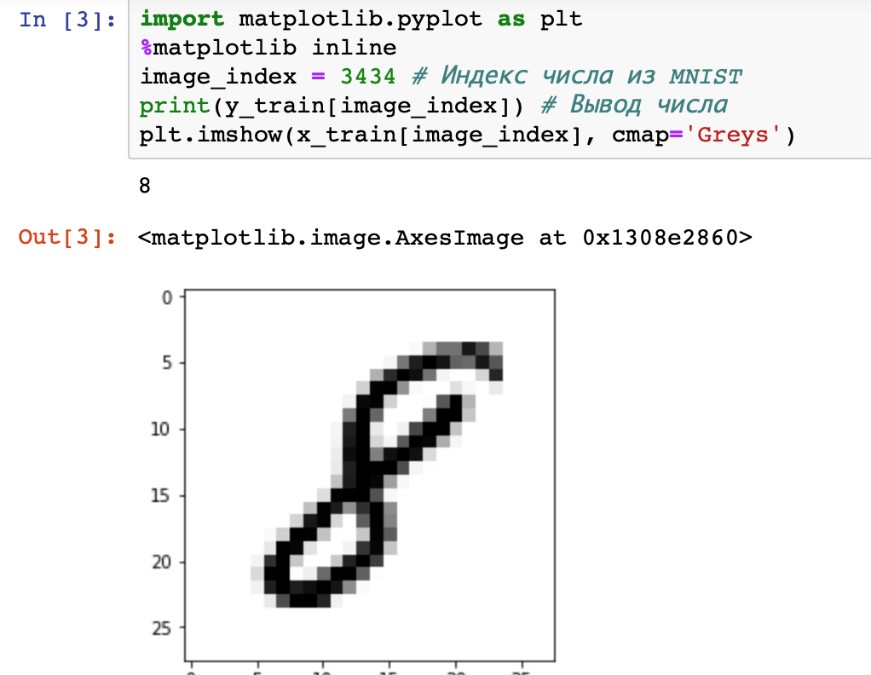 Тренировочная выборка: 60000 изображений 28*28 пикселей. Тестовая выборка: 10000 изображений 28*28 пикселей.  Нормализация изображений. Мы должны нормализовать наши данные, как это всегда требуется в моделях нейронных сетей. Мы можем достичь этого, разделив коды RGB на 255 (это максимальное значение для цветового пространства RGB). Преобразуем данные в float. Теперь уровень яркости определяется значением от 0 до 1.  Построение нейронной сети. Мы будем конфигурировать нашу сеть с помощью Kernas API с использованием библиотеки TensorFlow, кото- рая включает инструменты для работы с сетью. Входные значения: 784 (28*28) значений от 0 до 255 (уровней яркости изображения) На входной слой – 800 нейронов. На выходной слой 10 нейро- нов и вероятность что на изображении эталонная цифра. Используется последовательная модель: модель, в которой слои нейронной сети идут друг за другом.   Компиляция. Метод обучения – Adam adaptive moment estima- tion. Он сочетает в себе и идею накопления движения и идею более слабого обновления весов для типичных признаков. Компиляция. Метод обучения – Adam adaptive moment estima- tion. Он сочетает в себе и идею накопления движения и идею более слабого обновления весов для типичных признаков.Запуск (10 эпох) и определение точности.  Точность модели после сравнения составила 98%.  Проверим индивидуальное распознавание цифр. 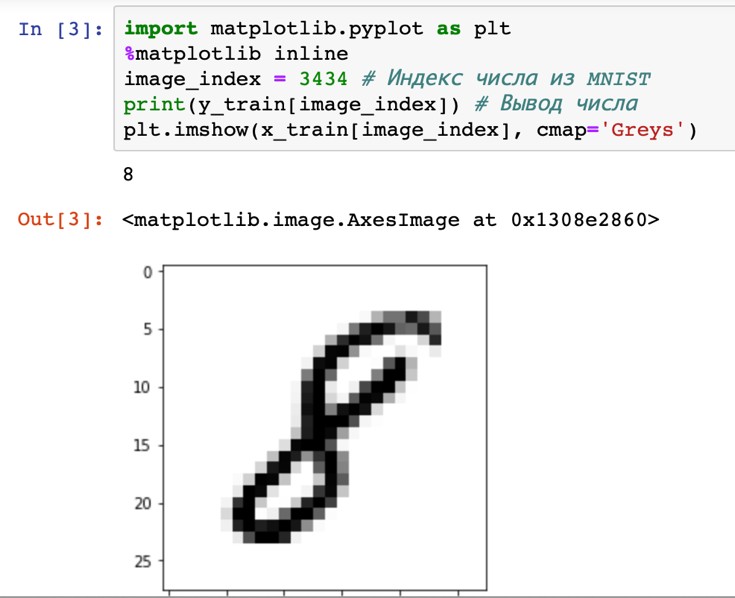 Проверим сеть, как она будет работать с искаженными циф- рами. Для этого с помощью Adobe Photoshop создаем изображение размером 32*32 и рисуем цифру. Для более оптимизированной работе тестовое изоб- ражение сохраняется в формате .tif.  Нормализация изображения для теста. Нормализация изображения для теста.Без искажений. 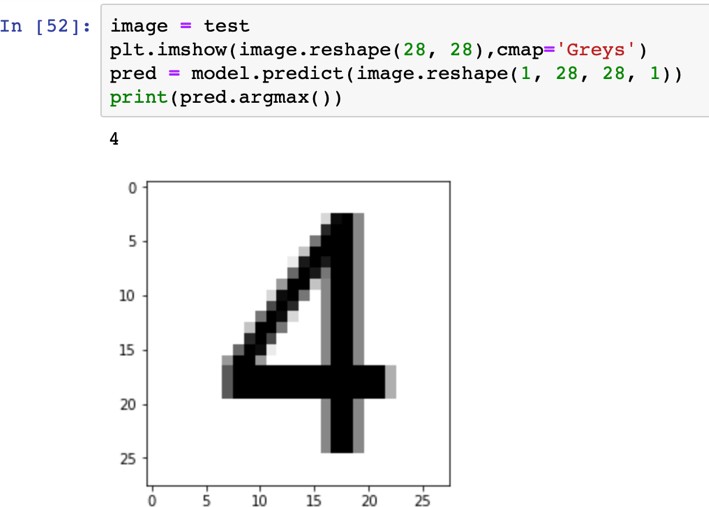 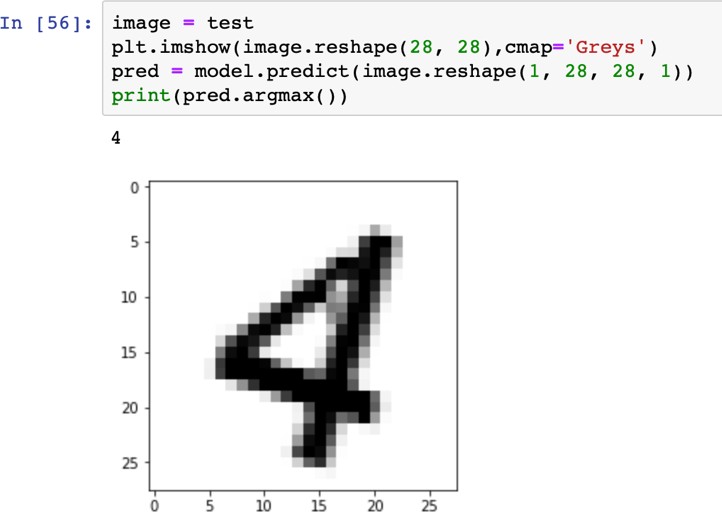 Фильтр «diffusion» 10% + поворот вправо на 20*. Фильтр «diffusion» 10% + поворот вправо на 20*.Фильтр «diffusion» 20%. 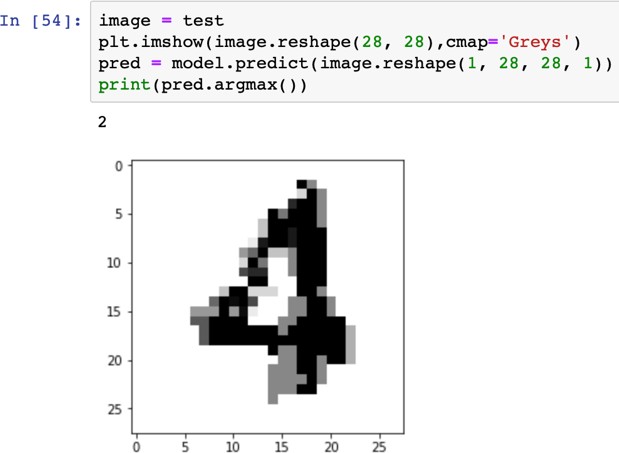 Фильтр «diffusion» 15%, масштабирование, лишний элемент, пово- рот. 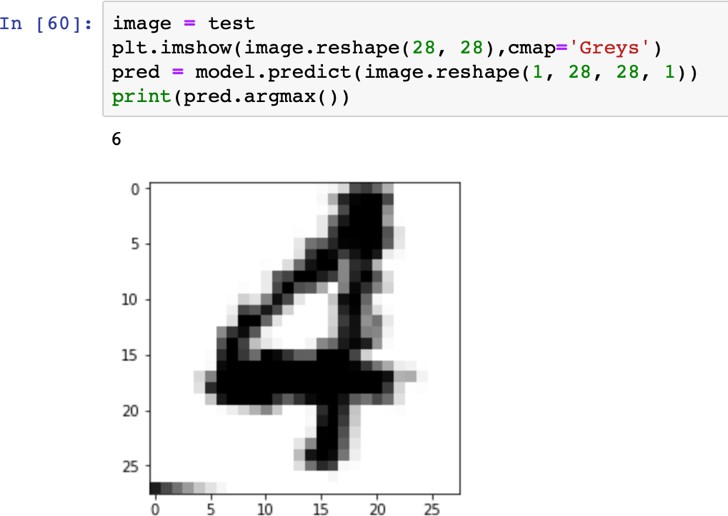  Попробуем другую цифру. Без искажений. Попробуем другую цифру. Без искажений.Поворот на 30%. 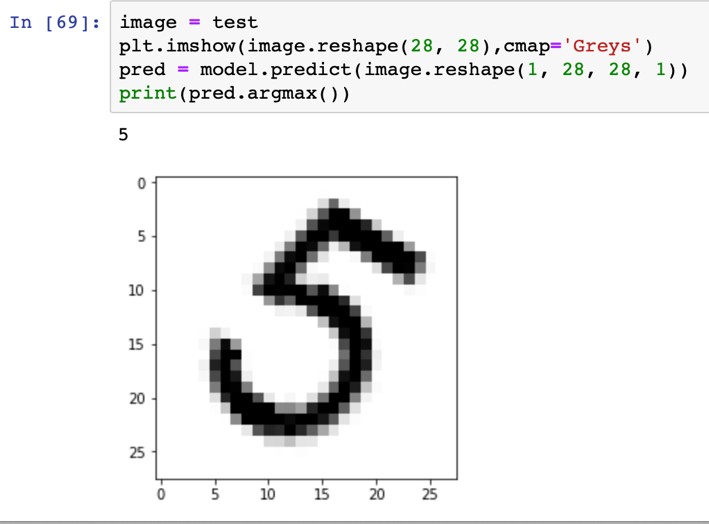 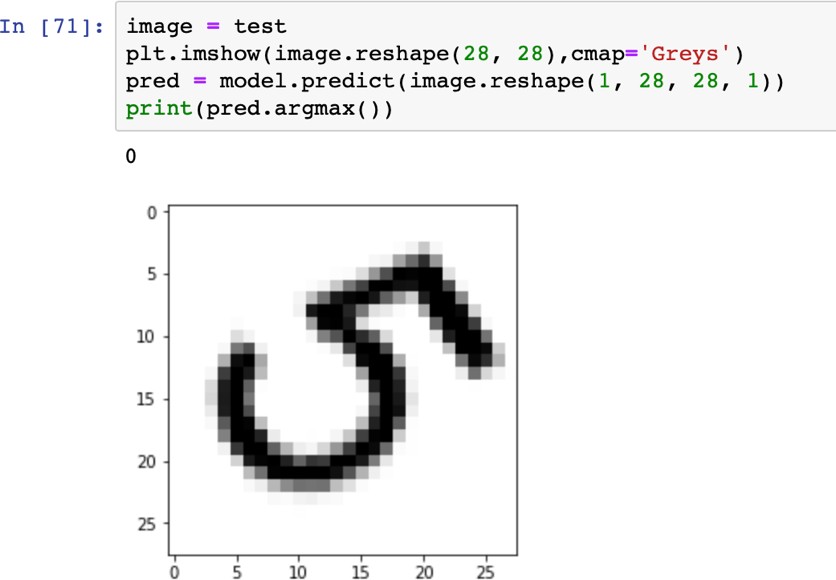 Поворот на 40%. Поворот на 40%.Фильтр «diffusion» 10%. 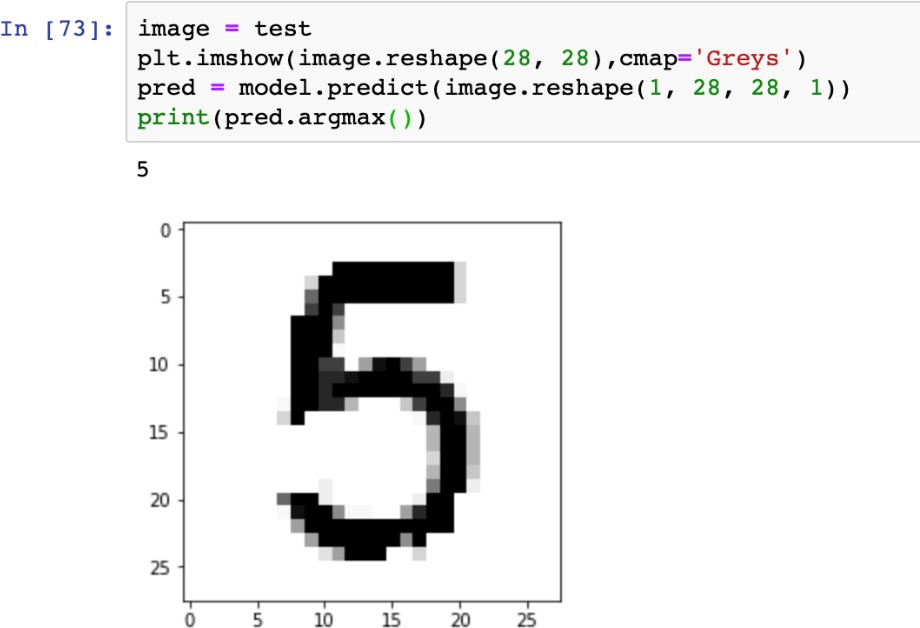 Фильтр «diffusion» 30%. 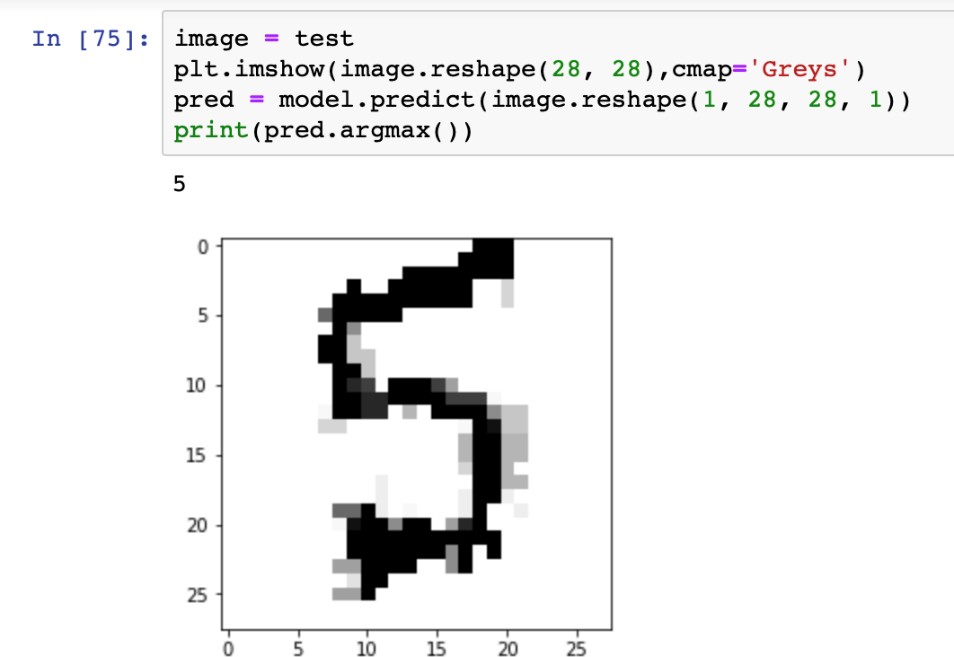 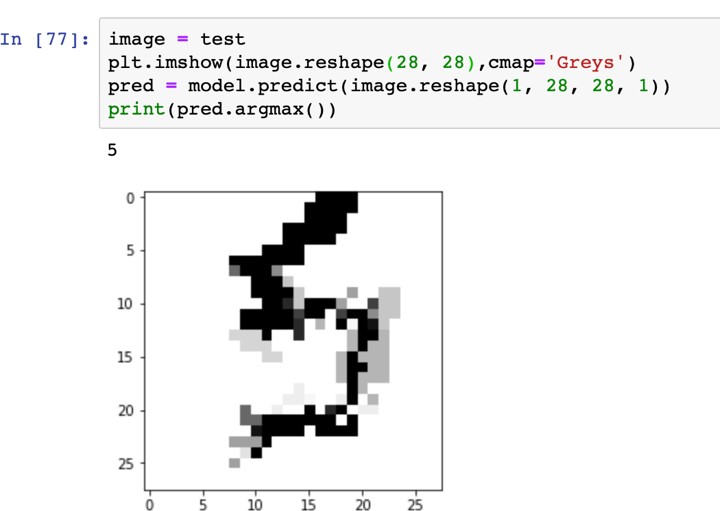 Фильтр «diffusion» 50%. Фильтр «diffusion» 50%. |
