отчет. Н. Ф. Гусарова, Н. В

• Название: Н. Ф. Гусарова, Н. В
• Анкор: отчет
• Дата: 19.02.2022
• Размер: 2.27 Mb.
• Имя файла: 2536.docx
• Тип: Документы; #367348
• страница: 9 из 19

Вход: U – обучающая выборка; B – множество элементарных предикатов;

Выход: возвращает корневую вершину дерева, построенного по выборке U;

1: ПРОЦЕДУРА LearnID3 (U);

2: если все объекты из U лежат в одном классе c ∈ Y

то

3: создать новый лист v; ^{4: c}v ^{:= c;}

5: вернуть (v);

6: найти предикат с максимальной информативностью: β := arg max I(β, U); β∈B

^{7: разбить выборку на две части U = U}0^𝖴U1 ^{по предикату} β:

^U0 ^{:= {x ∈ U : β(x) = 0};}

U1 := {x ∈ U : β(x) = 1};

8: если U0 =  или U1 =  то

9: создать новый лист v;

^{10: c}v ^{:= класс, в котором находится большинство объ-} ектов из U;

11: иначе

12: создать новую внутреннюю вершину v; ^{13: β}v ^{:= β;
14: L}v ^{:= LearnID3 (U}0^{); (построить левое поддерево) 15: Rv := LearnID3 (U}1^{); (построить правое поддерево)} 16: вернуть (v);
Проблемы, возникающие при реализации алгоритма:

П1. Как определить информативность предиката? – 2 варианта. Точный критерий Фишера основан на вычислении вероятности реа-

лизации пары событий: информативность предиката (x), разделяющего со- бытия правильного обнаружения p_cнужных объектов и правильного необ- наружения N_cненужных объектов, относительно класса c ∈ Y по выборке _Xℓ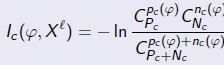

^.

в случае произвольного числа классов Y = {1, . . . ,M}

I(, X^l

C^p1...C^pM


C

_{)  } P1 PM_ln
p

l

(*)

где P_c - число объектов класса c в выборке X^ℓ, из них p_c объектов выделяются предикатом , p = p1+…+ pM.

Энтропийный = информационный критерий основан на сравнении энтропии (математического ожидания количества информации) о выборке до и после применения предиката . Если в выборке есть P объектов класса с и N остальных, то ее энтропия равна

⁾ P P N N _.




H(P, N)   _{P N}log_{2 P N} _{P N}log_{2 P N}

Если предикат  выделил p объектов из P, принадлежащих классу c, и n объ- ектов из N, не принадлежащих классу c, то энтропия выборки после получе- ния этой информации стала равной

⁾ p n⁾

P N p n ⁾ _.

H_ (P, N, p, n)  _{P N}H( p, n) 

P N

H(P p, N n)

Тогда энтропийный = информационный критерий для двух классов вво- дится как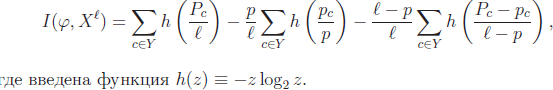

IGain(, X^l )  H(P, N)  H(P, p, N, n)^, а для большого числа классов – как

(**)

П2. На шаге 6 Алгоритма 2 выбирается предикат β из заданного се- мейства B, задающий максимально информативное ветвление дерева – раз- биение выборки на две части U = U₀ 𝖴 U₁.

На практике применяются различные критерии ветвления.

1. 
   Критерий, ориентированный на отделение заданного класса c ∈ Y . I(β, U) = max I_c(β, U), c∈Y.
   
2. 
   Критерии, ориентированные на отделение сразу нескольких классов – (*) и (**).
   
3. 
   D-критерий _ число пар объектов из разных классов, на которых предикат β принимает разные значения. В случае двух классов он имеет вид
   

I(β, U) = p(β)(N − n(β))+ n(β)(P − p(β)).

Другие варианты критериев можно найти в [2].

П3. Как выбрать условия деления выборки в каждом узле?

На практике в качестве элементарных предикатов чаще всего берут простые пороговые условия вида β(x) = [fj(x) >< dj]. Конъюнкции, состав- ленные из таких термов, хорошо интерпретируются и допускают запись на естественном языке. Однако никто не запрещает использовать в вершинах дерева любые разделяющие правила: шары, гиперплоскости, и, вообще го- воря, произвольные бинарные классификаторы. Когда мощность |B| не ве- лика, эта задача решается полным перебором, дальше нужны эвристики.

П4. Как удалить поддеревья, имеющие недостаточную статистиче- скую надёжность? = проблема редукции решающих деревьев.

Наиболее распространенные эвристики:

Предредукция (pre-pruning) или критерий раннего останова досрочно прекращает дальнейшее ветвление в вершине дерева, если информатив- ность I(β, U) для всех предикатов β ∈ B ниже заданного порогового значения I₀. Для этого на шаге 8 условие (U0 =  или U1 = ) заменяется условием I(β, U)  I₀. Порог I₀ является управляющим параметром метода.

Постредукция (post-pruning) просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех пор, пока в дереве остаются вершины, удовле- творяющие критерию замены. Критерием замены является сокращение числа ошибок на контрольной выборке, отобранной заранее, и не участво- вавшей в обучении дерева. Стандартная рекомендация - оставлять в кон- троле около 30% объектов.

Для реализации постредукции контрольная выборка Xk пропуска- ется через построенное дерево. При этом в каждой внутренней вершине v запоминается подмножество S_v ⊆ X_k попавших в неё контрольных объектов. Если Sv = , то вершина v считается ненадёжной и заменяется терминаль- ной по мажоритарному правилу: в качестве c_v берётся тот класс, объектов которого больше всего в обучающей подвыборке U, пришедшей в вершину

v. Затем для каждой внутренней вершины v вычисляется число ошибок, по- лученных при классификации выборки Sv следующими способами:

1. 
   r(v) - классификация поддеревом, растущим из вершины v;
   
2. 
   r_L(v) - классификация поддеревом левой дочерней вершины L_v;
   
3. 
   r_R(v) - классификация поддеревом правой дочерней вершины R_v;
   
4. 
   r_c(v) - отнесение всех объектов выборки S_v к классу c ∈ Y .
   

Эти величины сравниваются, и, в зависимости от того, какая из них оказалась минимальной, принимается, соответственно, одно из четырёх ре- шений:

1. 
   сохранить поддерево вершины v;
   
2. 
   заменить поддерево вершины v поддеревом левой дочерней вершины Lv;
   
3. 
   заменить поддерево вершины v поддеревом правой дочерней вершины Rv;
   
4. 
   заменить поддерево v терминальной вершиной класса c = arg min r_c(v). c∈Y.
   

Предпросмотр (look ahead) заключается в том, чтобы на шаге 6, вме- сто вычисления информативности для каждого β ∈ B построить поддерево небольшой глубины h. Во внутреннюю вершину v помещается тот предикат β, при котором поддерево допускает наименьшее число ошибок. Этот алго- ритм работает заметно дольше, но строит более надёжные и простые

деревья. Более подробно со спецификой применения методов можно озна- комиться в [8].