отчет. Н. Ф. Гусарова, Н. В

• Название: Н. Ф. Гусарова, Н. В
• Анкор: отчет
• Дата: 19.02.2022
• Размер: 2.27 Mb.
• Имя файла: 2536.docx
• Тип: Документы; #367348
• страница: 8 из 19

Выводы

Сравнив результаты двух методов отбора признаков (линейная ре- грессия и случайный лес), мы получили схожие результаты. Оба метода ука- зывают на важность признаков Glucose и Resistin, но точность метода Ran- dom Forest больше, чем метода Линейной регрессии. В данном случае, учи- тывая специфику выборки, имеет смысл брать выявленные признаки в рас- смотрение. Подводя итог, было отобрано 2 признака из девяти рассматрива- емых. Сокращение числа признаков увеличит скорость обработки данных и качество результатов, так как малоинформативные признаки будут отбро- шены.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Что такое нормализация данных?
   
2. 
   Перечислите основных преимущества отбора признаков?
   
3. 
   В чем основная идея отбора признаков с помощью генетического алго- ритма?
   
4. 
   В чём отличия внутренних и внешних критериев?
   

ПРАКТИЧЕСКАЯ РАБОТА №3.

ДЕРЕВЬЯРЕШЕНИЙ

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ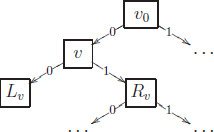

Бинарное решающее дерево – это алгоритм классификации, задаю- щийся бинарным деревом, в котором каждой внутренней вершине v ∈ V при- писан предикат β_v : X → {0, 1}, каждой терминальной вершине v ∈ V припи- сано имя класса c_v ∈ Y . При классификации объекта x ∈ X он проходит по дереву путь от корня до некоторого листа, в соответствии с Алгоритмом 1.

Алгоритм 1. Классификация объекта x ∈ X бинарным решающим деревом

1: v := v0;

2: пока вершина v внутренняя ^{3: если β}v^{(x) = 1 то}

^{4: v := R}v^{; (переход вправо)} 5: иначе

^{6: v := L}v^{; (переход влево) 7: вернуть c}v^.

Объект x доходит до вершины v тогда и только тогда, когда выпол- няется конъюнкция K_v(x), составленная из всех предикатов, приписанных внутренним вершинам дерева на пути от корня v₀ до вершины v. Естествен- ное требование максимизации информативности конъюнкций K_v(x) озна- чает, что каждая из них должна выделять как можно больше обучающих объектов, допуская при этом как можно меньше ошибок. Задача построения дерева минимальной сложности, правильно классифицирующего заданную выборку, в общем случае является NP-полной задачей. На практике приме- няют различные эвристики.

В данной практической работе рассматривается алгоритм 2 построе- ния решающего дерева ID3 (Induction of Decision Tree). Идея алгоритма за- ключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Алгоритм записывается в виде рекурсивной процедуры LearnID3, которая строит де- рево по заданной подвыборке U. Для построения полного дерева она приме- няется ко всей выборке и возвращает указатель на корень построенного де- рева:

v0 := LearnID3 (Xℓ).

Алгоритм 2. Рекурсивный алгоритм синтеза бинарного решающего дерева

ID3