Статистика. На основе данных, приведенных в таблице 1, выполнить

• Название: На основе данных, приведенных в таблице 1, выполнить
• Анкор: Статистика
• Дата: 09.02.2021
• Размер: 140.38 Kb.
• Имя файла: Statistika_Shurygina_A_SPEbz-118.docx
• Тип: Документы; #175230
• страница: 2 из 3

Задание №2.

1. На основе равноинтервальной структурной группировки (для любого признака) построить вариационный частотный и кумулятивный ряды распределения, оформить в таблице, изобразить графически.

2. Проанализировать вариационный ряд распределения, вычислив:

- среднее арифметическое значение признака;

- медиану и моду, квартили и децили (первую и девятую) распределения;

- среднее квадратичное отклонение;

- дисперсию;

- коэффициент вариации.

3. Сделать выводы.

Решение.

На основе структурной группировки построим таблицу:

Таблица 2.1

Вариационное распределение предприятий по размеру начисленных дивидендов

Границы интервалов	Частота, N_i	Середина интервала, x_i	Относительная частота, N_i/Δ	Накопленная частота,∑N_i
17 - 17,63	3	17,32	4,80	3
17,63 - 18,26	4	17,95	3,20	5
18,26 - 18,89	8	18,58	12,80	13
18,89 - 19,52	8	19,21	16,00	23
19,52 - 20,15	9	19,84	14,40	32
20,15 - 20,78	6	20,47	8,00	37
20,78 - 21,41	10	21,10	17,60	48
21,41 - 22,04	2	21,73	3,20	50

x_i=(𝑥𝑚𝑖𝑛+ 𝑥𝑚𝑎𝑥)/2 = (17+17,63)/2 = 17,32

N_i/∆ = N_i / Δ𝑖 = 3/0,63 = 4,8

∑N_i= N_i+ N_i+1 = 3 + 0 = 3, далее 3 + 2 = 5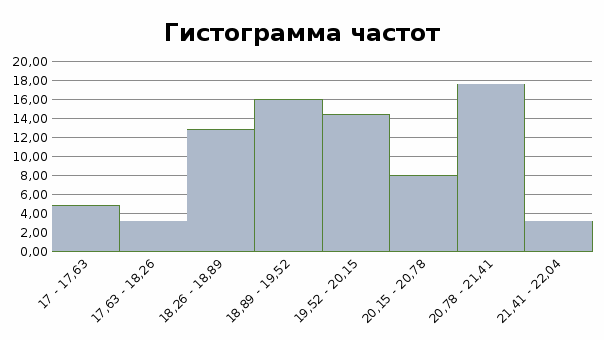



Рис.2.1. Гистограмма распределения предприятий по начисленным дивидендам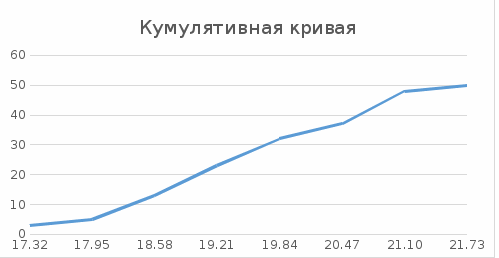



Рис.2.2. Кумулята распределения предприятий по начисленным дивидендам

С 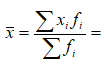реднее значение определим по формуле средней арифметической взвешенной, в качестве варианта используя середин интервалов 984,8/50 = 19,70 руб.

Найдем моду, для этого сначала найдем модальный интервал, т.е. интервал с наибольшей частотой. Чтобы найти конкретное значение моды, необходимо использовать формулу



где x_Мо - нижняя граница модального интервала; i_Мо - величина модального интервала; f_Мо - частота модального интервала; f_Мо-1 - частота интервала, предшествующего модальному; f_Мо+1 - частота интервала, следующего за модальным.

млн. руб.

Найдем медиану, для этого сначала найдем медианный интервал, т.е. первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. Численное значение медианы обычно определяют по формуле



где: 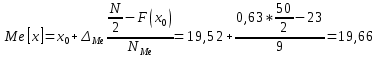- нижняя граница модального интервала;

- величина модального интервала;

- накопленная частота интервала, предшествующего медианному;

- частота медианного интервала;

млн.руб.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль первого порядка (нижний квартиль) и квартиль третьего порядка (верхний квартиль). Каждый из них отсекает соответственно ¼ и ¾ совокупности. Для расчета квартилей используются следующие формулы: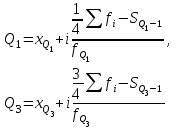



- нижняя граница интервала, содержащего нижний квартиль. Интервал определяется по сумме накопленных частот, превышающих 25 %

- нижняя граница интервала, содержащего верхний квартиль. Интервал определяется по сумме накопленных частот, превышающих 75 %

- шаг интервала

- накопленные частоты интервала, предшествующего интервалу, содержащему нижний квартиль

- накопленные частоты интервала, предшествующего интервалу, содержащему верхний квартиль

- частота интервала, содержащего нижний квартиль

- частота интервала, содержащего верхний квартиль

𝑄1 =𝑥0+𝛥𝑄𝑖𝑖∗𝑁/4−𝐹(𝑥0)𝑁𝑄𝑖 = 18,26+0,63*(50/4-5)/8 = 18,85 млн руб.

𝑄3 =𝑥0+𝛥𝑄𝑖𝑖∗𝑁/4−𝐹(𝑥0)𝑁𝑄𝑖 = 20,15+0,63*(50/4*3-32)/5 = 20,84 млн руб.

Определим показатели степени вариации.

Найдем дисперсию

= 19 465,9/50 = 389,32

= 382,32 – 19,7ˆ2 = 1,37
Найдем среднее квадратическое отклонение

= √1,37= 1,17

Найдем коэффициент вариации

= 1,17/19,7*100=5,94

Определим децили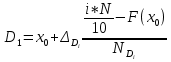

= 17,63+0,63*(50/10-3)/2 = 18,26

20,8+0,625*(9*50/10-37)/11 = 21,24,

Задание №3

1. Пользуясь таблицами №2 и №3, сформировать таблицу исходных данных.

2. Определить индивидуальные индексы:  физического объема,  цены;  стоимости.

3. Определить общие индексы:

 физического объема,  цены;

 стоимости, как агрегатные и как средние из индивидуальных.

Объяснить экономический смысл каждого из индексов, показать взаимосвязь между ними.

4. Определить абсолютное изменение стоимости произведенной продукции в текущем периоде по сравнению с базисным, в том числе, за счет изменения цен и за счет изменения выпуска продукции.

5. Считая продукцию однородной, определить как изменилась средняя цена единицы продукции и как при этом повлияло изменение цен и изменение структуры выпускаемой продукции. Объяснить полученные результаты.
Показатели выпуска продукции

			Вид продукции (варианты)
			I		II		III
Базисный период	Выпуск продук- ции, тыс.шт.	66		56		63
	Цена за единицу, тыс.руб./шт.	44		60		18
Текущий период	Выпуск продук- ции, тыс.шт.	56		76		35
	Цена за единицу, тыс.руб./шт.	31		15		19

Расчет



Индивидуальные индексы:

физический объем работ или услуг

цена

стоимость

Общие индексы:
Первый подход: на основе индексных формул
I_p^П =	Ʃ(p_1* q_1)/Ʃ(p_0*q_1) = 3 541 000 / 7 654 000 =					0,462634
I_q^Л =	Ʃ(p_0* q_1)/Ʃ(p_0*q_0) = 1,034604
I_pq =	Ʃ(p_1* q_1)/Ʃ(p_0*q_0) = 0,478643
Связь индексов
I_p^П*I_q^Л=		0,462634 * 1,034604 = 0,478643

Второй подход: на основе усреднения индексов
I_p= (Ʃ(p_1 * q_1))/(Ʃp_1 * q_1 / i_p) = 3 541 000 / 7 654 000 = 0,724346
I_q= (Ʃ(i_q * p_0 * q_0))/(Ʃp_0 * q_0) = 7 654 000/ 7 398 000 = 1,034604
I_p * I_q = 0,462634 * 1,034604 = 0, 478643