методика математики книга. Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
|
§42. Розвиток умінь учнів розв'язувати складені задачі Формування й розвиток умінь в учнів початкових класів розв'язувати задачі забезпечуються дотриманням загальних методичних вимог у роботі над задачами, а також деякими спеціальними прийомами, що конкретизують і доповнюють загальнометодичні настанови. Уміння розв'язувати задачу передбачає знання тих загальних правил, які сприяють раціональному підходу до пошуків розв'язання. У широкому розумінні розв'язування задачі розпочинається зі збирання необхідної інформації. Вивчають задачну ситуацію, запитання задачі, згадують або знаходять з певних джерел ті ознаки й властивості величин, про які йдеться в задачі. Потім з'ясовують залежності між даними і шуканими величинами, а також ознаки і властивості, які слід використовувати для знаходження відповіді на запитання. На основі цього визначають хід розв'язування. Це конструктивна (і основна) частина роботи над задачею. Друга частина — виконавча, коли роблять необхідні записи; визначають дії чи складають вираз або рівняння; здійснюють обчислення і записи відповіді; перевіряють розв'язання. У навчанні учнів початкових класів цей порядок роботи подається у вигляді порад, що формулюються в інструкції (пам'ятці). Дає позитивні результати така система порад: а) уважно прочитай задачу; подумай, про що йдеться в ній; з'ясуй незрозумілі слова і вирази; виділи в задачі умову і запитання; б) подумай, що означає кожне число; який зв'язок між числами; в) ця задача проста чи складена? Якщо складена, то спробуй розробити план розв'язування; г) якщо план не вдалося відразу скласти, то пригадай, яку подібну задачу розв'язували раніше; розв'яжи частину задачі; чи не можна тепер знайти відповідь на основне запитання? 264 Розділ XI. Навчання учнів розв'язувати текстові задачі У формуванні вмінь розв'язувати задачі велике значення мають і деякі спеціальні заходи навчального та виховного характеру. Дітей необхідно орієнтувати на таку настанову: над розв'язуванням задачі треба думати, оскільки прийоми знаходження відповіді невідомі, їх потрібно знайти. Тому при опрацюванні умови учнів не слід "підганяти", вони мусять мати час на обмірковування. Кожна нова задача не має виникати з "нічого", вона мусить спиратися на набуті вже знання і на повсякденний досвід, відповідати природній допитливості дитини. Водночас якщо задача розв'язана (засвоєна), то її слід використати для розв'язування інших задач, для відшукання простіших способів розв'язування та постановки нових перспектив. Загалом можна сказати, що процес формування вмінь розв'язувати задачі неперервний. Учні розв'язують задачі на кожному уроці математики і в процесі виконання домашніх завдань. Формування вмінь передбачає також ознайомлення з новим видом задач, перехід від одного виду задач до іншого та зв'язок між ними, повторне розв'язування задач, різновиди творчої роботи над задачами. Розгляньмо деякі види творчої роботи. Повторне розв'язування задач. Якщо задачу повторно розв'язують відразу після запису останньої дії і відповіді, то це буде момент первинного закріплення. Тут ми маємо на увазі повторне розв'язування через деякий час, тобто через кілька днів або тижнів. Цей прийом не належить безпосередньо до творчої роботи, але він відіграє певну роль при формуванні і закріпленні вмінь розв'язувати задачі. Маючи справу із задачею вдруге, учень краще усвідомлює зв'язки між величинами, алгоритм її розв'язування. Якщо при цьому він розв'яже задачу самостійно, то вона стане вже його "власною". Повторне розв'язування задач варто практикувати під час опитування та під час усних обчислень. Для цього добирають задачі на одну-дві дії. Один раз на місяць доцільно пропонувати учням для домашньої роботи повторно розв'язати кілька задач: одну — письмово, а решту — усно. Зміна елементів задачі. Зміна числових даних. Пропонують розв'язати задачу, аналогічну до розв'язаних на цьому чи попередніх уроках, але з іншими числовими даними. Здебільшого змінюють одне з даних. Задача. Упертій бригаді 7 сівалок, а в другій — на 2 сівалки менше. Скільки сівалок в обох бригадах? Завдання: а) розв'язати таку саму задачу, але щоб в ній було сказано, що в другій бригаді на 4 сівалки більше; б) розв'язати задачу, але число 7 замінити іншим числом; в) розв'язати задачу, але числові дані замінити так, щоб шукане число збільшилось. Виконуючи завдання, учні впевнюються, що задача розв'язується такими самими діями, якими й попередня. Відбувається процес узагальнення способу розв'язування. Це і є головна мета прийому зміни числових даних. У деяких випадках можна запропонувати дітям змінити числові дані так, щоб задачу можна було розв'язати іншим способом. Методика викладання математики в початкових класах 265 Зміна запитання. Застосування цього прийому наголошує на спрямовуючій ролі запитання для вибору необхідних зв'язків, стимулює учнів до всебічного аналізу задачної ситуації. Зміну запитання використовують також для постановки нових задач, "розширення" задачі. Задача. У першій каністрі 18 л бензину, а в другій —6 л. Скільки літрів бензину в двох каністрах? Завдання. Розв'язати інші задачі з такою самою умовою, але іншими запитаннями: а) на скільки літрів бензину в першій каністрі більше, ніж у другій? б) у скільки разів менше бензину в другій каністрі, ніж у першій? в) скільки літрів бензину потрібно долити, щоб в каністрах бензину стало порівну? Зміна сюжету задачі. Пропонують розв'язати таку саму задачу, але з іншими величинами. При цьому учні вчаться з'ясовувати умови застосування в реальній дійсності тих чи інших залежностей. Зміна, деяких зв'язків. Такий прийом привертає увагу дітей до значення окремих слів і виразів у контексті задачі. Вони поступово усвідомлюють, що незначні на перший погляд зміни ведуть до істотних змін у ході розв'язування, роблять висновок про можливість зміни характеру залежностей між величинами. Задача. У білки 12 горіхів, а в хом 'яка — на 3 горіхи менше. Скільки горіхів у білки і хом 'яка разом ? Завдання. Замінити в умові вираз "на 3 горіхи менше" іншим — "у 3 рази менше" ("на 3 горіхи більше", "у 3 рази більше") і розв'язати задачу. Варто практикувати також поступове ускладнення умови задачі. Спочатку учням пропонують кілька змінених задач, в яких збільшується кількість числових даних, включаються додаткові зв'язки. Запитання задачі залишається без змін. Цей прийом дає змогу бачити, як ускладнення числових даних і зв'язків впливає на хід розв'язування задач. Задача. Турист за день пройшов 10 км і проїхав на автобусі 180 км. Скільки кілометрів пройшов і проїхав турист за день? Змінені задачі: /. Турист ішов 2год по 5 км/год та їхав на автобусі 180 км. Скільки кілометрів пройшов і проїхав турист разом ? 2. Турист ішов 2 год по 5 км/год та їхав 3 год автобусом зі швидкістю 60 км/год. Скільки кілометрів пройшов і проїхав турист разом? 3. Пішки турист ішов 2 год, а автобусом їхав на 1 год більше. Він ішов зі швидкістю 5 км/год, а їхав в автобусі зі швидкістю 60 км/год. Скільки кілометрів пройшов і проїхав турист разом ? Розв'язування задач різними способами. Деякі арифметичні задачі допускають два чи кілька способів розв'язування. Такі задачі є ефективним навчальним матеріалом, на основі якого в учнів пробуджується допитливість, самостійність мислення. Намагання знайти інший шлях розв'язування тієї самої задачі сприяє підвищенню емоційного стану школярів. Розв'язування задач різними способами веде до розвитку вміння всебічно аналізувати задачну ситуацію. Проте тут важливий ще і сам факт існування266 РозділXI. Навчання учнів розв 'язувати текстові задачі різних способів розв'язування. Усвідомлення цього є кроком до пошуку кращого способу, що водночас призводить до встановлення нових зв'язків між величинами або використання відомих зв'язків у нових умовах. Задача. У хлопчика було 8 білих і 7 чорних кролів. 5 чорних кролів він передав шкільній кролефермі. Скільки кролів стало у хлопчика? Розв'яжіть задачу двома способами. Перший спосіб Другий спосіб 1) Скільки всього кролів як 1) Скільки чорних кролів у хлопчика? сії і. залишилося? 2) Скільки кролів стало чц,. 2) Скільки кролів стало у хлопчика? у хлопчика? Зауважимо, що розв'язання, відмінні між собою лише порядком виконання дій, не є різними. Складання виразів за умовою задачі. Як творчий вид роботи над задачею можна розглянути завдання, основна мета яких полягає не у знаходженні числового результату, а у складанні числових виразів. Роль завдань, що сприяють розвитку вмінь учнів записувати деяку конкретну життєву ситуацію математичною мовою, надзвичайно велика. Особливо корисні вони як засіб підготовки дітей до розв'язування задач складанням рівняння. Наведемо зразки таких завдань (див. також розділ XIII): 1. У шкільному хорі 42 учні, а в гуртку малювання — 14. Використовуючи ці числа і знак дії, записати, скільки учнів у хорі і в гуртку малювання разом. Відповідь. 42 + 14. Змінюючи вимогу до тієї самої умови, можна показати її роль у виборі дії. Так, до розглянутої умови доцільно додати ще такі вимоги: записати у вигляді виразу, на скільки більше учнів у шкільному хорі, ніж у гуртку малювання (42 - 14); записати у вигляді виразу, в скільки разів у гуртку малювання менше учнів, ніж у шкільному хорі (42 : 14). 2. На дереві сиділо 28 галок. 14 галок полетіло, а 7 — прилетіло. Записати у вигляді виразу, скільки галок стало на дереві. Відповідь. 28 — 14 + 7. 3. Лінійка коштує 45 коп., косинець — 40 коп. і блокнот — 90 коп. (Цю умову подати у вигляді таблиці). Завдання: а) поясніть, що означають вирази: 45 + 40; 45-40; 45 + 40 + 90; 90:45; 90-45; 90 - (45 + 40). Відповідь. 45 + 40 — вартість лінійки і косинця; 45 - 40 — на стільки копійок лінійка дорожча, ніж косинець; 45 + 40 + 90 — вартість лінійки, косинця і блокнота; 90 : 45 — у стільки разів лінійка дешевша, ніж блокнот і т. ін.; б) складіть вирази, за допомогою яких можна визначити, скільки треба заплатити за лінійку і блокнот (45 + 90); на скільки копійок косинець дешевший, ніж блокнот (90 - 40); у скільки разів більше треба заплатити за блокнот, ніж за лінійку (90 : 45); в) запишіть у вигляді виразів, яку здачу одержить учень з двох гривень, якщо купить лінійку (200 — 45); лінійку і блокнот (200 - (45 + 90)). > 4. Купили 4 м тканини по 8 грн. за метр. Усього заплатили 32 грн. Методика викладання математики в початкових класах 267 Використовуючи умову, поясніть, які величини можна знайти за допомогою виразів: 8 • 4; 32 : 4; 32 : 8. Відповідь. 8 • 4 — вартість всієї тканини; 32 : 4 — ціна 1 м тканини; 32 : 8 — кількість куплених метрів тканини. 5. Мотоцикліст їхав 3 год зі швидкістю 60 км/год і проїхав 180 км. Складіть вирази для знаходження швидкості, часу і відстані. Відповідь. 180 : 3 — швидкість; 180 : 60 — час; 60 • 3 — відстань. 6. Турист ішов пішки 3 год зі швидкістю 4 км/год та їхав велосипедом 2 год зі швидкістю 16 км/год. Поясніть, які з поданих виразів мають зміст, а які — ні: 4 • 3; 16 • 2; 16 - 4; 16 + 4; 16 : 2; 2 • 3; 3 + 2; 4 - 3; 4 • 3 + 16 - 2; 16 • 2 - 4 • 3. Складання задач. Завдання на складання задач ефективні насамперед для розвитку уявлень учнів про структуру задач та узагальнення способу їх розв'язування. Цей вид роботи корисний і для досягнення багатьох інших цілей, зокрема для того, щоб виявити, як діти усвідомлюють способи розв'язування задач певного виду. Якщо учень самостійно складає задачу з певними залежностями між величинами, то він добре розуміє ці залежності і легко сприйматиме відповідний зв'язок у заданій задачі. У спеціальних дослідженнях з методики математики і досвіду роботи самих учителів обґрунтовано доцільність застосування багатьох прийомів складання задач, кожен з яких має свою функцію. Подамо їх перелік: • складання задач на зазначену дію; • складання задач за виразом чи розв'язком; • складання задач на задану зміну величин чи залежність між величинами. Наприклад, скласти задачу про збільшення маси кроля; скласти задачу на зменшення числа в кілька разів; скласти задачу на знаходження ціни (вартості чи кількості товару; відстані, швидкості чи часу; норми витрат продуктів, урожайності тощо); • складання задач певного виду. Наприклад, скласти задачу на знаходження невідомого зменшуваного; на знаходження третього доданка за відомою сумою і двома доданками; на різницю двох добутків; на зустрічний рух, в якій потрібно було би знайти час руху; • складання обернених задач. Заслуговує на увагу складання і розв'язування задач за числовими даними, що подаються в поєднанні з відповідними малюнками (мал. 135). 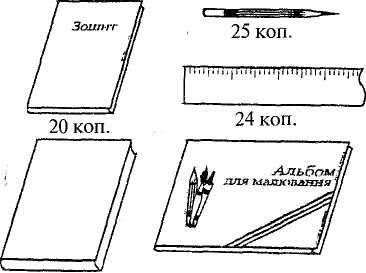 60 коп. Мал. 135 40 коп. 268 РозділХІ. Навчання учнів розв'язувати т< Запитання: 1. На скільки копійок олівець дешевший від альбому для малювання? 2. Скільки копійок коштують 2 зошити і книжка разом? 3. У скільки разів книжка та альбом дорожчі за зошит? 4. Скільки копійок заплатять за 3 олівці і 2 лінійки разом? Як вид творчої роботи практикується також порівняння задач з тією чи іншою метою: звернути увагу учнів на те, що ті самі слова можуть бути як визначальними для вибору дій, так і не визначальними; визначити, яка з двох задач проста, а яка — складена; з'ясувати, яка з даних задач належить до зазначеного виду. Навчання дітей розв'язувати задачі — це не ізольований процес, він безпосередньо пов'язаний із загальною атмосферою в класному колективі. Слід виховувати інтерес до самостійного розв'язування задач, заохочувати учнів знаходити раціональні прийоми обчислення. РОЗДІЛ XII ФОРМУВАННЯ ПОЧАТКОВИХ УЯВЛЕНЬ ПРО ДРОБИ У молодших школярів необхідно створити конкретні уявлення про процес утворення частин від цілого предмета чи сукупності предметів. З цією метою вже в 3 класі дітей ознайомлюють з частинами, їх записом, вчать знаходити частину числа та число за відомою його частиною. У 4 класі продовжують працювати над засвоєнням частини числа, учнів ознайомлюють з дробами та їх записом, вчать порівнювати частини, знаходити кілька частин від числа, дріб від числа, розв'язувати складені задачі, що передбачають знаходження дробу від числа. Розглядають ці питання з допомогою наочності, виконуючи практичні вправи, пов'язані з кресленням, вимірюванням, перегинанням, практичним поділом круга, прямокутника, смужки на рівні частини. §43. Ознайомлення з частинами Діти часто чують від старших слова "півкілограма яблук", "третя частина, кавуна", "чверть години" тощо. Цей життєвий досвід учнів треба впорядкувати і систематизувати. Правильні уявлення про частини, а пізніше про дроби будуть сформовані тоді, коли діти своїми руками зроблять, наприклад, половину круга, знайдуть четверту частину смужки та ін. Покажемо, як ознайомлювати учнів з частинами. Учитель запитує, хто бачив половину хлібини (кавуна, яблука тощо), ставить завдання показати половину кружечка, розділити навпіл смужку паперу. Перегинаючи круг, смужку паперу навпіл, діти роблять висновок, що половини одного й того самого круга чи тієї самої смужки паперу рівні між собою. На цьому самому уроці вони розглядають малюнок (мал. 136). 12 см 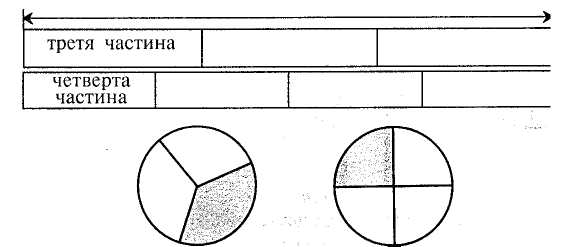 Мал. 136270 Розділ XII. Формування початкових уявлень про дроби Перша смужка поділена на З рівні частини, а друга — на 4. Знайдіть, чому дорівнює третя і четверта частини смужки. Третя частина ще називається третина, а четверта — чверть. Покажіть на малюнках третю і четверту частини круга. Учні знаходять половину числа 12, третину числа 15, чверть числа 8 та ін. Діти повинні усвідомити, що для знаходження половини числа його треба поділити на 2, для знаходження третини — поділити на 3, для знаходження чверті — поділити на 4. Наприкінці навчання у 2 класі і впродовж 3 класу учні знаходять довжини вказаних частин смужки, частини чисел (без позначення частин числа цифрами). Приклади: 1. Знайдіть половину, третину і чверть числа 12. 2. Виміряйте довжину кожної смужки, а потім знайдіть довжину четвертої частини першої смужки і шостої частини другої. Результати обчислення перевірте вимірюваннями (мал. 137). четверта частина 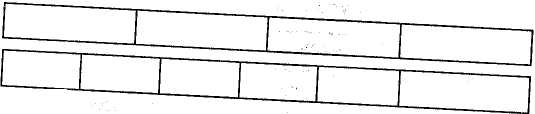 шоста частина Мал. 137 3. Знайдіть п'яту частину 1 дм, четверту частину 2 дм, половину 1 м. 4. Скільки хвилин становить одна шоста години? Одна четверта? Одна .кетя? Половина години? У 3 класі дітей вчать позначати частини цифрами. їм потрібно спочатку показати поділ першого круга на дві рівні частини, другого — на чотири рівні частини. Тоді необхідно з'ясувати з ними, на скільки рівних частин поділені дані круги. Після цього слід розглянути малюнки в підручнику (мал. 138). 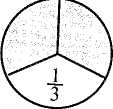 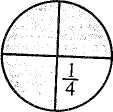 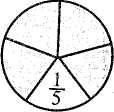 Методика викладання математики і початкових класах 271 показує, що взяли одну таку частину. Терміни "чисельник", "знаменник" не вводять. Просто кажуть, що число під рискою показує, на скільки рівних частин поділили круг (смужку), а число над рискою показує, що взяли одну таку частину. Під час виконання вправ на знаходження частини смужки (круга, квадрата тощо) доцільно звертати увагу учнів, що в цілій смужці (крузі, квадраті) є дві половини, три третіх частини, чотири четвертих частини і т. ін. Задачі на обчислення частин числа діти розв'язують, спираючись на розуміння процесу знаходження частини числа. Щоб знайти, наприклад, четверту частину числа, треба це число поділити на чотири; щоб обчислити довжину 1/3 смужки, потрібно довжину смужки поділити на 3. Задача. У шкільному саду росте 60 дерев. 1/3 дерев становлять яблуні і 1/4 — груші. Скільки яблунь і груш у саду разом? Яку частину дерев у саду становлять яблуні? (Одну третю частину). Як знайти третю частину від числа 60? (Треба 60 поділити на 3). Скільки яблунь в саду? (60 : 3 = 20 (ябл.)). (Щодо груш аналогічні міркування). В основі розв'язування задач на знаходження числа за його відомою частиною лежить розуміння учнями того, що дві других (дві половини), три третіх, чотири четвертих і т. ін. становлять ціле, весь предмет. Задача. Відрізок АК становить 1/4 відрізка АВ і дорівнює 20 мм. Знайдіть довжину відрізка АВ (мал. 139). Мал. 139 Яку частину відрізка АВ становить відрізок АК? (Одну четверту частину). Скільки таких четвертих частин є у цілому відрізку АВ? (У відрізку АВ вміщується таких чотири четвертих частини). Яка довжина однієї четвертої частини відрізка АВ?(2§ мм). Як знайти всю довжину відрізка АВ? (Треба по 20 мм взяти 4 рази, тобто 20 • 4 = 80 (мм)). Не варто формулювати спеціальні правила для розв'язування задач, пов'язаних зі знаходженням частини числа та числа за відомою його частиною, важливо лише, щоб учні розуміли суть процесу. < Мал. 138 Учитель пояснює, що частини записують за допомогою двох цифр. Наприклад, третю частину круга, смужки позначають так: 1/3. Число 3 показує, що круг, смужку або іншу фігуру поділили на три рівні частини, а число 1 272 Розділ XII. Формування початкових уявлень про дроби §44. Ознайомлення з дробами У 4 класі актуалізують знання школярів про частини: їх утворення, позначення, знаходження частини числа та числа за його відомою частиною, вчать порівнювати частини. Порівнюють частини тільки з опорою на унаочнення (мал. 140). Мал. 140 Користуючись малюнком, учні з'ясовують, наприклад, скільки четвертих частин у половині, скільки восьмих частин у цілому і т. ін. Наочно бачать, що 1/4 < 1/2; 1/2 > 1/8; 1/8 > 1/10 і т. ін. Учні мають зрозуміти, що коли ціле поділити на рівні частини, то кожна частина буде менша від цього цілого; чим на більшу кількість частин поділено ціле, тим меншою буде кожна його частина. Із дробами учні ознайомлюються, виконуючи під керівництвом учителя такі вправи: 1. На скільки рівних частин поділено кожний квадрат (мал. 141)? Мал. 141 Як називається незаштрихована частина у квадраті? Скільки таких частин у квадраті заштриховано? 2. Полічіть, на скільки рівних частин поділено кожний круг (мал. 142). Скільки таких частин заштриховано? Мал. 142 Методика викладання математики в початкових класах 273 Ми вже вміємо позначати цифрами одну частину числа. Яка частина першого круга заштрихована? (1/6). (Учитель записує це число на дошці). Скільки таких шостих частин заштриховано у другому крузі? (2). Тобто заштриховано 2/6 частини. (Вчитель записує на дошці). Скільки таких шостих частин заштриховано у третьому крузі? І т. д. Числа виду 1/2, 2/3, 3/4, 1/6, 2/3, 5/6 називаються дробовими числами. Число 5/6 — дріб, 5 — чисельник дробу, а 6 — знаменник дробу. Число під рискою дробу — знаменник дробу — показує, на скільки рівних частин поділено ціле. Число над рискою дробу — чисельник дробу — показує, скільки взято рівних частин цілого. Для закріплення матеріалу учні виконують такі вправи: а) запишіть у вигляді дробу, яку частину прямокутника заштриховано (мал. 143); Мал. 143 б) прочитайте дроби і поясніть, як їх утворено (мал. 144).
І Мал. 144 Здобуті знання про дроби та їх зображення використовують під час розв'язування задач на знаходження дробу від числа. Пояснення знаходження дробу від числа подають на основі готового розв'язання. Задача. Довжина відрізка АВ дорівнює 10 см. Чому дорівнює 3/5 цього відрізка ? (Мал. 145). 10 см ________VI  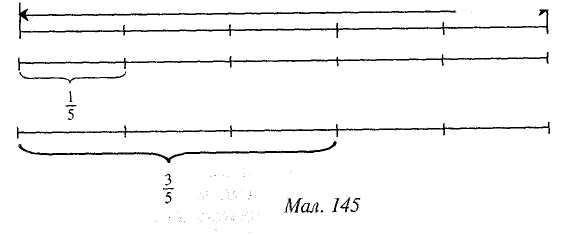 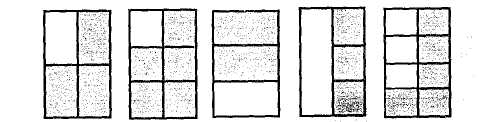 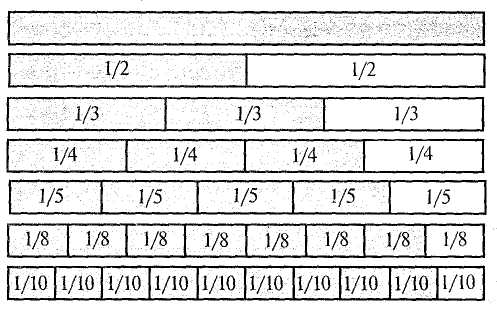 272 Розділ XII. Формування початкових уявлень про дроби §44. Ознайомлення з дробами У 4 класі актуалізують знання школярів про частини: їх утворення, позначення, знаходження частини числа та числа за його відомою частиною, вчать порівнювати частини. Порівнюють частини тільки з опорою на унаочнення (мал. 140). Мал. 140 Користуючись малюнком, учні з'ясовують, наприклад, скільки четвертих частин у половині, скільки восьмих частин у цілому і т. ін. Наочно бачать, що 1/4 < 1/2; 1/2 > 1/8; 1/8 > 1/10 і т. ін. Учні мають зрозуміти, що коли ціле поділити на рівні частини, то кожна частина буде менша від цього цілого; чим на більшу кількість частин поділено ціле, тим меншою буде кожна його частина. Із дробами учні ознайомлюються, виконуючи під керівництвом учителя такі вправи: 1. На скільки рівних частин поділено кожний квадрат (мал. 141)? Мал. 141 Як називається незаштрихована частина у квадраті? Скільки таких частин у квадраті заштриховано? 2. Полічіть, на скільки рівних частин поділено кожний круг (мал. 142). Скільки таких частин заштриховано? Мал. 142 Методика викладання математики в початкових класах 273 Ми вже вміємо позначати цифрами одну частину числа. Яка частина першого круга заштрихована? (1/6). (Учитель записує це число на дошці). Скільки таких шостих частин заштриховано у другому крузі? (2). Тобто заштриховано 2/6 частини. (Вчитель записує на дошці). Скільки таких шостих частин заштриховано у третьому крузі? І т. д. Числа виду 1/2, 2/3, 3/4, 1/6, 2/3, 5/6 називаються дробовими числами. Число 5/6 — дріб, 5 — чисельник дробу, а 6 — знаменник дробу. Число під рискою дробу — знаменник дробу — показує, на скільки рівних частин поділено ціле. Число над рискою дробу — чисельник дробу — показує, скільки взято рівних частин цілого. Для закріплення матеріалу учні виконують такі вправи: а) запишіть у вигляді дробу, яку частину прямокутника заштриховано (мал. 143); Мал. 143 б) прочитайте дроби і поясніть, як їх утворено (мал. 144).
І Мал. 144 Здобуті знання про дроби та їх зображення використовують під час розв'язування задач на знаходження дробу від числа. Пояснення знаходження дробу від числа подають на основі готового розв'язання. Задача. Довжина відрізка АВ дорівнює 10 см. Чому дорівнює 3/5 цього відрізка ? (Мал. 145). 10 см ________VI     274 Розділ XII. Формування початкових уявлень про дроби Розв'язання 1) Скільки сантиметрів в 1/5 відрізка АВ? 10:5 = 2 (см). 2) Чому дорівнює 3/5 відрізка АВ? 2-3 = 6 (см). Відповідь. Довжина 3/5 відрізка АВ дорівнює б см. Пррпонують учням і абстрактні задачі на знаходження дробу-віц числа. Задача. Знайдіть 5/9 від 64 260.■.-::■ удоці 64 260:9 • 5 = 35 700. У 4 класі діти розв'язують складені задачі, що передбачають знаходження дробу, а саме: 1. Задачі, в яких треба знайти кілька частин відданого числа (знайти дріб від числа). Задача. Маса гарбуза дорівнює 14 кг. Від гарбуза відрізали 2/7 його маси і зварили кашу. Скільки кілограмів гарбуза було витрачено на кашу? 2. Задачі, в яких треба знайти кілька частин від решти. Задача. Площа дослідного поля становить 86 000 м2. Частину цього поля у вигляді прямокутної ділянки зі сторонами 320 м і 100 м засіяно гречкою. 3/4решти поля засіяно просом. Скільки квадратних метрів становить площа поля, засіяна просом? 3. Задачі, в яких треба знайти кілька частин від того числа, яке знайшли. Задача. Туристу треба було пройти 180 км. За перший день він пройшов 1/6 всього шляху, а за другий — 4/5 того шляху, який пройшов за перший день. Скільки кілометрів пройшов турист за два дні? Завдання на знаходження дробу від числа часто пропонують для усних обчислень. Вони корисні для закріплення учнями знань про співвідношення між мірами величин. Наприклад: 1. Скільки метрів у 3/4 км? У 2/5 км? У 3/10 км? 2. Скільки кілограмів у 3/4 ц? У 3/4 т? У 3/5 ц? 3. Знайдіть: 2/7 від 35; 3/4 від 40; 2/5 від 200. РОЗДІЛ XIII ПРОПЕДЕВТИКА АЛГЕБРИ В ПОЧАТКОВИХ КЛАСАХ Початковий курс математики містить елементи алгебри. Вивчення елементів алгебри в початкових класах сприяє узагальненню знань учнів про число, арифметичні дії і відношення. Школярі одержують початкові відомості про математичні вирази, числові рівності і нерівності, ознайомлюються з буквеною символікою, розв'язують задачі з буквеними даними, вчаться розв'язувати найпростіші рівняння і нерівності, набувають початкових умінь розв'язування задач на одну дію за допомогою рівнянь, у них формуються перші уявлення про функціональну залежність. |
