методика математики книга. Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
|
§2. Методика початкового навчання математики та інші науки - Методика початкового навчання математики належить до педагогічних наук: вона враховує закони і правила логіки, закономірності психології, положення дидактики, рекомендації загальної методики математики. Методика і логіка. Логіка визначає правила міркувань: як людина має мислити, щоб від правильних засновків дійти правильних висновків. Закони і правила логіки методика використовує в процесі аналізу та структурування навчального матеріалу, формулювання означень математичних понять, встановлення зв'язків між поняттями, відшукування шляхів розв'язування^ задач. Методика також визначає, які логічні знання й уміння потрібні учням для свідомого засвоєння математичних знань. Розвиток логічного мислення учнів є одним із завдань викладання математики в школі. Сам учитель повинен знати, що таке поняття, означення, доведення, класифікація; які існують види означень, методи доведення, правила класифікації. А все це — логічні категорії. Можна сказати, що без логіки немає і навчання. Однак вирішальним у навчанні є вплив психолого-педагогічних чинників. Без них логіка не навчає, тобто не проникає в свідомість учнів. Методика і психологія. Психологія навчання вивчає закономірності психіки дитини, а також вікові та індивідуальні особливості дітей, які проявляються в процесі засвоєння знань. Діяльність учителя на заняттях з учнями так чи інакше містить вплив на їхню психіку: на відчуття, сприймання, пам'ять, мислення, емоції, почуття і волю; на характер, здібності і на особистість загалом. Отже, вчитель має знати особливості розвитку психічних процесів молодших школярів і вміти створювати в учнів оптимальний психічний стан для конкретного виду навчальної діяльності. У навчанні насамперед треба активізувати мислення учнів. Саме психолог аналізує, як мислить учень. Вивчаючи мислительні операції, які здійснюють учні в процесі навчання, психологи розчленовують багато з тих понять і операцій, які методисти розглядають як цілісні. Це допомагає в розкритті процесу мислення учнів, вивченні його сильних і слабких сторін. У навчально-виховній роботі велике значення мають закономірності випереджального відображення. Учень повинен передбачати результати своїх вчинків і дій. Слід сказати, що методисти-математики не тільки використовують дані, здобуті психологією навчання, а й самостійно вивчають процес засвоєння математичних знань учнями та його результати. Методика і дидактика. Дидактика розробляє принципи навчання, форми організації навчальної роботи, методи навчання. Методика математики враховує дані дидактики, але в їх використанні відображає особливості своєї науки. Принципи навчання діють на всіх ступенях навчання з усіх предметів. Проте в межах навчального предмета деякі з них набувають специфічності. Це стосується, зокрема, принципу наочності, зв'язку теорії з практикою. Розділ І. Методика початкового навчання математики як педагогічна наука 12 Методика математики "вибирає" з дидактики потрібні методи, аналізує доцільність їх застосування і розробляє зразки застосування. Великої конкретності набуває урок в розробках методистів-математиків. У кожному з компонентів уроку математики відчутні загальні положення дидактики. Водночас дидактика збагачується педагогічними фактами, які виявляють вчителі чи методисти-дослідники в процесі навчання молодших школярів математики. Методика початкового навчання математики і загальна методика математики. Загальна методика математики розглядає такі питання: шляхи формування математичних понять; використання дедукції та індукції у викладанні математики, аналізу і синтезу в процесі розв'язування задач; методи навчання математики; особливості уроку математики; наочність у навчанні математики. Закономірності, встановлені загальною методикою математики, застосовуються методикою початкового навчання математики з урахуванням, по-перше, вікових особливостей молодших школярів, по-друге, специфіки програмного матеріалу, що опрацьовується в тому чи іншому класі. Зауважимо, що методика викладання математики в початкових класах має багато спільного з методикою рідної мови, трудового навчання, природознавства. Вчителю це важливо враховувати, щоб правильно ^здійснювати міжпредметні зв'язки. Методика і математика. Основою курсу математики початкових класів є лічба, нумерація і чотири арифметичні дії над цілими невід'ємними числами. Одна з особливостей арифметики полягає в тому, що багато з її положень хоч і важкі для доведення, але легко відкриваються спостереженням числових виразів. Вони відмінні від спостережень тих об'єктів, що безпосередньо впливають на органи чуття. Отже, виникає завдання розвивати в дітей спостережливість в галузі арифметики, а також уміння використовувати такі спостереження для індуктивних висновків. Зміст арифметики містить також багато матеріалів для дедуктивних міркувань. Це, зокрема, стосується застосування властивостей арифметичних дій для обґрунтування прийомів обчислень, врахування залежностей між. величинами під час розв'язування задач. На методику викладання впливає не тільки зміст математики як навчального предмета, а. й теоретичні положення математичної науки, що стосуються основ математики, її методології. Методика математики в своєму розвитку спирається, як і математика, на теорію пізнання. Для правильного вирішення методичних проблем потрібно певною мірою враховувати ті етапи, які пройшла в своєму історичному розвитку математика як наука. Основні математичні положення здобуті з дійсного світу за допомогою абстракції. У науці вони дістають самостійний логічний розвиток, а потім знову знаходять застосування в трудовій діяльності людей. Цей процес певною, мірою відображається і в методиці викладання математики. Учням треба показувати застосування математики в житті, в трудовій діяльності людини;, тренувати в застосуванні математичних знань для виконання обчислювальних, розрахункових, графічних і вимірювальних робіт. Цим підвищується Методика викладання математики в початкових класах 13 інтерес школярів до вивчення математики, закладаються основи правильного розуміння значення математики в житті людей. §3. Методи наукового дослідження, що застосовуються в процесі розробки методики викладання початкового курсу математики Проблемами удосконалення методики навчання займаються працівники й аспіранти відповідних науково-дослідних інститутів, викладачі педагогічних ВНЗ, а також вчителі-новатори. Загалом дослідження проходять ряд етапів. Перший етап передбачає виконання трьох завдань. Перше з них полягає в тому, щоб у процесі аналізу стану в теорії і практиці відшукати найбільш актуальну методичну проблему. Друге — зібрати попередній матеріал, щоб конкретизувати можливі причини виникнення проблеми. Третє — розробити гіпотезу, тобто припущення, про можливі шляхи вирішення цієї проблеми. З урахуванням гіпотези визначаються конкретні завдання дослідження і складається методика дослідження. Другий етап — це конкретизація і реалізація методики дослідження. Він здебільшого передбачає розробку певної навчальної системи (наприклад, системи вправ чи задач) і проведення формуючого експерименту, тобто навчання в кількох класах чи навіть в окремих районах за розробленою системою. Проведення формуючого експерименту передбачає застосування різних методів, зокрема і таких, що дають змогу здобути числові показники результатів навчання. Третій етап — статистична обробка й інтерпретація даних дослідження. Кількісні показники підтверджують або відхиляють робочу гіпотезу. Четвертий етап — висновки і пропозиції, що грунтуються на матеріалах дослідження. В методичних дослідженнях висновки, як правило, доповнюються конкретними методичними рекомендаціями щодо їх реалізації у масовій школі. В дослідженнях з проблем методики початкової математики використовують як загальнонаукові, так і конкретно-наукові методи (тобто методи, характерні для педагогічних досліджень). Загальнонаукові методи поділяються на емпірико-теоретичні, теоретичні й емпіричні. Розглянемо основні методи кожної групи. Емпірико-теоретичні загальнонаукові методи Аналіз і синтез. Ці два методи взаємопов'язані і доповнюють один одного як дві нерозривні сторони діалектично єдиного процесу пізнання. Сутність аналізу полягає у зведенні складних понять до більш загальних і простих. Типовим зразком аналізу є класифікація. За допомогою синтезу отримують нове знання про об'єкт на основі з'ясування відношень, властивостей, взаємодії і зв'язків між його частинами. Індукція і дедукція. Сутність індукції полягає в тому, що зі знання про частину предметів якої-небудь їх сукупності роблять висновок про всю сукупність. Індуктивний умовисновок завжди має вірогідний характер. Розділ І. Методика початкового навчання математики як педагогічна наука 14 Застосування методу дедукції полягає у використанні загальних наукових положень для дослідження конкретних явищ. Моделювання. Існують три основні форми створення моделі: матеріальна, знакова та концептуальна (мислительна). Сутність моделювання полягає в заміні об'єкта моделлю, що містить потрібні з точки зору мети дослідження риси, властивості, відношення чи зв'язки об'єкта. Модель дає змогу значно розширювати можливості експерименту. Результати експерименту на моделі поширюють на оригінал. Теоретичні загальнонаукові методи Узагальнення. Сутність узагальнення як загальнонаукового методу полягає в переході від одиничного до загального (виявленням загальних ознак) і поширенні здобутого знання на часткове, одиничне. Метод узагальнення є засобом розробки нових наукових понять, законів і теорій. Абстрагування. Метод абстрагування заснований на формуванні ідеального образу реального об'єкта в результаті мисленого виділення ряду ознак, властивостей, зв'язків чи відношень, що цікавлять дослідника. Інші властивості і сторони об'єкта при цьому не враховуються. Сутність абстрагування полягає в тому, що додають до частини відомих об'єкту ознак нову інформацію, що з них випливає. Абстрагування в процесі наукового пізнання тісно пов'язане з в конкретизацією. Конкретне розуміють як таку категорію, що виявляє єдність, цілісність об'єкта в усій багатогранності його зв'язків і відношень. Згідно із загальним законом розвитку людського пізнання перехід від абстрактного до конкретного є одним з принципів дидактичної логіки. Емпіричні загальнонаукові методи До емпіричних загальнонаукових методів належать: спостереження, порівняння й експеримент. Спостереження. Сутність спостереження як методу пізнання полягає в систематичному і цілеспрямованому сприйманні об'єкта, що передбачає: постановку мети, розробку певної системи спостережень, описування його результатів, формування висновків. Результати спостережень оформлюють у вигляді таблиць, схем, діаграм, графіків, протоколів, фотодокументів. Учителі використовують спостереження для вивчення праці учнів на уроках, процесу засвоєння ними математичних знань. Спостереження процесу навчання математики проводяться переважно на уроках. Спостерігається урок загалом чи окремі його частини, наприклад, спостереження за самостійною роботою учнів у процесі розв'язування задач. Порівняння як метод дослідження застосовується для виявлення кількісної і якісної характеристик об'єктів, класифікації, впорядкування, оцінювання тих чи інших явищ. Як пізнавальна операція порівняння служить за основу для міркування про схожість чи відмінність об'єктів. Експеримент. У методологічному аспекті експеримент — це перехід дослідника від пасивного до активного способу діяльності. Експеримент дає змогу спостерігати за ходом явища, що вивчається, активно впливати на Методика викладання математики в початкових класах 15 його зміни; відтворювати це явище в адекватних умовах. Експеримент служить за основу для перевірки гіпотези чи передбачення теорії. До конкретно-наукових методів належать: метод педагогічних спостережень, метод вивчення документальних джерел, метод опитування і контрольних робіт, експертний метод, метод педагогічного експерименту. Метод педагогічних спостережень є активною формою наукового пізнання об'єктів (предметів, явищ) з метою одержання початкових або уточнення існуючих уявлень про них на основі накопичення фактів. Він ефективний за умов конкретності постановки мети, визначення об'єкта й предмета дослідження, чіткості плану дослідження, мінімальності досліджуваних ознак і однозначності критеріїв їх оцінювання, типовості та природних умов спостережень, можливості відтворення спостережень, обгрунтованості частоти і тривалості спостережень, можливості передбачення, попередження й уникнення помилок. Як правило, спостереження здійснюються в поєднанні з іншими методами. Метод вивчення документальних джерел. До педагогічних документів належать: класні журнали, щоденники учнів, робочі плани вчителів, звіти класних керівників, керівників гуртків, протоколи педагогічних рад, навчальні плани, програми, протоколи зборів, зошити учнів, контрольні роботи, саморобні наочні посібники. Аналіз письмових робіт учнів дає змогу зробити висновки як про процес їх виконання, так і про результати. Істотне значення має аналіз помилок учнів. На його основі виявляють типові ускладнення й індивідуальні особливості в засвоєнні математичних знань учнів. Метод опитування та контрольних робіт. Метод опитування спирається на цілеспрямоване одержання інформації способом усного опитування (бесіда, інтерв'ю, анкетування) за наперед складеною програмою, що містить прямі і непрямі запитання. Метод усного опитування часто поєднується з проведенням контрольних робіт, виконанням практичних завдань. Бажано забезпечити планомірний характер запитань, їх лаконічність, конкретність, однозначність, послідовність, постановку запитань від простих до складних; оперативність і зручність фіксації відповіді; можливість одержання кількісної інформації. Експертний метод. Експертні методи педагогічних досліджень спираються на думку спеціалістів, які дають апріорні кількісні або рангові оцінки явищ, що вивчаються. Метод педагогічного експерименту. За своєю сутністю метод педагогічного експерименту є методом комплексного характеру, бо він передбачає спільне використання методів спостережень, бесід, інтерв'ю, анкетування, створення спеціальних ситуацій та ін. Залежно від мети і змісту експерименту визначається його тривалість: протягом кількох уроків, під час вивчення певної теми, протягом навчальної чверті або всього навчального року. Дослідник розробляє плани чи конспекти уроків з включенням до них засобів або методичних прийомів, які будуть перевірятися. За цими планами вчитель чи сам дослідник проводить уроки. Розділ І. Методика початкового навчання математики як педагогічна наука 16 Хід уроку фіксується в протоколах, ведуться спостереження за процесом засвоєння знань учнів, проводяться спеціальні роботи (усні й письмові) щодо обліку знань учнів. Для порівняння визначають контрольні класи. За рівнем знань учні цих класів однакові з учнями експериментальних класів. У контрольних та експериментальних класах викладання проводиться однаково, за винятком використання тих посібників чи методів, що застосовуються в експериментальних класах. Облік знань, проведений в експериментальних класах і контрольних класах, покаже вплив досліджуваного чинника на якість знань учнів. Підсумовуючи сказане про шляхи дослідження проблем методики викладання математики, зазначимо, що історично вони були узагальненням передового досвіду вчителів. Це джерело не відкидається й нині, але застосовують і нові методики навчання математики, що є результатом наукових досліджень. При цьому враховуються нові напрямки в самій науці математики, дані психолого-педагогічних досліджень, рекомендації науково-методичних семінарів, конференцій. Результати наукових досліджень спочатку перевіряються на практиці роботи окремих учителів і шкіл, а потім ефективні методи запроваджуються в масову практику. РОЗДІЛ II ПОЧАТКОВИЙ КУРС МАТЕМАТИКИ ЯК НАВЧАЛЬНИЙ ПРЕДМЕТ У системі навчальних предметів початкової школи завдання і зміст вивчення математики є порівняно найбільш стабільними, проте і вони з часом зазнають деяких змін. Тому питання освітніх, виховних і розвивальних завдань навчання математики в початкових класах розкриємо з урахуванням сучасної концепції початкового курсу математики. Загалом висвітлення питань розділу спирається на програму і підручники початкової школи, програму дитячого садка, програму і посібники з методики математики для 5—6 класів. ! §4. Освітні, виховні й розвивальні завдання навчання математики в початкових класах Більшість питань математичної освіти має бути засвоєна в початкових класах на такому рівні, щоб стати надбанням учнів на все життя. Решта питань програми з математики для початкових класів опрацювується з метою підготовки до ґрунтовного вивчення відповідного матеріалу в наступних класах. Математика в початкових класах має як практичне, так і духовне значення. Насамперед курс математики початкових класів забезпечує подальше вивчення математики в середніх класах. Математичні знання, набуті в початкових класах, потрібні в повсякденному житті, під час вивчення інших дисциплін, для розуміння повідомлень засобів масової інформації. Молодші школярі отримують початкові уявлення про ті принципи і закони, що є основою для математичних чинників, які вивчаються. Це насамперед стосується десяткової системи числення та властивостей арифметичних дій. Істотним на початковому етапі є оволодіння обчислювальними вміннями і навичками. Духовне призначення вивчення математики проявляється у формуванні національних і загальнолюдських цінностей, у внеску в розумовий розвиток, у становлення і розвиток моральних рис, в естетичне виховання людини. Розгляд математичних понять, розв'язування задач включає в процес пізнання різні прийоми і методи людського мислення. Важливим завданням математики в початкових класах є розвиток пізнавальних здібностей у дітей. Необхідно розвинути у них уміння спостерігати й порівнювати, виділяти риси схожості та відмінності у Розділ II. Початковий курс математики як навчальний предмет 18 порівнюваних об'єктах, виконувати такі мислительні операції, як аналіз, синтез, узагальнення, абстрагування, конкретизація. 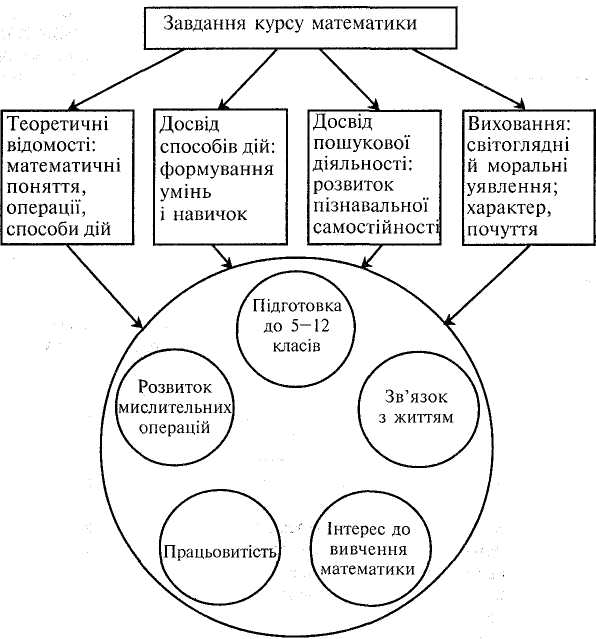 Провідна роль математики полягає у розвитку логічного мислення, формуванні алгоритмічного мислення, вихованні навичок розумової праці (планування, пошук раціональних шляхів, критичність). Формування в дітей уміння логічно мислити нерозривно пов'язане з розвитком у них правильної, точної, лаконічної математичної мови. Заняття математикою мають бути школою виховання характеру і почуттів. Навчання математики має формувати такі риси особистості, як працьовитість, охайність; сприяти розвитку волі, уваги, уяви учнів; стимулювати розвиток інтересу до математики; виробляти вміння вчитися і навички самостійної роботи. Вивчення математики має сприяти реалізації завдань виховання патріотизму, гуманності, чесності. Характерною рисою вихованості має стати готовність школяра долати труднощі, боротися зі злом. Методика викладання математики в початкових класах 19 |
