методика математики книга. Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
|
§10. Інструменти, прилади й моделі, технічні засоби навчання Вивчення чисел і величин ґрунтується на практичній діяльності учнів, пов'язаній з оволодінням уміннями і навичками вимірювання довжини відрізка, площі фігури, маси тіла, місткості посудини, часу. Вимірювати ці величини можна за допомогою інструментів. Вони поділяються на демонстраційні та індивідуальні. Деколи замість самих інструментів використовують їх моделі (моделі циферблата годинника, терезів, малки тощо). Класна рахівниця (мал. 8) служить необхідним наочним посібником для вивчення нумерації чисел в межах 1 000 000. Нею користуються з І класу, поступово збільшуючи кількість дротинок. На рахівниці під час вивчення чисел у межах 10 можна ознайомити учнів з тим, як отримати наступне і попереднє числа, як порівнювати числа (кількість кісточок на двох дротинках); демонструвати склад числа; проводити лічбу, додавати і віднімати числа; розкривати поняття "збільшити (зменшити) на кілька одиниць"; складати таблиці додавання і віднімання. Мал. 8 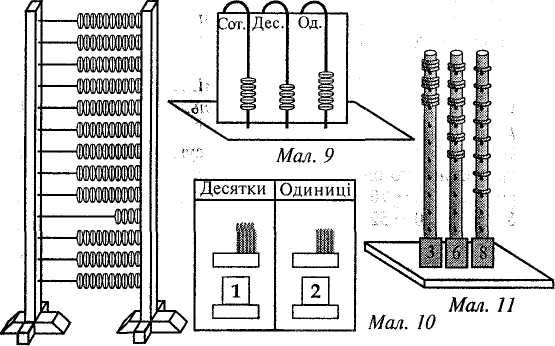 Методика викладання математики в початкових класах 39 Для ознайомлення з письмовою нумерацією чисел можна використати рахівниці з вертикальними дротинками (мал. 9), предметний абак (мал. 10). Для вивчення нумерації чисел та окремих випадків додавання і віднімання застосовуються різноманітні демонстраційні абаки (мал. 11, 12). Індивідуальні абаки (мал. 13) побудовані так само, як демонстраційні (мал. 12). 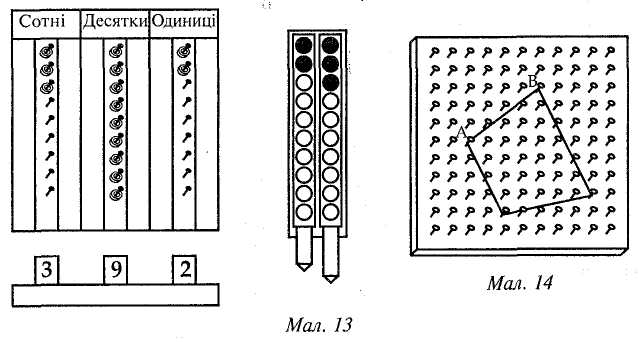 Велике значення в навчанні математики мають моделі і набори геометричних фігур. Значну частину задач геометричного змісту можна відтворити на посібнику, який являє собою дошку (фанеру) із вбитими в неї гвіздками на відстані 5 см один від одного (гвіздки над поверхнею дошки виступають на 1—2 см) (мал. 14). Для роботи з посібником використовують кольорові гумки. За допомогою такого посібника можна швидко відтворювати, змінювати геометричні фігури, розв'язувати як прості, так і складені задачі геометричного змісту. До технічних засобів навчання математики належать кінопроектори, діапроектори, епідіаскопи, кодоскопи. Вони допомагають у багатьох випадках замінити записи на класній дошці під час пояснення вчителем нового матеріалу. Найпоширенішими серед різних екранних засобів навчання є діафільми. Вони розраховані на вивчення учнями нового матеріалу і служать ілюстрацією до пояснення. Окремі фрагменти можуть бути використані на етапах закріплення, повторення й узагальнення знань та з метою контролю знань, умінь і навичок. Діапозитиви — це своєрідні окремі кадри діафільму. Проте вони можуть бути виготовлені самим учителем. На плівку наносяться потрібні записи чи малюнки. Діапозитиви демонструють за допомогою епідіаскопа. Кодоскоп поєднує в собі можливості класної дошки і діапроектора. Матеріал для кодоскопа, як і для епідіаскопа (епікадри і епістрічки), за змістом і художнім оформленням може добирати і виготовляти сам учитель. Розділ III. Засоби навчання математики в початкових клас 40 У 3—4 класах учням варто показати застосування комп'ютера для розв'язування задач. Під час підготовки до уроку з використанням технічних засобів навчання слід визначити місце і час демонстрації екранного посібника; зазначити місце зупинок для проведення бесіди, самостійної або інших видів роботи, а також місця, коли треба дати додаткові пояснення під час демонстрації екранного посібника; продумати зміст цих пояснень. §11. Засоби зворотного зв'язку Виконуючи завдання з усних обчислень, учні піднімають руку і з дозволу вчителя усно повідомляють відповідь. Нерідко вчителі пропонують дітям показати відповіді за допомогою розрізних цифр. Це допомагає залучати до роботи всіх учнів, а вчитель бачить, як діти впорались із завданням. Застосування розрізних цифр зручне для випадку дій у межах 10. За межами десятка повідомлення відповідей за допомогою розрізних цифр дещо ускладнюється. Тому в практиці розроблені й інші засоби зворотного зв'язку. Розглянемо деякі з них. Віяло (мал. 15). Розрізні цифри скріплені у вигляді віяла. 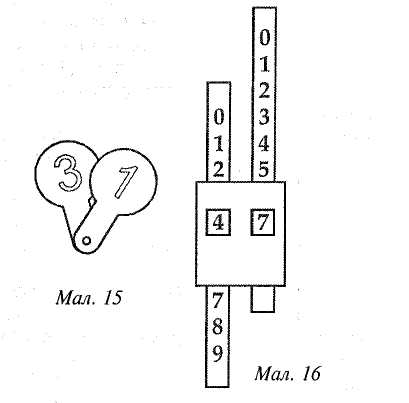 Числовий абак (мал. 16). Цей пристрій складається з двох стрічок, на кожній з яких записані одноцифрові числа. Вони можуть рухатись у картонній рамці. У рамці зроблені віконця для чисел. Для повідомлення відповіді, наприклад 47, учень має розмістити стрічки так, щоб це число з'явилося в рамочці. Методика викладання математики в початкових класах 41 Таблиця чисел першої сотні. Числа першої сотні записують на подвійному аркуші з учнівського зошита: у першому рядку числа 1—10, у другому — 11—20 і т. д. Висота цифри 17 мм. На зворотному боці всі числа можна записати висотою в одну клітинку. Малі цифри записують навпроти відповідних великих. Повідомляючи відповідь, учень піднімає аркуш і паличкою (олівцем, ручкою) показує потрібне число. Таблиця 8 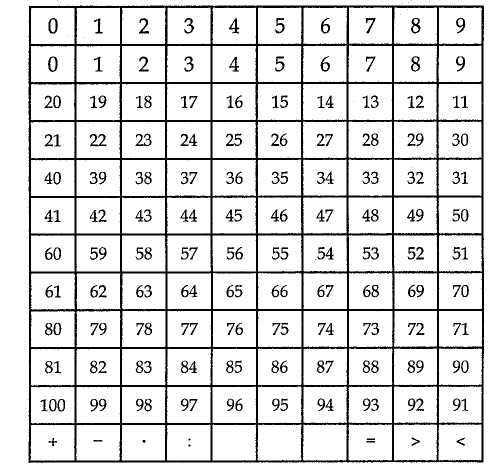 Кодування відповіді. Для швидкого оцінювання правильності відповіді достатньо, якщо учень повідомить не саму відповідь, а стовпчик, в якому є шукане число. У такому разі учневі достатньо мати тільки розрізні цифри. Для кодування відповіді можна також використати таблицю чисел першої сотні (табл. 8). Ця таблиця доповнена верхнім рядком (цифровим кодом) і нижнім рядком (для знаків арифметичних дій і знаків порівняння). Числа в таблиці записані "змійкою". Нехай учні 2-го класу виконали такі завдання: 57+14 = 71(9) 51-17 = 34(6) З • 7 = 21 (0) 36 : 4 = 9 (8) Учні записують відповідь, а поряд у дужках кодовані відповіді. На прохання вчителя вони показують кодовані відповіді цифрами. Цифра 9 означає, що шукана відповідь (71) знаходиться у дев'ятому стовпчику. РОЗДІЛ IV СКЛАДОВІ ЧАСТИНИ УРОКУ МАТЕМАТИКИ. МЕТОДИ ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ Урок математики — основна форма організації навчальної діяльності молодших школярів. В уроці реалізується освітня, виховна та розвивальна мета навчання математики. Освітня мета полягає в засвоєнні учнями математичних понять та у формуванні в них специфічних для математики вмінь і навичок. У початковій школі учні засвоюють елементарні математичні поняття про число і дії, задачу, величини і вимірювання, про геометричні фігури. Крім математичних, формуються також загальнотрудові знання, вміння і навички. До них належать: організаційні (опанування способів організації свого навчання, зокрема вміння планувати роботу і користуватися підручником); загальнопізнавальні (вміння спостерігати, міркувати, запам'ятовувати і відтворювати матеріал); загальномовленнєві (основні елементи культури слухання і мовлення); контрольно-оцінні (засвоєння способів перевірки та самоперевірки, оцінювання здобутих результатів). Виховна мета передбачає формування в учнів уявлення про світ загалом, місце людини в ньому і способи його пізнання; вказує загальні орієнтири засвоєння нагромадженого людством соціального досвіду, магістральні шляхи перетворення дійсності. У процесі навчання математики виховуються вольові якості людини: наполегливість у доведенні справи до кінця, охайність, самостійність, кмітливість, ініціативність. Розвивальна мета полягає в тому, щоб добитися розвитку в учнів пізнавальних здібностей (сприймання, пам'яті, уяви, мови), мотивів і потреб навчання, творчих можливостей, емоційної сфери. У педагогіці визначено такі вимоги до уроку: його чітка цілеспрямованість, теоретична й практична повноцінність змісту; правильне застосування та поєднання різних форм організації пізнавальної діяльності учнів (класної, групової, індивідуальної); виразне формулювання основних висновків; достатнє закріплення і повторення нового матеріалу; оперативне з'ясування лупеня оволодіння знаннями. Для ефективного уроку математики характерні такі особливості: широке застосування фронтальних форм перевірки знань, надання опитуванню навчального спрямування, поєднання функцій контролю і закріплення; Методика викладання математики в початкових класах 43 проведення на уроці самостійної роботи, спрямованої на оволодіння новим матеріалом; посилення ролі первинного закріплення, збільшення обсягу практичних робіт і тренувальних вправ. На кожному уроці передбачені встановлення свідомої трудової дисципліни, живе спілкування з учнями, емоційне мотивування навчальної діяльності школярів. За основною дидактичною метою виділяють такі типи уроків: 1)урок засвоєння нових знань; 2) урок засвоєння навичок і вмінь; 3)урок застосування знань, навичок і вмінь; 4) урок узагальнення і систематизації знань; 5) урок перевірки, оцінювання і корекції знань, умінь і навичок; 6) комбінований урок. У початкових класах немає уроків, повністю присвячених вивченню нового матеріалу. Новий матеріал невеликими частинами розглядають майже на кожному уроці. Тому найпоширенішими в початкових класах є комбіновані уроки. Комбінований урок містить такі компоненти: 1) перевірка домашнього завдання; 2) опитування учнів; 3) усні обчислення; 4) підготовка до вивчення нового матеріалу і повідомлення теми заняття; 5) опрацювання нового матеріалу; 6) первинне закріплення; 7) закріплення й повторення; 8) домашнє завдання та підбиття підсумків уроку. У структурі комбінованого уроку його компоненти можна об'єднати в такі три частини: 1. Контроль, корекція та закріплення знань учнів (перевірка домашнього завдання, опитування учнів та усні обчислення). 2. Опрацювання нового матеріалу (підготовка до вивчення нового матеріалу, його вивчення та первинне закріплення). 3. Закріплення та узагальнення знань учнів (закріплення і повторення матеріалу, завдання додому, підбиття підсумків уроку). Цю частину часто називають "розвиток математичних знань учнів". Розгляд окремих частин і компонентів комбінованого уроку подаємо в наступних трьох параграфах. У решті параграфів цього розділу розглянемо інші різновиди уроків, форми навчальної діяльності учнів і нормативи оцінювання їхніх знань. §12. Контроль, корекція та закріплення знань учнів Компоненти першої частини уроку — перевірка домашньої роботи, опитування учнів і усні обчислення — взаємопов'язані. Ці компоненти уроку використовують як для контролю, так і для закріплення знань. Нерідко їх важко розрізнити, визначити момент переходу від одного до іншого. Проте кожний зі згаданих видів робіт має свою специфіку, тому методику проведення кожного з них розглядатимемо окремо. Перевірка домашньої роботи Щоб цей вид навчальної роботи був справді корисним і ефективним, потрібно звертати увагу на активізацію діяльності учнів під час перевірки Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 44 домашньої роботи. Виконувати перевірку треба швидко, чітко, часто змінюючи форму. Ні в якому разі не можна погодитися з учителями, які вважають, що перевіряти в класі домашні завдання не варто, оскільки вчитель перевіряє зошити. Якщо не перевіряти домашні завдання, то втрачається виховне значення роботи. Щоб перевірка не перетворювалась на нудну для школярів роботу, треба уникати одноманітності в її проведенні. Залежно від мети уроку і змісту домашнього завдання перевірка може бути повною, вибірковою або зводитись до констатування самого факту, що завдання виконано. Форми перевірки чергуються протягом тижня. Причому повна і вибіркова перевірки, як правило, поєднуються з опитуванням учнів та з усними обчисленнями. Повна перевірка займає 5 — 6 хв уроку і найчастіше проводиться так: один-два учні записують, користуючись підручником, розв'язання задач або обчислення виразів на дошці. Інші в цей час вправляються в усних обчисленнях або під керівництвом учителя перевіряють правильність обчислення решти виразів. Варто запропонувати дітям прочитати один з виразів з повним поясненням способу обчислення. Потім увага учнів звертається на записи, що є на дошці. Той, хто записав розв'язання задачі, коротко повторює її умову, повідомляє план її розв'язання і повну відповідь. Весь клас перевіряє розв'язання задачі на дошці, кожний має звірити відповідь зі своєю. Відповідно до запису розв'язання задачі на дошці, вчитель нерідко ставить одне-два запитання для уточнення якості роботи. Потім він дає додаткові завдання (необов'язково за темою домашнього завдання) і виставляє учню оцінку. Під час вибіркової перевірки звертається увага на задачі і вправи, що важливі для усвідомлення теоретичного матеріалу даного уроку. Тренувальні завдання в цей час перевіряють побіжно — читають лише відповіді. Для вибіркової перевірки достатньо 3-5 хв уроку. Вчитель пропонує спочатку одному-двом учням підготувати матеріал для перевірки: записати на дошці розв'язання певних прикладів або задачі повністю чи частково, але щоб було достатньо даних для пояснення та коментування вправи. Поки діти готують записи, класовод фронтально опитує решту дітей. Вибіркову перевірку можна проводити усно. У такому разі школярі відповідають з місця, користуючись записами в зошитах. Наявність виконаного завдання вчитель з'ясовує, переглядаючи учнівські зошити на партах. (У цей час діти можуть бути зайняті взаємоперевіркою — вони перевіряють правильність розв'язання завдань один в одного). Тут доцільно поставити два-три запитання щодо окремих місць у розв'язанні задач і обчисленні виразів. У 3-4 класах перевірку наявності виконаного завдання можна доручати учням. Відповідальні за цю роботу на початку уроку переглядають зошити учнів свого ряду, потім доповідають учителеві про результати перевірки. Така форма має певне виховне значення: діти відчувають більшу відповідальність перед товаришами, перед колективом за свою роботу вдома. Оскільки ця перевірка короткочасна (1—2 хв), то після неї іноді доцільно проводити п'яти-, семихвилинну самостійну роботу, близьку за змістом до домашньої. На конкретних зразках розглянемо деякі прийоми перевірки домашньої роботи, що сприяють підвищенню активності учнів, розвитку їхньої Методика викладання математики в початкових класах 45 самостійності, допомагають зекономити час на уроці. Реалізація таких прийомів найчастіше проводиться на основі попередніх записів на дошці. Перевірка обчислення виразів 1. Перед уроком записати на дошці обчислення виразів домашнього завдання (усіх або кількох). За цими записами учні перевіряють правильність своїх відповідей. 2. Записати на дошці числові значення виразів (у порядку зростання). Учні звіряють їх зі своїми результатами. 3. Записати на дошці вирази. Один-два або кілька учнів по черзі виходять до дошки і записують значення виразів. 4. На дошці записано рівності, одна-дві з них неправильні. Учні знаходять помилки і виправляють їх. 5. Учитель пропонує дітям додати значення всіх виразів і результат порівняти з числом, записаним на дошці (це число і є сумою значень виразів). 6. На дошці подано розгорнутий запис обчислення виразу. За допомогою такого запису треба пояснити хід розв'язування і вказати, на які властивості дій спирається застосований обчислювальний прийом. 7. Перевірити обчислення виразів такими методами: повторно пояснивши хід розв'язування; переставивши доданки чи множники; застосувавши зв'язок між арифметичними діями. 8. На дошці подано записи письмового множення чи ділення. Назвати всі неповні добутки або неповні ділені. 9. Розповісти про порядок виконання дій у виразі з дужками або на сумісні дії першого і другого ступенів. 10. Назвати компоненти і результат одного-двох виразів, наприклад, 84: 21 = 4; 84 — ділене, 21 — дільник, 4 — частка. 11. Прочитати кількома способами рівності, наприклад, 73 - 19 = 54 (від числа 73 відняти 19, буде 54; 73 мінус 19 дорівнює 54; 73 зменшити на 19, буде 54; зменшуване — 73, від'ємник — 19, різниця — 54; 73 більше від 19 на 54). Перевірку розв 'язання задані можна провести так: 1. На дошці записано розв'язання задачі. Учні звіряють з ним свої записи. 2. Учитель або учень записує на дошці числовий вираз розв'язання задачі або окремі дії, а діти повідомляють план розв'язання і повну відповідь. 3. На дошці записано числові відповіді до кожної задачі. Учні мають звірити їх зі своїми, а потім прочитати повні відповіді. 4. Учитель записує план розв'язання задачі, а учні повинні записати дії, за допомогою яких цей план реалізується. 5. Розповісти, яка залежність існує між величинами, даними в задачі. 6. Один з учнів читає задачу і розповідає, як її слід розв'язувати. Після цього вчитель пропонує записати на дошці числовий вираз або окремі дії розв'язання за умови, що одне з даних задачі змінено. Наприклад, у задачі йшлося про купівлю 6 м тканини; змінити це число на 9 м. 7. Складену задачу перетворити на окремі прості задачі. 8. Скласти задачу аналогічну (обернену, з іншими запитаннями тощо) до тієї, яка розв'язувалася вдома. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 46 9. Порівняти розв'язання задачі з домашньої роботи із задачею, яка розглядалася раніше. Класоводи нерідко показують учням кращі зразки виконання домашнього завдання. Школярам, роботи яких демонструються як кращі, варто виставляти відмінну оцінку в класному журналі. Взагалі доцільно відповіді здного-двох учнів на уроці в процесі пояснення виконання домашніх завдань оцінювати в балах. Усне опитування Усне опитування — одна з форм динаміки вивчення успішності учня. Опитування передбачає: контроль і перевірку знань, умінь і навичок учнів; закріплення та поглиблення вивченого матеріалу; підготовку до сприймання нових знань. Сучасна дидактика привертає увагу до творчого (осмисленого) зідтворення навчального матеріалу в процесі перевірки знань. Такий підхід змінює співвідношення контрольної і навчальної функцій перевірки, вона ;тає засобом поглиблення та засвоєння знань, розвитку мислення учнів. Облік успішності молодших школярів з математики не становить для вчителя значних труднощів. Проводячи кожного семестру чотири-п'ять письмових контрольних робіт, оцінюючи певну частину письмових самостійних робіт (класних і домашніх), учитель має достатньо чітку картину стану засвоєння тієї чи іншої теми та рівня сформованості вмінь і навичок учнів. Це створює передумову для посилення навчальної функції індивідуального опитування. Навчальні резерви опитування доцільно спрямовувати на посилення пізнавальної активності учнів класу, зокрема на усвідомлення програмового матеріалу тими учнями, які відстають у навчанні. ' Усне опитування має бути стимулюючим у навчанні школярів. Його потрібно проводити систематично й послідовно, застосовуючи індивідуальний підхід до учнів, розвиваючи в них самоконтроль, зацікавленість у перевірці знань і оцінюючи їхні знання. Для поточного опитування треба добирати такий матеріал, який ще потребує закріплення й узагальнення. Якщо спиратися на матеріал, яким ііти оволоділи досконало, то в класі спостерігатиметься лише зовнішня іктивність, учні працюватимуть без достатнього розумового напруження. Педагогічний такт, об'єктивна вимогливість учителя, що поєднується з його Зажанням допомогти кожному учневі, сприяють вихованню в дітей пра-зильного ставлення до обліку їх успішності. Неприпустимим є виставлення пезадовільної оцінки за випадкову неуважність, забутий вдома зошит або нші порушення дисципліни. Важливе значення має добір матеріалу для опитування. Наведемо перелік теоретичного матеріалу, вмінь і навичок у виконанні математичних завдань, оівень засвоєння яких учнями має перевіряти вчитель. 1. Знання таблиць арифметичних дій. (У кінцевому результаті таблиці вдцавання, віднімання, множення і ділення учні повинні засвоїти напам'ять). Уміння самостійно скласти ту чи іншу таблицю додавання або віднімання па основі предметної ситуації чи застосування прийому обчислення, таблицю иноження на основі означення дії множення і таблицю ділення на основі ззаємозв'язку дій множення і ділення. Методика викладання математики в початкових класах 47 2. Уміння усно виконувати арифметичні дії в межах 100 та над круглими числами в межах 1000. Знання основних (загальних) прийомів позатабличного виконання арифметичних дій. 3. Знання алгоритмів письмового виконання арифметичних дій. Уміння письмово виконувати обчислення над багатоцифровими числами. 4. Знання теоретичного матеріалу: побудова натуральної послідовності чисел, принципи усної і письмової нумерації чисел (групування чисел у розряди і класи, помісцеве значення цифр), властивості арифметичних дій, взаємозв'язку між компонентами і результатами арифметичних дій, порядок виконання дій у виразах без дужок і з дужками. 5. Знання одиниць вимірювання величин (довжини, маси, часу, площі); позначення одиниць вимірювання; знання відношень між одиницями вимірювання однієї і тієї самої величини. Уміння подавати значення величини в різних одиницях вимірювання. 6. Уміння розв'язувати прості і складені задачі, зміст і складність яких визначаються матеріалом діючих підручників. 7. Уміння обчислювати вирази на 2—4 дії; знаходити числові значення виразів з буквеними даними; знаходити дріб від числа та число за його частиною; розв'язувати рівняння (на одну операцію). 8. Знання таких геометричних фігур, як: точка, пряма лінія, відрізок, многокутники, коло. Уміння розпізнавати ці фігури та їх елементи. Уміння вимірювати та будувати відрізки заданої довжини, будувати прямокутник на папері в клітинку та вимірювати його площу. Щоб усунути випадковість у доборі запитань і завдань для опитування, контролювати частоту їх постановки, варто до кожної великої теми наперед (перед опрацюванням на уроках) сформулювати і записати можливі запитання і основні завдання. Це стане у нагоді під час підготовки до кожного окремого уроку. Добір завдань для опитування з кожної теми у кожному класі — відповідальна й копітка справа. У процесі вивчення математики застосовується індивідуальне і фронтальне опитування. У першому випадку учень виконує завдання на дошці і відповідає перед класом на поставлені йому запитання. У другому випадку вчитель пропонує завдання всьому класу і на них відповідають кілька учнів. Індивідуальне опитування. Усне опитування біля дошки практикується майже на кожному уроці. Таким способом на одному уроці варто опитувати одного-двох учнів. Першому учневі завдання і запитання для опитування вчитель повідомляє вголос. Ці завдання, як правило, виконують всі діти класу. Бажано, щоб відповіді були наближені до зв'язного пояснення. Учень пояснює виконані обчислення, відповідає перед класом на поставлені запитання. Учні класу перевіряють правильність обчислення, за пропозицією вчителя уточнюють відповіді. Другий учень працює біля дошки самостійно за завданнями, записаними на картці. Залучати усіх дітей до перевірки правильності виконання ним завдань необов'язково. Учитель здебільшого сам перевіряє правильність виконання і виставляє оцінку. В разі необхідності він дає учневі додаткові запитання. Об'єктивність оцінки й активність дітей у процесі усного опитування значною мірою залежать від обсягу і змісту поставлених завдань. Здебільшого одне із Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 48 завдань чи запитань стосується матеріалу попереднього уроку, а інше — даної теми. Бажано, щоб від уроку до уроку спостерігалася певна наступність завдань. Фронтальне опитування. У початкових класах фронтальне опитування подібне до усних обчислень. Проте його можна розглядати і як самостійний вид навчальної роботи. Опитування проводиться у формі бесіди. Подамо зразок завдань і запитань для опитування на один урок (під час вивчення таблиці ділення на 7). 1) Посіяли 4 кг вівса, а зібрали 36 кг. У скільки разів більше кілограмів вівса зібрали, ніж посіяли? 2) За 2 год трактор витратив 14 л пального. Скільки літрів пального йому потрібно для 8 год роботи? 3) Розкажіть (по черзі) таблицю множення числа 7. 4) Розкажіть всю таблицю множення числа 7 (одному учневі). 5) Які приклади на ділення можна скласти за прикладом 5 • 6 = ЗО? 6) Що отримаємо, коли добуток двох чисел поділимо на перший множник? Наведіть приклад. На фронтальне опитування відводиться 5 — 8 хв. Відповідають багато учнів. Одного-двох школярів учитель викликає для відповідей 2 — 3 рази. Цим учням виставляють оцінки. У початкових класах не слід ставити суворі вимоги в процесі усного опитування. Перш ніж контролювати знання учня, треба його озброїти цими знаннями. Розглянемо детальніше прийоми навчаючого опитування. Сутність таких прийомів розкриємо на конкретних зразках завдань з основних тем програми. Прийом типових структур. Опитування проводиться за тими наочними посібниками або структурними записами (схемами, таблицями, малюнками), які використовував учитель для пояснення нового матеріалу. Ці посібники чи записи одразу вводять учнів у проблему завдання, а кількаразове використання їх перетворює на своєрідні еталони. Відповіді за допомогою типових структур не сприятимуть механічному заучуванню, оскільки завжди можна запропонувати дітям навести власні приклади. Тема опитування. Складання таблиці додавання числа 7 і віднімання числа 7. На набірному полотні — ряди кружечків для складання таблиць додавання і віднімання числа 7 в межах 10 (мал. 17). 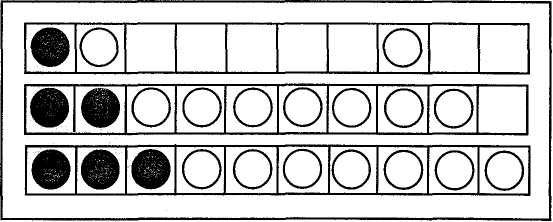 Мал. 17 Методика викладання математики в початкових класах 49 1. Розгляньте малюнки і поясніть, як за ними можна скласти таблицю додавання числа 7. Зразок пояснення. У першому рядку 1 чорний кружечок і 7 білих. Можна скласти приклад: 1 + 7. Полічимо, скільки всього кружечків: один, два, три, чотири, п'ять, шість, сім, вісім. Отже, 1+7 = 8. 2. Прочитайте таблицю додавання числа 7. 3. Поясніть, як за малюнками склали таблицю віднімання числа 7. Зразок пояснення. У третьому рядку всього 10 кружечків, з них 7 білих, а решта чорні. Можна скласти приклад: 10 — 7. Якщо віднімемо білі кружечки, то залишаться 3 чорних кружечки. Отже, 10 — 7 = 3. 4. Прочитайте таблицю віднімання числа 7. Прийом наочно-практичних дій. З погляду "навчаючого опитування" наочно-практична форма постановки завдань має великі переваги. Тема опитування. Додавання і віднімання в межах 6. 1. За допомогою 6-ти паличок складіть і запишіть всі приклади на додавання з відповіддю 6. 2. Користуючись паличками, знайдіть відповіді до прикладів: 6-1 6-2 6-3 6-4 6-5 Прийом підказування. Завдання для опитування поділяються на дві частини. Перша, як правило, будується на наочній основі (запис на дошці, малюнок, таблиці). Це полегшує сприймання дітьми самого завдання, привертає їх увагу до проблеми і певною мірою є підказкою для знаходження відповіді. Відповіді на запитання і вправи другої частини покажуть учителеві, чи свідомо учні засвоїли матеріал, чи вони вміють застосовувати знання в дещо зміненій ситуації. Тема опитування. Порядок виконання арифметичних дій. 1. Прочитайте приклад 3 + 7 • 4 і поясніть, в якому порядку виконували дії. 2. Розв'яжіть приклади: 28 — 8 : 4; (28 - 8): 4. 3. В якому порядку треба виконувати дії у виразах без дужок? Прийом опитування за планом застосовується під час закріплення чи узагальнення знань з тієї чи іншої теми. Цей прийом є особливо зручним для закріплення алгоритмів виконання арифметичних дій. Опитування проводиться за допомогою конкретних завдань, зміст яких записують на дошці. План пояснення (послідовність запитань) подано на картці. Запитання плану охоплюють основні (істотні) питання теми (математичного поняття чи алгоритму виконання арифметичної дії). Запитання формулюються так, щоб планом можна було скористатися кілька разів (замінивши тільки числа чи інші математичні поняття). Учень, якого опитують, ознайомлюється з конкретним завданням і планом, а в разі потреби самостійно виконує потрібні обчислення. Завершальний етап (основний щодо навчальної функції) пояснення чи розповідь за планом: учитель (часом учень) читає вголос пункти плану, а викликаний учень відповідає. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 50 Тема опитування. Позатабличне множення і ділення. Завдання. Розв'язати приклади: 80 : 10 3-27 52 : 2 18-4 72 : 12 64 : 4 Розповісти про виконання обчислення за планом: 1. Який з виразів можна обчислити за правилом множення суми на число? 2. При обчисленні якого виразу зручно було застосувати переставну властивість дії множення? 3. Які частки знаходимо за правилом ділення суми на число, а які — випробовуванням? 4. Як перевірити результат ділення дією множення? Наведіть приклад. 5. Складіть самостійно приклад, що розв'язується за правилом ділення суми на число. Тема опитування. Розпізнавання прямокутників і квадратів. Розгляньте многокутники і розкажіть про них за планом (мал. 18). 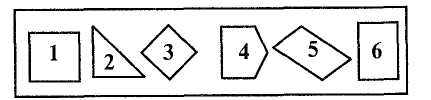 Мал. 18 1. Скільки всього прямокутників на малюнку? Якими цифрами їх позначено? 2. Якими цифрами позначено квадрати? Який прямокутник називається квадратом? 3. Покажіть сторони і вершини одного з прямокутників. Прийом типових помилок і провокуючих вправ. Знаходячи помилку в розв'язаних завданнях і пояснюючи її причину, учні стають уважнішими. Щоб цей прийом став навчальним, треба пропонувати дітям приклади з типовими помилками: сплутування розрядів під час додавання чи віднімання, пропуск нулів у частці, неправильне розміщення чисел при письмовому виконанні дій та ін. Якщо помилку допустив учень, якого опитують, і її можна конкретизувати, то це треба зробити. Наприклад, учень повідомив: "Щоб помножити число на 100, треба до нього дописати 2 нулі". Для конкретизації неточності вчитель записує на дошці: 17 • 100 = 0017. "Провокуючими" умовно назвали такі завдання, які спрямовують учнів на виконання їх не за правилом, а "легшим" способом, що призводить до помилки. Наприклад, 14 + 6 • 3, х - 6 = 26, 48 016 : 16. Доцільно урізноманітнювати форми опитування. Однією з них є "парне" опитування. До дошки викликають двох учнів, і вони по черзі відповідають. Завдання, як правило, пов'язані між собою. Для урізноманітнення опитування учнів бажано використовувати перфокарти, подачу завдань через графопроектор, на магнітній дошці. Методика викладання математики в початкових класах 51 |
