методика математики книга. Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.58 Mb. Скачать 4.58 Mb.
|
|
§16. Форми організації навчання учнів математики на уроці Навчання учнів математики на уроці організовують у формі колективної фронтальної або індивідуальної самостійної роботи, застосовують також і групову форму навчання. Колективна форма роботи має характер бесіди вчителя й учнів з елементами зв'язного пояснення. В роботі над конкретним математичним матеріалом бесіда використовується на різних етапах його опрацювання. Особливою формою фронтальної роботи є така, коли учитель сам ставить запитання і сам відповідає на них (за суттю це метод зв'язного викладу, розповіді). Застосування такої форми в початкових класах доцільне, оскільки молодші школярі великою мірою у навчанні наслідують учителя. Коментоване розв'язування завдань учителем призначене найчастіше не для ознайомлення з новим матеріалом, а для подання учням зразків міркування. У практиці навчання є багато ситуацій, коли необхідно, щоб те саме завдання діти розв'язали одночасно із записом його розв'язання на дошці. Це напівсамостійна робота: один з учнів розв'язує завдання на дошці або коментує розв'язання з місця, а решта розв'язує його в зошитах. Звичайно, вчитель рекомендує дітям працювати самостійно, але учень у будь-який час може побачити запис розв'язання чи почути пояснення ходу розв'язування і звірити його зі своїм. Напівсамостійна форма роботи може бути застосована: а) у процесі первинного закріплення, тобто під час розв'язування перших після показу Методика викладання математики в початкових класах 89 вчителем завдань на ознайомлення з новими поняттями чи новими видами задач; б) під час розв'язування завдань підвищеної складності; в) для порівняння різних способів розв'язування того самого завдання; г) для аналізу помилок, допущених учнями під час самостійного розв'язування завдань; г) у ході підготовки дітей до сприймання нового матеріалу, в тому числі задач нового виду. Індивідуальна самостійна робота передбачає розв'язування завдання кожним учнем окремо. Вона застосовується на будь-якому з етапів навчання, але найчастіше в процесі розвитку вмінь виконувати завдання того чи іншого виду. Самостійне розв'язування завдань у початкових класах майже завжди для учнів є творчим процесом. Отже, в організації такої роботи слід враховувати вимоги щодо проблемного навчання. Вчитель спрямовує дітей на самостійне розв'язування завдань за допомогою відповідних підготовчих вправ або засобів унаочнення, своєчасно виявляє помилкові міркування учнів у процесі розв'язування завдань і допомагає їм, підтримує при цьому емоційний тонус і впевненість у тому, що кожен з учнів спроможний самостійно розв'язати завдання. В організації діяльності учнів щодо розв'язування того чи іншого завдання ичитель завжди ставить певну мету і залежно від неї визначає форму роботи. Зрозуміло, що колективна й індивідуальна форми роботи можуть змінюватись навіть у процесі виконання одного завдання. Наприклад, ознайомлення зі змістом задачі було проведено у формі колективної фронтальної роботи, а аналіз задачі, складання плану і її розв'язування вчитель пропонує здійснити самостійно. Практикуються також групові форми навчання. Здебільшого це парні, ланкові або диференційовано-групові. У початкових класах найчастіше використовують диференційовано-групову форму, що передбачає організацію роботи груп з різними навчальними можливостями. Найчастіше учнів поділяють натри групи: сильнішу, середню і слабку. За диференційовано-груповою формою навчання всі діти здебільшого працюють за завданнями, що мають спільну пізнавальну мету. Для різних за навчальними можливостями груп учнів завдання відрізняються за обсягом, рівнем складності, мірою допомоги. Під час ознайомлення, наприклад з новою задачею, застосовують два способи диференціації. За першим способом диференційовану роботу організовують у комплексі з фронтальною. Ознайомлення зі змістом нової задачі проводиться фронтально. Наявність різних груп учнів учитель враховує під час первинного закріплення матеріалу. Діти першої і другої груп працюють самостійно за картками або з підручником. З учнями третьої групи вчитель повторно аналізує задачі, розглядає окремі питання, в яких висвітлюється суть задачі, її новизна. За другим способом учням першої групи надається можливість спробувати самостійно розв'язати задачу нового типу. Вчитель повідомляє мету роботи. Потім роздає їм картки з текстами задач нового виду, а з учнями другої і третьої груп працює над задачами фронтально. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 90 Організовуючи самостійну роботу учнів, найчастіше застосовують такі три види диференціації: індивідуалізацію вимог до спільного завдання; надання допомоги в одному з варіантів самостійної роботи (індивідуальна допомога); спрощення одного з двох варіантів самостійної роботи. Індивідуалізація вимог до спільного завдання. Для всіх учнів учитель записує на дошці або вказує в підручнику одне й те саме завдання, але інструкція його виконання передбачає й деякі прийоми диференціації. Вимоги до розв'язання завдань. Усім учням пропонується, наприклад, та сама задача, причому одразу подається й додаткове завдання щодо цієї задачі. Такими додатковими завданнями можуть бути: розв'язати задачу іншим способом; скласти вираз за розв'язанням задачі окремими діями; змінити запитання й знайти на нього відповідь, скласти подібну задачу; скласти і розв'язати обернену задачу, записати план розв'язування задачі та ін. Якщо учням пропонується вправа, наприклад на обчислення виразів, то додатковими завданнями можуть бути: знайти значення виразу іншим способом, всіма можливими способами; записати подібний вираз і обчислити його значення; обчислити значення виразів і записати їх значення в зростаючому (спадному) порядку та ін. Постановка кількох запитань до умови задачі. Вчитель записує на дошці умову задачі і до неї 2—3 запитання. Кожен учень знаходить відповідь на стільки запитань, на скільки зможе. Зрозуміло, що бажано відповісти на всі запитання. Додаткове завдання, не пов'язане з основним. Учитель зазначає: "Учням, які першими розв'яжуть завдання, треба спробувати виконати ще й додаткове". Ним може бути: обчислення виразів, розв'язування нової задачі, а найчастіше — завдання з логічним навантаженням. Робота над додатковим завданням припиняється одразу, як тільки вчитель організує учнів на інший вид діяльності. Дітям, які не встигли чи не змогли виконати додаткове завдання, пропонується подумати над ним вдома. Невиконання його не впливає на оцінку роботи учня. Індивідуальна допомога. Завдання для самостійної роботи пропонується у кількох варіантах. В одному чи двох з них міститься додаткова інформація, розрахована на допомогу в розв'язуванні задач. Реалізується цей вид диференціації найчастіше через індивідуальні картки. Розгляньмо прийоми допомоги. Конкретизація задачі. До задачі додається малюнок або її короткий запис. Задача. Довжина першої смужки 10 см, а другої — 8 см. На скільки сантиметрів довша перша смужка від другої? (Мал. 28). 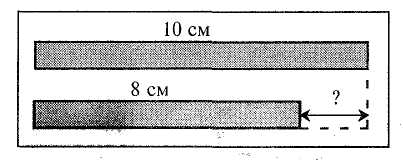 Мал. 28 Методика викладання математики в початкових класах 91 Прочитати задачу, розглянути до неї малюнок і обґрунтувати дію, якою вона розв'язується. Розв'язання записати в зошит. Повідомлення відповіді до задачі або числових значень виразів. Коли розв'язують задачу на 2-3 дії або знаходять значення виразу, то знання відповіді допомагає аналізувати хід роботи. Знаючи відповідь, учень самостійно виправляє допущену помилку. Навідні вказівки чи запитання. Вказівки безпосередньо пов'язані з конкретним змістом задач, але взагалі вони бувають на зразок таких: це задача на три дії; для розв'язання задачі буде потрібно виконати дію віднімання, а потім дію множення; подумай, як знайти ціну за вартістю і кількістю товару; будь уважний: блокнотів купили стільки, скільки зошитів; якою дією дізнаємось, у скільки разів одне число більше від іншого? Початок розв'язування завдання, задачі. У картці подається виконання першої дії або початок аналізу числових даних і запитання для першої дії. Задача. Якщо шматок дроту розрізати на 4 частини по 16 му кожній, то залишиться ще 6 м. Однак дріт розрізали на частини по 5 м у кожній. На скільки частин розрізали дріт ? Аналіз. Щоб знайти відповідь, треба знайти довжину всього шматка дроту. Знайдемо довжину за першою частиною умови. Залишилося 6 м. Отже, потрібно ще знайти, скільки метрів дроту розрізали на 4 частини. Закінчити аналіз задачі, скласти план її розв'язування і розв'язати. Зразок розв'язання. На картці подано дві задачі одного виду, одна з яких вже розв'язана. /. Доярка надоїла 96 л молока. 16 л вона віддала телятам, а решту розлила порівну в 4 бідони. Скільки літрів молока доярка налила в один бідон? 1)96— 16 = 80(л); 2)80: 4 = 20(л). Відповідь. 20 літрів. 2. Виготовили 40 л томатного соку. 13 л соку вилили в сулію, а решту розлили порівну в 9 банок. Скільки літрів соку налили в одну банку? Перевірити розв'язання першої задачі та розв'язати другу. Подання пояснень чи плану розв'язування задачі. Задача. На першій ділянці посадили 240 сосен по 20 сосен у кожному ряду, а на другій — 360 акацій по 40 акацій у кожному ряду. На скільки рядів сосен більше, ніж рядів акацій? Рядів сосен ... Рядів акацій ... Більше рядів сосен, ніж рядів акацій на ... Заповнити пропуски потрібними виразами, виконати обчислення і записати повну відповідь до задачі. Подання схеми розв'язування чи графічного зображення результату аналізу задачі. 1. На складі було 48 березових і 36 соснових колод. На дошки розпиляли всі березові колоди і четверту частину соснових. Скільки всього колод розпиляли на дошки ? Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 92 Користуючись схемою, розв'язати задачу, склавши вираз. 2. У магазин привезли 70 кг груш і 3 ящики яблук по 15 кг у кожному. Скільки кілограмів фруктів привезли? Розв'язати задачу, користуючись вказівками. На мал. 29 показано, що першу дію треба виконувати над даними числами 15 і 3, а другу — над знайденим числом і числом 70. 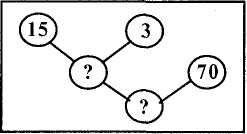 Мал. 29 Подання інформації, потрібної для розв'язування завдання. Такою інформацією є правила, тлумачення залежностей між величинами та ін. Наприклад: а) щоб знайти невідоме зменшуване, до різниці слід додати від'ємник; б) щоб за відомою площею прямокутника і його довжиною знайти ширину, треба площу поділити на довжину; в) щоб скласти обернену задачу, потрібно одне з даних (яке саме?) вважати невідомим. Задача. У минулому році з дослідної ділянки зібрали 14 ц 4 кг ярої пшениці. У цьому році посіяли новий сорт пшениці і з тієї самої ділянки зібрали на 1/6 більше всієї маси пшениці, ніж у минулому. Скільки кілограмів пшениці зібрали з ділянки в цьому році? Вказівка. Щоб знайти шосту частину числа, треба це число поділити на 6. Наведені прийоми допомоги, полегшення чи ускладнення завдань за умови неодноразового застосування кожного з них забезпечать практичну основу для реалізації принципу диференційованого підходу в навчанні молодших школярів. Застосовуючи принцип диференційованого підходу, вчитель має бути тактовним, спиратися на позитивні риси характеру дитини. Не слід оперувати словами "сильні учні", "слабкі учні". Краще відзначити ступінь просування дітей в опануванні вмінь, а також самостійність, оригінальність розв'язку і т. ін. §17. Перевірка й оцінювання знань, умінь і навичок учнів з математики Знання, уміння і навички учнів з математики оцінюють за результатами усного опитування, поточних і підсумкових письмових робіт. Під час перевірки письмових робіт з математики слід розрізняти грубі і негрубі помилки. До грубих помилок належать: • обчислювальні помилки в прикладах і задачах; • помилки у визначенні порядку виконання арифметичних дій: Методика викладання математики в початкових класах 93 • неправильне розв'язування задачі (пропуск дій (дії)), неправильний добір дій (дії), зайві дії; • незакінчене розв'язання задачі чи прикладу; • невиконане завдання (учень не приступив до його виконання). Негрубими помилками є: • нераціональні прийоми обчислення, якщо ставилась вимога скористатися такими прийомами; • неправильна побудова чи постановка запитання до дій (дії) під час розв'язування задачі; • неправильне чи неграмотне з точки зору стилістики або за змістом формулювання відповіді задачі; • неправильне списування даних (чисел, знаків) задачі з правильним її розв'язанням; • не доведене до логічного кінця (незакінчене) перетворення. Дві негрубі помилки вважають за одну помилку. Знання, уміння і навички учнів з математики перевіряються в усній та письмовій формах. Спільними наказами Міністерства освіти і науки України та Академії педагогічних наук України від 04.09.2002 р. № 428/48 впроваджено 12-бальну шкалу оцінювання навчальних досягнень учнів у системи загальної середньої освіти, а наказом від 12.07.2002 р. затверджено критерії оцінювання навчальних досягнень учнів початкових класів. Ці критерії опубліковано в "Інформаційному збірнику Міністерства освіти і науки України", а також у журналі "Початкова школа" (2002 р., № 8). Оцінювання навчальних досягнень учнів 1—2 класів здійснюється пербально, 3—4 класів — за 12-бальною шкалою. За рішенням педагогічної ради загальноосвітнього навчального закладу навчальні досягнення учнів 2 класів можуть оцінюватися в балах. Впровадження нової системи контролю та критеріїв оцінювання ідійснюється з метою гуманізації та демократизації навчально-виховного процесу, реалізації завдань особистісно орієнтованого навчання. Визначення ріння навчальних досягнень учнів важливе тому, що навчальна діяльність у кінцевому підсумку має дати не тільки суму знань, умінь і навичок, а й сформувати компетентність людини як самоздатність до оптимальних дій. Оцінювання — це процес встановлення рівня навчальних досягнень учня и оволодінні змістом предмета порівняно з вимогами чинних програм. Об’єктивність і точність оцінок забезпечуються критеріями оцінювання. І якими критеріями є: якість знань, рівень сформованості вмінь, рівень оволодіння досвідом творчої діяльності. На основі вказаних критеріїв виділяються чотири інтегрованих рівні досягнень учнів початкових класів: I рівень — початковий — 1 — 3 бали; II рівень — середній — 4 - 6 балів; I11 рівень — достатній — 7 — 9 балів; IV рівень — високий — 10 — 12 балів. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 94 Подамо рекомендації для оцінювання усних відповідей. Високий рівень — учень правильно відповідає на всі запитання, самостійно застосовує на практиці окремі теоретичні положення; без помилок і доволі швидко обчислює, свідомо використовуючи властивості арифметичних дій; самостійно розв'язує задачі й пояснює хід розв'язування; безпомилково називає відомі геометричні фігури, вміє виконати практичне завдання — виміряти чи накреслити; виконує прості вправи, пов'язані з буквеною символікою (читання буквених виразів, знаходження їх значень за даними числовими значеннями букв, розв'язування рівнянь відповідно до програми). Достатній рівень — коли відповідь загалом задовольняє попередні вимоги, але учень допускає окремі неточності у поясненні математичних фактів, прийомів обчислень; не завжди використовує в обчисленнях раціональні прийоми, часом припускається негрубих помилок; працюючи над задачею, не зовсім точно пояснює хід розв'язування чи результати дій; допускає огріхи, виконуючи вимірювання і креслення. Усі ці недоліки школярі легко виправляють за вказівкою вчителя. Середній рівень — якщо учень правильно розв'язує більшість запропонованих прикладів, але не вміє пояснити прийом обчислення; допускає в обчисленнях помилки, які виправляє за допомогою вчителя; хоч і помиляється у розв'язуванні задачі, поясненні, проте за допомогою вчителя виконує завдання. Початковий рівень — учень не засвоїв більшої частини програмового матеріалу, не може впоратися з розв'язуванням задачі та обчисленнями навіть за допомогою класовода. Для зразка за журналом "Початкова школа" подамо норми оцінювання письмових робіт з математики.
Методика викладання математики в початкових класах 95
Підсумкове оцінювання знань, умінь і навичок Підсумкову оцінку за семестр або за рік виставляють на основі спостережень учителя за повсякденною роботою учня, усного опитування, поточних і підсумкових контрольних робіт, яким надається перевага. §18. Особливості уроку математики в 1 класі У першому класі чотирирічної початкової школи тривалість уроку 35 хв. На уроці є 1 — 2 фізкультурні паузи. Домашніх завдань не задають. Учні мають навчитися лічити предмети, називати, читати й записувати числа до 20; засвоїти таблиці додавання і віднімання в межах 10, оволодіти вміннями розв'язувати деякі арифметичні задачі на одну дію та вимірювати довжину відрізків за допомогою сантиметрової лінійки. Одним з важливих виховних завдань курсу математики, особливо його початкового етапу, є формування в дітей умінь і навичок жити і вчитися в колективі. Учень повинен навчитись підпорядковувати свою навчальну роботу правилам шкільного життя, діяти відповідно до вимог учителя. Він має оволодіти уміннями слухати і відповідати на поставлені запитання. Без цього неможлива фронтальна робота в класі. У шестирічних дітей переважають процеси збудження над процесами гальмування. У них нестійка увага, вони швидко втомлюються сидіти в одному положенні, їх організм потребує великої кількості рухів. Точні рухи вимагають від дитини великих зусиль. Тому вправи на оволодіння навичками письма мають бути короткочасними. Треба враховувати, що для шестирічного учня важливо, щоб учитель звертав увагу саме на нього, до нього звернувся із запитанням, його викликав до дошки, його роботу оцінив. Відсутність такої особистої уваги знижує інтерес до занять. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 96 Важливою особливістю психічних процесів учнів шестирічного віку є конкретність сприймання, наочно-образний характер мислення. Вони краще запам'ятовують факти, події, опис зовнішнього вигляду предметів, схильні до механічного заучування. Значну роль у психічному розвитку першокласника відіграє наслідування. Він порівнює свою поведінку чи навчальну діяльність з певним зразком. Найавторитетнішим зразком для нього є вчитель. Учитель навчає дітей правильно поводитись у класі, коридорі, на подвір'ї, для цього він проводить спеціальні вправи на засвоєння норм такої поведінки, опрацьовуючи спочатку окремі операції, а потім і сумарні дії. Учні мають навчитись розміщувати засоби навчання на парті чи на столі, готуватися до уроку, добирати навчальні засоби за вказівками вчителя; відповідати з місця та біля дошки; користуватись дидактичним матеріалом. При цьому вчитель обов'язково мотивує правильну поведінку, з'ясовуючи її перевагу: чому потрібно сидіти саме так, як показано на малюнку; на якій відстані треба тримати зошит чи книжку від очей. Він прагне добитись, щоб правильна поведінка стала потребою учнів. У проведенні уроків з шестирічками зберігає своє значення основний методичний підхід вивчення математики в початкових класах. Вивчення і опрацювання нового матеріалу, закріплення і засвоєння знань здійснюються за допомогою системи вправ. Вправи здебільшого мають предметно-практичний характер. Крім цього, застосовуються пізнавально-дидактичні ігри. Програмний матеріал учні шестирічного віку засвоюють в результаті багаторазового повторення практичних дій. Тому небажано практичні роботи замінювати демонструванням їх. Демонстрація — це початок роботи над засвоєнням якихось знань. Учням потрібно не тільки побачити, як виконуються певні дії, а й самим виконати їх. Для багатьох вправ характерна така послідовність: а) демонстраційне виконання вправи вчителем; б) фронтальна колективна робота — один учень, користуючись демонстраційними наочними посібниками, виконує вправу біля дошки, а решта учнів класу виконує її на індивідуальному набірному полотні; в) самостійна практична робота. Зміст практичних робіт значною мірою визначається підручником. У першому півріччі на практичні вправи і демонстрації відводиться 15—20 хв уроку, на роботу в зошиті — 7—10 хв, а решта часу — на інші види навчальної роботи. Зауважимо, що робота з підручником здебільшого має практичний характер. Розвитку такого вміння потрібно приділяти належну увагу. В роботі з підручником слід виділяти: опрацювання нового матеріалу; самостійну роботу репродуктивного характеру; повторення вивченого матеріалу. Методика опрацювання нового матеріалу загалом визначена системою завдань підручника. Керуючись нею, вчитель ознайомлює дітей з новим матеріалом спочатку шляхом бесіди чи короткого повідомлення. Пояснення вміщує відповідні демонстрації та практичні вправи. Завдання в підручнику в такому разі використовуються для первинного закріплення. Під керівництвом учителя учні розглядають у підручнику малюнки і записи, усно Методика викладання математики в початкових класах 97 відповідають на поставлені запитання, виконують потрібні практичні завдання. При розгляді нового матеріалу, який є аналогічним до попереднього, послідовність дій можна змінювати: спочатку проводиться бесіда за матеріалом підручника, а потім організовуються фронтальна та індивідуальна роботи на основі наочних посібників і практичних вправ. Запитання і вправи репродуктивного характеру, що охоплюють всі питання кожної теми, у поєднанні з бесідою вчителя сприяють активному осмисленню, запам'ятовуванню, закріпленню та узагальненню нового матеріалу. Крім цього, вони дають цілісну картину засвоєння його учнями. У першому класі це вправи на лічбу, написання цифр, порівняння чисел, їх склад, заучування таблиць додавання і віднімання, розв'язування прикладів, побудова відрізків та вимірювання їх довжин. Репродуктивну самостійну роботу з підручником здебільшого організовують за поданим у ньому зразком. Деякі завдання учні виконують під диктовку вчителя. Нерідко роботу здійснюють поетапно, з перевіркою правильності виконання кожної частини завдання. Повторення за підручником вивченого матеріалу проводять у формі фронтальної бесіди, усного або письмового виконання завдання. Робота часто поєднується з демонстраціями на набірному полотні чи записами на дошці. Формування математичних понять на початковому етапі має пов'язуватись з розвитком мовлення дитини. Те, що не проходить через мовний апарат дитини, залишається для неї мало усвідомленим. Згідно з теорією поетапного формування розумових дій, яку розробили відомий психолог П.Я. Гальперін і його послідовники, початковий етап процесу формування розумової дії — це складення попереднього уявлення про завдання. Для цього за зразком формується орієнтовна основа дії, тобто поділяється дія на такі дрібні операції, які посильні для учнів і ґрунтуються на засвоєних ними раніше знаннях, уміннях і навичках. Після ознайомлення з навчальним завданням (коли сформується орієнтовна основа) учні починають безпосередньо виконувати саму дію. Спочатку це має бути дія з матеріальними предметами. Цю вимогу не слід ототожнювати з принципом наочності в навчанні. Йдеться про пошук матеріалізованої форми дії та аналізу її змісту. За теорією поетапного засвоєння розумових дій оволодіння матеріальною чи матеріалізованою дією ще недостатнє для перенесення дії у план уявлень (внутрішню мову). Перенесення здійснюється спочатку проговорюванням вголос. Без цієї навички виконання дії не буде стійким. Пропущення етапу проговорювання призводить до збільшення кількості помилок порівняно з навчанням, що охоплює всі етапи. Дидактична гра як форма організації навчальної діяльності учнів шестирічного віку не є домінуючим видом завдань. Значно ширше застосовуються ігрові ситуації, зокрема персонажі казок, мультфільмів, дитячих оповідань (Незнайко, Буратіно, Чебуращка) для постановки запитань і завдань. Проте для учнів будь-яка ігрова форма завдання є грою. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 98 На уроці гра організовується не для того, щоб діти погрались, а щоб чогось навчились. Тому після проведення гри варто час від часу запитувати: "Чого ви навчилися в цій грі?". Слід оцінювати знання учнів, здобуті в процесі гри. Гра не передує виконанню навчальних завдань і не чергується з ними, а є однією з форм організації колективної роботи учнів у класі. В іграх ставляться конкретні математичні завдання. Гра на початку уроку має збудити думку дитини, допомогти їй зосередитися. Якщо ж учні стомлені, то варто провести з ними рухливу гру. В усіх випадках процес гри не має відвертати увагу дітей від математичної мети її проведення. Бажано також застосовувати гру не тільки з близькою, а й з віддаленою метою, наприклад, для формування загальнонавчальних умінь. У грі мають брати участь (в тих чи інших ролях) усі учні, тому до її проведення слід готувати дітей завчасно. Отже, бажано, щоб гра чи ігрова ситуація мала багаторазове застосування. Інструкція проведення гри має бути чіткою й зрозумілою, сам процес гри необхідно контролювати й оцінювати. Не можна принижувати гідність учня за поразку в грі. Не слід поділяти учнів на сильних і слабких, встигаючих і невстигаючих. Для проведення гри потрібно мати достатню кількість ігрового матеріалу, а також набірне полотно, фланелограф, магнітну дошку. Ігровий матеріал має бути чітко систематизований для зручності користування. Розгляньмо методику використання іграшок для лічби, створення ігрових ситуацій та проведення власне математичних ігор. У першому класі іграшкові предмети використовуються переважно для лічби, у деяких випадках — також для формування математичних понять. Лічба предметів для дітей є цікавою, якщо вона потребує спостережливості, порівняння, виділення предметів з їх сукупності. Ігри, не пов'язані з лічбою предметів, проводять під назвами: "Скільки?", "Жива нумерація", "Зроби так", "Продовж лічбу", "Яке число пропущено?", "Який за порядком?", "Більше, менше, стільки ж" тощо. У вивченні першого десятка потрібно, щоб лічба і дії над числами не тільки спиралися на дії з предметами. Не менш важливо, щоб учні збагачувалися у математичному відношенні. Коли шестирічки роблять перші кроки у навчанні, перехід від оперування предметами до роботи з числами, а потім до дій з числами є обов'язковим. У процесі лічби такий перехід можна здійснювати на основі вимоги: "Полічити трикутники і покласти стільки ж кружечків". Біля дошки варто застосувати ситуацію ускладнення. Кружечків треба поставити стільки, скільки й паличок. Проте кружечки такі великі, що їх не можна поставити в парі з паличками. Ряд кружечків буде довгим. Величина і колір іграшок не мають затіняти математичну мету їх використання. Поступово у 1 класі треба перейти до використання силуетних картинок тварин, овочів, фруктів, машин, інструментів тощо. Частину таких силуетних картинок бажано мати і для індивідуальної роботи. Методика викладання математики в початкових класах 99 Застосовувати ігрові ситуації доцільно під час розв'язування прикладів і задач. З досвіду роботи відомо, що основним видом (будемо називати його першим видом) ігрової ситуації у першому класі є використання персонажів казок, мультфільмів, оповідань. Постановка звичайних навчальних запитань і завдань з участю Незнайки, Буратіно збуджує інтерес і підтримує активну діяльність кожної дитини протягом тривалого часу (3 — 5 хв). Прийоми залучення знайомих дітям персонажів елементарно прості. Здебільшого використовується лялька для зображення дійової особи. її слова промовляє учитель. Суть ігрової ситуації з'ясовується у вступній частині: "Незнайці треба знайти помилку"; "Буратіно треба виручити з біди"; "Чебурашці треба допомогти розв'язати задачу". Далі йде формулювання завдання. Значна частина завдань використовується з підручника. Варіаціями ігрової ситуації є читання листа від Буратіно, слухання прохання Незнайки, що звучить по телефону чи записане на магнітофонну плівку. Другим видом ігрових ситуацій є використання у сюжеті задач дій тварин. Наприклад: "На галявині гралися 3 зайченят. До них прибігли ще 2 зайчики. Скільки зайченят стало на галявині?". Такі сюжети використовують не тільки для розв'язування задачі, а й для її складання. До третього виду ігрових ситуацій належать так звані лічилки або цікаві ішрави. Це віршовані завдання. Зрозуміло, що заучувати їх напам'ять учням ІЦ' СЛІД. До четвертого виду ігрових ситуацій належать ігри-змагання. Здебільшого ні- парні або групові змагання у розв'язуванні двох стовпчиків прикладів та V називанні таблиць арифметичних дій. Варіанти ігор бувають такі: а) хто більше і правильно розв'яже і запише відповідей до прикладів за 1 хв.; б) хто швидше запише всі випадки складу чисел з двох доданків; в) хто більше назве прикладів із заданими результатами; г) хто безпомилково і чітко розкаже (запише) таблицю додавання числа 3; г) яка команда безпомилково назве таблицю віднімання числа 3. В оцінюванні переможців треба знати міру. Не варто їх дуже хвалити. Обов'язково слід знайти щось хороше і в "переможених" (усі вміють розв’язувати такі приклади). До п'ятого виду ігрових ситуацій належать завдання ущільненого характеру. Цей вид добре ілюструють такі ігри: "Доповнити до числа 5", Магазин", "Риболов" тощо. До шостого виду ігрових ситуацій належать власне математичні ігри. У першому класі це: "Кругові приклади", "Лото", "Доміно". Усі вони на додавання і віднімання чисел в межах 10. "Кругові приклади" розв'язують одночасно всі учні, причому самостійно. Гра в лото проводиться на основі індивідуальних карток або на основі натурального ряду чисел від 1 до 10. останньому випадку вчитель диктує приклад, а учень у натуральному ряді закриває фішкою (кружечком) те число, яке є відповіддю до цього прикладу. Якщо відповідь повторюється, то учень кладе на число дві фішки. "Доміно" Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 100 у 1 класі використовується як парна гра, тому для її проведення потрібно мати відповідну кількість наборів такої гри. У практичній роботі використовуються казки, проводяться ігри на відгадування, розпізнавання фігур чи їх зміну, кмітливість (яка спирається на кількісну характеристику) та ін. Ігрових ситуацій можна створити багато, але всі вони мають підпорядкуватись головній меті: учень повинен працювати над математичними завданнями. На ознайомлення з кожним новим числом здебільшого відводиться два уроки. На кожному з них діти вчаться писати нову цифру і закріплюють навички написання раніше розглянутих цифр. Отже, писати цифри школярі вчитимуться протягом усього часу вивчення нумерації чисел першого десятка, а закріплювати навички письма — протягом всього часу навчання у 1 класі. Тому на перших уроках ознайомлення учнів з написанням цифр не слід їх перевантажувати такими вправами. У дітей ще не розвинені дрібні м'язи, і вони швидко втомлюються. Готуючись до написання цифр, учні виконують деякі спеціальні вправи у зошиті з друкованою основою. Крім цих вправ, радимо ще практикувати заштриховування (не зафарбовування) тих чи інших фігур (малюнків) олівцем або кульковою ручкою. Штрихувати треба у різних напрямках. Ознайомлення з новою цифрою проводиться так: а) учитель записує на дошці друковану і письмову форми цифри, аналізує і порівнює ці форми (розповідає, з яких елементів складається цифра); б) пояснює хід руху руки при написанні цифри і розміщення елементів цифри у клітинці аркуша; в) діти виконують "написання" цифри у повітрі або на парті; г) учні пишуть цифру на окремих (пробних) аркушах паперу в клітинку; ґ) два-три учні пишуть цифру на дошці, а вчитель та інші діти аналізують це написання; д) цифру пишуть у зошитах з друкованою основою. Написання цифри у звичайних учнівських зошитах практикується пізніше. Під час письма вчитель ходить між партами, допомагає правильно писати, виправляє помилки. Написання цифр треба поєднувати з читанням відповідних чисел. У першому класі кожну цифру діти пишуть на одну клітинку. Практикують написання цифр через одну клітинку. Охайне й правильне написання цифр — важлива умова розвитку культури математичного письма. Однією з особливостей навчання учнів шестирічного віку розв'язувати задачі є застосування пропедевтичного етапу роботи — розв'язування задач без арифметичних дій. Відповіді учні знаходять перелічуванням предметів та їх малюнків. Особливості пропедевтичного стану є такими: не ставиться завдання розчленувати задачу на умову і запитання; умову задачі вчитель здебільшого повідомляє у ході виконання практичних дій чи відповідних малюнків. Запитання задачі ставиться вже на основі виконаних дій з предметами чи за кінцевим малюнком. Подамо два зразки такої роботи. Методика викладання математики в початкових класах 101 Задача 1. На годівниці спочатку було 3 горобці. Потім прилетіло 2 синиці. Скільки всього птахів стало на годівниці? Прочитавши задачу, учитель організовує практичну роботу дітей. Хід бесіди. Відповідь знайдемо за допомогою кружечків. На годівниці було 3 горобці. Покладіть на парті 3 сірих кружечки. Далі сказано, що прилетіло ще 2 синички. Покладіть у цей рядок ще 2 жовтих кружечки. Що означає кожний сірий кружечок? Кожний жовтий кружечок? Покажіть усіх горобців, усіх синичок, усіх птахів. Нам треба знайти, скільки всіх птахів стало на годівниці. Полічіть кружечки і дайте відповідь на запитання. Надалі задачі на знаходження суми на пропедевтичному етапі будуть розв'язуватись як на основі предметних дій, так і за малюнками, які діти виконують у зошитах і на дошці. Задача 2. У бочці було 8 відер води. Для поливання дерев витратили 5 відер. Скільки відер води залишилося в бочці? Хід бесіди. У бочці було 8 відер води. Візьміть олівець і намалюйте в зошиті в одному рядку 8 кружечків. Що означає кожний кружечок? (Одне відро води). 5 відер води витратили для поливання дерев. Візьміть олівець і перекресліть 5 кружечків. Що означає кожен перекреслений кружечок? (Відро води, використане для поливання дерев). Покажіть решту кружечків. Скільки залишилось незакреслених кружечків? На пропедевтичному етапі діти мають справу із задачами-діями. Оперуючи предметними множинами, вони усвідомлюють, що операції об'єднання нідповідає дія додавання, а операції вилучення частини предметів — дія піднімання. Надалі (на основному етапі) учні розв'язують задачі із застосуванням арифметичних дій. Предметна наочність, інсценування сюжету задачі нідіграють велику роль і на цьому етапі. Однак застосовується така предметна ситуація, що виключає знаходження відповіді перелічуванням предметів. Обов'язково треба спочатку вибрати дію, а потім її виконати. Для розвитку пміння вибирати дію для розв'язання задачі застосовують різноманітні прийоми. Опрацювання геометричного матеріалу. За допомогою лінійки учням важче проводити вертикальну пряму, ніж горизонтальну, вони намагаються повертати зошит чи аркуш. Це треба враховувати і поступово відучувати їх під цього, показуючи правильне положення лінійки, олівця і рук під час креслення відрізків. Шестирічні діти креслять відрізки за допомогою лінійки із зупинками. Треба навчити їх креслити неперервно, відразу від початку і до кінця. Пояснюючи будову лінійки, спочатку показують початок відліку (штрих і позначкою 0), потім перший сантиметр, другий сантиметр; після цього шпначають на лінійці 3 см, 5 см. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 102 Геометричні відомості учні засвоюють у процесі безпосередніх спостережень геометричних фігур та їх елементів, виготовлення моделей цих фігур, під час виконання практичних, графічних і вимірювальних робіт. Особливу увагу вчитель приділяє розвитку просторових уявлень першокласників. Розглянемо по одному уроку з двох основних тем програми першого класу: "Нумерація чисел першого десятка" та "Додавання і віднімання в межах 10". Тема "Число і цифра 4. Написання цифр. Порівняння чисел у межах 4". І. Повторення та закріплення вивченого. 1. Гра "Не помились". Учитель показує картки з малюнками предметів, а учні піднімають картки з відповідними цифрами. Учитель показує цифри, а учні відкладають відповідну кількість паличок. 2. Називання чисел 1, 2 і 3 у порядку від меншого до більшого і від більшого до меншого. II. Вивчення нового матеріалу.
 Мал. 30 Полічіть єнотів на малюнку (мал. 30). Розгляньте друковану цифру 4. 2. Утворення числа 4. — Розглянемо, як можна утворити число 4. Покладіть 3 кружечки, а під ними — З трикутники. Якому числу відповідає кожна з цих груп? (Числу 3). Скільки предметів буде в кожній групі, якщо до кружечків додамо 1 кружечок, а до трикутників — 1 Трикутник? Як утворили 4 кружечки? 4 трикутники? Отже, щоб стало 4 предмети, необхідно до 3 додати 1. 3. Бесіда за вправою 1. Мал. 31 Скільки намистинок на нитці зліва? Скільки справа? Як утворили число 4? (Мал. Зі). 4. Порівняння чисел у межах 4 за вправою 2. Полічи в кожній групі жовті й зелені кружечки. Здобуті числа порівняй (мал. 32). Методика викладання математики в початкових класах 101 Мал. 32 5. Показ і пояснення вчителем написання цифри 4. Написання рядка цифри 4. III. Розвиток знань учнів. 1. Читання чисел 1, 2, 3, 4 від меншого до більшого і від більшого до меншого. 2. Лічба і порівняння кількості кружечків за малюнками (вправа 3). (Результати порівняння необхідно записати). Полічи, скільки кружечків у стовпчиках. Порівняй числа кожної пари (мал. 33). О оо оо о оо оо оо оо о оо оо оо оо оо 3>2 Мал. 33 3. Лічба і порівняння кількості вишень за малюнками (вправа 4) (мал. 34). 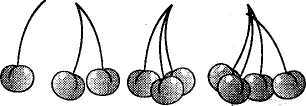 Мал. 34 4. Написання цифр 2 і 4. IV. Підсумок. .-------- Розповісти, що треба зробити, щоб одержати число 4, якщо маємо число 3. Тема "Складання таблиць додавання і віднімання числа 2. Розв'язування прикладів виду 7 + 2— 1,8 — 2-2. Віднімання за допомогою числового відрізка, і кладання і розв'язування задач". І. Фронтальне опитування. 1. 1) Розкажіть таблицю додавання числа 1. 2) Розкажіть таблицю віднімання числа 1. 3) 3 прикладу 2 + 8 = 10 складіть приклад на віднімання числа 2. 4) Повідомте нідповіді до прикладів: 3+1 + 1; 9-1-1; 7— 1 — 1. 2. Гра "Яких чисел не вистачає?". Клас ділиться на дві команди. Учитель називає два числа, а учні кожної команди почергово називають числа, що стоять між вказаними. Перемагає команда, гравці икої дііли більше правильних відповідей. II. Вивчення нового матеріалу. І. Робота над складанням таблиць додавання і віднімання числа 2. Розділ IV. Складові частини уроку математики. Методи вивчення нового матеріалу 104  Мал. 35 За малюнками клітинок поясни, як знайшли відповіді до прикладів (мал. 35). Прочитай таблиці додавання і віднімання числа 2. 2. На дошці записано таблиці додавання і віднімання числа 2 без результатів (без відповідей). За вказівкою вчителя учні вибірково повідомляють відповіді до окремих прикладів. 3. Застосування таблиць під час розв'язування прикладів на дві дії. Використовуючи таблиці додавання і віднімання числа 2, розв'яжи приклади (вправа 2). 6+1+2 7-2+1 7+1-2 4. Бесіда про розв'язування прикладу 8 — 2 за малюнком числового відрізка (вправа 3) (мал. 36). 0 12 3 4 5 6 7 -2=П 012345678 9 III. Складання і розв'язування задач за малюнками. 1. Фронтальна робота за вправою 4 (малюнок зліва). 2. Самостійна робота за вправою 4 (малюнок справа). Вправа 3. Склади і розв'яжи задачі на вказані дії (мал. 37). 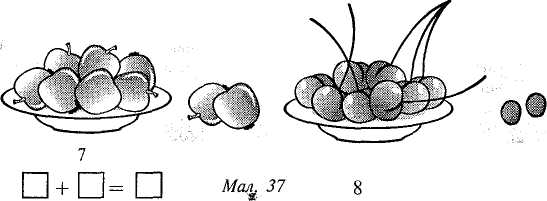 Методика викладання математики в початкових класах 105 Після розв'язування і запису розв'язання учні повідомляюсь умову і запитання задачі, читають приклад і відповідь. : IV. Розвиток знань учнів. 1. Повідомлення таблиці віднімання числа 1. 2. Виконання завдань на визначення складу числа 8. V. Підсумок. Складали таблиці додавання і віднімання числа 2. В обох зразках уроків головну увагу приділено поясненню нового матеріалу. Тому значну частину часу займає бесіда вчителя, але вона вміщує не тільки відповіді учнів, а й практичне виконання операцій, дії з предметами. Учитель пояснює новий матеріал на основі малюнків і записів у підручнику. РОЗДІЛ V НУМЕРАЦІЯ ЧИСЕЛ І ДОДАВАННЯ ТА ВІДНІМАННЯ В МЕЖАХ 10 У вивченні математики в першому класі певну роль відіграє дочисловий період, матеріал якого опрацьовується у вигляді окремих уроків. Програмовий матеріал дочислового періоду охоплює такі питання: властивості й відношення предметів, взаємне їх розміщення, практичні вправи з групами предметів. Опрацьовуючи ці теми, вчитель має сформувати в дітей уявлення про колір, розміри, матеріал, з якого виготовлені предмети; розміщення їх на площині і в просторі, відношення за довжиною, висотою, шириною тощо, порівняння сукупностей предметів; уявлення про геометричні фігури — круг, трикутник, чотирикутник. Упродовж розгляду цього матеріалу учні повинні вчитися лічити в межах 10. Розгляньмо один з перших уроків. Тема "Порядкова лічба. Поняття зліва — направо, справа — наліво; один, усі, кожний, решта; вищий — нижчий. Підготовка до написання цифр". І. Повторення і закріплення вивченого. 1. Порівняння паличок за довжиною. На набірному полотні 3 довгі і 5 коротких паличок. Полічіть окремо довгі й короткі палички. Скільки довгих паличок? Скільки коротких? 2. Порівняння предметів за довжиною. За вказівкою вчителя учні порівнюють довжину палички й олівця, олівця і ручки, кілька пар предметів з інтер'єру класної кімнати. II. Вивчення нового матеріалу. 1. Порядкова лічба. 1) Учитель викликає до дошки чотирьох учнів, пропонує їм стати один за одним так, ніби вони виходять з класу, і запитує: "Хто стоїть першим у цьому ряді? Хто другим?" і т. д. Учитель показує зразок порядкової лічби і пропонує дітям повернутися так, ніби вони заходять до класу. Знову повторює ті самі запитання. Далі на проханий вчителя учні повертаються обличчям до класу. Вчитель звертає їхню увагу на те, що тепер відповідь на запитання "Хто стоїть першим?" потребує додаткових пояснені, про напрям лічби. 2) Бесіда за завданням підручника (мал. 38).  Мал. 38 Методика викладання математики в початкових класах 107 Полічи кружечки зліва направо. На якому місці зелений кружечок? Полічи окремо трикутники і чотирикутники; трикутники і чотирикутники разом. 3) Лічба предметів з використанням понять "один", "усі", "решта", "кожний" (да завданням підручника) (мал. 39).  Мал. 39 Назви якусь одну пташку. Назви решту пташок. Полічи птахів зліва направо. На якому місці ластівка? Полічи птахів справа наліво. На якому місці ластівка? Варто поставити ще такі завдання: "Назви кожну пташку. Полічи всіх пташок". 2. Порівняння предметів за висотою (мал. 40).  Мал. 40 Спочатку учні порівнюють за висотою предмети інтер'єру, а потім виконують інпдання за малюнком підручника. Скільки всього звірят? Назви звірят від найнижчого до найвищого. Між якими шірятами мишеня? III. Написання паличок. Пояснення руху руки під час написання паличок. Написання рядка паличок у іоіниті за зразком у підручнику. IV. Підсумок. Лічили предмети за порядком. Лічили справа наліво, зліва направо. Порівнювали предмети за висотою. Писали палички. Під час проведення перших уроків математики для підтримання інтересу I працездатності учнів важливо своєчасно змінювати види їхньої діяльності II урізноманітнювати завдання. Так, виділення за певною властивістю окремих предметів або їх груп треба пов'язувати з термінами "будь-який", "кожний", "один", "всі". Дітей треба вчити одночасно називати й пока-іуиати кожний предмет, будь-який предмет, усі предмети. Відповідні вміння формуються на основі багаторазового виконання дій: показування, називання II розфарбовування предметів. Розділ V. Нумерація чисел і додавання та віднімання в межах 10 108 У плані підготовки до вивчення теми "Лічба предметів" під час ознайомлення з правилами лічби доцільно навчити дітей показувати предмети, починаючи з будь-якого, називати й показувати всі предмети, не пропускати жодного і не називати один предмет двічі. Тому перед виконанням таких завдань щоразу слід запитувати: "З якого предмета почнемо показувати?". У дочисловий період особливу увагу треба приділяти питанням розвитку та формування в дітей загальних навчальних умінь і навичок. |
