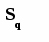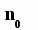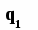Мат_методи дослідження операційі. Навчальний посібник Київ 2008 Зміст Анотація 3 План курсу 4 Лекція Вступ. Цілі, критерії, обмеження. 4

• Название: Навчальний посібник Київ 2008 Зміст Анотація 3 План курсу 4 Лекція Вступ. Цілі, критерії, обмеження. 4
• Анкор: Мат_методи дослідження операційі.doc
• Дата: 01.09.2018
• Размер: 0.81 Mb.
• Имя файла: Мат_методи дослідження операційі.doc
• Тип: Навчальний посібник; #23907
• страница: 11 из 13

Число оптимальних партій k₀ за час θ з урахуванням (7.5), (7.9) і (7.3) дорівнює

k0 =	N	=		с2 N θ	= θ		с2 b
	n0			2с1			2с1

Час витрати оптимальної партії на підставі (7.4) з урахуванням (7.9) і (7.3) дорівнює

T0 =	n0	= n0	θ		(7.14)
	b		N

	T0 =		2с1 θ	=		2с1	(7.15)
			с2 N			с2 b

Приклад. Потреба складального підприємства в деталях деякого типу складає 120 000 деталей на рік, причому ці деталі витрачаються в процесі виробництва рівномірно і безупинно. Деталі замовляються раз на рік і постачаються партіями однакового обсягу, зазначеного в замовленні. Збереження деталі на складі коштує 0,35 гр.о. на добу, а постачання партії – 10 000 гр.о. Простоювання виробництва через відсутність деталей неприпустимо.

Визначити найбільш економічний обсяг партії й інтервал між постачаннями, які потрібно вказати в замовленні (вважається, що постачальник не допускає затримок постачань).

Рішення. За умовою витрати на одну партію складають с₁ = 10 000 гр.о., витрати на збереження одиниці запасу в добу с₂ = 0,35 гр.о. Загальний проміжок часу θ = 1 рік = 365 днів, а загальний обсяг запасу за цей період складає N = 120 000 деталей.

По формулі (7.9) визначається n₀ ≈ 4335 деталей, а по формулі (7.14) T₀ =13,2 ≈ 13 днів.

Відповідь. Найбільш економічний обсяг партії n₀ ≈ 4335 деталей.

Оптимальний інтервал часу між постачаннями T₀ ≈ 13 днів.

Однопродуктова статична детермінована модель без дефіциту з «розривами» цін.

У розглянутій задачі не враховуються питомі витрати на придбання товарів, тому що вони постійні і не впливають не рівень запасу. Однак часто ціна одиниці товару залежить від розміру закуповуваної партії. У таких випадках ціни міняються стрибкоподібно, наприклад, при наданні оптових знижок. При цьому в моделі керування запасами необхідно враховувати витрати на придбання товарних запасів.

Розглянемо однопродуктову статичну детерміновану модель без дефіциту, у якій ціна одиниці товару дорівнює ц₁ при n < q і дорівнює ц₂ при n ≥ q, причому ц₁ > ц₂ і q – розмір замовлення, при перевищенні якого надається знижка.

Сумарні витрати в одиницю часу при n < q з урахуванням (7.8) і (7.3) рівні:

S1(n) = b ц1 + b	с1	+ n	с2		(7.16)
	n		2

Сумарні витрати в одиницю часу при n ≥ q з урахуванням (7.8) і (7.3) рівні:

Sq(n) = b ц2 + b	с1	+ n	с2		(7.17)
	n		2

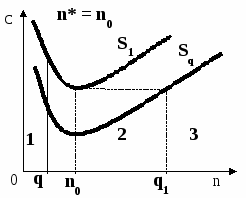
Мінімум функцій S₁(n) і S_q(n), відповідно до формули Уилсона, досягається в точці n₀ (7.10). З аналізу графіків функцій S₁(n) і S_q(n) (мал. 7.3) випливає, що оптимальний обсяг замовлення n* залежить від того, в якому місці відносно трьох показаних на мал.7.3 зон знаходиться точка розриву ціни q. Розташування зон визначається шляхом визначення невідомого q₁ (при відомому з (7.10) n₀) з рівняння S₁(n₀) = S_q(q₁).

Тоді зони розподіляються в такий спосіб:

Зона 1: 0 ≤ q < n₀;

Зона 2: n₀ ≤ q < q₁;

Зона 3: q ≥ q₁.

У 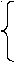залежності від розташування крапки розриву ціни q, оптимальний розмір замовлення визначається в такий спосіб:

n* =		n0, якщо 0 ≤ q < n0 (зона 1)
		q, якщо n0 ≤ q < q1 (зона 2)	(18)
		n0, якщо q ≥ q1 (зона 3)
Мал. 7.3.

Алгоритм визначення n* можна подати в такому вигляді.

1. 
   Визначити n₀. Якщо q < n₀ (зона 1), то рішення n* = n₀ отримане й алгоритм завершується. В іншому випадку переходимо до кроку 2.
   
2. 
   Визначити q₁ з рівності S₁(n₀) = S_q(q₁) і установити, де відносно зон 2 і 3 знаходиться значення q:
   

а) якщо n₀ ≤ q < q₁ (зона 2), то n* = q;

б) якщо q ≥ q₁ (зона 3), то n* = n₀.
Тема 8.