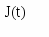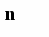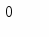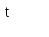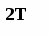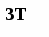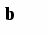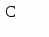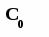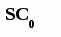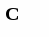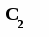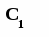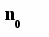Мат_методи дослідження операційі. Навчальний посібник Київ 2008 Зміст Анотація 3 План курсу 4 Лекція Вступ. Цілі, критерії, обмеження. 4
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Лекція 10. Управління запасами.Правильне і своєчасне визначення оптимальної стратегії керування запасами, а також нормативного рівня запасів дозволяє звільнити значні оборотні кошти, заморожені у вигляді запасів, що, у кінцевому рахунку, підвищує ефективність використовуваних ресурсів. Визначення1. Керування запасами складається у знаходженні такої стратегії поповнення і витрати запасів, при якій функція витрат на обслуговування запасів приймає мінімальне значення. Моделі керування запасами характеризуються такими параметрами. Попит. Потреба в запасі. Попит на продукт, що запасається, може бути детермінованим (у найпростішому випадку - постійним у часі) чи випадковим. Випадковість попиту описується або випадковим моментом попиту, або випадковим обсягом попиту в детерміновані або випадкові моменти часу. Поповнення складу. Поповнення складу може здійснюватися або періодично через визначені проміжки часу, або в міру вичерпання запасів, тобто зниження їх до деякого рівня. Обсяг замовлення. При періодичному поповненні і випадковому вичерпанні запасів обсяг замовлення може залежати від того стану, що спостерігається в момент подачі замовлення. Замовлення звичайно подається на одну й ту саму величину при досягненні запасом заданого рівня – так званої точки замовлення. Час доставки. В ідеалізованих моделях керування запасами передбачається, що замовлене поповнення доставляється на склад миттєво. В інших моделях розглядається затримка постачань на фіксований чи випадковий інтервал часу. Вартість постачання. Як правило, передбачається, що вартість кожного постачання складається з двох компонентів – разових витрат, що не залежать від обсягу партії, що замовляється, і витрат, що залежать від обсягу партії. Витрати збереження. У більшості моделей керування запасами вважають обсяг складу практично необмеженим, а контролюючою величиною служить обсяг запасів, що зберігаються. При цьому вважають, що за збереження кожної одиниці запасу в одиницю часу стягується визначена плата. Штраф за дефіцит. Будь-який склад створюється для того, щоб запобігти дефіциту певного типу виробів у системі, що обслуговується. Відсутність запасу в потрібний момент приводить до збитків, пов'язаним із простоєм устаткування, неритмічністю виробництва і т.д. Ці збитки називаються штрафом за дефіцит. Номенклатура запасу. У найпростіших випадках передбачається, що на складі зберігається запас однотипних чи виробів однорідного продукту. У більш складних випадках розглядається номенклатурний запас. Структура складської системи. Найбільше повно розроблені математичні моделі одиночного складу. Однак на практиці зустрічаються і більш складні структури: ієрархічні системи складів з різними періодами поповнення і часом доставки замовлень, з можливістю обміну запасами між складами одного рівня ієрархії і т.ін. Як критерій ефективності прийнятої стратегії керування запасами виступає функція витрат, що являє собою сумарні витрати на збереження і постачання продукту, що запасається, і витрати на штрафи. Введемо в розгляд функції: А(t) – функцію поповнення запасів; B(t) – функцію витрати запасів; R(t) – функцію попиту на продукт, що запасається, за проміжок часу [0, t]. У моделях керування запасами використовуються похідні цих функцій за часом: a(t) – інтенсивність поповнення запасів; b(t) – інтенсивність витрати запасів; r(t) – інтенсивність попиту запасів. У залежності від властивостей функцій інтенсивностей a(t), b(t), r(t) моделі керування запасами класифікуються в такий спосіб. Якщо функції інтенсивностей не є випадковими, то модель керування запасами називається детермінованою. Якщо, хоча б одна їх їх носить випадковий характер – модель керування запасами називається стохастичною. Якщо всі параметри моделі не міняються в часі, вона називається статичною, в іншому випадку – динамічною. Крім того, моделі керування запасами можуть допускати дефіцит запасів або бути бездефіцитними. Рівень запасу в момент t визначається основним рівнянням запасів J(t) = J0 + A(t) - B(t), (7.1) де J0 - початковий запас у момент часу t = 0. Рівняння (7.1) в інтегральній формі має вид: t t J(t) = J0 + ∫ a(t) dt - ∫ b(t) dt. (7.2) 00 Однопродуктова статична детермінована модель без дефіциту. Припущення про те, що дефіцит не допускається, означає повне задоволення попиту на продукт, що запасається, тобто функції b(t) і r(t) збігаються. Розглянемо деякий інтервал часу θ (наприклад рік). Загальне споживання запасів за який складає N. У найпростішому випадку передбачається, що витрата запасу відбувається безупинно з постійною інтенсивністю, тобто b(t)= b. Ця інтенсивність визначається відношенням загального споживання продукту до часу, протягом якого він витрачається:
Поповнення запасу відбувається партіями однакового обсягу n через однакові відрізки часу Т. Оскільки інтенсивність витрати дорівнює b, то кожна партія буде використана за час Т
Таким чином функція a(t) не є безперервною:
Іншими словами функція інтенсивності постачання a(t) є імпульсною, тобто запас поповнюється миттєво в моменти часу кратні T. Якщо відлік часу почати з моменту надходження першої партії, то рівень запасу в початковий момент часу дорівнює обсягу цієї партії n, тобто J(0) = n. На часовому інтервалі [0, T] рівень запасу зменшується по прямої J(t) = n - bt від значення n до 0. Оскільки дефіцит не допускається, то в момент часу T рівень запасу миттєво поповнюється до колишнього значення n за рахунок надходження партії запасу. Процес зміни J(t) повторюється на кожному часовому інтервалі тривалістю T. Графічно залежність рівня запасу від часу ілюструється мал. 7.1.
Таким чином, задача керування запасами полягає у визначенні такого обсягу партії n, при якому сумарні витрати на створення і збереження запасу були б мінімальними. Позначимо через С сумарні витрати, витрати на створення запасу – через С1, витрати на збереження запасу – через С2, витрати на доставку однієї партії продукту, що не залежать від обсягу партії - с1, витрати на збереження однієї одиниці продукту в одиницю часу – с2. Оскільки за час θ необхідно запастися N одиницями продукту, що доставляється партіями обсягу n, то число таких партій k дорівнює:
Отже С1 = с1k = с1N/n (7.6) Миттєві витрати на збереження запасу в момент часу t рівні с2 J(t). Тоді витрати на збереження за проміжок [0, T] складуть Т T с2 ∫ J(t) dt = с2 ∫ (n-bt) dt 00 або з урахуванням (7.4)
Середній запас за проміжок [0, T] дорівнює nТ/2, тобто витрати на збереження всього запасу при лінійному часі його витрати дорівнюють витратам на збереження середнього запасу. З урахуванням (7.5) одержуємо:
Відзначимо, що витрати С1 обернено пропорційні, а витрати С2 прямо пропорційні обсягу партії n. З огляду на, що З = З1 + З2 сумарні витрати визначаються функцією витрат:
Графіки залежностей С , С1, С2 зображені на мал. 7.2.
В точці минимума функції С(n) її похідна дорівнює 0:
Тоді
або, з урахуванням (7.3)
Формула (7.10) називається формулою Уїлсона чи формулою найбільш економічного обсягу партії. Зауважимо, що добуток С1С2 = 0,5с1с2θN є величина постійна. Як відомо сума двох співмножників приймає найменше значення, коли вони рівні між собою, тобто С1= С2 або
Рівність (7.11) легко перетворити до виду (7.9). З (7.11) випливає, що мінімум загальних витрат задачі керування запасами досягається тоді, коли витрати на створення запасу дорівнюють витратам на збереження запасу. При цьому мінімальні сумарні витрати складають
звідки з урахуванням (7.5) и (7.9), отримуєм С0 = √2с1с2θN або
|