Мат_методи дослідження операційі. Навчальний посібник Київ 2008 Зміст Анотація 3 План курсу 4 Лекція Вступ. Цілі, критерії, обмеження. 4
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Лекція 6. Динамічне програмування.Розподілення капіталовкладень.Динамічне програмування (ДП) – метод оптимізації, пристосований до операцій, у яких процес прийняття рішення може бути розбитий на етапи (кроки). Такі операції називаються багатокроковими. Моделі лінійного програмування, розглянуті раніше, використовуються для прийняття великомасштабних (макроекономічних) рішень. У великих економічних системах постійно потрібно приймати локальні (мікроекономічні) рішення. Моделі ДП цінні тим, що дозволяють на основі стандартного підходу при мінімальному втручанні людини приймати такі рішення. У тому випадку, якщо кожне окреме рішення не оцінюється як істотне, то в сукупності ці рішення можуть вплинути на підсумковий прибуток. Моделі ДП застосовуються при рішенні таких задач:
У загальному вигляді задачу ДП можна сформулювати в такому вигляді. Розглядається керований процес. У результаті керування система (об'єкт керування) S переводиться з початкового стану s0 у стан s’. Припустимо, що керування можна розбити на n кроків, тобто рішення приймається послідовно на кожному кроці, а керування, що переводить систему S з початкового стану в кінцевий являє собою сукупність n покрокових управлінь. Позначимо через Хk керування на k-ому кроці (k=1, 2, ... n). Змінні Хk задовольняють деяким обмеженням, тобто є припустимими. Нехай Х(Х1, Х2, … Хn) – керування, що переводить систему S зі стану s0 у стан s’. Позначимо через sk стан системи після k-го кроку керування. Одержимо послідовність станів s0, s1, … sk-1, sk, …, sn-1, sn = s’... Показник ефективності розглянутої керованої операції – цільова функція – залежить від початкового стану і керування: Z = F(s0, X). Задача покрокової оптимізації (задача ДП) формулюється так: визначити таке припустиме керування Х, що переводить систему S зі стану s0 у стан s’, при якому цільова функція приймає найбільше (найменше) значення. Модель ДП. має такі особливості:
Замість загальної постановки задачі ДП із фіксованим числом кроків n і початковим станом s0 розглянемо послідовність задач задаючи послідовно n = 1, 2, … при різних s - однокрокову, двокрокову і т.ін. – використовуючи принцип оптимальності, сформульований Р. Беллманом у 1953 р. Принцип оптимальності: У будь-якому стані s системи в результаті деякого числа кроків, на найближчому кроці потрібно вибирати керування так, щоб воно в сукупності з оптимальним керуванням на всіх наступних кроках приводило до оптимального виграшу на всіх кроках, що залишилися, включаючи поточний. Даний принцип вірний, якщо процес керування – без зворотного зв'язку, тобто керування на даному кроці не повинне впливати на попередні кроки. Уведемо деякі додаткові позначення. На кожному кроці будь-якого стану системи sk-1 рішення Хk потрібно вибирати з урахуванням того, як цей вибір впливає на наступний стан sk і подальший процес керування, що залежить від sk, тому що це випливає з принципу оптимальності. Однак є крок, останній, котрий можна планувати оптимально для будь-якого стану sn-1 , виходячи тільки з міркувань цього кроку. Розглянемо n-й крок: sn-1- стан системи до початку n - го кроку, sn = s’ - кінцевий стан, Хn - керування на n -му кроці, fn(sn-1, Хn)- цільова функція (виграш) n - го кроку. Відповідно до принципу оптимальності, Хn потрібно вибирати так, щоб для будь-яких станів sn-1 одержати максимум (мінімум) цільової функції на цьому кроці. Позначимо через Z*n (sn-1) максимум цільової функції - показника ефективності n-го кроку за умови, що до початку останнього кроку система S була в довільному стані sn-1, а на останньому кроці керування було оптимальним. Z*n (sn-1) називається умовним максимумом цільової функції на n-му кроці. Очевидно, що Z*n (sn-1) = max fn(sn-1, Хn) (5.1) {Хn} Максимізація ведеться по всіх припустимих керуваннях Хn. Рішення Хn, при якому досягається Z*n (sn-1), також залежить від sn-1 і називається умовним оптимальним керуванням на n-му кроці. Воно позначається через Х*n (sn-1). Вирішивши одномірну задачу локальної оптимізації по рівнянню (5.1), знайдемо для всіх можливих станів sn-1 дві функції: Z*n (sn-1) і Х*n (sn-1). Розглянемо тепер двокрокову задачу: приєднаємо до n-го кроку (n-1)-й. Для будь-яких станів sn-2, довільних керувань Хn-1 і оптимальному керуванні на n-му кроці значення цільової функції на двох останніх кроках дорівнює: fn-1(sn-2, Хn-1) + Z*n (sn-1) (5.2) Відповідно до принципу оптимальності для будь-яких sn-2 рішення потрібно вибирати так, щоб воно разом з оптимальним керуванням на останньому (n-му) кроці приводило б до максимуму цільової функції на двох останніх кроках. Отже, потрібно знайти максимум виразу (5.2) по всіх припустимих керуваннях Хn-1. Максимум цієї суми залежить від sn-2, позначається через Z*n-1 (sn-2) і називається умовним максимумом цільової функції при оптимальному керуванні на двох останніх кроках. Відповідне керування Хn-1 на (n-1)-му кроці позначається через Х*n-1 (sn-2) і називається умовним оптимальним керуванням на (n-1)-му кроці. Z*n-1 (sn-2) = max {fn-1 (sn-2, Хn-1) + Z*n (sn-1)} (5.3) {Хn-1} У результаті максимізації тільки за однією змінною відповідно до рівняння (5.3) знову виходять дві функції: Z*n-1 (sn-2) і Х*n-1 (sn-2). Далі розглядається трикрокова задача: до двох останніх кроків приєднується (n - 2)-й і т.д. Позначимо через Z*k (sk-1) умовний максимум цільової функції, отриманої при оптимальному керуванні на n-k+1 кроках, починаючи з к-го до кінця, за умови, що до початку к-го кроку система знаходився в стані sk-1. Фактично ця функція дорівнює n Z*k (sk-1) = max ∑ fi (si-1, Хi) {(xk,…xn)} i=k Тоді n Z*k+1 (sk) = max ∑ fi (si-1, Хi) {(xk+1,…xn)} i=k+1 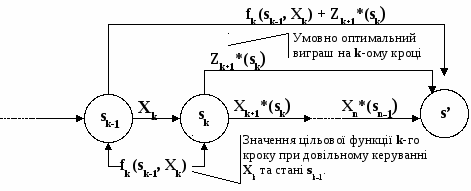 Мал. 5.1. Цільова функція на n-k останніх кроках при довільному керуванні Хk на k-му кроці й оптимальному керуванні на наступних n-k кроках дорівнює fk(sk-1, Хk) + Z*k+1 (sk) Відповідно до принципу оптимальності, Хk вибирається з умови максимуму цієї суми на основі рекурентних співвідношень, що дозволяють знайти попереднє значення цільової функції, знаючи наступне тобто Z*k (sk-1) = max {fk (sk-1, Хk) + Z*k+1 (sk)} (5.4) {Хk} k = n-1, n-2, … 2, 1. Рівняння (5.4) називається рівняннямБеллмана. Керування Хk на k-м кроці, при якому досягається максимум у (5.4), позначається через Х*k (sk-1) і називається умовним оптимальним керуванням на k -му кроці. Якщо з (5.1) знайти Zn*(sn-1), то при k = n-1 з (5.4) можна визначити вираз для Zn-1*(sn-2) і відповідні Х*n-1 (sn-2) вирішивши задачу максимізації для всіх можливих значень sn-2. Після цього з Zn-1*(sn-2) з використанням (5.4) знаходяться рівняння станів. Процес рішення рівнянь (5.1) і (5.4) називається умовною оптимізацією. У результаті умовної оптимізації виходять дві послідовності.
Zn*(sn-1), Zn-1*(sn-2), …, Z2*(s1), Z1*(s0).
Хn*(sn-1), Хn-1*(sn-2), …, Х2*(s1), Х1*(s0). Цей спосіб відповідає рішенню задачі ДП по «зворотній схемі» (алгоритм «зворотного прогону»), коли рішення починається з завершального етапу. Помінявши n-й і 1-й кроки місцями, одержимо «пряму схему» (алгоритм «прямого прогону») рішення задачі ДП. Використовуючи ці послідовності, можна знайти рішення задачі ДП при даних n і s0. За визначенням (5.1) Z1*(s0) – умовний максимум цільової функції за n кроків за умови, що до початку 1-го кроку система була в стані s0, тобто Zmax = Z1*(s0). Після цього, використовуючи послідовність умовно оптимальних керувань, при фіксованому s0 одержуємо Х1* = Х1*(s0), потім, з огляду на відсутність післядії, знаходимо s*1 і підставляємо цей стан у послідовність умовних оптимальних керувань і т.д. Одержуємо: Х1* = Х1*(s0) à s*1 è Х*2 = Х2*(s1)à s*2 è … à s*n-1 è Х*n= Хn*(sn-1). Одержуємо оптимальне рішення задачі ДП: Х*(Х*1, Х*2, … Х*n). Загальна схема застосування методу ДП має такий вид.
а) Zmax = Z1*(s0) і б) по ланцюжку s0 è Х*1 à s*1 è Х*2 à s*2 è … è Х*n-1 à s*n-1 è Х*n à s*n оптимальне керування: Х*(Х*1, Х*2, … Х*n). Приклад 1. Задача розподілу капіталовкладень. На підприємстві розглядаються чотири проекти розширення, що характеризуються величиною прибутку, пов'язаної з реалізацією кожного проекту окремо. Планується здійснити капіталовкладення в розмірі 3 мільйонів гр.о. Знайти такий розподіл капіталовкладень, щоб дістати максимальний прибуток від реалізації всіх проектів.
Рішення. Дану задачу можна вирішити шляхом прямого перебору всіх можливих варіантів рішення. Однак такому способу притаманні недоліки:
Метод ДП дозволяє в значній мірі позбутися цих недоліків. В основу методу покладена ідея поступової покрокової оптимізації. Дана задача розбивається на 4 етапи. Свідомо неоптимальні рішення, отримані на проміжних етапах, відкидаються. Використання інформації про ряд рішень дозволяє в значній мірі скоротити обсяг обчислень. Задача вирішується з застосуванням сіткової моделі. Спочатку визначаються етапи рішення задачі, що пов'язані між собою обмеженнями на сумарний обсяг капіталовкладень. I етап. Засоби вкладаються тільки в перший проект. II етап. Засоби вкладаються в перший і другий проекти разом. III етап. Засоби вкладаються в перший, другий, третій проекти разом. IV етап. Засоби вкладаються в усі чотири проекти. Загальна задача розбивається на підзадачі, що відповідають кожному етапу, не порушуючи при цьому умови допустимості. Позначимо: Х1 – обсяг капіталовкладень розподілених на етапі 1; Х2 – обсяг капіталовкладень розподілених на етапах 1 і 2; Х3 – обсяг капіталовкладень розподілених на етапах 1, 2 і 3; Х4 – обсяг капіталовкладень розподілених на етапах 1, 2, 3 і 4. На кожному етапі знаходиться умовно оптимальне рішення. Умовно оптимальний виграш для вершини 1 II етапу: Z2* (1) = max {0+200; 140+0} = 200. Дуги другого етапу характеризуються величинами Х1 і Х2. Різниця ΔХ2 = Х1 - Х2 - інвестиції в другий проект. Умовно оптимальний виграш для вершини 2 II етапу: Z2* (2) = max {0+320; 140+200; 250+0} = 340. Найкраще рішення для II етапу: Z2* (Х2) = max { Z1* (Х1) + П2}. Найкраще рішення для III етапу: Z3* (Х3) = max { Z2* (Х2) + П3}. ΔХ1 = 0; ΔХ2 = 1; ΔХ3 = 1; ΔХ4 = 1. Розглянута мережна модель називається концептуальною, тому що вона відображає уявний, а не існуючий об'єкт. |
