Мат_методи дослідження операційі. Навчальний посібник Київ 2008 Зміст Анотація 3 План курсу 4 Лекція Вступ. Цілі, критерії, обмеження. 4
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Лекція 2. Лінійне програмування: графічний метод і розробка моделі.Лінійне програмування є найбільш розробленим розділом математичного програмування, який широко застосовується. Це пояснюється такими причинами:
В области электросвязи методами линейного программирования решаются такие задачи:
Основна задача лінійного програмування (ОЗЛП). Основна задача лінійного програмування ставитися в такий спосіб. Є ряд змінних х1, х2, … хn. Потрібно знайти такі невід’ємні значення цих змінних, котрі задовольняють системі рівнянь: a11x1+a12x2+…+a1nxn = b1; a21x1+a22x2+…+a2nxn = b2; . . . . . . . . . . . . . . . . . . . . . am1x1+am2x2+…+amnxn=bm;(2...1) і перетворювали в мінімум функцію W = c1x1+c2x2+…+cnxn,де х1 ≥0; х2≥0; … хn≥0. яка називається цільовою функцією задачі. Припустимим рішенням називається сукупність невід’ємнних х, що задовольняють рівнянням системи. Оптимальним називається ті з припустимих рішень , що перетворює в мінімум лінійну цільову функцію. Якби на область зміни перемінних не накладалося ніяких обмежень, те пошук екстремума лінійної цільової функції не мав би змісту. Задачі лінійного програмування вирішуються в два етапи:
Властивості припустимих рішень. При розгляді властивостей рішень систем лінійних рівнянь виду (2.1) можливі три випадки: m=n, m>n, m Якщо число рівнянь m дорівнює числу перемінних n, і визначник системи (2.1) не дорівнює 0, то система має єдине рішення. Якщо всі змінні системи невід’ємнні, те це рішення буде припустимим. Оскільки таке рішення єдине, те воно буде й оптимальним. У класичних задачах лінійного програмування, як правило, m>n. У таких задачах, якщо система сумісна, те існує нескінченна множина її рішень. При цьому m-n змінним можна надавати довільні значення в рамках обмежень, і такі змінні називаються вільними. Інші m змінних можуть бути виражені через вільні і називаються базисними. Базисні змінні вибираються за допомогою спеціального алгоритму. Якщо число вільних змінних не більш 2-х, те задачу можна вирішити графічно. 1-й крок при графічному методі рішення полягає в геометричному поданні припустимих рішень, тобто побудови області припустимих рішень (ОПР), у якій одночасно задовольняються всі обмеження моделі. 2-й крок полягає в знаходженні оптимального рішення (у тому випадку, якщо воно існує). Розробка моделей лінійного програмування. Термін «розробка» означає побудову моделей лінійного програмування для практичних задач. Розробка моделі містить у собі три етапи:
Приклад. Оптимізація побудови мережі телевізійного віщання. Для побудови мережі телевізійного віщання на території площею 30 000 тис. кв. км пропонується використовувати телевізійні станції 2-х типів із загальною споживаною потужністю не більш 125 квт. Загальна чисельність штату на всіх станціях не винна перевищувати 24 шт. од. Параметри станцій наведені в таблиці.
Задана площа обслуговування враховує деяке взаємне перекриття зон обслуговування. Потрібно визначити оптимальне число станцій типів 1 і 2 при, якому приведені витрати на всю мережу будуть найменшими. Рішення. Шукане число станцій 1 і 2 приймаємо за керовані змінні х1 і х2 відповідно Х = (х1,х2). Сумарні витрати на мережу W(X) = 15x1 + 200x2. Оптимізаційна математична модель: знайти невід’ємнні значення зінних х1 і х2, при яких цільова функція W(х1,х2) = 15x1 + 200x2 è min (2.2) і задовольняють обмеженням: 500 х1 + 10000х2 ≥ 30000 0,15 х1 + 8х2 ≤ 24 0,63 х1 + 55х2 ≤ 125 Задача вирішується методом лінійного програмування (ЛП). Приводимо її до ОЗЛП у такий спосіб: в усіх нерівностях перенесемо в ліві частини постійні величини і дві останніх нерівності помножимо на –1, помінявши знаки нерівностей: 500 х1 + 10000х2 - 30000 ≥ 0 - 0,15 х1 - 8х2 + 24 ≥ 0 - 0,63 х1 - 55х2 + 125 ≥ 0 введемо нові невід’ємнні змінні х3, х4, х5: х3 = 500 х1 + 10000х2 - 30000 ≥ 0 х4 = - 0,15 х1 - 8х2 + 24 ≥ 0 х5 = - 0,63 х1 - 55х2 + 125 ≥ 0 (2.3) Одержали обмеження у вигляді рівностей і звели задачу до пошуку мінімуму цільової функції. Розглянута задача являє собою класичну задачу лінійного програмування, де загальне число змінних n=5, кількість базисних змінних m=3, кількість вільних змінних k=n-m=2. Оскільки k=2 , то рішення задачі можна знайти графічно. Умови невід’ємності змінних обмежують область їхніх припустимих значень першим квадрантом (тобто частиною площини, розташованої над віссю х1 і зправа від осі х2). Інші границі простору не відбиті на площині Х1, Х2. Прямі лінії будуються по рівняннях системи (2.3). Надамо базисним змінним найменшого можливого значення х3=х4=х5=0 і побудуємо відповідні прямі. Для рівняння х3=0 відрізки відтинаються прямої на осях координат складуть відповідно: при х2=0 х1=30000/500=60 при х1=0 х2=30000/10000=3 З одному боку від необмеженої прямої (вправо нагору) значення змінної х3 будуть позитивними, з іншого - негативними. Нанесемо на малюнок відрізки, що відповідають припустимим (позитивним) значенням змінних. Ту ж процедуру проробимо для рівнянь х4 = 0 і х5 = 0. Для х4 = 0 при х2 = 0 х1 = 160; при х1 = 0 х2 = 3. Для х5 = 0 при х2 = 0 х1 = 198,41; при х1 = 0 х2 = 2,27. Частина площини, що задовольняє всім обмеженням, називається областю припустимих рішень (ОПР). Шукана область припустимих рішень показана на малюнку. На малюнку ця область заштрихована; її вершини позначені буквами ABCD (Мал.2.1). Після завершення 1-го етапу рішення (побудови ОПР) необхідно знайти таку крапку цієї області, що забезпечить виконання умови (2.2), тобто є рішенням задачі. Для цього цільову функцію представимо у вигляді додаткового обмеження: W - 15x1 - 200x2 ≥ 0. Зобразимо його прямою W: W - 15x1 - 200x2 = 0. (2.4) Мінімальне значення W прийме, якщо пряма, що її представляє, торкнеться ОПР у самій лівій її частині - у точці А чотирикутника ABCD. При збільшенні W (2.4) пряма переміщається вправо. Крапку торкання прямої W (2.4) можна визначити вирішивши систему рівнянь для х3 = 0 і х5 = 0 з (2.3). У результаті одержуємо х1 = 20 і х2 = 2. Звідси випливає, що W = 700. Координати крапки А (20; 2) і є рішенням задачі. У розглянутому випадку оптимальне рішення – єдине. При W < 700 пряма W лежить поза ОПР, тобто жодна з її точок не є рішенням. 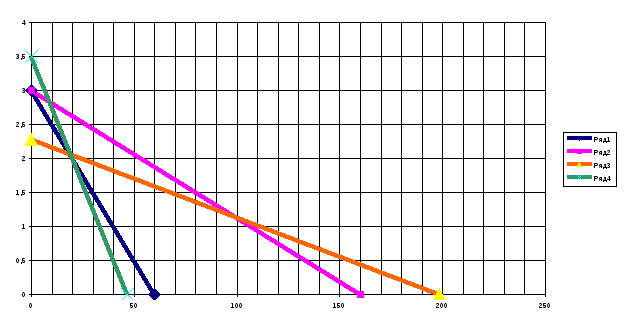  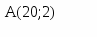   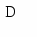 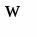 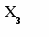 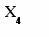 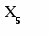 Мал. 2.1. Мал. 2.1.Можливі й інші ситуації. Якби пряма W збіглася з прямою AD, мі малі б нескінчену множину рішень відповідних крапкам, що лежати на відрізку AD (включаючи крапку А). З іншого боку, деякі задачі можуть і не мати рішення через несумісність обмежень (2.3) – для них відсутня ОПР. У нашій задачі це могло вийти, наприклад, при виділенні дуже малого числа штатних одиниць чи надмірного збільшення території, що обслуговується, при незмінності інших вимог. Зауважимо, що змінні х1 і х2 реально можуть мати тільки цілочислові рішення. У дійсності припустимі рішення відповідають дискретній множині крапок в ОПР. У подібних випадках точні рішення дають спеціальні методи ЛП. Тема 3. |
