Мат_методи дослідження операційі. Навчальний посібник Київ 2008 Зміст Анотація 3 План курсу 4 Лекція Вступ. Цілі, критерії, обмеження. 4
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Лекція 7. Динамічне програмування. Прокладення траси.Приклад 2. Задача прокладення траси. Нехай є мережа пунктів, які можна зв'язати між собою відрізками траси (лінійними спорудженнями) із заданими витратами на прокладку траси між сусідніми пунктами. Знайти оптимальну трасу прокладки лінійних споруджень з пункту А в пункт В таким чином, щоб вартість лінійних споруджень була мінімальною. Рішення. Схему розташування пунктів можна подати у вигляді сіткової моделі прямокутної форми, вузлами якої є пункти, що з'єднуються, а над дугами вказуються вартості прокладки ділянок траси між сусідніми пунктами. Отже на сітковій моделі ділянки траси можуть розташовуватися в двох напрямках (Y і Z). Рішення задачі розбивається на 5 послідовних етапів. 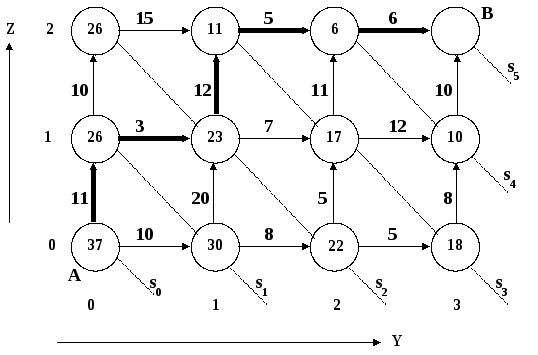 При рішенні використовується алгоритм «зворотного прогону» від кінцевого пункту В до початкового пункту А. Під рішенням на кожному етапі розуміється вибір напрямку, по якому прокладається чергова ділянка траси. Вартість прокладки називається виграшем. Умовно оптимальний виграш позначається W*. Значення W* будемо записувати у відповідні вершини (вузли), а обрані напрямки – позначати стрілками. Етап 5. Вершина (2, 2) Х*=Y W*=6 Вершина (3, 1) Х*=Z W*=10 Етап 4. Вершина (1, 2) Х*=Y W*=11 Вершина (2, 1) Х*=Z W*=17 Вершина (3, 0) Х*=Z W*=18 Етап 3. Вершина (1, 1) Х*=Z W*=23 -суміжна Вершина (0, 2) Х*=Y W*=26 Вершина (2, 0) Х*=Z W*=22 Етап 2. Вершина (0, 1) Х*=Y W*=26 Вершина (1, 0) Х*=Y W*=30 Етап 1. Вершина (0, 0) Х*=Z W*=37 – оптимальний виграш. Після знаходження величини оптимального виграшу визначається топологія траси: А(0, 0) à (0, 1) à (1, 1) à (1, 2) à (2, 2) à B(3, 2) Тема 6. Лекція 8. Сіткове планування та управління (СПУ). Сіткові графіки.Система методів сіткового планування і керування (СПУ) орієнтована на оптимізацію планування і керування великомасштабними комплексами робіт: у будівництві і реконструкції, у наукових дослідженнях, при конструкторській і технологічній підготовці виробництва, при проектуванні нових видів виробів та ін. шляхом застосування мережної моделі. Під комплексом робіт (комплексом операцій, проектом) мають на увазі сукупність різноманітних робіт, здійснюваних для рішення визначеної задачі. Сіткова модель являє собою план виконання деякого комплексу взаємозалежних робіт (операцій), заданого в специфічній формі сітки, графічне зображення якої називається сітковим графіком. Перші системи, що використовують сіткові графіки, були розроблені і застосовані в США в 50-х роках ХХ ст. Наприклад, система СРМ (Critical Path Method – метод критичного шляху) застосовувалася при керуванні будівельними роботами; система PERT (Program Evaluation and Review Technology – метод оцінки й огляду програм) – при створенні систем «Поларис». СПУ дозволяє:
Головними елементами сіткової моделі є події і роботи. Термін робота використовується в СПУ в декількох змістах. По-перше, це дійсна робота – протяжний у часі процес, що вимагає витрат ресурсів (праці, матеріальних ресурсів, часу). По-друге, це очікування – протяжний у часі процес, що не вимагає витрат праці (наприклад, сушіння після фарбування, твердіння бетону й ін.). По-третє, це залежність, чи фіктивна робота – логічний зв'язок між двома чи декількома роботами (подіями), які не потребують витрат праці, матеріальних чи ресурсів часу. Вона вказує, що можливість виконання однієї роботи безпосередньо залежить від результатів іншої. Тривалість фіктивної роботи дорівнює нулю. Подія – це момент завершення якого-небудь процесу, що відбиває окремий етап виконання проекту (комплексу робіт). Подія може здійснитися тільки тоді, коли закінчаться всі роботи, що їй передують. Подія має двоїстий характер: для всіх безпосередньо попередніх їй робіт воно є кінцевою, а для всіх безпосередньо наступних за нею – початковою. Вважається, що подія не має тривалості, тобто здійснюється як би миттєво. Серед подій сіткової моделі виділяють вихідна і завершальна події. Вихідна подія не має попередніх робіт і подій. Завершальне подія не має наступних робіт і подій. Події на сітковому графіку (чи на графі), зображуються колами (вершинами графа), а роботи – стрілками (орієнтованими дугами), що показують зв'язок між роботами. Фрагмент сіткового графіка наведений на мал.6.1. М 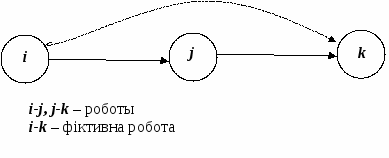 ал. 6.1. ал. 6.1.Порядок і правила побудови сіткових графіків. Сіткові графіки складаються на початковому етапі планування. Спочатку планований процес розбивається на окремі етапи (роботи), складається перелік робіт і подій, визначаються логічні зв'язки між ними і послідовність виконання, за роботами закріплюються відповідальні виконавці. Потім складається (зшивається) сітковий графік. Послідовність робіт на сітковому графіку називається шляхом. Сума витрат часу на виконання робіт, що лежать на деякому шляху називається довжиною цього шляху. Повний шлях – це будь-який шлях, початок якого збігається з вихідною подією сіткового графіка, а закінчення – із завершальним. Критичним шляхом називається найбільш тривалий повний шлях сіткового графіка. Критичними називаються також події і роботи, розташовані на критичному шляху. При побудові сіткового графіка необхідно дотримувати наступні правила:
Після побудови першого варіанта сіткового графіка події нумерують ліворуч праворуч. Потім сітковий графік упорядковують. Упорядкування сіткового графіка полягає в такому розташуванні подій і робіт, при якому для будь-якої роботи попередня їй подія розташована лівіше і має менший номер у порівнянні з завершальною для цієї роботи подією. Іншими словами, в упорядкованому сітковому графіку всі стрілки-роботи спрямовані зліва направо: від подій з меншими номерами до подій з більшими номерами. При упорядкуванні сіткового графіка місце розташування його малюнка попередньо розбивається на вертикальні області. Після цього в лівій області малюнка розміщується вихідна подія сіткового графіка і йому привласнюється перший номер порядкової нумерації. Потім ця подія разом з вихідними з неї роботами уявно викреслюється з вихідного неупорядкованого графіка. Події, що залишились без вхідних робіт, розміщуються в другій області і їм привласнюються наступні порядкові номери. Потім ці події, разом з роботами, що з них виходять уявно викреслюються з неупорядкованого графіка, а події, що залишилися без вихідних робіт, розміщуються в наступній області, і їм привласнюються наступні порядкові номери, і так далі, до розміщення і присвоєння номера завершальній події сіткового графіка. Часові параметри сіткових графіків. Часові параметри подій.
t pj = max { t pi + tij }, де tij - тривалість роботи i-j.
t пi = min { t пj - tij }, де tij - тривалість роботи i-j.
R i = t пi - t pj. Часові параметри подій зводяться в таблицю. Часові параметри робіт.
R ij = t пj - t pi - tij ; чи R ij = t ппij - t pпij ; чи R ij = t пзij - t pзij.
Rв(i,j) = t рj - t рi - tij ; чи Rв(i,j) = R(i,j) - R(j).
Rн(i,j) = t рj - t пi - tij ; чи Rн(i,j) = R(i,j) - R(i) - R(j) ; чи Rн(i,j) = Rс(i,j) - R(i). Часові параметри робіт зводяться в таблицю. Для всіх робіт критичного шляху збігаються ранні і пізні терміни початку робіт і відповідно ранні і пізні терміни їхнього закінчення. Тривалість критичного шляху збігається з ранніми і пізніми термінами здійснення кінцевої події сіткового графіка. Топологія критичного шляху визначається тим, що він проходить через події і роботи, що не мають резервів часу. Зауваження:
М 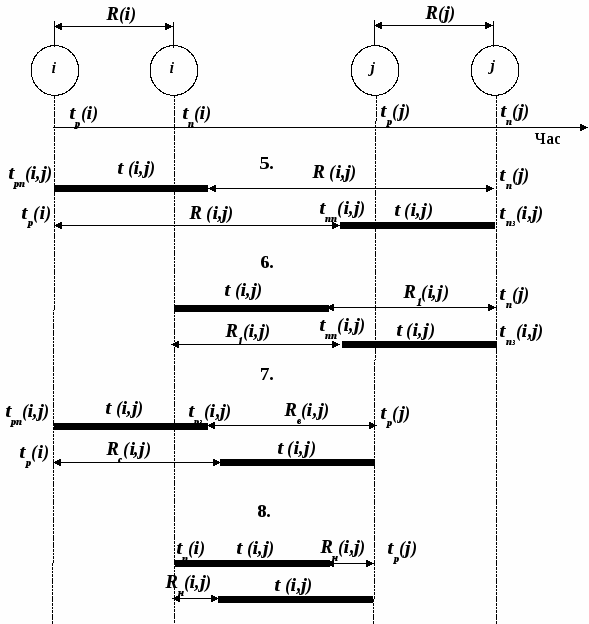 ал. 6.2. ал. 6.2. |
