Назар аудары_ыз!. Назар аударыыз!
 Скачать 357 Kb. Скачать 357 Kb.
|
|
Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 3. МАТЕМАТИКАЛЫҚ СТАТИСТИКА ӘДІСТЕРІНІҢ КӨМЕГІМЕН БОЛЖАМДАРДЫ ДӘЛЕЛДЕУ МӘСЕЛЕСІН ШЕШУДІҢ ЖАЛПЫ ПРИНЦИПТЕРІ Дәріс тезистері Статистикалық болжамдар Статистикалық болжамадар келесі түрлерге бөлінеді: нөлдік болжам; альтернативты болжам; бағытталған болжамдар; бағытталмаған болжамдар. Нөлдік болжам дегеніміз – айырмашылықтың болмауының болжамы. Альтернативты болжамдар – айырмашылықтардың маңызы жөніндегі болжам. Бағытталған болжамдар гипотезы – Х1 мағнасы Х2 мағнасынан аспайтындығы туралы болжам. Бағытталмаған болжамдар Х1 мағнасының Х2 мағнадан айрықша немесе бірдеу болатынын көрсетеді. Бірінші топ ішіндегі адамдардың бір белгі бойынша (мысалы, әлеуметтік батылдық бойынша) жекедара көрсеткіштері екінші топтағы көсеткіштерден артық болғанын байқасаңыз, екі топ арасындағы айырмашылықты тексеру үшін бағытталған болжамды пайдалану керек. «А» тобында эксперимент әсерінен пайда болған өзгерістес «Б» тобынандағы өзгерістерден асып түсетіндігін дәлелдеу үшін бағытталған болжам құрастыру керек. «А» тобы мен «Б» тобының белгі таралу көрсеткіштерді салыстырғандн бағытталмаған гипотезелар қолданылады. Болжамды тексеру статистикалық баға мен айырмашылық критерийлар көмегімен өткізіледі. 5.Статистикалық критериилар Статистиаклық критериилар (белгілер) – берік іс-әрекетті, яғни дәл болжамды қабылдауын және қата болжамды қайрып тастауын жоғары ықтималдықпен қамтамасыз ететін негізгі шешуші ережелер. Параметрлік критериилар – есеп формуласына тарау параметрлерін, яғни орта шама мен дисперсияларды қосатын критериилар. Параметрлік емес критерии – тек қана жиілік пен ранг түсініктерді пайдаланады. Статистикалық мәнділік деңгейі айырмашылықты мәнді деп ойлап, олардың кездейсоқ болып шығатананың ықтималдығы. Осы деңгейлер 5% и 1%ттік болады. 5% немесе р≤0,05 мәнділік деңгей айырмашылықтарды сенімді деп санағанымызды, бырақ олардың 0,05 сенімсіз болып шығатындығының ықтималдығы. Критерийдың қуаттылығы деп оның айырмашылықтарды айқындайтын қабілеті. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 4. ЗЕРТТЕЛІП ЖАТҚАН БЕЛГІНІҢ ДЕҢГЕЙІНДЕГІ ӨЗГЕШЕЛІКТЕРДІ АЙҚЫНДАУ. ТӘУЕЛСІЗ ТАҢДАМАЛАР ҮШІН ДИСПЕРСИОНДЫ АНАЛИЗ. Дәріс тезистері. Комплекстер құрастыру. Әрбір зерттенушіге сыналатын белгілердің барлығы көрсетілетін бөлек карточка ашқан жөн. Карточкаларды дисперсиялық комплекстерге кіргізуге болады. Олардың көмегімен факторлардың көптеген градацияларын қалыптастыру мүмкін. Әрбір ячейкада бірдейбақылау саны орналасса, мұндай комплексті бірқалыпты деп атайды. Комплекстің бірқалыптылығы әрбір ячейкаға (ұяға) тең емес дисперсия санын орналастыруға мүмкіншілік береді. Дисперсиялық анализ параметриялық әдістер тобына жатады; сондықтан оны тек қана белгі тарауы нормаға сай жағдайларында қолдануға болады. Есептеуді жеңілту үшін эмпирикалық нәтижелерді қайта өзгерту әдістері: бақыланған мағыналардың бәрін бір ғана k санына бөлуге болады; оларды бір ғана k санына көбейтуге болады; мағыналардан А санын алуға болады; қос өзгерту жасауға болады: әрбір мағынадан А санын алып тастап, қалғанын басқа k санына бөледі. Бірфакторлық дисперсиялық анализ өзгеріп жатқан фактордың шарттары мен гпрадациялары (үштен кем болмайтын) әсерінен нәтжелік белгінің өзгеруі зерттелінге кезде қолданылады. Біріншіден зерттеу нәтижелерін жекедара мағыналар бағаналар ретінде белгілейді. Сосын жеке көрсеткіштерді қосып, сумманы квадратқа көшіру керек. Бірфакторлық әдістің кемістігі: Дисперсиялық анализдың осы түрінде екіден кем емес градациялар қолданылады, әрбір градацияда екі адамнан кем болмауы қажет; Дисперсия комплексінің әрбір ұясында дисперсия теңдігі ережесы орыгдалуы керек. Нәтижелік белгі зерттелген выборкада нормаға сай таралуы керек. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 5. ЗЕРТТЕЛІП ЖАТҚАН БЕЛГІНІҢ ДЕҢГЕЙІНДЕГІ ӨЗГЕШЕЛІКТЕРДІ АЙҚЫНДАУ. ТӘУЕЛСІЗ ТАҢДАМАЛАР ҮШІН СТЬЮДЕНТТІҢ Т-КРИТЕРИЙІ. Дәріс тезистері. Болжамдарды дәлелдеудің екінші схемасы – екі топты өзара салыстыру және олардың арасындағы өзгешеліктердің барын дәлелдеу. Бұл схеманы жүзеге асыру статистикалық критерийлерді қолданудың көмегімен жүреді. Психолог өз зерттеулерін статистикалық өңдеуге көшуден бұрын өз материалына сәйкес келетін - параметрлік немесе параметрлік емес әдістердің бірін таңдау керек. Параметрлік әдістерді қолданудың артықшылықтары көп болғанмен, оларды тек интервалдық немесе тең қатынастар шкаласында өлшенген берілгендер үшін ғана қолдана аламыз. Берілгендердің екі жиынына жататын орталық мәндерді салыстыру үшін және орталық мәндер бір бірінен статисткалық мәнді түрде өзгеше екенін шешу үшін, көбінесе, Стьюденттің t-критерийі қолданылады. Бұл әдіс параметрлік әдістер қатарына жатады. Оның формуласы төмендегідей :
X1 бір таңдаманың үлкен арифметикалық ортасы X2 келесі таңдаманың кішірек арифметикалық ортасы, m21 , m22 салыстырылып жатқан екі таңдаманың сәйкес орталық мәндерінен жеке мәндердің ауытқуының интеграцияланған көрсеткіштері. Олар келесі формуламен есептелінеді:
мұнда σ1 , σ2 сәйкес таңдамалардың стандартты ауытқулары n1, n2 сәйкес таңдамалардағы айнымалылардың мәндерінің саны. Стьюденттің t- критерийінің экспериментальды мәнін есептеп болған соң, оны таблицадағы шектік мәнмен салыстырамыз. Егер tэксп ≥ tтабл, онда Н0 болжамы теріске шығарылып, Н1 .қабыл алынады. Егер tэксп ≤ tтабл , онда Н0 қабыл алынып, Н1 теріске шығарылады. Н0 , Н1 статистикалық болжамдар, мұнда Н0 әрқашан өзгешеліктер немесе өзгерістердің кездейсоқтығын көрсетеді, ал Н1 - өзгешеліктердің статистикалық мәнділігі туралы айтады. Кез келген статистикалық болжамдарды тексергенде бір жаққа қарай ауған шешім ешқашан толық сеніммен қабылданбайды. Әрқашан дұрыс емес шешім қабылдау ықтималдылығы (зерттеушінің қадағалауымен) болады. Бұл шама мәнділік деңгейі деп аталады және статистикалық қорытындыда көрсетіледі. Мысал ретінде статистикалық қорытындыдан үлгі келтіруге болады: «Сөйтіп, ... (салыстырылатын параметрлар көрсетіледі) бойынша топтар арасында... (таңдамалар сипатталады) Стьюденттің t-критерийіне сәйкес 5% деңгейде мәні бар статистикалық өзгешеліктер байқалады (t = 3,24, ρ = 0,05)». Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 6. ӨЗГЕШЕЛІКТЕР СТАТИСТИКАСЫ. МАННА-УИТНИДІҢ U - КРИТЕРИЙІ Дәріс тезистері Критерий екі таңдама арасындағы қандай да бір белгінің деңгейі бойынша өзгешеліктерді бағалау үшін арналған. Ол саны аз таңдамалар арасындағы өзгешеліктерді айқындайды, мұнда n1•n2≥3 немесе n1=2, n2≥5. Критерийді қолданудың бірнеше тәсілі бар, және осы тәсілдерге сәйкес келетін бірнеше шектік мәндердің кестелері бар. Бұл әдіс екі қатар мәндер арасындағы қиылысатын зоналар жеткілікті дәрежеде аз ба екендігін анықтайды. Қиылысатын мәндер аз болған сайын, айырмашылықтар рас екендігі жоғарлай түседі. Кейде бұл өзгешеліктер екі таңдаманың орналасуындағы өзгешеліктер деп аталады. U критерийдің эмпирикалық мәні қатарлар арасындағы сәйкестік зонасы қаншалықты үлкен екендігін бейнелейді. Uэмп, аз болған сайын, айырмашылықтар рас екендігі соншалықты жоғары ықтималды болады. Мұнда n1 -1 таңдамадағы сыналушылардың саны; n2 – 2 таңдамадағы сыналушалар саны; Тх – екі рангтық қосындылардың ішіндегі үлкені; nх – рангтар қосындысы үлкенірек топтағы сыналушылардың саны. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 7. ӨЗГЕШЕЛІКТЕР СТАТИСТИКАСЫ. КРУСКАЛА-УОЛЛИСТІҢ Н - КРИТЕРИЙІ Дәріс тезистері Критерий қандай да бір белгінің деңгейі бойынша бір мезгілде үш, төрт және т.с.с. таңдамалар арасындағы өзгешеліктерді бағалауүшін арналған. Ол белгінің деңгейі бір топтан екіншісіне өткенде өзгеретіндігін анықтауға мүмкіндік береді. Бірақ бұл өзгерістердің бағытын көрсетпейді. Н критерийі байланысты емес таңдамалар үшін бір факторлы дисперсионды анализдің параметрлік емес аналогтық әдісі ретінде қарастырылады. Баолық индивидуалды мәндер бір үлкен таңдама ретінде рангыленеді. Сосын барлық индивидуалды мәндер алғашқы таңдамаларға біріктіріледі. Сосын әрбір таңдама бойынша сол мәндердің алған рангтарын санаймыз. Егер таңдамалар арасындағы өзгешеліктер кездейсоқ болсарангтардың қосындысы ношалықты мәнді түрде өзгешеленбейді. Себебі таңдамалар арасындағы рангтардың жоғары төмен мәндері біртекті үлестіріледі. Ал егер бір топта рангтардың төмен мәндері басым болып, екіншісінде үлкен мәндері басым болса, үшіншісінде орташа мәндер асып кетсе, онда Н критерийдің көмегімен осы айырмашылықтарды көрсете аламыз. 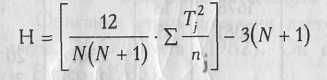 Мұнда, N – обіріктірілен таңдамадағы сыналушылардың жалпы саны; n – әрбір топтағы сыналушылардың саны; Т –әрбір топтағы рангтар қосындысы. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 8. ЗЕРТТЕЛІП ЖАТҚАН БЕЛГІНІҢ ДЕҢГЕЙІНДЕГІ ЫҒЫСУЛАРДЫ АЙҚЫНДАУ. БАЙЛАНЫСТЫ ТАҢДАМАЛАР ҮШІН ДИСПЕРСИОНДЫ АНАЛИЗ. Дәріс тезистері Бұл әдіс бір ғана сыналушылар таңдамасына фактордың әртүрлі градациялары мен шарттары ететін әсерін зерттеу кезінде пайдаланады. Оның ерекшелері: Фактордың үштен кем емес градация саны қажет, әрбір градация екіден кем емес адамдар санына әсер етуі керек.; Комплекстың әрбір ұясында дисперсия теңдігі ережесі орындалуы қажет; Нәтижелік белгі нормаға сай таралуы керек F кртерий үшін аралық шамаларды есептеу
Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 9. ЗЕРТТЕЛІП ЖАТҚАН БЕЛГІНІҢ ДЕҢГЕЙІНДЕГІ ЫҒЫСУЛАРДЫ АЙҚЫНДАУ. БАЙЛАНЫСТЫ ТАҢДАМАЛАР ҮШІН СТЬЮДЕНТТІҢ T-КРИТЕРИЙІ Дәріс тезистері Екі топ арасындағы орташа бағалардың өзгешелігі айнымалылардың топішілік вариациясынан (дисперсия) тәуелді. Әрбір топ үшін осы мәндердің өзгешеліктерінен тәуелді, топтық орташалар арасындағы айырмашылық тәуелді және тәуелсіз айнымалылар арасындағы күшті немесе әлсіз тәуелділік дәрежесін көрсетеді. Тәуелді таңдамалар үшін t-критерийдің мақсаты практикада жиі пайда болатын топішілік вариацияның (немесе қатенің) көзі оңай анықталып, анализден алынып тасталатын жағдайларда пайдалы. Тәуелсіз таңдамалар үшін t-критерийдің теоретикалық негіздері тәуелді таңдамалар үшін арналған критерийлерге қатысты болады. Бұл жұпталған айырмалар қалыпты үлестірілген болу керек деген сөз. Егер бұл шарт орындалмаса альтернативті параметрлік емес критерийлердің біреуімен қолдану керек. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 10. ЫҒЫСУЛАР СТАТИСТИКАСЫ. ВИЛКОКСОНЫҢ Т - КРИТЕРИЙІ Дәріс тезистері Критерий сыналушылардың бір таңдамасында екі түрлі жағдайларда өлшенген көрсеткіштерді салыстыру үшін қолданады. Бұл өзгерістердің бағытын ғана емес, сонымен бірге олардың айқындығын да көрсете алады. Оның көмегімен біз көрсеткіштердің ығысуы бір жақ бағытта екінші жаққа қарағанда анағұрлым қарында ма екендігін анықтаймыз. Бұл критерийді белгілер ең болмағанда тәртіптік шкалада өлшенген болу керек. Бірінші және екінші өлшемдерден кейінгі ығысуларды тәртіптеп шығу керек. Бұл үшін ол жеткілікті кең диапазонда вариациялану керек. Әдістің мәні бойынша біз ығысуларды белгілі бір бағытта абсолютты шамалары бойынша салыстырамыз. Бұл үшін барлық ығысулардың абсолютты мәндерін рангтаймыз. Сосын рангтарды қосамыз. Егер ығысулар оңға және теріс жаққа қарай кездейсоқ болса, онда олардың абсолютты мәндерінің рангтарының қосындысы біршама ұқсас болады. Егер бір жаққа қарай ығысу қарқыны басым болса, онда қарама қарсы жаққа қарай ығысулардың абсолютты мәндерінің рангтарының қосындысы кездейсоқ өзгерістермен салыстырғанда анағұрлым төмен болады. Ең әуелі типтік ығысу деп жиірек кездесетін бағыттағы ығысуды атаймыз, ал типтік емес, немесе сирек кездесетін жаққа арай ығысуды айтамыз. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 11. ЫҒЫСУЛАР СТАТИСТИКАСЫ. ФРИДМАННЫҢ Χ2R КРИТЕРИЙІ Дәріс тезистері Критерий χ2r бір таңдаманың үш немесе одан да көп жағдайда өлшенген көрсеткіштерін салыстыру үшін қолданылады. Критерий көрсеткіш шамасы жағдайдан жағдайға қарай өзгеретіндігін көрсетуге мүмкіндік береді, бірақ мұнда өзгерістің бағытын көрсете алмайды. Мұнда ығысулардың абсолютты мәндерін рангтамаймыз. Берілген сыналушының 1,2,3 және т.с.с. өлшеу процедураларында алынған индивидуалды мәндерін рангтаймыз. Мәселен, егер сыналушы бірінші өлшеуде графикалық лабиринтты 54 сек өтіп шықса, екінші өлшеуде 42 сек жіберсе, үшінші өлшеуді 63 сек жұмсаса, сыналушының алынған мәндеріне сәйкес 2,1,3 рангтарын алады. Екінші өлшеуде алынған ең төмен бағаға 1 ранг береміз. Бірінші өлшеуде алған орташа мәнге 2 ранг береміз, алынған ең үлкен мәнге 3 ранг береміз. Барлық мәндер рангталып шыққан соң , әрбір жасалған өлшем бойынша рангтардың қосындысын санаймыз. Егер түрлі жағдайларда алынаған белгінің мәндері арасындағы өзгешеліктер кездейсоқ болса, түрлі шарттар бойынша алынған рангтардың қосындысы біршама ұқсас деген сөз. Ал егер белгінің мәндері түрлі жағдайда қандай да бір заңдарға сәйкес өзгеретін болса, рангтардың қосындысы бір бірінен дәйекті түрде өзгешеленеді. χ2r критерийдің эмпирикалық мәні рангтардың қосындысы қаншалықты өзгеше екендігін көрсетеді. χ2r, Критерийдің эмпирикалық мәні жоғары болған сайын соғұрлым рангтар қосындысының мәнді өзгешеліктерін бейнелейді. Егер χ2rшектік мәнге жақын болса немесе одан анағұрлым жоғары болса, өзгешеліктер статистикалық дәйекті болып келеді. | |||||||||||||||||||||||||||||||||||||||||||||||
