Назар аудары_ыз!. Назар аударыыз!
 Скачать 357 Kb. Скачать 357 Kb.
|
|
1.7. Әдебиет тізімі: Негізгі әдебиет: Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М., 1976 Сидоренко Е.В. Методы математической обработки в психологии. СПб., 1996 Суходольский Г.В. Основы математической статистики для психологов. СПб., 1998 Қосымша әдебиет Артемьева Е.Ю. Сборник задач по теории вероятностей и математической статистики для психологов. М., 1969 Плохинский Н.А. Биометрия. М., 1970 Пустыльник Е.И. Статистические методы анализа и обработки наблюдений. М., 1968 Справочник по прикладной статистике: в 2-х т. М., 1989-1990 Захаров В.П. Применение математических методов в социально-психологических исследованиях. Л., 1985 Рунион Р. Справочник по непараметрической статистике. М., 1982 Холлендер М., Вулф Д.А. Непараметрические методы статитики. М., 1983 Крылов В.Ю. Геометрическое представление данных в психологических. М., 1990 Дрейпер М., Смит Г. Прикладной регрессионный анализ. М., 1973 1.8. Баға жөніндегі ақпарат: Білімді бағалау шкаласы:
1.9. Курстың саясаты. Студенттер міндетіне сабақтарға қатысу, пән бойынша тапсырмаларды графикке сәйкес орындау және әдебиетпен кітапхана мен интернет-залында өзіндік жұмыстар орындау. Сабаққа кешігу, келмеу және аудиторияда басқа адамдардың білім алуына кедергі келтіретін жүріс-тұрыс үшін жауапкершілік «ҚарМУ-дың ішкі ережелерімен» анықталады. Егер студентт жазба жұмыстарын белгіленген уақыттан кеш берсе, білім рейтингі 10 процентке төмендейді. Студенттің өзінің қатысуынсыз қорытынды бақылау өткізілмейді. Емтиханға келмеу жағдайлары ҚарМУ-дың оқу процесін ұйымдастыру ережелерімен реттеледі. 2.ПӘН БОЙЫНША ОҚУ-ӘДІСТЕМЕЛІК МАТЕРИАЛДАР 2.1. Курстың тақырыптық жоспары (барлығы 3 кредит)
2.2. Дәрістік сабақтардың тезисері Дәріс 1. СИПАТТАУШЫ СТАТИСТИКА. ӨЛШЕМ МӘСЕЛЕСІ. Дәріс тезистері. Берілгендер мен белгілер. Бұл өлшенетін психологиялық құбылыстар. Мұндай құбылыстар ретінде есепті шешу уақыты, жіберілген қателердің саны, үрейлену деңгейі, интеллект, агрессивті реакциялардың қарқындылығы, социометриялық статустың көрсеткіштері т.б. айнымалылар бола алады. Белгі мен айнымалы ұғымдары өзара ауыстырылып, қолданыла береді. Кейде олардың орнына көрсеткіш немесе деңгей деген ұғымдар қолданылуы мүмкін. Көрсеткіш пен деңгей деген ұғымдар белгінің санмен өлшенуін білдіреді. Мәселен, интеллект деңгейінің жоғарылығы, үрейлену деңгейінің төмендігі т.б. Айнымалылар деп адамдар немесе заттардың (объекттердің) сипаттамаларын айтамыз. Мәселен, жасы, салмағы, реакция уақыты, оқу тездігі, балалар саны т.б. Кейбір айнымалылар үздіксіз, кейбіреулері дискретті (жеке мәндерге ғана ие бола алады) мәнге ие болады. Үздіксіз айнымалылырды дәл, нақты өлшеу мүмкін емес. Себебі өлшеу арқылы біз айнымалылардың мәнін үзіп жібереміз. Шынайы өмірде уақыт бойында тұрақты белгілеп қоятын орын болмайды. Сондықтан үздіксіз айнымалылардың мәні жанамалы сипатқа ие. Ол өлшеу процессінің нәтижесі болып келеді. Жанамалы мен нақты айнымалының мәндері беттеспеуі мүмкін. Бірақ біріншісі екіншісінің шектелуіне әкеледі. Мәселен, егер адамның бойы 157 см болса, онда оның шын мәніндегі бойы 156,5 мен 157,5 см аралығында жатады. Кез келген үздіксіз айнымалының мәні өлшем процессінің дәлдігімен анықталады. Өлшем процедурасының сезімталдылығы сандық шкаланың минимальды бірлігімен беріледі. Дәл мәннің шектерін анықтау жолы табылғанмәннің жан-жағына өлшемнің сезімталдық бірлігінің жартысын қосып-алумен жүзеге асады. Психологиялық айнымалылар кездейсоқ шамалар болып келеді. Себебі олардың қандай мәнге ие болатыны алдын ала белгісіз. Психологиялық зерттеулердегі математикалық өңдеу сыналушылардан кандай да бір белгілері бойынша алынған мәндерімен амалдар жасау. Мұндай индивидуалды нәтижелерді «бақылаулар», «варианттар», индивидуалды көрсеткіштер деп атайды. Психологияда, көбінесе, «бақылау» немесе «бақылау мәндері» деген терминдер қолданылады. Белгінің мәні арнайы өлшем шкалалары арқылы анықталады. Объекттер мен оқиғалаларды белгілі бір ережеге сәйкестіріп, сандық формалар арқылы көрсету өлшем деп аталады. Мәселен, адамның бойын өлшеу оның басынан аяғына дейінгі қашықтықты санмен көрсету. Түрлі құбылыстар мен оқиғалаларды өлшеудің 4 типі болады. Бұлар келесі түрде аталады: 1)номиналды немесе атау шкаласы; 2) ординалды немесе тәртіптік шкала; 3) интервалдар шкаласы; 4) тең қатынастар шкаласы. Атау шкаласы бір объектті екіншісінен ажыратуға мүмкіндік береді. Бұл белгілі бір ортақ, ұқсас белгісі немесе қасыиеті бойынша заттарды немесе объекттерді кластарға біріктіру процессі. Кластарға атаулар беріледі, алайда көбінесе бұл атаулар сандармен көрсетіледі. Атау шкаласының ең қарапайым жағдайы – дихотомиялық шкала – екі-ақ кластан немесе ячейкадан тұрады. Мәселен, жалғыз бала –аға-апалары бар бала, отандас – жат елдік т.б. дихотомиялық шкала бойынша өлшенетін белгі альтернативті деп аталады, оның тек екі-ақ көрсеткіші болады. Атау шкласы үш одан да көп кластардан тұруы мүмкін.мұнда бүкіл объекттерді жіктеп, кластарға бөлген соң, атаулардан сандарға өтуге болады. Атау шкаласы бойынша берілген сандар тек бір кластың екіншісінен өзгеше екендігі туралы ғана мәлімет береді. Мәселен, ағылшындарды – 1, немістерді -2 , қазақтарды – 3деп белгілесек, номиналды немесе атау шкаласы бойынша өлшеу жүргіземіз. Яғни 1 2ден өзгеше, ал 3 1 мен 2ден өзгеше екендігі туралы мәлімет береміз. Бірақ өлшеніп жатқан белгілер үшін сандардың қосындысы немесе тәртіптік қасиеті сәйкес келмейді. 1+2=3 яғни ағылшындар мен немістерді қосқанда қазақтар келіп шығады немесе 1<2<3 яғни ағылшын неміске қарағанда кем, неміс қазаққа қарағанда кем деп айта алмаймыз. Заттардың немесе объекттердің белгілерін немесе қасиеттерін әр түрлі дәрежеде байқасақ,сол заттарды немесе объекттерді тәртіптік өлшеу бойынша сандармен белгілей аламыз. Бұл өлшем «артық-кем» принципі бойынша жүреді. Егер атаулар шкаласында кластар қандай тәртіппен орналасса да болатын болса, мұнда кластардың мәндері ең кішіден ең үлкен мәндерге қарай немесе, керісінше, ең үлкен мәннен ең кіші мәнге қарай тәртіппен орналасады. Тәртіптік шкалада кластардың саны үш кластан көп болу керек. Мәселен, оңды реакция, нейтралды реакция және кері реакция. Сонымен бірге, тәртіптік шкалада өлшенген сандар арқылы тәртіппен орналасқан кластар арасындағы нағыз арақашықтықты білмейміз. Мәселен, «жұмысқа лайықты» және «жұмысқа лайықсыз» деген кластар арасындағы арақашықтық яғни қаншщалықты лайықсыз екендігі белгісіз болады. Бұл шкала бойынша өлшеуді жүзеге асырғанда кластарға рангтар беріп шығамыз. Мәселен, ең төмен көрсеткіштер жиналған класқа 1 ранг, одан жоғарырақ класқа 2 ранг т.с.с. немесе керісінше, ең жоғары мәндер жиналған класқа 1 ранг, одан төменірек бағалар бар класқа 2 ранг т.с.с Тәртіптік шкала бойынша өлшеу белгілі бір мәндердің тәртіптік қатарын береді. Заттар арасындағы тең ара қашықтықты интервалдар шкаласы көрсете алады. Бұл өлшеу «белгілі бір бірлік сандарға көп-белгілі бір бірлік сандарға аз» принципі бойынша жүреді. Белгінің әрбір мәні басқа мәнінен теңдей бірлікте өлшенген ара қашықтықта тұрады. Интервалдық өлшемдер үшін өлшем бірліктері енгізіледі. Градус, сантиметр, грамм – бұлардың барлығы интервалдық шкалаларға мысал бола алады. Тең қатынастар шкаласында объекттер немесе субъекттерді өлшенетін қасиеттердің пропорционалды көріну дәрежесіне байланысты жіктейді. Қатынастар шуаласындағы кластар сандармен белгіленіп, олардың өзара пропорционалдылығы көрсетіледі. Бұл абсолютті нөл нүктесінің болуын болжамдайды. Психологияда тең қатынастар шкаласында өлшенген қасиеттерге мысал ретінде абсолютті сезімталдылық табалдырығы бола алады. Өлшенетін психологиялық айнымалыларды абсолютті нөлге теңестіруді елестету өте қиын. Абсолютті ақымақтық немесе абсолютты шыншыл бұл тұрмыста қолданылатын ұғымдар. Абсолютті нөл объекттер мен субъекттердің санын есептегенде ғана болады. Сөйтіп, көбінесе тең қатынастар шкаласы айнымалылардың жиіліктеріне қатысты ғана қолданылады. Жиілік көрсеткіштеріне қатысты бүкіл арифметикалық операцияларды қолдануға болады. Негізгі әдебиет: 9,10,26. Қосымша әдебиет: 27,12,61. Дәріс 2. СИПАТТАУШЫ СТАТИСТИКА. ҮЛЕСТІРІМ МӘСЕЛЕСІ. Дәріс тезистері. Тәжірибе көрсеткендей, көптеген зерттеу жұмыстарындағы болжамдарды дәлелдеу негізгі үш схема бойынша жүреді. Бірінші схема - өлшеніп жатқан көрсеткіштердің көптеген сандық мәндерін ең негізгі көрсеткіштерге тән мәні бар бірнеше жалпыланған шамалармен ауыстыру және сыналушылардың жекеленген мәндерін топтың берілгендерімен салыстыру. Мұндай жалпыланған шамаларға орталық тенденциялар өлшемі мен өзгергіштік өлшемдері жатады. Орталық тенденциялар ретінде (яғни жан-жағында жекеленген мәндер топтасқан шама) үш түрлі шама қолданылады: орталық арифметикалық, медиана және мода. Ең қарапайым тәсілмен алынатын орталық тенденциялы шама - мода. Мода – көпшілік бақылауда ең жиі кездесетін мән. Мәселен, 36,34,31,31,31,29,23 қатарында мода 31 тең. ( Мо31) Медиананы есептеу үшін көрсеткіштер мәндерінің сандық қатарын алдын ала тәртіпке келтіріп алады. Содан кейін медиананы келесі жолмен анықтауға болады: Қатардағы сандар тақ болса, берілгендердің тәртіптелген қатарында ортадағы орынды алатын санның мәні медиана болады. Мәселен, 36,34,31,29,23 қатарында Md31. Қатардағы сандар жұп болса, берілгендердің тәртіптелген қатарында ортадағы екі орынды алып отырған мәндердің ортасында жатқан нүкте болады. Мәселен, 36,34,31,29 қатарында Md(34+31)/2=32,5 Орталық арифметикалық келесі формуламен есептелінеді: xi і – көрсеткіштің сандық мәні, n – сыналушылар саны. Орталық тендецияның өлшемі ретінде арифметикалық ортаны, моданы немесе медиананы таңдап алу зерттеудің мақсаты мен міндеттеріне байланысты болады, сонымен бірге, зерттеулерде кездесетін берілгендердің сипатына да тәуелді. Мәселен, орталық арифметикалық тек интервалдар және қатынастар шкаласы бойынша жүрген өлшемдер үшін ғана және белгілі бір үлкен, әрі бірыңғай қатарлар үшін ғана есептелінеді. Егер мәндердің саны онша үлкен болмаса және олардың арасында «шектен тыс, ауытқитын » берілгендер болса, онда медиана қолданылады. Мода мен медиана, көбінесе ,тәртіптік шкалалармен өлшенгенде қолданылады. Топ ішіндегі бағалардың варияцияларын сипаттау үшін ауытқу өлшемдері қолданылады. Ауытқу өлшемдеріне стандартты ауытқу мен ауытқу өрісі жатады. Ауытқу өрісі – бұл қатардағы максималды және минималды мәндердің айырмасы. Оның қолайлығы - оңай анықталатындығы. Сонымен бірге ол ең өрескел шама, ол тек шеткі мәндерге ғана сүйенеді де, жоғары тұрақсыздыққа ұшырайды, әсіресе кіші жиындарда. Дисперсия – жиындағы көрсеткіштердің шашыраңқылығын сипаттайтын шама. Дисперсияны бағалау келесі формула бойынша жүреді: Мұндағы, xi - әрбір бақыланатын белгінің мәні; ẍ - белгінің орташа арифметикалық мәні; n – бақылаулар саны. Дисперсияның бағасын квадратты түбірден шығару арқылы стандартты ауытқу немесе орташа квадраттық ауытқу деген шаманы аламыз. Стандартты ауытқу дәлірек ауытқу өлшеміне жатады. Ол келесі формуламен есептелінеді: xi - көрсеткіштің сандық мәндері, n - сыналушылар саны, μ – орталық арифметикалық. Егер қандай да бір себептер орташа мәннен жоғары немесе керісінше, төмен мәндердің жиірек кездесуіне әкелетін болса, онда асимметриялы үлестірім аламыз. Асимметрия келесі формула бойынша есептеледі: 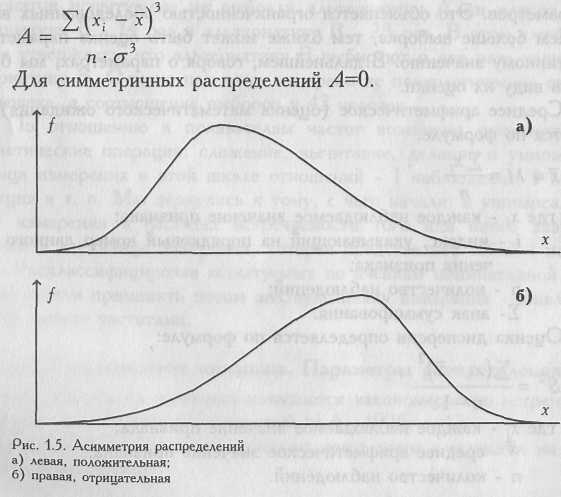 Егер қандай да бір себептердің арқасында көбінесе орташа немесе орташа мәнге жақын мәндер жиі кездесетін болса оңды эксцессті үлестірім аламыз. Егер үлестірімде шеткі мәндер жиі кездесетін болса, және анағұрлым жоғары мен анағұрлым төмен мәндер бір мезгілде жиі кездессе, үлестірім теріс эксцесспен сипатталады. Эксцесстің көрсеткіші мына формула бойынша анықталады: |
