Название понятия (физической величины, закона )
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Раздел физики, изучающий строение и свойства вещества, содержащего огромное количество находящихся в непрерывном хаотическом движении атомов и молекул. Термодинамика — раздел физики, изучающий превращение движения в теплоту и наоборот. | |||
| Предмет и методы исследования | В молекулярной физике разработано два взаимно дополняющих друг друга теоретических метода – статистический и термодинамический. В статистическом методе микроскопические величины, характеризующие движение молекулы (к примеру, ее импульс в данный момент времени), являются непредсказуемыми, случайными. Для построения теории создается гипотетическая модель механизма молекулярного движения и пространственного строения вещества. Затем в этой модели разрабатываются методы нахождения плотности вероятностей тех или иных величин, зная которые вычисляют средние значения этих величин. В термодинамическом методе исследования вещества, в отличие от статистического, не вводятся в рассмотрение какие-либо модельные представления об атомно-молекулярном строении тела, а ставится своей задачей установление зависимости между непосредственно наблюдаемыми макроскопическими (измеряемыми в опыте) величинами, такими как давление, температура, объем, концентрация, напряженность электрического или магнитного поля и т. п. | ||
| Основные положения МКТ | 3 основных положения молекулярно - кинетической теории: 1. Все тела (вещества) состоят из частиц (молекул, атомов, ионов...), между которыми есть промежутки. 2. Частицы находятся в постоянном, беспорядочном (хаотичном) движении (тепловое движение). 3. Частицы вещества взаимодействуют друг с другом: притягиваются на небольших расстояниях и отталкиваются, когда эти расстояния уменьшаются. | ||
| Относительная атомная и молекулярная масса | относи́тельная а́томная ма́сса (устаревшее название — атомный вес) — значение массыатома, выраженное в атомных единицах массы. Определяется как отношение массы атома данного элемента к 1⁄12 массы нейтрального атома изотопа углерода 12C. Из определения следует, что относительная атомная масса является безразмерной величиной Молекулярная масса (менее правильный термин: молекулярный вес) — масса молекулы, выраженная в атомных единицах массы. Численно равна молярной массе, выраженной в г/моль. Однако следует чётко представлять разницу между молярной массой и молекулярной массой, понимая, что они равны лишь численно и различаются по размерности. | ||
| Количество вещества | физическая величина, характеризующая количество однотипных структурных единиц, содержащихся в веществе. Под структурными единицами понимаются любые частицы, из которых состоит вещество (атомы, молекулы, ионы, электроны или любые другие частицы) Единица измерения количества вещества в Международной системе единиц (СИ)-моль | ||
| Молярная масса | Молярная масса вещества (M) – масса одного моля этого вещества. По величине она равна относительной молекулярной массе Mr (для веществ атомного строения – относительной атомной массе Ar). Молярная масса имеет размерность г/моль. | ||
| 17. Опытные законы идеального газа (изопроцессы и их графики). Уравнение состояния идеального газа. | |||
| Идеальный газ | математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что:
| ||
| Закон Бойля-Мариотта | Закон Бойля Мариотта — При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно. Это означает, что с ростом давления на газ его объем уменьшается, и наоборот. Для неизменного количества газа закон Бойля — Мариотта можно также интерпретировать следующим образом: при неизменной температуре произведение давления на объем является величиной постоянной. Закон Бойля — Мариотта выполняется строго для идеального газа и является следствием уравнения Менделеева Клапейрона. Для реальных газов закон Бойля — Мариотта выполняется приближенно. Практически все газы ведут себя как идеальные при не слишком высоких давлениях и не слишком низких температурах. | ||
| Изотермический процесс и его график | При m = const T = const P1V1 = P2V2 или PV = const. Полученное PV = const уравнение называется уравнением изотермического процесса. Это уравнение было получено английским физиком Робертом Бойлем в 1662 году и французским физиком Эдмоном Мариоттом в 1676г. 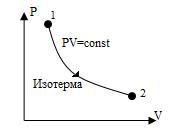 | ||
| Закон Гей-Люссака | Закон Гей Люссака — при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре 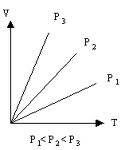 Объем V данной массы газа при постоянном давлении газа прямо пропорционален изменению температуры Закон Гей-Люссака справедлив только для идеальных газов, реальные газы подчиняются ему при температурах и давлениях, далеких от критических значений. Является частным случаем уравнения Клайперона. | ||
| Изобарный процесс и его график | Изобарным процессом называется процесс, протекающий при неизменном давлении(P=const) и условии m = const и М = const. Если в некотором процессе не изменяются масса и давление газа, то уравнение Менделеева-Клапейрона для начального и конечного состояний будет: P1V1 = RT1 и P2V2 = RT2 При m = const P = const V / T = const или V1 / V2 = T1 / T2 (уравнение называется законом Гей-Люссака). Таким же способом, как это было сделано для изохорного процесса, можно получить для изобарного процесса уравнение: Р = соnst. Кривая изобарного процесса называется изобарой. 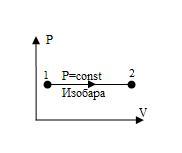 | ||
| Закон Шарля | Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре. В этом и состоит закон Шарля. Из закона Шарля следует, что отношение давлений данной массы газа при постоянном объеме равно отношению его абсолютных температур: | ||
| Изохорный процесс и его график | Изохорным процессом называется процесс, протекающий при постоянном объёме (V = const) и при условии m = const и М = const. При этих условиях из уравнения состояния идеального газа для двух значений температуры Т0 и Т следует: P0V = m RT0 РV = МRT или Р / Р0 = Т / Т0 Для газа данной массы отношение давления к температуре постоянно, если объем газа не меняется. При P1 / P2 = T1 / T2 (это уравнение называется законом Шарля), оно применимо для изохорного процесса: V =const. 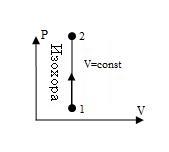 | ||
| Закон Авогадро | физическая величина, численно равная количеству специфицированных структурных единиц (атомов, молекул, ионов, электронов или любых других частиц) в 1 моле вещества. Определяется как количество атомов в 12 граммах (точно) чистого изотопауглерода-12. Обозначается обычно как NA, а иногда и L | ||
| Уравнение Менделеева-Клапейрона | Для этого используют уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева): PV = nRT где n – число молей газа; P – давление газа (например, в атм; V – объем газа (в литрах); T – температура газа (в кельвинах); R – газовая постоянная (0,0821 л·атм/моль·K). | ||
| 18. Основное уравнение МКТ. Средняя кинетическая энергия движения молекул. | |||
| Основное уравнение МКТ | где р - давление газа на стенки сосуда(Па) n - концентрация молекул, т.е. число молекул в единице объема ( 1/м3) - масса молекулы (кг) - средний квадрат скорости молекул ( м2/с2) ρ - плотность газа (кг/м3) - средняя кинетическая энергия молекул (Дж) | ||
| Средняя кинетическая энергия движения молекул | | ||
| 19. Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения. Скорости движения молекул. | |||
| Функция Максвелла для распределения молекул идеального газа по скоростям. График функции распределения Максвелла. | Функция распределения Максвелла где n - общее число молекул в единице объема, т. е. концентрация; dn - число молекул в единице объема, скорости которых лежат в интервале от v до 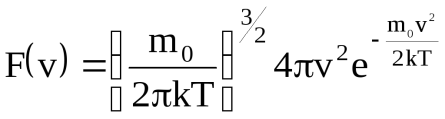 . .График функции распределения Максвелла. 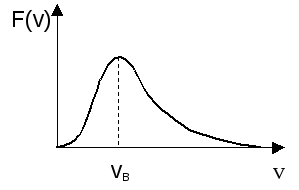 | ||
| Скорости движения молекул: средняя квадратичная, средняя арифметическая и наиболее вероятная скорость движения | Сопоставляя все три скорости: 1) наиболее вероятную 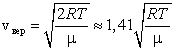 , ,2) среднюю 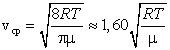 , ,3) среднюю квадратичную 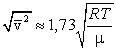 , – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало , – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало | ||
| Распределение молекул по энергиям | Значение законаМаксвелла — Больцмана заключается также в возможности вычисления различных статистических средних свойств молекул — скоростей, энергий. Чем выше температура, тем больше в системе активных молекул, тем выше скорость реакции. | ||
| 20. Барометрическая формула. Распределение Больцмана. | |||
| Барометрическая формула. | Барометрическая формула широко используется для оценки атмосферного давления при различных условиях, хотя она дает слегка завышенные значения. | ||
| Распределение Больцмана | Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового равновесия. Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов. Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P0 в барометрической формуле (2.4.1) на n и n0 и получим распределение Больцмана для молярной массы газа: где n0 и n - число молекул в единичном объёме на высоте h = 0 и h. | ||
| 21. Явления переноса (теплопроводность, диффузия, внутреннее трение). | |||
| Понятие явлений переноса | Явление переноса. В термодинамической неравновесной системе возникают особые неравновесные процессы, называемые явлением переноса., в результате которых происходит перенос в пространстве энергии, массы и импульса. К явлениям переноса относятся: 1) теплопроводность (перенос энергии) ; 2) диффузия (перенос массы) ; 3) внутренние трение или вязкость (перенос импульса) | ||
| Теплопроводность. Закон Фурье. | способность материальных тел к переносу энергии (теплообмену) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Теория теплопроводности рассматривает тело как непрерывную среду. Согласно основному закону теплопроводности - закону Фурье - вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры: где - коэффициент теплопроводности, Вт/(м×К). Он характеризует способность вещества, из которого состоит рассматриваемое тело, проводить теплоту. Знак «-» указывает на противоположное направление вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры. | ||
| Коэффициент теплопроводности. | Коэффициент теплопроводности газов. Согласно кинетической теории перенос теплоты теплопроводностью в газах при обычных давлениях и температурах определяется переносом кинетической энергии молекулярного движения в результате хаотического движения и столкновения отдельных молекул газа. При этом коэффициент теплопроводности определяется соотношением: | ||
| Диффузия | процесс взаимного проникновения молекул или атомов одного вещества между молекулами или атомами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму. | ||
| Закон Фика | Закон Фика первый: плотность диффузионного потока вещества пропорционален градиенту изменения концентрации с коэффициентом пропорциональности D - кэфф. диффузии и направлен в другую от него сторону. Закон Фика второй: скорость изменения плотности диффузионного потока пропорциональна скорости изменения градиента концентрации с тем же коэффициентом D и так же напрвлена в другую сторону. | ||
| Коэффициент диффузии | количественная характеристика скорости диффузии, равная количеству вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1 м²) при градиенте концентрации, равном единице (соответствующем изменению 1 моль/л → 0 моль/л на единицу длины). Коэффициент диффузии определяется свойствами среды и типом диффундирующих частиц | ||
| Внутреннее трение | одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла энергии, затрачиваемой на это перемещение. | ||
| Динамическая вязкость | Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии. В международной системе единиц (СИ), динамическая вязкость измеряется в Паскаль - секундах [Па·с] | ||
| 22. Внутренняя энергия. Работа газа. Первое начало термодинамики. | |||
| Внутренняя энергия | Принятое в физике сплошных сред, термодинамике и статистической физике название для той части полной энергиитермодинамической системы, которая не зависит от выбора системы отсчета | ||
| Внутренняя энергия идеального газа и её расчет | Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома 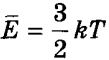 на число атомов на число атомов 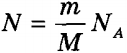 . Учитывая, что k NA = R, получим значение внутренней энергии идеального газа: . Учитывая, что k NA = R, получим значение внутренней энергии идеального газа: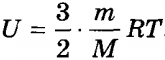 . . | ||
| Работа газа | Формулы для вычисления работы при постоянном давлении: - Работа газа при изобарном процессе (p = const) | ||
| Первое начало термодинамики | Здесь под Первое начало термодинамики (2) является универсальным законом природы. Оно справе-дливо для любых тепловых процессов и любых агрегатных состояний вещества. Ведем еще оду важную физическую величину, необходимую для количественного описания тепловых процессов. | ||
| 23. Теплоемкости. Уравнение Майера. | |||
| Теплоёмкости (C, c, Cµ, CµV, Cµp) | Теплоёмкость (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение количества теплоты (ΔQ), полученного телом, к соответствующему приращению его температуры (ΔT): C = ΔQ/ΔT Единица измерения теплоёмкости в системе СИ — Дж/К. Удельная теплоёмкость — количество теплоты, которое необходимо подвести к телу чтобы изменить его температуру на один градус. Количество вещества может быть измерено в единицах измерения массы, объёма или молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают: массовая теплоёмкость — количество теплоты, которую необходимо подвести к единице массы тела (обычно 1 кг) чтобы нагреть его на 1 K, измеряется в Дж/(кг • К); объёмная теплоёмкость — количество теплоты, которую необходимо подвести к единице объёма вещества (обычно 1 м3) чтобы нагреть его на 1 K, измеряется в Дж/(м3 • К); молярная теплоёмкость — количество теплоты, которую необходимо подвести к 1 молю вещества чтобы нагреть его на 1 K, измеряется в Дж/(моль • К). | ||
| Уравнение Майера | |||
