Название понятия (физической величины, закона )
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
39. Магнитное поле и его характеристики. Магнитное поле Земли. | ||||
| Магнитное поле и его характеристики | Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Количественные характеристики магнитного поля: магнитная индукция В, абсолютная магнитная проницаемость среды μa, Напряженность магнитного поля Н. | |||
| Магнитное поле Земли | Магнитное поле Земли или геомагнитное поле — магнитное поле, генерируемое внутриземными источниками. Предмет изучения геомагнетизма. | |||
| 40. Закон Био-Савара-Лапласа и его применение к расчету полей. | ||||
| Закон Био-Савара-Лапласа и его применение к расчету полей | применение закона Био — Савара — Лапласа совместно с принци пом суперпозиции позволяет довольно просто рассчитать конкретные поля: Магнитное поле прямого тока: 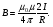 Магнитное поле в центре кругового проводника с током: | |||
| 41. Закон Ампера. Взаимодействие параллельных токов. Сила Лоренца. | ||||
| Закон Ампера | сила, действующая на элемент длины dl проводника с током I, помещенный в магнитное поле с магнитной индукцией В, равна dF = I [dIB]. | |||
| Взаимодействие параллельных токов | Два параллельных тока одинакового направления притягиваются друг к другу с силой, равной 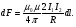 Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания. | |||
| Сила Лоренца | pезультирующая сила, действующая на заряд q, движущийся со скоростью v, со стороны магнитного поля с индукцией Bи электрического поля с напряженностью Е: F=qE+q[vB]. | |||
| 42. Поток вектора магнитной индукции. Теорема Гаусса для потока вектора магнитной индукции. Циркуляция вектора магнитной индукции (закон полного тока). | ||||
| Поток вектора магнитной индукции | Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная 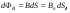 где Bn =В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSп — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. где Bn =В cos a — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSп — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. | |||
| Теорема Гаусса для потока вектора магнитной индукции | Поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: 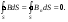 | |||
| Циркуляция вектора магнитной индукции (закон полного тока) | Циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром: где n — число проводников с токами, охватываемых контуром L произвольной формы. | |||
| 43. Магнитные свойства вещества. Диа- и прамагнетики. Ферромагнетизм. | ||||
| Магнитные свойства вещества | Все вещества, помещенные в магнитное поле, намагничиваются и создают собственное магнитное поле, действие которого складывается с действием внешнего магнитного поля: 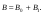 Влияние вещества на внешнее магнитное поле характеризуется величиной 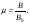 | |||
| Диа- и прамагнетики | Вещества, ослабляющие внешнее магнитное поле, называют диамагнетиками (висмут, азот, гелий, углекислота, вода, серебро, золото, цинк, кадмий и др.). Вещества, усиливающие внешнее магнитное поле, — парамагнетики (алюминий, кислород, платина, медь и др.). | |||
| Ферромагнетизм | Это магнитоупорядоченное состояние вещества, в котором большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной (спонтанной) намагниченностью. | |||
| 44. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца. Самоиндукция. Взаимная индукция. | ||||
| Явление электромагнитной индукции | Явление, при котором в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. | |||
| Закон Фарадея | Э.Д.С. электромагнитной индукции в контуре не зависит от способа изменения магнитного потока и численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: Ei= - dФ/dt | |||
| Правило Ленца | Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток. | |||
| Самоиндукция | Явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции. | |||
| Взаимная индукция | Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. | |||
| 45. Теория Максвелла для электромагнитного поля. Вихревое электрическое поле. Система уравнений Максвелла. | ||||
| Теория Максвелла для электромагнитного поля | Изменяющееся магнитное поле порождает изменяющееся электрическое поле, а переменное электрическое поле порождает переменное магнитное поле. То есть, электрическое и магнитное поля являются составляющими единого электромагнитного поля. И всякое изменение одного из них вызывает появление другого. Эта гипотеза составляет основу теории Максвелла. | |||
| Вихревое электрическое поле | Электрическое поле, созданное переменным магнитным полем, называют вихревым. Вихревое электрическое поле возникает при изменении магнитного поля всегда - независимо от того, есть ли в этом месте пространства замкнутый проводящий контур или нет. Проводящий контур является лишь «индикатором» вихревого электрического поля: оно вызывает в контуре индукционный ток. При перемещении заряда по замкнутому контуру вихревое электрическое поле, в отличие от электростатического поля, совершает над зарядом работу. | |||
| Система уравнений Максвелла | Уравнения Максвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики.  | |||
| 46. Колебательный процесс и его основные характеристики. Гармонические колебания. Маятники. | ||||
| Колебательный процесс и его основные характеристики | Колебательные движения (колебания) – это любые, повторяющиеся через некоторое время движения. Всякое колебание связано с нарушением равновесного состояния системы и выражается в отклонении ее характеристик от равновесных значений. Иными словами, колебанием называется процесс, при котором какая-либо величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около своего среднего значения.В зависимости от физической природы колебания могут быть механи ческие, электромеханические, электромагнитные и др. Механические колебания представляют собой распространяющиеся возмущения упругой среды. К ним относятся колебания маятника, поплавка на воде, изменения плотности и давления воздуха при прохождении звуковых волн и т. п. К электромеханическим колебаниям, возникающим за счет преобразования электрических импульсов в механические, относятся колебания мембраны телефона, пьезоэлемента ультразвуковых преобразователей. Электромагнитные колебания представляют собой распространяющиеся возмущения электромагнитного поля. К ним относятся колебания в электрических контурах, волноводах (радиоволны, свет, рентгеновские лучи). Все колебательные движения, независимо от их природы, имеют общий признак: положение, к которому стремится колеблющееся тело в процессе колебаний. Это - положение устойчивого равновесия.В положении устойчивого равновесия тело может находиться долго, до тех пор, пока внешняя сила не выведет его из равновесия.  | |||
| Гармонические колебания | Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса. Уравнение гармонического колебания устанавливает зависимость координаты тела от времени 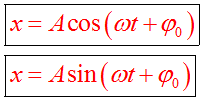 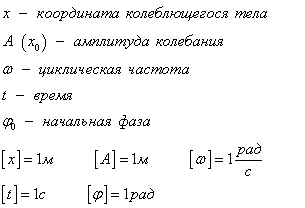 | |||
| Маятники | Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести 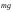 уравновешивается силой натяжения нити уравновешивается силой натяжения нити 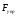 . При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ. Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника. . При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ. Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.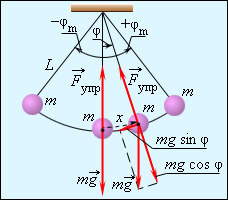 Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим. Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия: 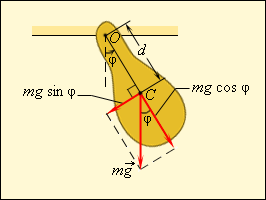
Здесь d – расстояние между осью вращения и центром масс C. Знак «минус» в этой формуле означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания/ | |||
| 47. Механические колебания и их виды колебаний (свободные, затухающие, вынужденные). | ||||
| Механические колебания | Различают следующие виды механических колебаний: –свободные или собственные колебания - происходящие без переменного внешнего воздействия и поступления энергии извне; –периодические - при которых значения обобщенной координаты и ее производных циклически повторяются (если это условие не выполняется, то колебания апериодические); –вынужденные - вызываемые и поддерживаемые переменной во времени внешней силой; –параметрические - вызываемые изменением во времени динамических параметров системы ( жесткости, массы или момента инерции, демпфирования и др.); –автоколебания - стационарные колебания возбуждаемые и поддерживаемые за счет энергии поступающей от источника неколебательного характера, в которой поступление энергии регулируется движением самой системы; – Затухающие колебания — это колебания, амплитуда которых уменьшается с течением времени под действием внешних сил. | |||
