Название понятия (физической величины, закона )
 Скачать 0.91 Mb.
|
Кпд тепловой машины КарноКоличество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно  .Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику  .Отсюда коэффициент полезного действия тепловой машины Карно равен  . | |||
| Теорема Карно | Теорема Карно.1. Из всех тепловых двигателей, работающих при одинаковых условиях, т.е. при одинаковых температурах нагревателей и одинаковых температурах холодильников, максимальным КПД обладает машина, работающая по циклу Карно. 2. КПД машины Карно определяется лишь температурой нагревателя Т1 и температурой холодильника Т2 и не зависит от того, какой газ использован в качестве рабочего тела.  | ||
| 27. Энтропия и её свойства. Третье начало термодинамики (теорема Нернста). | |||
| Энтропия как физическая величина | понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. В статистической физике Энтропия служит мерой вероятности осуществления к--л. макроскопич. состояния, в теории информации-мерой неопределённости к--л. опыта (испытания), к-рый может иметь разл. исходы. Эти трактовки энтропии имеют глубокую внутр. связь. Напр., на основе представлений об информационной энтропии можно вывести все равновесные статистич. распределения (см. Гиббса распределения) Энтропия в термодинамике была введена Р. Клаузиусом (R. Clausius, 1865) на основе второго начала термодинамики, к-рое можно сформулировать математически в виде Клаузиуса неравенства  . Интеграл берётся по замкнутому циклич. процессу, при к-ром система получает (или у неё отбирают) малые количества теплоты dQ при соответствующих значениях абс. температуры Т. | ||
| Свойства энтропии | 1. Энтропия является величиной вещественной и неотрицательной, т.к. значения вероятностей pn находятся в интервале 0-1, значения log pn всегда отрицательны, а значения -pn log pn в (1.4.2) соответственно положительны. 2. Энтропия - величина ограниченная, т.к. при pn 0 значение -pn log pn также стремится к нулю, а при 0 < pn 1 ограниченность суммы всех слагаемых очевидна. 3. Энтропия равна 0, если вероятность одного из состояний источника информации равна 1, и тем самым состояние источника полностью определено (вероятности остальных состояний источника равны нулю, т.к. сумма вероятностей должна быть равна 1). 4. Энтропия максимальна при равной вероятности всех состояний источника информации: Hmax(U) = -  (1/N) log(1/N) = log N.5. Энтропия источника с двумя состояниями u1 и u2 при изменении соотношения их вероятностей p(u1)=p и p(u2)=1-p определяется выражением: 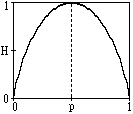 H(U) = -[p log p + (1-p) log(1-p)], и изменяется от 0 до 1, достигая максимума при равенстве вероятностей. График изменения энтропии приведен на рис. 1.4.1. 6. Энтропия объединенных статистически независимых источников информации равна сумме их энтропий. Рассмотрим это свойство на двух источниках информации u и v. При объединении источников получаем обобщенный источник информации (u,v), который описывается вероятностями p(unvm) всех возможных комбинаций состояний unисточника u и vm источника v. Энтропия объединенного источника при N возможных состояниях источника u и М возможных состояниях источника v: H(UV) = - p(unvm) log p(unvm),Источники статистически независимы друг от друга, если выполняется условие: p(unvm) = p(un) p(vm). С использованием этого условия соответственно имеем: H(UV) = - p(un)p(vm) log [p(un)p(vm)] == - p(un) log p(un)p(vm) -p(vm) log p(vm)p(um).С учетом того, что p(un) = 1 иp(vm) = 1, получаем:H(UV) = H(U) + H(V). (1.4.3) 7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля, полностью игнорируя содержательную сторону ансамбля. С одной стороны, это расширяет возможности использования энтропии при анализе самых различных явлений, но, с другой стороны, требует определенной дополнительной оценки возникающих ситуаций. Как это следует из рис. 1.4.1, энтропия состояний может быть неоднозначной, и если в каком-либо экономическом начинании действие u с вероятностью pu=p приводит к успеху, а действие v с вероятностью pv=1-p к банкротству, то выбор действий по оценке энтропии может оказаться и прямо противоположным, т.к. энтропия при pv=p равна энтропии при pu=p. | ||
| Теорема Нернста | содержание тепловой теоремы Нернста сводится к двум утверждениям. Первое утверждение состоит в том, что при приближении к абсолютному нулю энтропия стремится к определённому конечному пределу. Поэтому имеет смысл говорить об энтропии тела при абсолютном нуле температур. То есть интеграл 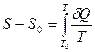 сходится. Вторая часть теоремы Нернста утверждает, что все процессы при абсолютном нуле температур, переводящие систему из одного равновесного состояния в другое равновесное состояние, происходят без изменения энтропии. | ||
| 28. Реальный газ. Уравнение Ван-дер-Ваальса. Изотермы реальных газов. | |||
| Понятие реального газа | газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева | ||
| Уравнение Ван-дер-Ваальса | Уравнение состояния реального газа:  где а, в – постоянные величины для различных газов. | ||
| Изотермы реальных газов | Изотермы Ван-дер-Ваальса — кривые зависимости р от Vmпри заданных T, определяемые уравнением Ван-дер-Ваальса для молягаза. При высоких температурах (Т > Тkизотерма реального газа отличается от изотермы идеального таза только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Tк на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической, соответствующая ей температура Tk — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем Кк и давление ркназываются также критическими. Состояние с критическими параметрами (pk, Vk, Tk) называется критическим состоянием. При низких температурах (Т Рассматривая различные участки изотермы при Т < Тк, видим, что на участках 1—3 и 5—7 при уменьшении объема Vm давление р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1, Часть 6—7 отвечает газообразному состоянию, а часть 2—1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.  | ||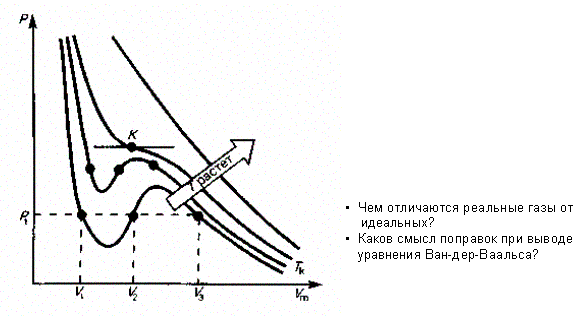
| 29. Внутренняя энергия реального газа. Эффект Джоуля-Томпсона. Сжижение газов. | |||
| Внутренняя энергия реального газа |  где Uμ - внутренняя энергия киломоля газа в Дж/кмоль, i - число степеней свободы движения молекулы газа. | ||
| Эффект Джоуля-Томпсона | При адиабатическом расширении газа без совершения им полезной работы температура газа изменяется. | ||
| Сжижение газов | переход вещества из газообразного состояния в жидкое. Оно достигается охлаждением их ниже критической температуры (Тк ) и последующей конденсацией в результате отвода теплоты парообразования (конденсации). | ||
| 30. Жидкости: строение и свойства. Поверхностное натяжение. Смачивание. Капиллярные явления. | |||
| Жидкости: строение и свойства | Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может переместиться в соседнее вакантное место. Поэтому молекулы не привязаны к определенным центрам и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах. | ||
| Поверхностное натяжение | Поверхностное натяжение – основная термодинамическая характеристика поверхностного слоя жидкости на границе с газовой фазой или другой жидкостью. Поверхностное натяжение различных жидкостей на границе с собственным паром изменяется в широких пределах: от единиц для сжиженных низкокипящих газов до нескольких тысяч мН/м для расплавленных тугоплавких веществ. Поверхностное натяжение зависит от температуры. Для многих однокомпонентных неассоциированных жидкостей (вода, расплавы солей, жидкие металлы) вдали от критической температуры хорошо выполняется линейная зависимость:  | ||
| Смачивание | процесс самопроизвольный, который сопровождается уменьшением запаса свободной поверхностной энергии. Отсюда следует, что из двух жидкостей лучше смачивает данную поверхность та , при растекании которой поверхностная энергия системы уменьшается на большую величину | ||
| Капиллярные явления | Капиллярное давление. Так как силы поверхностного (межфазного) натяжения направлены по касательной к поверхности жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина которого Dp связана со средним радиусом кривизны поверхности r0 уравнением Лапласа: Dp = p1 - p2 = 2s12/r0 где p1 и p2- давления в жидкости 1 и соседней фазе 2 (газе или жидкости), s12 - поверхностное (межфазное) натяжение | ||
| 31. Твердые тела: строение и свойства. Фазовые переходы. | |||
| Кристаллы и аморфные твердые тела (строения и свойства, виды кристаллов). | Аморфные телапо своей внутренней структуре очень напоминают жидкости, поэтому их часто называют переохлаждёнными жидкостям. Как и жидкости, аморфные тела структурно изотропны. Их свойства не зависят от рассматриваемого направления. Объясняется это тем, что в аморфных телах, так же, как и в жидкостях сохраняется ближний порядок (координационное число), а дальний (длины и углы связей) отсутствует.Этими обеспечивается полная однородность всех макрофизических свойств аморфного тела. Типичными примерами аморфных тел являются стекла, смолы, битумы, янтарь. Кристаллические тела, в отличие от аморфных, имеют четкую упорядоченную микроструктуру, которая сохраняется на макроуровне и проявляется внешне в виде мелких зерен с плоскими гранями и острыми ребрами, называемых кристаллами. Распространенные в природе кристаллические тела (металлы и сплавы, сахар и поваренная соль, лед и песок, камень и глина, цемент и керамика, полупроводники и т д) обычно являются поликристаллами,состоящими из хаотично ориентированных, сросшихся между собой монокристалликов (кристаллитов),размеры которых составляют около 1 мкм (10-6 м) Однако иногда встречаются монокристаллы достаточно больших размеров. Например, монокристаллы горного хрусталя достигают человеческого роста В современной технике монокристаллы играют важную роль, поэтому разработана технология их искусственного выращивания. Внутри монокристалла атомы (ионы) вещества размещаются с соблюдением дальнего порядка, в узлах четко ориентированной в пространстве геометрической структуры, получившей название кристаллической решёткиКаждое вещество образует в твердом состоянии свою, индивидуальную по геометрии кристаллическую решётку. Ее форма определяется структурой молекул вещества. В решетке всегда может быть выделена элементарная ячейка,сохраняющая все её геометрические особенности, но включающая в себя минимально возможное число узлов. | ||