Название понятия (физической величины, закона )

Название	Название понятия (физической величины, закона )
Дата	17.03.2018
Размер	0.91 Mb.
Формат файла
Имя файла	-1604870888.docx
Тип	Документы #38670
страница	2 из 9

1 2 3 4 5 6 7 8 9

Полное ускорение при криволинейном движении

при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Направление полного ускорения

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой: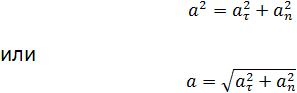

img-pkhvrz

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

_τ +

Единицы измерения ускорения

В системе СИ: м/с²

4. Кинематика вращательного движения твердого тела.

Угловое перемещение и его направление

векторная величина, характеризующая изменение угловой координаты в процессе её движения.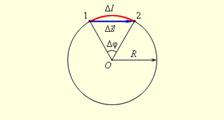

Направление углового перемещения

совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.

Угловая скорость и её направление

называется векторная величина, равная первой производной угла поворота тела по времени:

Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с).

Линейная скорость точки

Угловое ускорение и его направление

называется векторная величина, равная первой производной yгловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω ), при замедленном - противонаправлен ему

Единицы измерения угловых кинематических величин

В системе СИ:

Угловое перемещение: [φ] = рад

Угловая скорость: [w]= рад/с;

Угловое ускорение: [Ɛ]= рад/с²

Частота вращения

физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. Рассчитывается, как отношение количества повторений или возникновения событий (процессов) к промежутку времени, за которое они совершены. Стандартные обозначения в формулах — ν, f или F.

Формула частота вращения тела; число оборотов в единицу времени.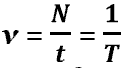

vr6

В системе СИ: ГЦ=1/с

Период вращения

время, за которое тело совершает полный оборот вокруг оси или полюса (точки).

В Си период измеряется в секундах (c)

Связь линейных и угловых величин

отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от угловой скорости ω и расстояния r соответствующей точки до оси вращения. Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ. Поделим обе части равенства на

Переходя к пределам при , получим

или .

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. По определению ускорения, или

что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси вращения. Формула устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу.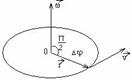

5. Законы Ньютона.

Первый закон Ньютона

всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.

Инерция

свойство тел оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствие или при взаимной компенсации внешних воздействий

ИСО- Инерциальные системы отсчета

это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно) , как и система, связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы

Сила

векторная физическая величина, являющаяся мерой воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений. В системе СИ:F=H

Масса

Скалярная неотрицательная релятивистски инвариантная физическая величина, одна из важнейших величин в физике. В нерелятивистском приближении, когда скорости тел много меньше скорости света, определяет их инерционные и гравитационные свойства

В системе СИ:m=кг

Инертность

Импульс тел

векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

$\large p=m\upsilon$

Второй закон Ньютона (две формулировки)

1)Ускорение, приобретаемое материальной точкой в инерциальной системе отсчета:
- прямо пропорционально действующей на точку (равнодействующей) силе;
- обратно пропорционально массе точки; и
- направлено в сторону действия силы.

F=ma

2) Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.

Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.

Производную в формуле можно заменить на отношение конечных приращений:

Третий закон Ньютона

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

6. Силы в механике. Сила трения (покоя, скольжения, качения). Деформации. Силы упругости.

Сила трения (покоя скольжения, качения)

Взаимодействие, которое возникает в месте соприкосновения двух тел и препятствует их относительному движению, называют трением. А силу, которая характеризует это взаимодействие, называют силой трения.

Сила трения покоя препятствует твёрдым телам приходить в движение. Она направлена всегда против направления «сдвигающей» силы.

Если тело скользит по какой-либо поверхности, его движению препятствует сила трения с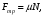кольжения:

, где N — сила реакции опоры, a μ — коэффициент трения скольжения.

Сила трения качения — сила сопротивлению движения, возникающее при перекатывании тел друг по другу.

Деформации

Это изменение формы и размеров твердых тел под действием внешних сил.

Относительная деформация

Относительными называют деформации определяемые отношением изменения размера (абсолютной деформации) к соответствующим начальным размерам тела.

Другими словами относительные деформации показывают насколько изменился размер тела в сравнении с его размерами до нагружения.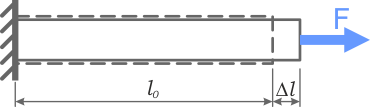

определение относительной продольной деформации

определение относительной продольной деформации

Например, при растяжении (сжатии) прямого стержня его относительное удлинение ε находится отношением абсолютного удлинения Δl к начальной длине l₀.

Абсолютная деформация

Абсолютными называют деформации определяемые величиной изменения соответствующего размера либо положения сечения.

Нагляднее всего абсолютную деформацию можно показать на примере растяжения-сжатия.

Рассмотрим прямой стержень, длину которого до нагружения обозначим как l₀.

начальная длина стержня до нагружения

После приложения к стержню продольной растягивающей силы F его длина увеличится до некоторого значения l₁.

длина бруса после растяжения

Разность между конечным и начальным продольными размерами стержня есть его абсолютная деформация при растяжении.

Единица измерения абсолютных деформаций:

линейные – метр [м] или миллиметр [мм],
угловые – радиан [рад] или градусы [^o].

Механическое напряжение

это мера внутренних сил, возникающих в деформируемом теле под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.
s равно отношению модуля силы упругости F_упр к площади поперечного сечения тела S:

Модуль упругости(модуль Юнга)

E — характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к удлинению. Часто модуль Юнга называют просто модулем упругости.

Сила упругости и закон Гука (две формулировки)

1)Сила упругости, возникающая при деформации тела, прямо пропорциональна величине деформации и направлена в сторону, противоположную перемещению частиц.

F= — kx

2) Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

7. Силы тяготения. Сила тяжести. Гравитационное поле Земли. Аномалии ускорения свободного падения.

Силы тяготения

Силами тяготения называют результат гравитационных взаимодействий, которые описываются законом всемирного тяготения, открытым Ньютоном: материальные точки притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними:

Сила тяжести

Сила тяжести направлена к центру Земли и на поверхности Земли равна:

F = mg

Гравитационное поле Земли

Под гравитационным полем Земли понимается поле силы тяжести (точнее, ускорения силы тяжести), которая определяется как равнодействующая двух основных сил: силы притяжения (тяготения) Земли и центробежной силы, вызванной ее суточным вращением.

Аномалии ускорения свободного падения

Экспериментально установлено, что ускорение свободного падения не зависит от массы падающего тела, но зависит от географической широты

местности и высоты h подъема над земной поверхностью. При этом зависимость g от

двоякая. Во-первых, Земля – не шар, а эллипсоид вращения, то есть радиус Земли на полюсе меньше радиуса Земли на экваторе. Поэтому сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе (g = 9,832 м/с² на полюсе и g = 9, 780 м/с² на экваторе).
Во-вторых, Земля вращается вокруг своей оси и это влияет на ускорение свободного падения, приводя к его зависимости от географической широты местности. Установлено, что на географической широте 45⁰ у поверхности Земли ускорение свободного падения равно 9,80665 м/с² (округленно 9,81 м/с²).
Земля не является однородным шаром. там, где плотность земного вещества больше, больше сила притяжения и больше ускорение свободного падения.

8. Импульс тела и системы тел. Закон сохранения импульса. Центр масс.

Импульс тела и системы тел

Импульсом тела называется величина, равная произведению массы тела на его скорость. Импульс имеет такое же направление, как и скорость. Для замкнутой системы тел выполняется закон сохранения импульса: в замкнутой системе векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия.

Закон сохранения импульса

Векторная сумма импульсов всех тел замкнутой системы – величина постоянная, если внешние силы, действующие на неё, отсутствуют, или же их векторная сумма равна нулю. Закон сохранения импульса называют также законом сохранения количества движения.

Центр масс

Центр масс является точкой приложения вектора импульса системы , так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:

где - масса и радиус-вектор каждой частицы системы, M - масса всей системы.

9. Работа силы. Мощность.

Работа постоянной силы

Работа постоянной силы.

Работой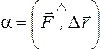

постоянной силы называется скалярное произведение вектора силы

и вектора перемещения

; где

.

Работа – скаляр.

Если на тело действует несколько сил (N – число сил), и вектор перемещения тела равен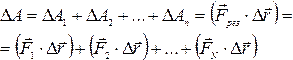

, то совершаемая работа равна алгебраической сумме работ, совершаемых каждой из действующих на тело сил на этом перемещении.

img-jrxpir

Определение знака работы силы

Знак работы определяется знаком косинуса угла между силой и перемещением. Если

, то

, так как косинус острых углов положителен. При

работа отрицательна, так как косинус тупых углов отрицателен. При

(сила перпендикулярна перемещению) работа не совершается.

Расчет работы переменной силы

Работа переменной силы.

Если рассматриваемый участок траектории разбивается на большое число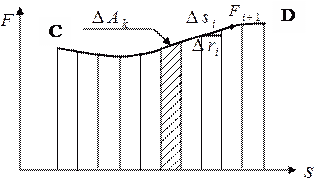

элементарных участков, то длина пути элементарного участка будет близка к величине перемещения на этом участке

. Путь ограничен точками С и D (рисунок 1.2.1.). img-gfyynw

Рисунок 1.2.1. – Зависимость переменной силы от пути

При бесконечно большом количестве участков, на которое разбивается путь (

), приращения величин перейдут в бесконечно малые величины

, а работа переменной силы на участке пути

выражается криволинейным интегралом:

, где

. Если силу разложить на касательную и нормальную составляющие, то работу составляет только

– касательная составляющая силы, направленная по касательной в каждой точке траектории.

Силы, работа которых по замкнутому контуру равна нулю, называются потенциальными. В механике к потенциальным силам относятся сила тяжести и сила упругости.

Консервативная сила

называются сила, работа которой не зависит от пути перемещения, а определяется только начальной и конечной конфигурациями системы.

Мощность

физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Единицы измерения работы и мощности

Работа:в системе СИ-Дж(Джоуль)

Мощность: в системе СИ измеряется в ваттах (Вт) Один ватт (1 Вт) — это такая мощность, при которой за 1 ссовершается работа 1 Дж: 1 Вт = 1 Дж/с.

10. Кинетическая и потенциальная энергия. Примеры расчета потенциальной энергии. Закон сохранения механической энергии.

Кинетическая энергия и её расчет.

энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

— масса тела

— скорость центра масс тела

— момент инерции тела

— угловая скорость тела.

Теорема об изменении кинетической энергии

изменение кинетической энергии механической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении:

Потенциальная энергия

энергия взаимодействия тел. Потенциальной энергией тело само по себе не может обладать. Потенциальная энергия определяется силой, действующей на тело со стороны другого тела. Поскольку взаимодействующие тела равноправны, то потенциальной энергией обладают только взаимодействующие тела.

Физическую величину, равную половине произведения жесткости тела на квадрат его деформации, называют потенциальной энергией упругодеформированного тела: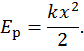

потенциальная энергия

Примеры расчета потенциальной энергии

Потенциальная энергия сжатой пружины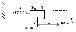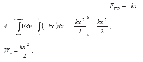

Если между телами системы действуют консервативные силы, то такая система обладает потенциальной энергией, причём её численное значение будет равно работе консервативных сил по переводу системы из данной конфигурации к конфигурации с условно нулевым уровнем потенциальной энергии.

Закон сохранения механической энергии

Если работа внешних неконсервативных сил и работа внутренних неконсервативных сил равна нулю, а внешние потенциальные поля стационарны, то механическая энергия системы остаётся постоянной: W = W_p + W_k = const.

11. Момент инерции. Момент силы. Основной закон динамики вращательного движения.

Момент инерции

физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Момент силы

Моментом силы относительно неподвижной точки O называется псевдовекторная величина равная векторному произведению радиус-вектора , проведенному из точки O в точку приложения силы, на силу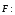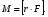

Модуль момента силы:

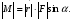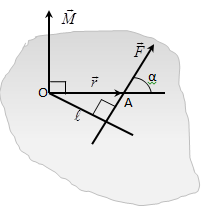http://bog5.in.ua/lection/mechanics_lect/image_mech/lect8_meh_clip_image013.png

Основной закон динамики вращательного движения

Момент силы равен произведению момента инерции на угловое ускорение: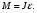

12. Момент импульса. Закон сохранения момента импульса.

Момент импульса

Моментом импульса материальной точки относительно неподвижной точки () называется физическая величина, определяемая векторным произведением:

,

Моментом импульса относительно неподвижной оси (z) называется скалярная величина (), равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки (О) данной оси. Момент импульса () не зависит от положения точки О на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Закон сохранения момента импульса

Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия

$\large m_1\upsilon_1+m_2\upsilon _2=m_1\upsilon _1^l +m_2\upsilon _2^l$

$\large p_1+p_2=p_1^l +p_2^l$

13. Условия равновесия твердого тела. Виды равновесия.

Условия равновесия твердого тела

Необходимым и достаточными условиями равновесия свободного твердого тела является равенство нулю векторной суммы всех внешних сил, действующих на тело, равенство нулю суммы всех моментов внешних сил относительно произвольной оси, равенство нулю начальной скорости поступательного движения тела и условие равенства нулю начальной угловой скорости вращения

Виды равновесия

1) устойчивое (при изменении силы тело возвращается к положению равновесия, W_п = min);

2) неустойчивое (при изменении силы тело далеко уходит от положения равновесия, W_п = max);3) безразличное(смещение тела не нарушает его равновесия, W_п = const)W_п- потенциальная энергия

14. Давление в жидкости и газе. Закон Паскаля. Закон Архимеда. Уравнение неразрывности. Уравнение Бернулли и следствия из него.

Давление в жидкости и газе

Физическая величина, определяемая нормальной силой, действующей со стороны жидкости (или газа) на единицу площади, называется давлением p жидкости (или газа): p=ΔF/ΔS.

Закон Паскаля

Производимое внешними силами давление в какое-то место жидкости или газа, передается по жидкости или газу без изменения в любую точку.

Закон Архимеда

На всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.

Уравнение неразрывности

Соотношение вида S₁V₁=S₂V₂=const, означающее, что произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока, есть величина постоянная для данной трубки тока. Уравнение неразрывности потока демонстрирует закон сохранения массы: количество втекающей и вытекающей жидкости неизменно.

Уравнение Бернулли и следствия из него

При стационарном течении идеальной жидкости полное давление, равное сумме статического, динамического и гидростатического давлений, одинаково во всех поперечных сечениях трубки тока.

ρυ²/2 + ρgh + p = const

Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.

Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда.

15. Вязкость (внутреннее трение). Режимы течения жидкостей.

Вязкость (внутреннее трение)

одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла.

Сила вязкого трения F, действующая на жидкость, пропорциональна (в простейшем случае сдвигового течения вдоль плоской стенки) скорости относительного движения v тел и площади S и обратно пропорциональна расстоянию между плоскостями h.

Режимы течения жидкостей

Ламинарным называется сложное течение без перемешивания частиц жидкости и без пульсаций скоростей и давлений. При ламинарном движении жидкости в прямой трубе постоянного поперечного сечения все линии тока направлены параллельно оси труб, отсутствуют поперечные перемещения жидкости. Однако, ламинарное движение нельзя считать безвихревым, так как в нем хотя и нет видимых вихрей, но одновременно с поступательным движением имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров с некоторыми угловыми скоростями.

Турбулентным называется течение, cопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении наряду с основным продольным перемещением жидкости происходят поперечные перемещения и вращательное движение отдельных объемов жидкости.

16. Молекулярная физика и термодинамика. Предмет и методы исследования. Основные положения МКТ. Относительная атомная и молекулярная масса, количество вещества, молярная масса.

Молекулярная физика и термодинамика