Название понятия (физической величины, закона )
|
Определение (формулировка закона) или формула
|
1.Предмет и структура, основные понятия и характеристики механики.
|
Кинематика
|
часть теоретической механики, в которой изучаются движения материальных тел без учета их масс и действующих на них сил
|
Динамика
|
раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия
|
Статика
|
называется раздел механики, изучающий условия равновесия тел
|
Классическая механика
|
это раздел классической физики, изучающий механическое движение макроскопических объектов, которые движутся со скоростями много меньше скорости света ( =3 108 м/с). Под макроскопическими объектами понимаются объекты, размеры которых м. (размер типичной молекулы).
|
Релятивистская механика.
|
(эйнштейновская) механика изучает движение материальных объектов при скоростях, сравнимых со скоростью света в вакууме.
|
Квантовая механика
|
раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка.
|
Механическим движение
|
называют измене�ние положения тела в пространстве относительно других тел с течением времени. Например, человек, едущий на эскалато�ре в метро, находится в покое относительно самого эскалатора и перемещается относительно стен тунне�ля
|
Виды механического движения
|
прямолинейные и криволинейные — по форме траектории;
равномерные и неравномерные — по закону движения.
|
Материальная точка
|
тело, размерами и формой которого можно пренебречь в данных условиях движения, считая массу тела сосредоточенной в данной точке. Модель материальной точки – простейшая модель движения тела в физике. Тело можно считать материальной точкой, когда его размеры много меньше характерных расстояний в задаче.
|
Абсолютно твёрдое тело (твёрдое тело)
|
тело, расстояние между частями которого не изменяется при действии на него сил, т.е. форма и размеры твёрдого тела не меняются при действии на его любых сил. Конечно таких тел в природе не существует. Это физическая модель. В тех случаях, когда деформации алы, можно реальные тела рассматривать как абсолютно твёрдые. Движение твердого тела в общем случае очень сложно.
|
Система отсчета
|
это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которой рассматривается движение каких-либо тел
|
Радиус-вектор
|
обычно обозначается
{\displaystyle {\vec {r}}} или просто {\displaystyle \mathbf {r} }r) — вектор, задающий положения точки в пространстве (например, евклидовом) относительно некоторой заранее фиксированной точки, называемой началом координат.
|
Кинематические уравнения движения
|
При движении материальной точки М ее координаты и радиус-вектор изменяются с течением времени t.
Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
либо зависимость от времени радиус-вектора этой точки
Три скалярных уравнения (1.2) или эквивалентное им одно векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки.
|
Траектория
|
непрерывная линия, вдоль которой движется материальная точка в заданной системе отсчета. В зависимости от формы траектории различают прямолинейное и криволинейное движение материальной точки.
|
→
Перемещение (S)
{\displaystyle {\vec {S}}}
|
Вектор(s), соединяющий начальную и конечную точки движения.
Проекция вектора перемещения на данную ось: sx = x - x0.
Формулы перемещения:
Перемещение при равномерном движении.
Перемещение при равноускоренном движении
.
Другие формулы, где встречается перемещение: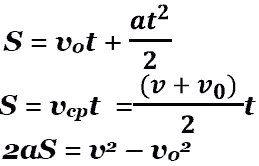
Скорость при равномерном движении.
Работа силы

Перемещение - векторная величина
|
Путь (s)
|
это длина траектории. То есть длина той, возможно, кривой линии, по которой двигалось тело. Путь скалярная величина
В СИ единица измерения пути −− метр: [L]=м[L]=м.
Путь всегда больше или равен модулю перемещения. Путь не может быть отрицательным.
|
2. Скорость движения
|
→
Скорость (v)
|
векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.
формула зависит от вида движения:
равноускоренное движение то v=v0+at
равномерное движение то s=vt, где v=s/t.
Единицы измерения: СИ-м/с
|
Средняя скорость
|
в кинематике, некоторая усреднённая характеристика скорости движущегося тела (или материальной точки). Различают два основных определения средней скорости, соответствующие рассмотрению скорости как скалярной либо векторной величины: средняя путевая скорость (скалярная величина) и средняя скорость по перемещению (векторная величина). При отсутствии дополнительных уточнений, под средней скоростью обычно понимают среднюю путевую скорость.
|
Средняя (путевая) скорость
|
— это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:
Формула:
|
Мгновенная скорость
|
это скорость тела в данный момент времени или в данной точке траектории. Это векторная физическая величина, численно равная пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени:
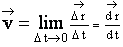
|
Вектор скорости в декартовой системе координат (ДСК)
|
Вектором средней скорости точки в интервале времени от t до t+Δt называют отношение приращения радиуса-вектора точки за этот промежуток времени к его величине :
Вектор средней скорости направлен также, как вектор перемещения т.е. вдоль хорды МN.
|
Модуль скорости
|
это число, которое показывает, насколько быстро тело передвигается в пространстве.
|
Направление скорости
|
так же как направление физически малого вектора перемещения, определяется по чертежу траектории
|
Единицы измерения скорости.
|
В системе СИ: м/с
|
3. Ускорение и его составляющие.
|
Ускорение
|
это физическая величина (a, от лат. acceleratio), характеризующая быстроту изменения скорости тела. Ускорение является векторной величиной, показывающей, насколько изменяется вектор скорости  тела при его движении за единицу времени: тела при его движении за единицу времени:
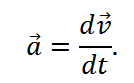
|
Среднее ускорение
|
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
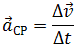
где 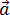 – вектор ускорения. – вектор ускорения.
|
Мгновенное ускорение
|
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
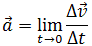
|
Вектор ускорения в ДСК
|
В декартовой системе вектор положения задается в виде 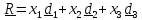 , где- координаты вектора, а , где- координаты вектора, а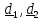 ,– ортонормированный базис, т.е. базисные векторы единичные и взаимно-перпендикулярные. В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами: ,– ортонормированный базис, т.е. базисные векторы единичные и взаимно-перпендикулярные. В этом случае координаты равны проекциям вектора на оси, задаваемые базисными векторами: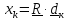 . .
Векторы скорости и ускорения равны
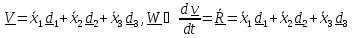 , ,
а их модули 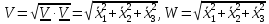
|
Модуль ускорения
|
ускорение является вектором, то есть учитывает не только изменение величины скорости (модуля векторной величины), но и изменение её направления. В частности, ускорение тела, движущегося по окружности с постоянной по модулю скоростью, не равно нулю; тело испытывает постоянное по модулю (и переменное по направлению) ускорение, направленное к центру окружности (центростремительное ускорение).
|
Тангенциальное (касательное) ускорение
|
это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
|
Нормальное ускорение
|
это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 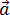 n. Вектор нормального ускорения направлен по радиусу кривизны траектории. n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
|
| |
 Скачать 0.91 Mb.
Скачать 0.91 Mb.