Астрономия шпоры. Небесная сфера. Отвесная линия. Ось мира. Меридиан наблюдателя. Система сферических координат и полярных координат
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
Нутация. Изменение сил притяжения за счет изменения расстояний и направлений между Землей, Солнцем и Луной вызывают более быстрые колебания оси Земли называемых нутацией (рис. 20). Нутацией называется периодическое изменение координат светил вследствие изменения положения оси Земли в пространстве под воздействием переменной части сил притяжения. Период наибольшего колебания равен 18,6 года, что указывает на его связь с Луной. Координаты всех светил изменяются за счет нутации (нут и нут) на величину до 0,3. Годичная аберрация. Годовое движение Земли вызывает смещение луча света от светила в направлении движения Земли, которое называется годичной аберрацией. Годичной аберрацией называется смещение луча света от светила за счет годового орбитального движения Земли. Причиной возникновения явления годичной аберрации (рис. 21) является сопоставимость орбитальной скорости Земли Vз = 30 км/с со скоростью света С = 3105 км/с.
где u – угол наклона телескопа к направлению движения Земли. Так как угол у мал, то sin y = у arc 1 и он определится формулой где k = 20,5 – постоянная аберрации. По величине урассчитываются поправки координат абер и абер светил за годичную аберрацию. Изменение экваториальных координат звезд. Видимые координаты звезд в и в непрерывно изменяются по следующим причинам:
В результате точных обсерваторных наблюдений рассчитываются средние координаты светил 0, 0 и их годовые изменения за счет собственного движения (, ), которые помещаются в звездные каталоги на начальный момент – эпоху, например начало 2000 г. Видимые координаты звезд на момент наблюдений рассчитываются по формулам :  (32) в= 0+(пр+ ) t + нут+ абер; в= 0+(пр+ ) t + нут+ абер. где t – число лет в тропических годах от начальной эпохи. После учета прецессии и собственного движения получим средние места звезд на момент наблюдений. После учета действия нутации получим истинные координаты и после учета поправки за аберрацию – видимые координаты звезд. Таким методом предвычисляются координаты звезд на несколько лет вперед, которые приводятся в астрономических ежегодниках. 17. МАЕ. Расчет координат светил. Судового времени. Явлений Солнца и Луны. Схемы В России выпускаются следующие ежегодники:
В морском астрономическом ежегоднике по формулам небесной механики на заданные (табличные) моменты гринвичского времени предвычислены координаты светил, время явлений (кульминаций, восхода, захода и т.п.) и другие астрономические данные. Содержание МАЕ состоит из двух частей:
Основные данные помещены в ежедневных таблицах МАЕ. На каждом развернутом листе приведены данные для трех суток: на левой странице – гринвичские часовые углы точки Овна (звездное время –Sгр), гринвичские часовые углы и склонения Солнца, Венеры, Марса, Юпитера, Сатурна и Луны; внизу левой страницы – время верхней кульминации, прямое восхождение и параллакс планет. На правой странице – гринвичские часовые углы и склонения Луны, местное время восхода и захода Солнца и Луны, начало и конец сумерек на среднюю дату листа, азимуты восхода и захода Солнца, внизу страницы – время кульминаций, радиусы Солнца и Луны др. В настоящее время в большинстве развитых стран, включая Россию, форма официальных морских ежегодников стандартная. Из иностранных ежегодников назовем совместный англо–американский «The Nautical Almanac», немецкий «Nautisches Jahrbuch». Кроме официальных ежегодников за рубежом выпускаются ежегодники–справочники, например – «Brown’s Nautical Almanac». Таблицы МАЕ для расчета координат светил В ежедневных таблицах на каждом развернутом листе приведены данные для трех суток. Аргументом для расчета координат светил является гринвичское время (дата и Тгр), которое задано с интервалом 1ч. Для Солнца, Луны и планет даны табличные гринвичские координаты часовых углов (tт) и склонений (т) на каждый целый час. Кроме этого, даны табличные гринвичские часовые углы точки Овна (tгр= Sгр= Sт) для расчета часовых углов звезд. Расчет звездного времени. Связь между звездным временем и средним солнечным временем рассмотрена в разделе. Используя формулу (37) для Гринвичского меридиана, получим формулу, по которой рассчитываются табличные значения (на каждый целый час) точки Овна в ежедневных таблицах МАЕ. tгр= Sгр= Sт = Тгр 12ч + Ä (44) Формулу расчета звездного времени (S) за избыток Т сверх целого часа получим дифференцированием формулы(44) по Т: и переходя к конечным приращениям В скобках Т = 1ч = 60м = 900. Так как Ä= 59,14 за сутки, то где – коэффициент перевода среднего времени в звездное. S = T +T (45) Рассчитанные по формуле (45) поправки на каждую минуту и секунду часа приведены в «Основных интерполяционных таблицах» (ОИТ) в колонке «Точка Овна». Расчет местного звездного времени выполняется по формуле Sм = Sт + S c (46) Расчет часовых углов и склонений звезд. Из основной формулы времени (34) получим формулу расчета часового угла звезд t = Sм – * = Sм + *, где * = 360° – * – звездное дополнение. Используя формулу (46), получим t = Sт + S c + * (47) Координаты * и * для 160 звезд, в порядке возрастания их , приведены в разделе МАЕ «Звезды. Видимые места», для которых необходимо выполнить интерполяцию на число в месяце. Кроме этого в ежедневных таблицах приведены координаты 66 наиболее ярких звезд, не требующих процедуры интерполяции. Расчет часовых углов и склонений Солнца, планет и Луны. Из основной формулы времени (33) известно, что в один и тот же момент имеет место равенство t  гр + Ä = tсвгр + св гр + Ä = tсвгр + свили t  свгр = tгр + Ä – св свгр = tгр + Ä – свИспользуя формулу (35) для нахождения св, получим формулу расчета через интервал 1ч табличных значений часовых углов Солнца, Луны и 4-х планет tсвгр = Тгр 12ч + Ä – св (48) По этой формуле рассчитаны табличные значения часовых углов Солнца, планет и Луны с интервалом 1ч ежедневных таблиц МАЕ. Примечание. Координаты св и на заданный момент рассчитываются по формулам небесной механики. Вывод формулы расчета приращения часового угла. Продифференцируем формулу (48) по Т и перейдя к конечным приращением, получим 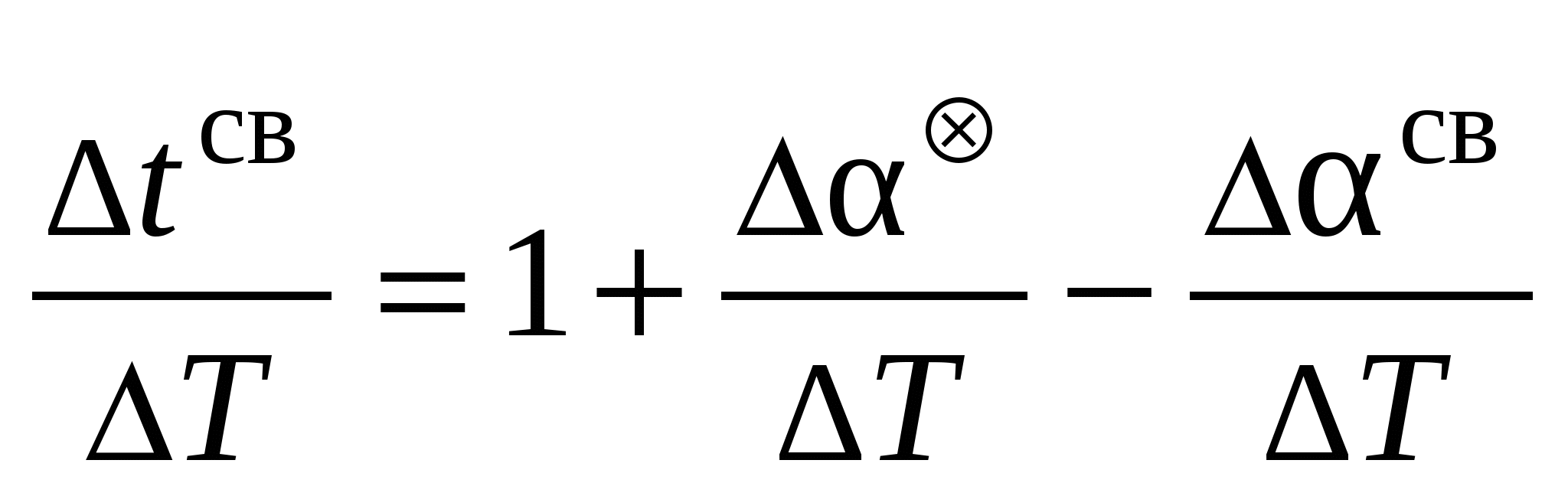 . .Принимая изменение прямых восхождений за Т = 1ч = 60м = 900 и прибавив и отняв постоянную величину  (49) (49)Поправка 1t – равномерная часть изменения св , а поправка за квазиразность 2t – учитывает неравномерность изменения св. К 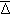 вазиразностью ( ) называется разность между наибольшим изменением светила за 1ч и действительным изменением его за данный час. вазиразностью ( ) называется разность между наибольшим изменением светила за 1ч и действительным изменением его за данный час.Часовые изменения склонения Солнца, планет и Луны () одного порядка с квазиразностями. З 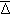 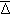 начения и для Солнца и планет на среднюю дату ежедневных таблиц МАЕ (одни на 3 дня) приводится под колонкой tгр и соответственно, а для Луны – на каждый час. Их необходимо интерполировать на данную минуту. В ОИТ в двух крайних колонках приведены часовые изменения / и пропорциональные им значения на данную минуту. начения и для Солнца и планет на среднюю дату ежедневных таблиц МАЕ (одни на 3 дня) приводится под колонкой tгр и соответственно, а для Луны – на каждый час. Их необходимо интерполировать на данную минуту. В ОИТ в двух крайних колонках приведены часовые изменения / и пропорциональные им значения на данную минуту.Учитывая вышеизложенное, получим расчетные формулы местного часового угла и склонения по МАЕ: t  (50) свм = tт + 1t + 2t c св = т + Определение времени кульминации «через часовой угол».Эта задача решается переводом местного часового угла явления (0° или 180°) в гринвичский угол светила и входя в МАЕ обратным ходом по tсвгр определяем Т и затем Т. Определение времени видимого восхода (захода) Солнца, Луны и времени сумерек При движении по суточной параллели Солнце (рис. 30) проходит утром и вечером ряд характерных положений (явлений) имеющих собственные названия. Видимым восходом Твосх. (заходом Тзах.) Солнца называется момент появления (исчезновения) верхнего края Солнца относительно видимого горизонта. Сумерками называется явление постепенного возрастания освещенности утром и убывания вечером.
Гражданскими сумерками называется промежуток времени от захода Солнца до снижения его центра на высоту h= –6° (утром наоборот). Конец гражданских сумерек (Тк.гр.сум.) характеризуется хорошей видимости горизонта, возможностью читать и появлением ярких звезд, высота которых больше 60° – 70°. Навигационными сумерками называется промежуток времени изменения высоты Солнца от h= – 6° до h= – 12° (утром наоборот). Конец навигационных сумерек (Тк.н.сум.) характеризуется видимостью всех звезд, а горизонт уже не виден. Наилучшим временем наблюдением звезд секстаном является промежуток времени изменения высоты Солнца от h= – 2,5° до h= – 9° вечером. и утром на наоборот. Обоснование расчета времени явлений Солнца и Луны в МАЕ. Время явлений зависит от высоты светил в момент конкретного явления, широты места () и долготы (для МАЕ гр= 0°) наблюдателя.
Высоту Солнца в момент восхода (захода) получим по формуле h= – d– +p – R, (55) где d– наклонение видимого горизонта; – астрономическая рефракция; р – параллакс Солнца; R – видимый радиус Солнца. Для расчета моментов восхода и захода Солнца приняты следующие значения: d = 0; + p = – 34,3; R = = – 16, т.е. h = – 50,3. Для гражданских сумерек h = – 6° и навигационных h = – 12°. Для восхода и захода Луны: + p = + 22,7; R= – 15,5;.h= + 7,2. Из параллактического треугольника по данным , иhяв получим sinh = sinφ sin + cosφ cos costм откуда С учетом уравнения времени формула (36) и формулы связи часового угла Солнца со временем (35) получим время явления Т явм = tявм + η 12ч, (57) где tявм – часовой местный угол явления истинного Солнца для м = 0°; Т явм – среднее солнечное время явления. Время явлений Луны и планет с учетом основной формулы времени определяется по следующей формуле Т явм = tявм +(св – ) + η 12ч (58) Практические формулы расчета времени восхода (захода) Луны по МАЕ. Для Луны время явления меняется очень заметно. Поэтому его необходимо обязательно интерполировать по широте и долготе (Т) и расчет выполняется по формуле Тявс = Тявт + Т + Т Правила интерполяции по долготе полностью совпадают с правилами, которые рассмотрены в разд. 1.6.3 Практические формулы расчета времени явлений Солнца по МАЕ. Местное время восхода (захода) Солнца и начала (конца) навигационных (гражданских) сумерек на Гринвичском меридиане (Тявт) дается только на среднюю дату листа ежедневных таблиц МАЕ и для фиксированной табличной широты. Для получения времени явления на заданную дату (Тявм) и широту места (м) следует рассчитать и учесть суточное изменение (с), а также выполнить интерполяцию по широте (Т) и долготе места (Т) Тявм = Тявт + с + Т + Т (59) Примечание. На практике обычно поправку Т не учитывают, так как в широтах до 50° она равна 0м. В широтах более 50°, как правило, наблюдается аномальное состояние атмосферы, при котором Тявт не соответствует действительному. Переход к судовому времени выполняется по формуле Тявс = Тявм Явления, помеченные в МАЕ знаками ///, соответствуют полярной ночи, полярному дню и сумеркам всю ночь. Время начала наблюдений звезд вечером определяется как середина гражданских сумерек, а утром как середина навигационных сумерек. Так как этому времени не предъявляется большая точность, то расчет продолжительности сумерек выполняется по данным на среднюю дату и ближайшую к заданной табличную широту. Для вечерних наблюдений начало гражданских сумерек совпадает со временем захода Солнца и расчет выполняется по формуле  (61) (61)где Начало утренних наблюдений расчет выполняется по формуле  (62) (62)где 19. Звездный глобус. Опознание светил.Нанесение планет и снятие координат. Звездный глобус. Звездный глобус (рис. 33) предназначен для приближенного решения задач мореходной астрономии.
После установки звездного глобуса по широте наблюдателя и местному звездному времени наблюдений меридиональное кольцо соответствует меридиану наблюдателя. В рабочем состоянии звездный глобус находится в горизонтальном кольце ящика, являющегося истинным горизонтом (7), на котором нанесена градуировка координаты азимута в круговом счете и наименование основных направлений – N, E, S, W. На кольце истинного горизонта установлена подвижная крестовина вертикалов (8), на которых нанесена градуировка координаты высоты. Верхняя точка крестовины (пересечение вертикалов) соответствует точке зенита наблюдателя (6). На глобусе двойными линиями нанесены следующие основные круги небесной сферы: небесный экватор (2), эклиптика (9) и меридианы точек равноденствий и солнцестояний. Шкала небесного экватора оцифрована в градусной мере через 10° и во временной мере от точки Овна (на глобусе 360°). Отсчет на экваторе у меридионального кольца в качестве меридиана светила является прямым восхождением светила , а отсчет в качестве меридиана наблюдателя является местным звездным временем Sм. Боковая шкала меридионального кольца предназначена для установки звездного глобуса по широте места наблюдателя и оцифрована в градусах от 0° на полюсах мира до 90° на небесном экваторе. Шкала на верхней поверхности меридионального кольца является шкалой координаты склонения () планет, Луны и Солнца и ограничена величиной 30°. Кроме того, на глобус нанесена сетка небесных меридианов (3) через 15° и небесных параллелей (5) через 10°, а также места 167 звезд, отмеченные греческими буквами и русскими названиями созвездий. Расположение и конфигурация созвездий на звездном глобусе является зеркальным по отношению к картине наблюдаемой с Земли, т.е. наблюдатель находится в центре звездного глобуса. Поэтому при изучении и ориентировки наблюдаемого звездного неба используют карты звездного неба, которые прилагаются в каждом МАЕ, а не звездный глобус. Решение задач на звездном глобусе. С помощью звездного глобуса решают следующие основные задачи:
Примечание. При решении задач на глобусе используются горизонтная (h и А) и 2–я экваториальная ( и ) система координат, т. е. часовые углы светил не используются. Опознаватель звезд «STAR FINDER 2102-D» Вместо звездных глобусов за рубежом широко применяются опознаватели звезд например «Star Finder 2102-D». 21. Основные теории секстана. Выверки. Опр. Поправки индекса. Теоретические основы секстана Секстаном называется угломерный инструмент, построенный на принципе отражательной системы и предназначенный для измерения углов на подвижном основании.
Отражательная система секстана состоит из 2–х зеркал А и В, плоскости которых перпендикулярны плоскости рисунка:
– угол падения (отражения) луча светила (объекта) на большом зеркале В. – угол падения (отражения) отраженного луча от большого зеркала В на малое зеркало А. Измерение угла достигается путем поворота зеркала В до совмещения дважды отраженный луч от объекта З (светило) с прямовидимым лучом от объекта Г (горизонт). Установим зависимость между измеряемым углом h и углом образованным пересечением плоскостей зеркал . Поправка места нуля. Действительное место нуля секстана практически не совпадает с нуль-пунктом лимба вследствие нарушения правильного положения малого и большого зеркал при работе с секстаном.
Поправкой места нуляi0 называется разность между нуль-пунктом 0° (360°) и отсчетом места действи-тельного нуля на лимбе М0. iо = 0°(360°) – Mo (71) Например, на рис. 38 поправка положительная (+ io). Так как при измерении углов отсчет на лимбе секстана (ОС – отсчет секстана) снимается относительно 0°, то действительный угол получим после исправления его поправкой iо, т. е. h = OC + iо. (72) Поправка за параллакс зеркал. В навигации секстан используется для измерений горизонтальных и вертикальных углов относительно земных ориентиров или измерений высоты светила относительно земного объекта (например, берега или ватерлинии другого судна перекрывающих горизонт под светилом). Так как расстояние между центрами зеркал А и В по вертикали (сторона ВЕ рис. 38) приблизительно равна 5 см., то лучи ПВ и ПА не параллельны и образуют угол у. Параллаксом зеркал называется угол, под которым видны зеркала А и В со стороны ориентиров. При совмещении прямовидимого луча П1 с отраженным от зеркала В лучом П2 (линия П1П2 в окуляре трубы рис. 38) получим начальный отсчет на лимбе Мo (линия ВМo). Линии Г1 прямовидимый (слева) и Г2 отраженный (справа) горизонты. Угол между ними равен у. Величина угла у зависит от расстояния ПЕ. Определим расстояние, при котором у < 0,1. Из ПВЕ имеем tgy = BE / ГЕ, (73) принимая tgy = у arc 1 получим Следовательно, при расстоянии более 1 мили у = 0. Поправка индекса секстана. Отсчет на лимбе секстана при совмещении прямовидимого и отраженного изображений объекта называется отсчетом индекса Oi. Поправкой индекса секстанai называется алгебраическая разность между нуль-пунктом 0°(360°) и отсчетом индекса секстана. i = 0°(360°) – Oi (75) Поправка индекса может быть со знаком «+» или «–» и равна сумме поправки места нуля лимба (io) и параллакса зеркал (у). Выверка секстана. При измерении углов в отсчетах секстана (ОС) имеются погрешности, как в отсчете любого механического измерительного прибора. Эти погрешности для секстана возникают из-за нарушения параллельности визирной оси дневной трубы плоскости лимба, перпендикулярности плоскости большого и малого зеркал к плоскости лимба, т. е. параллельность плоскостей зеркал в положении алидады 0°. Процесс регулировки секстана с целью уменьшения этих ошибок называется выверкой секстана. В комплект секстана входят два диоптра и регулировочный ключ, предназначенные для выполнения выверки секстана. Выверка секстана выполняется в следующей последовательности:
Выверка параллельности оси дневной трубы плоскости лимба. Приблизительная оценка параллельности (проверка необходимости выполнения выверки) выполняется секстаном с дневной трубой и алидадой установленной на отсчет более 30°, причем трубу секстана следует направить ниже горизонта. Выверка перпендикулярности большого зеркала к плоскости лимба. Эта выверка выполняется в помещении. Секстан без трубы устанавливается горизонтально на ящик секстана. Алидаду поставить на отсчет около 40° и откинуть светофильтры большого зеркала. Выверка перпендикулярности малого зеркала плоскости лимба методом параллельности плоскостей зеркал. Эта выверка выполняется с дневной трубой секстана ночью по неяркой звезде, находящейся на небольшой высоте, а днем по Солнцу. Уменьшение поправки индекса секстана. Уменьшение поправки индекса секстана выполняется путем изменения положения малого зеркала с помощью его регулировочного винта 3 рис. 42. Она может выполняться по горизонту, звезде или Солнцу так же, как выверка параллельности малого зеркала большому зеркалу. Отличие состоит в том, что отраженное и прямовидимое светило совмещается при помощи регулировочного винта по вертикали.
Алидаду секстана, приготовленного для наблюдений Солнца, устанавливают около 0° (между отсчетом 0° и 359°). После наведения трубы на Солнце отраженное изображение С1 будет находиться над прямовидимым изображением С. Вращая отсчетный барабан, совместить край отраженного изображения С1 с краем прямовидимого С (рис. 47 положение С1) и снять первый отсчет секстана Оi1 (359°--,-‘). Затем перевести отраженное изображение С1 через прямовидимое в положение С2 и снять отсчет секстана Оi2 (0°--,-′=360°--,-′). Средний отсчет Оiср соответствует отсчету совмещения центров прямовидимого и отраженного изображений Солнца, а поправку индекса получим по формуле Оценка точности наблюдений основана на сравнении действительного радиуса Солнца (RМАЕ), который находим в МАЕ на дату наблюдений, с радиусом, полученным из наблюдений (Rизм). По рис. 47 видно, что разность отсчетов индексов равна 4Rизм = Оi2 – Оi1. (80) Расхождение 4Rизм с 4RМАЕ должно быть не более ±0,4. Расхождение больше +0,4 означает, что край отраженного Солнца не совмещен (не доведен) с краем прямовидимого Солнца, а расхождение меньше –0,4 означает перекрытие краев отраженного и прямовидимого Солнца. Точность поправки индекса по Солнцу 0,1 обеспечивается при осреднении 3-х значений i. 22,23. Испр. Высот, приведение высот к одному месту. Необходимость исправления высот. Любое определение места судна выполняется по измеренным навигационным параметрам. В мореходной астрономии измеряемым навигационным параметром является высота светила, которая измеряется секстаном, как угол между видимым положением светила и видимым горизонтом (рис. 48, hизм). В результате измерения с секстана снимается отсчет секстана (ОС). После исправления его поправкой индекса (i) получим измеренную высоту светила hизм. в топоцентрической системе координат, начало которой находится в точке М на высоте над уровнем моря е (глаз наблюдателя). Поправка высоты за астрономическую рефракцию. Явление преломления луча от светила в земной атмосфере называется астрономической рефракцией. Поправка высоты за суточный параллакс. Угол р, под которым из центра светила виден радиус Земли для данного места наблюдателя называется суточным параллаксом светила. Другими словами, это угол (дуга) между видимым (топоцентрическим) и истинным (геоцентрическим) местом светила Суточный параллакс возникает у светил, расстояние до которых сопоставимо с радиусом Земли.  Рис. 49 Из рисунка видно что параллакс р меняется в зависимости от высоты светила. Наибольшей величины ро он достигает при h=0° и называется горизонтальным параллаксом. Для наблюдателя на экваторе Rз наибольший и параллакс называется горизонтальным экваториальным параллаксом. Этот параллакс приводится в МАЕ для светил солнечной системы Луны до 61,5, Венеры до 33, Марса до 24 и Солнца 8,8. Поправка высоты за видимый радиус для Солнца и Луны. Измерение высот Солнца и Луны выполняется путем совмещения верхнего или нижнего края светила с видимым горизонтом. Видимым радиусом светила называется угол, под которым радиус светила виден с Земли. Это топоцентрический радиус. В МАЕ приведены геоцентрические радиусы Солнца и Луны. Для Солнца разность этих радиусов мала и она не учитывается. Для Луны она достигает 0,26 и учитывается в таблицах исправления высот Луны. Земная рефракция. Явление преломления луча света от земных объектов в атмосфере называется земной рефракцией. Земная рефракция характеризуется углом r между истинным и видимым направлением на удаленный земной объект Наклонение видимого горизонта. Видимый горизонт представляет малый круг на поверхности моря, описанный лучом зрения АаВ (рис. 51) наблюдателя А с высоты над уровнем моря е. Наклонением видимого горизонта d называется вертикальный угол HAB между истинным и видимым горизонтом. Наклонение зрительного луча. Если высота светила измерена над объектом, перекрывающим видимый горизонт, например береговой чертой (на рис. 51 точка П) или ватерлинией другого судна, то вместо наклонения горизонта используется наклонение зрительного луча dп. hв = hизм – dп (90) Величина dп выбирают из соответствующей таблицы МТ-2000 по высоте глаза наблюдателя и расстояния до объекта. Общая формула исправления высот. Высоты светил измеренных над видимым горизонтом исправляются поправками, приведенных в формулах (78), (79), (83), (85), (86), (89). С учетом всех поправок, получим общую формулу исправления высот: ho = OC + i + (–d) + (–h) + hp + ht + hВ R (91) После ввода поправки индекса и наклонения горизонта получим «видимую высоту» hв, которая является аргументом для получения остальных поправок. Исправление высот звезд и планет. Так как для звезд и планет Юпитер и Сатурн R = 0 и hp = 0, то получим следующую формулу ho = OC + i + (–d) + (–h) +ht + hВ (92) Для ближайших к Земле планет Венеры и Марса еще добавляется поправка за параллакс hp. Исправление высот Солнца. Исправление высот выполняется по формуле (89), но так как для Солнца ро = 0,15, то объединив поправки –h и hp в общую поправку h+р = (–h) + hp получим формулу ho = OC + i + (–d) + (–h+р) + ht + hВ R (93) Исправление высот Луны. Величина видимого углового радиуса и параллакса Луны зависят от расстояния между Землей и Луной, которое непрерывно изменяется. Поэтому радиус получают через параллакс и исправление высот выполняется общими поправками по аргументам hв и ро, выбранного из МАЕ на момент наблюдений (Тобгр). ho = OC + i + (–d) + ОП +ДП + ht + hВ, (94) где ОП – основная поправка (учет средних значений ро R и (–h); ДП – дополнительная поправка (учет отклонений pо, R и края Луны. 2.5.4. Приведение высот к одному месту (зениту) и одному моменту Измерение высот светил и обработка наблюдений осложняется тем, что высоты и азимуты изменяются вследствие суточного вращения Земли, т. е. по времени, и движения судна, т. е. изменение координат места. Учет изменения высот за счет движения судна называется приведением высот к одному месту (зениту). Учет изменения высот по времени за счет суточного вращения Земли называется приведением высот к одному моменту. Приведение высот светил к одному месту (зениту). Для определения места по светилам необходимо измерить высоты не менее 2-х светил, причем измерения должны быть выполнены относительно одного места судна (с, с). При движении судна измерения высот выполняется из разных мест на Земле (процесс измерения высоты 1-го светила занимает 4 и более минут), вследствие чего высоты светил в один и тот же момент будут разные. Для получения высот как бы измеренных из одной точки (с, с) необходимо выполнить операцию приведения высот к одному месту (зениту) аналитическим или графическим способом.
В момент Т1 и относительно зенита (места) наблюдателя Z1 измерена высота h1 светила С. Азимут на светило в круговом счете А1. Так как судно движется со скоростью Vуз и курсом ПУ(К), то в момент Т2 (измерение высоты другого светила) зенит (место) наблюдателя будет Z2, а высота светила, которую бы измеряли в момент Т1 равна h2. Изменение высоты h1 от перемещения судна равно (90°– h1) – (90°– h2) = h2 – h1 = hz, откуда h2 = h1 + hz (95) Для определения величины hz опустив сферический перпендикуляр Z 2D на вертикал Z1Cиз точки Z2, получим сферический треугольник Z1Z2D, в котором Z1Z2 = S; q = A1 – ПУ; Z1D hz. Принимая Z1Z2D за плоский, получим расчетную формулу поправки hz hz = S cos(A1 – ПУ) = S cos q. (95) Так как S = VT, то из формулы (95) получим расчетную формулу где Т = Тобгр – Тгрi – промежуток времени в минутах между моментом наблюдения i-го светила и моментом обсервации места (снятия с, с); Ai – счислимый азимут (относительно с, с) i-го светила. Знак поправок hz зависит от знаков сомножителей Т и cos qi. Формула (96) является приближенной, так как А1 А2 и сферический треугольник Z1Z2D принят за плоский прямоугольный. Поэтому погрешность в hz будет меньше 0,1 при плавни до 10 15 миль. Графический способ приведения высот светил к одному месту (зениту) рассмотрен в [1]. Приведение высот светил к одному моменту. Высоты приводятся к одному моменту при расчете средней квадратической погрешности (СКП) измерений высоты mос и при предвычислении линии положения. Вывод формулы расчета поправки высоты к намеченному моменту и ее анализ приведен в разделе 1.3.2. В практических расчетах используют формулу в виде ht = 0,25 cos sin A Tc, (97) где А – азимут светила в круговом счете на момент приведения Тпр; Tc = Tпр – Tизм – разность в секундах между моментом приведения и моментом измерения высоты. Формула (95) является приближенной, поэтому применять ее можно только до Tc 180с. |








